转体拱桥混凝土球铰设计参数优化研究

杨 鹏

中国铁建昆仑投资集团有限公司, 四川 成都 610000

0 引言

我国拟建或在建的跨径为80～150 m的大跨径转体拱桥,通常采用混凝土球铰进行转体施工,而有关球铰的设计参数取值依靠工程经验。球铰作为转体施工的核心构件,其设计参数对于球铰结构接触应力的分布具有十分重要的影响[1-2]。

球铰结构的接触应力计算属于复杂的高度非线性问题,通常采用计算精度高、速度快的数值仿真方法。姚国文 等[3]结合钢构拱桥放张式竖转施工技术特点,采用有限元法详细分析了接触位置转动铰结构的整体受力情况;赵云安 等[4]分析了某预应力混凝土T形刚构桥转体结构的局部应力分布,指出转体结构局部会出现应力集中的现象,需要增加补强措施来保证转体施工的安全稳定;张琪峰[5]将混凝土的抗拉强度标准值作为确定支承半径的依据,得出了不同吨位下球铰的合理支承半径以及曲率半径;白文阳[6]通过有限元数值模拟分析了球铰支座的变形及受力特性,可为同类型转体桥梁的设计和施工提供借鉴;何圣杰[7]考虑转动角速度、墩高、不平衡力矩作用等因素与风荷载的耦合作用对转体施工稳定性的影响。由此可见,有关球铰设计参数对结构接触应力变化的系统性研究鲜有报道,这严重制约了混凝土球铰的进一步推广和应用。

鉴于此,本文以黄梅龙坪拱桥为研究对象,建立混凝土球铰结构局部精细化有限元模型,探究曲率半径、支承半径以及下球铰露出高度等参数对球铰接触应力的影响,并基于响应面法对其影响性进行量化评价,以期为混凝土球铰的设计优化提供一定的参考。

1 有限元数值模型

本文依托工程设计图,采用有限元软件ABAQUS建立球铰结构精细化三维数值模型(见图1)。数值模型共分为5个部分,分别为磨盖、磨心、倒圆锥台体、下承台、定位钢轴,模型共有38 352个单元,均为六面体C3D8R实体单元。需要特别说明的是,上、下球铰之间的接触采用面-面接触,通过有限元软件中的罚函数定义切向行为,接触面上的法向行为定义为硬接触,接触面摩擦系数为0.05,边界约束设置为约束下承台底面位移。

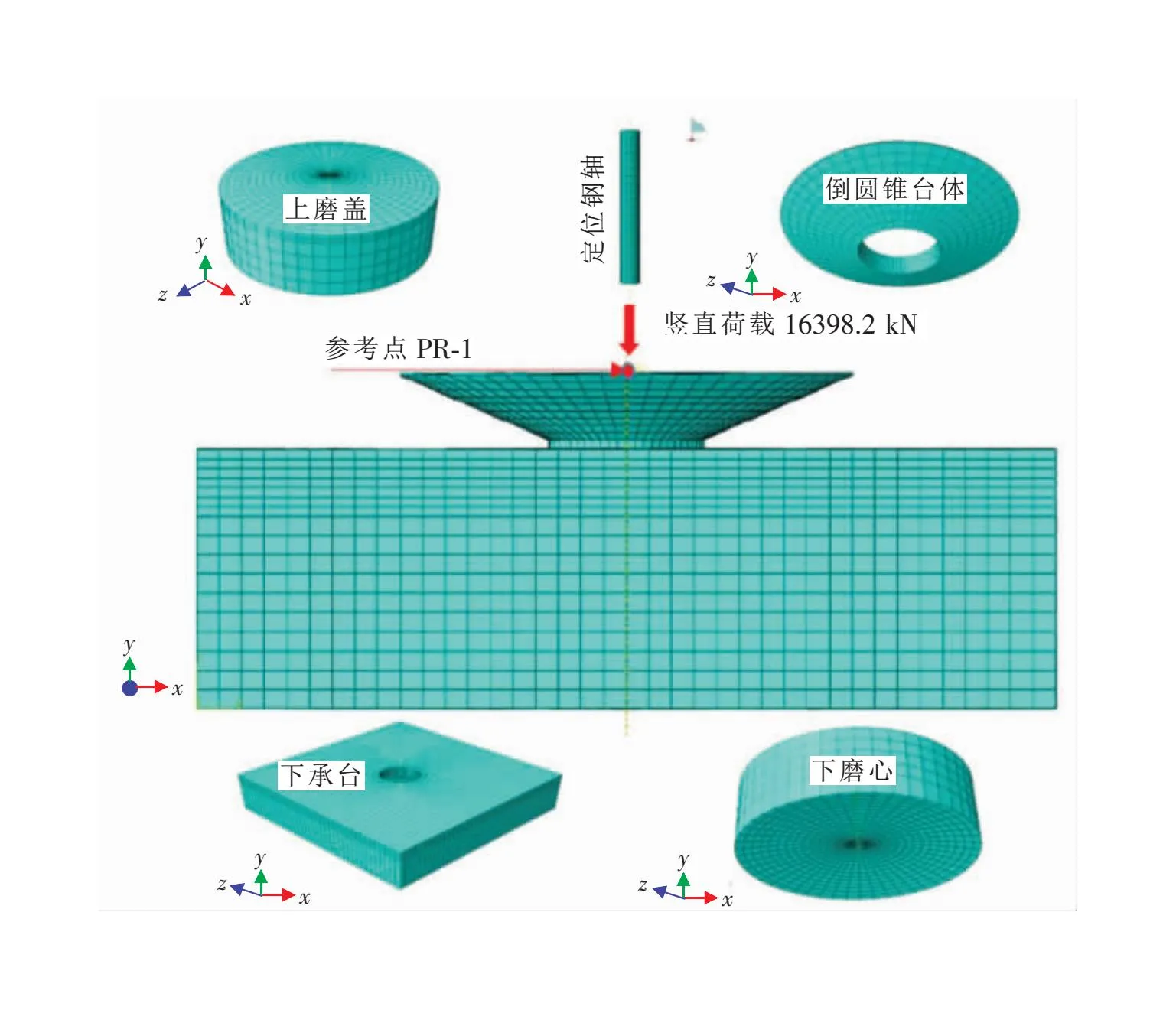
图1 精细化有限元数值模型

上锥体表面耦合于参考点PR-1上,并施加16 398.2 kN的上部构造荷载,下承台、倒锥体采用C30混凝土,磨心、磨盘采用C40混凝土,定位钢柱采用Q235型钢材,材料详细计算参数如表1所示。

表1 材料计算参数

为研究混凝土球铰曲率半径(Rs)、球铰支承半径(Rf)以及下磨心露出高度(Hi)等设计参数对于球铰结构接触应力的影响,采用控制变量法设置以下分析工况。

1)支承半径(Rf)为1.0 m,下磨心露出高度(Hi)为0.1 m,曲率半径(Rs)参数的取值分别为4.0、4.5、5.0、5.5、6.0、8.0、10.0 m以及无穷大。

2)曲率半径(Rs)为5.0 m,下磨心露出高度(Hi)为0.1 m,支承半径(Rf)参数的取值为0.7、0.85、1.0、1.25、1.5和2.0 m。

3)曲率半径(Rs)为5.0 m,支承半径(Rf)为1.0 m,下磨心露出高度(Hi)为0、0.05、0.1、0.15、0.20、0.30 m。

2 数值计算结果分析

2.1 曲率半径对球铰接触应力的影响

不同曲率半径下球铰的接触应力如图2所示,可以看出:曲率半径(Rs)对球铰接触应力的大小和分布形式均具有显著的影响。当Rs为4.0 m时,球铰最大接触应力为5.58 MPa,当Rs为无穷大时,球铰最大接触应力为6.72 MPa。从接触应力分布形式来看,曲率半径(Rs)越小,球铰界面上的接触应力分布越均匀;反之,曲率半径(Rs)越大,球铰界面上的接触应力分布越不均匀,尤其是球铰边缘位置的接触应力最大。

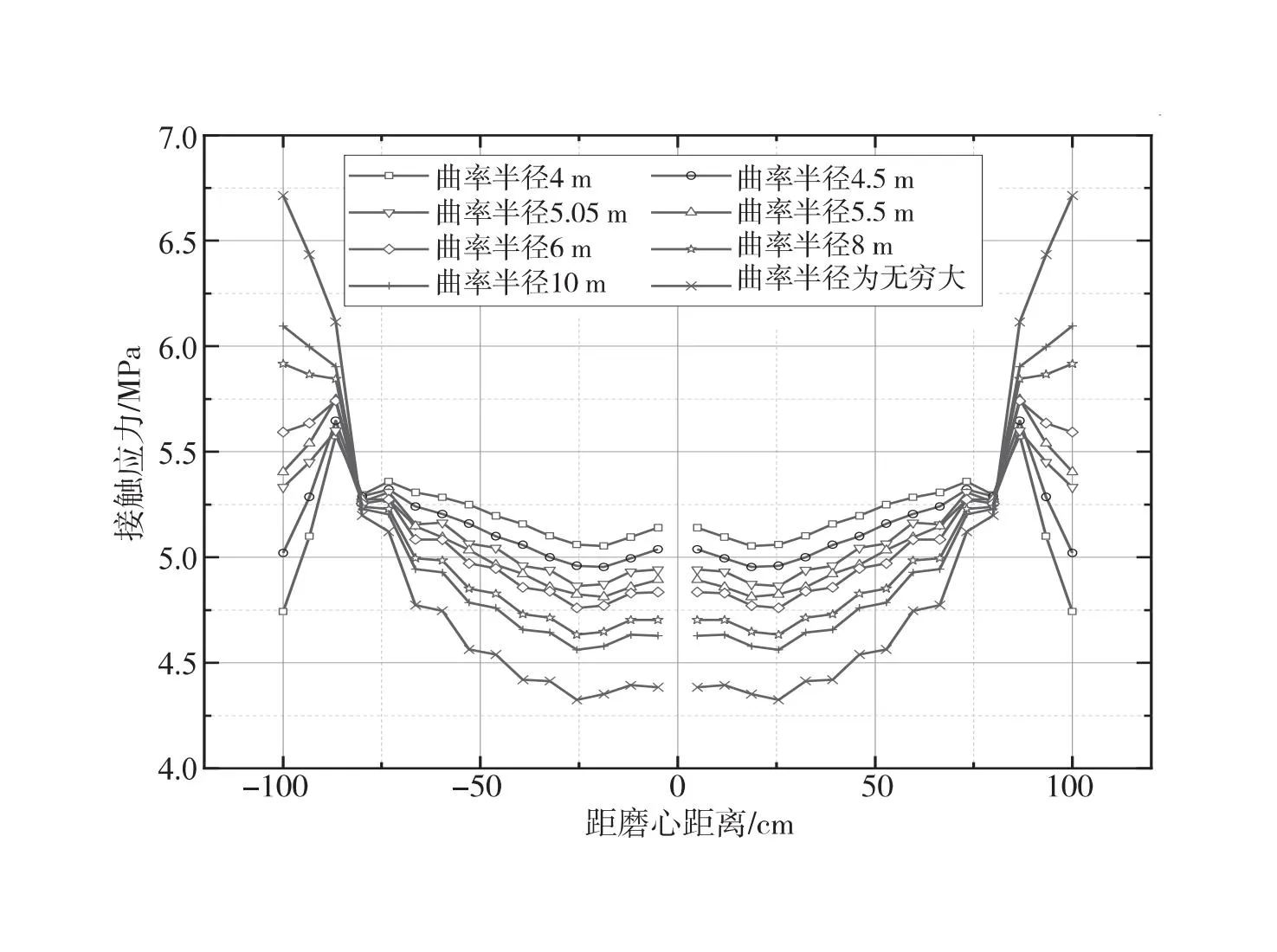
图2 不同曲率半径下球铰的接触应力

2.2 支承半径对球铰接触应力的影响

不同支承半径下球铰的接触应力如图3所示,可以看出:随着支承半径的增加,球铰的接触应力不断减小。当支承半径(Rf)为0.7 m时,球铰最大接触应力为12.12 MPa,当Rf为2 m时,球铰最大接触应力为1.051 MPa。此外,随着支承半径(Rf)的增大,球铰结构曲面上的接触应力分布更加均匀。

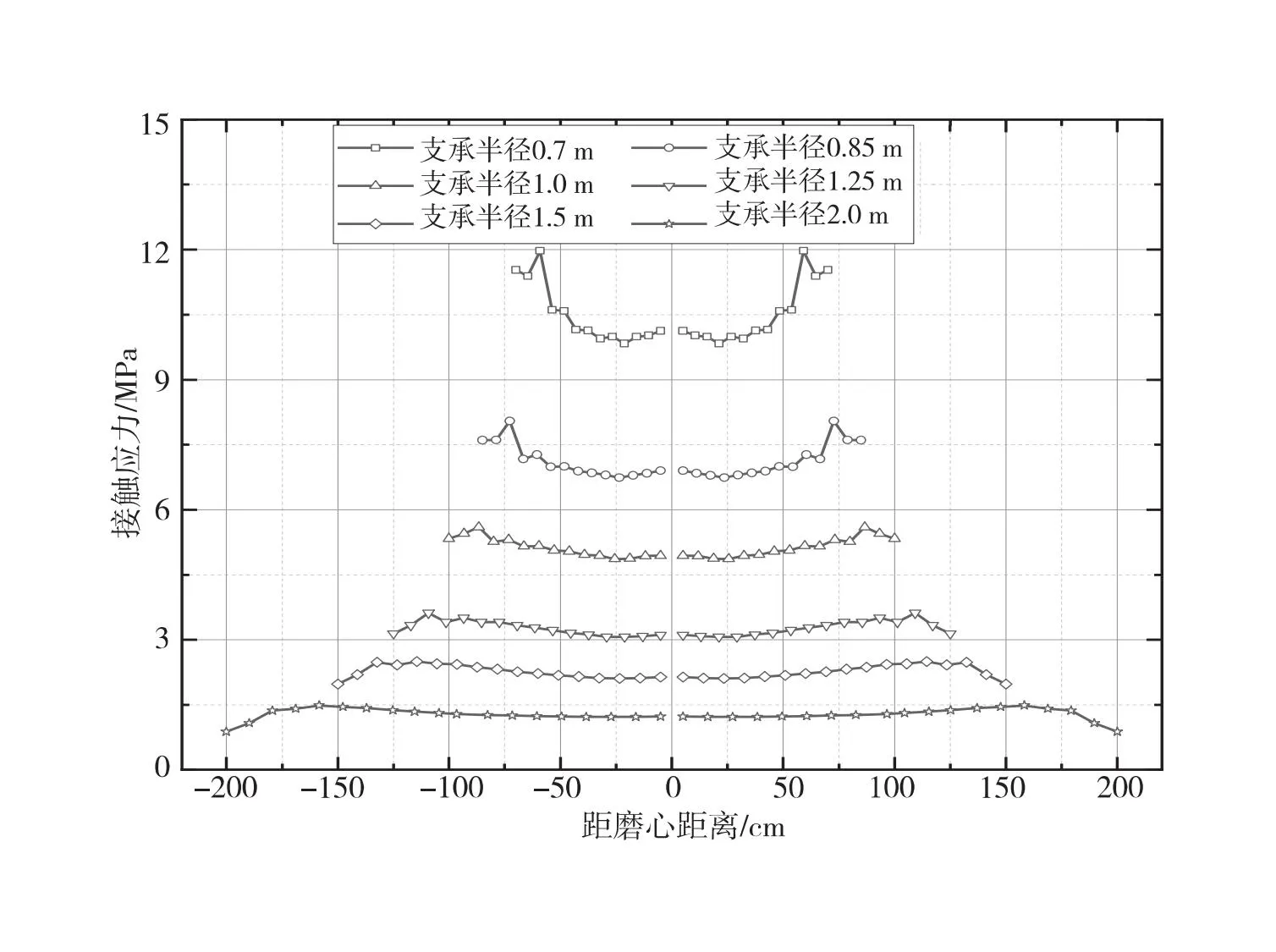
图3 不同支承半径下球铰的接触应力

2.3 下球铰露出高度对接触应力的影响

不同露出高度下球铰的接触应力如图4所示,可以看出:当下球铰露出高度(Hi)为0 cm时,最大接触应力为6.12 MPa;随着下球铰露出高度(Hi)的持续增大,最大接触应力值逐渐降低;当下球铰露出高度Hi为30 cm时,球铰最大接触应力值降低为5.52 MPa;当球铰高度(Hi)大于15 cm时,球铰接触应力沿径向变化幅度较大,不利于转体施工安全顺利地进行。因此,当支承半径为1 m,曲率半径为5.05 m时,下磨心露出高度(Hi)应控制在5～15 cm。

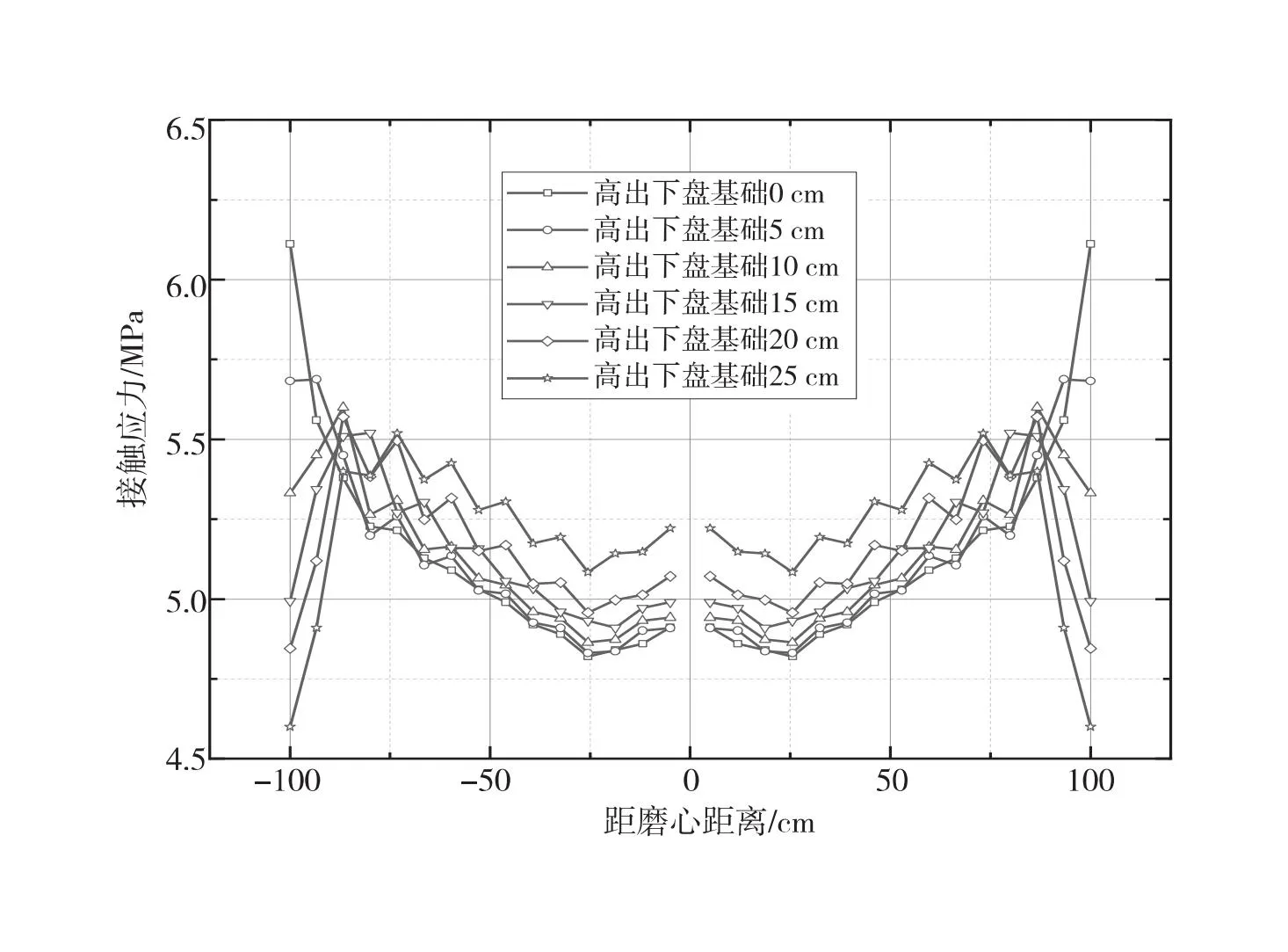
图4 不同露出高度下球铰的接触应力

3 响应面法影响性评价

3.1 响应面法设计方案

响应面法实质上属于一种统计方法:用函数来拟合影响因素与响应值之间的关系并找出最佳组合的影响因素[8]。在本文响应面法分析中,影响因素为3种设计参数,即曲率半径(Rs)、支承半径(Rf)以及球铰露出高度(Hi),以最大接触应力CPRESS作为响应值。

下面采用Design-Expert软件的Box-Behnken设计方法对球铰结构受力的影响因素进行定量分析。外切中心复合设计方案共17组(见表2),对应建立17组影响因素对应的有限元模型,获取其接触应力、等效应力以及摩阻力矩。基于Design-Expert软件得出的最大接触应力方程、最大等效应力方程、摩阻力矩的影响因素与响应值之间的回归曲线方程如下式所示。

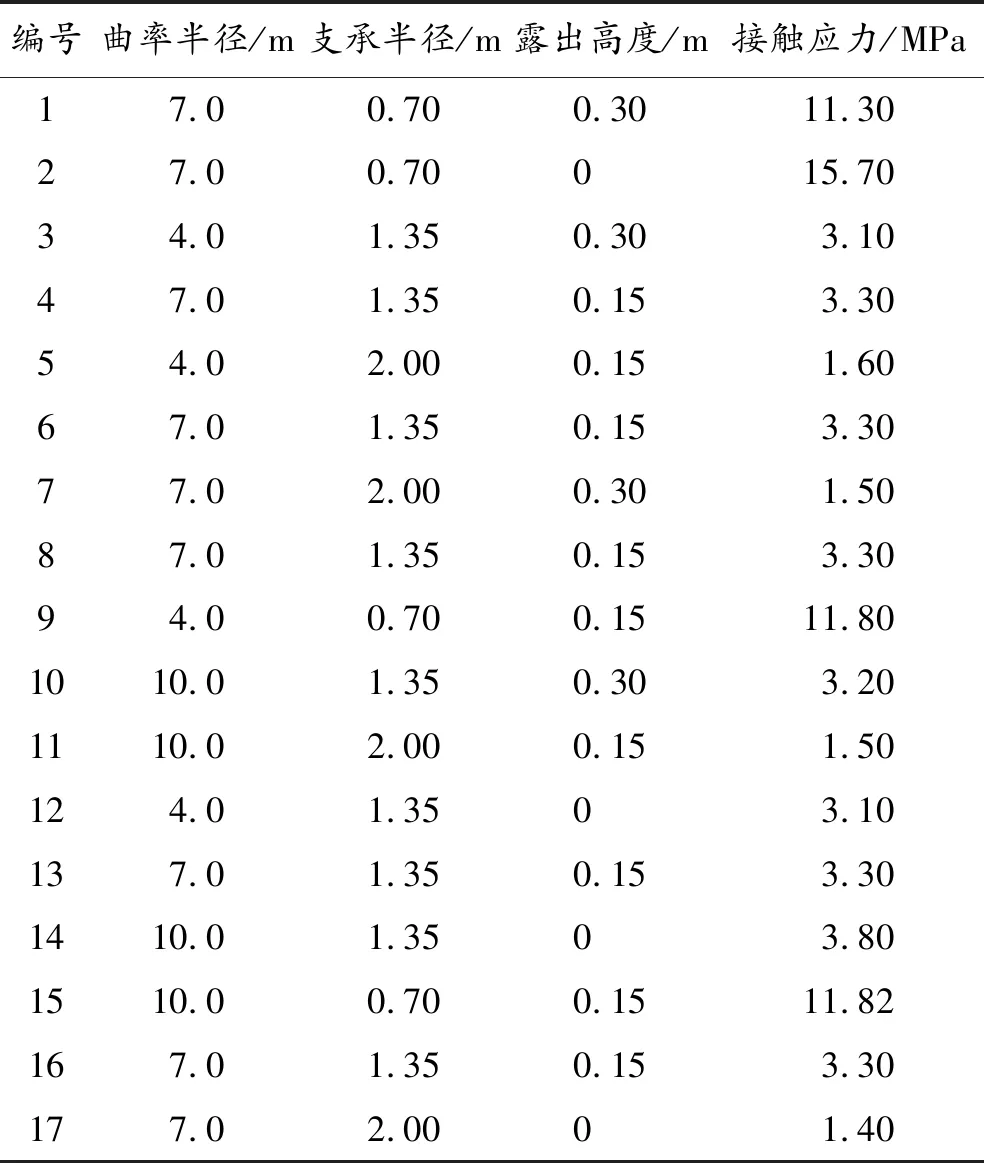
表2 外切中心复合设计方案

(1)

式中:Rs为曲率半径;Rf为支承半径;Hi为下球铰露出高度。

3.2 响应面法结果分析

通过获取Design-Expert软件的方差分析结果来反映球铰的曲率半径、支承半径以及下球铰露出高度这3项设计参数对于响应值最大接触应力的相关性。需要指出的是,f值表示影响程度大小,f值越大,表明该因素对响应值影响程度越大,而p值越小,表明该因素对响应值的影响显著性越大,当p值小于0.01时为非常显著,p值小于0.05时为显著,其结果如表3所示。

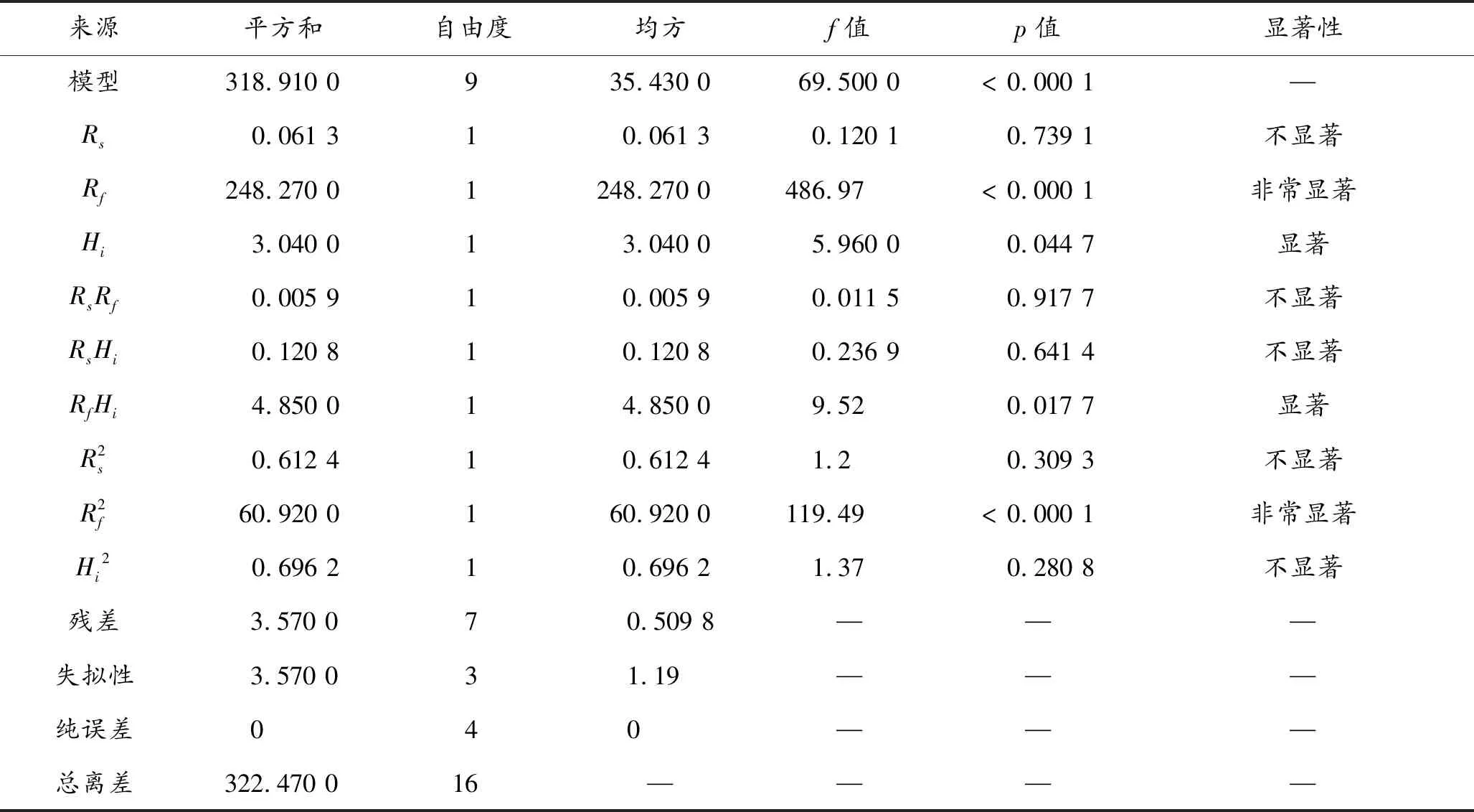
表3 最大接触应力回归模型系数的方差和显著性分析

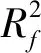
4 结论

本文通过建立混凝土球铰结构的精细化三维有限元模型,探究了曲率半径、支承半径以及下球铰露出高度等参数对球铰结构接触应力的影响,发现随着球铰曲率半径的增大,最大接触应力小幅增大且分布越不均匀;随着支承半径的增大,接触应力不断减小且分布越均匀;当球铰高度大于15 cm时,接触应力沿径向变化幅度较大,不利于转体施工,建议实际施工中下球铰露出高度控制在5～15 cm。最后,基于响应面法的影响性分析表明,支承半径对球铰接触应力的影响最大,其次是露出高度和曲率半径。