仿生刀齿减阻性能数值模拟

冯艳艳，唐亚鸣，时安德，谢 瑶

(河海大学机电工程学院，江苏 常州 213022)

土壤黏附是疏浚挖泥船在施工过程中无法避免的现象，尤其在挖掘黏性土壤时。由于从仿生学角度出发进行产品设计已成为一种新的途径，因此本文基于在水下生存并且不易粘土的河蚌外壳进行减粘减阻挖掘机具的仿生设计，其中绞刀就是最直接和最核心的土壤挖掘部件。目前，研究土壤切削问题的方法主要有3种：理论研究、数值模拟和试验研究。本文基于有限元方法(FEM)建立绞刀刀齿切削土壤有限元模型，对比分析仿生刀齿和普通刀齿的切削阻力，验证仿生刀齿的减阻效果，以期为绞刀的加工和减粘减阻设计提供可靠依据。

1 棱纹形仿生疏浚绞刀刀齿的设计

设计的前期工作[1]为使用逆向工程技术对河蚌外壳表面进行曲线曲面重构和特征点的数据拟合，为最终建立河蚌外壳表面的数学模型做好准备工作。由于河蚌外壳表面具有类似棱纹形的几何结构，因此数据点的分布高度符合正弦函数y=asin(bx+c)，其中a，b，c分别为振幅、周期和初相位，同时考虑到刀齿的实际尺寸和加工工艺等方面的因素，设定仿生疏浚绞刀刀齿的棱纹形几何结构的数学模型方程为：

y=3.5sin(0.5x)

(1)

单个棱纹形几何结构断面如图1所示，图中单位为mm。

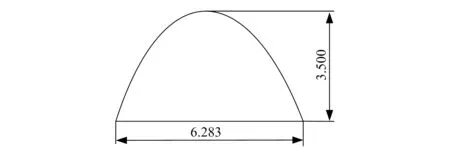
图1 棱纹形几何结构断面图

根据数学模型方程(1)，利用SolidWorks软件设计出3种不同间距分布的棱纹形仿生疏浚绞刀刀齿，如图2所示(L为相邻两个棱纹的分布间距，其他参数相同)。

图2 不同间距分布的棱纹形仿生疏浚绞刀刀齿

2 有限元模型的建立

2.1 土壤模型

在数值模拟疏浚绞刀刀具切削土壤的过程中，土壤本构模型和土壤材料参数的取值对仿真结果有很大的影响[2]。由于疏浚刀具的工作环境大多为水下，作业对象以黏土为主，因此本文选取黏土为切削对象，即本文采用LS-DYNA971中提供的MAT147(MAT_FHWA_SOIL)土壤材料模型，该材料采用修正的Drucker-Prager塑性模型[2-4]，修正后屈服面F的表达式为[3]：

ccosφ=0

(2)

式中：P为压力；φ为内摩擦角；J2为应力张量的第二不变量；K(θ)为张量平面角的函数；c为粘聚力；Ahyp为修正后的Mohr-Coulomb屈服面和标准的Mohr-Coulomb屈服面相似程度。

本文土壤模型的主要参数取值见表1，其余参数取值参考MAT147的默认值[3]。

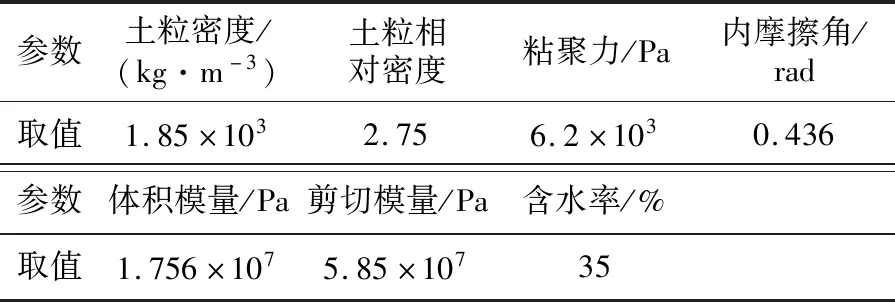
表1 土壤的主要参数

2.2 绞刀刀齿模型

在实际疏浚作业过程中，疏浚绞刀大多采用45钢铸造而成，因此本文选择ANSYS/LS-DYNA材料库中提供的Rigid Material(刚体材料)模型来定义绞刀刀齿材料。刀齿的材料参数取值如下：密度为7.8×103kg/m3，弹性模量为2.0×1011Pa，泊松比为0.3。模型中对刀齿X,Z方向的位移和X,Y,Z方向的旋转进行约束。

2.3 疏浚绞刀刀齿切削土壤仿真模型的建立

2.3.1仿真模型的假设

疏浚绞刀刀齿切削土壤的过程很复杂，应力和应变会随着切削的进行而发生急剧变化，其中含有塑性变形、弹性变形和断裂变形等因素[5]，为准确模拟整个切削过程，对仿真模型及过程做如下假设：

1)在ANSYS/LS-DYNA中建立的土壤模型结构一致，土壤中不存在杂物。

2)假设整个切削过程中只有疏浚铰刀刀齿运动，土壤保持不动。

3)假定疏浚铰刀刀齿速度的大小和方向始终保持不变。

2.3.2仿真模型参数的设置

对仿真模型的参数设置如下：

1)仿真模型中刀齿和土壤均选择ANSYS/LS-DYNA中提供的Solid164实体单元，采用单点积分算法和Lagrange算法。单点积分算法可以减少CPU运算时间，但也可能会产生沙漏模式，可以通过均化网格、增加模型刚度和调整模态的体积黏性等方法来适当减轻沙漏变形现象[4,6]。

2)采用面面接触(surface to surface)中的侵蚀接触(ESTS-Eroding)。PART1的材料号是MAT1，表示刀齿模型，作为接触部件，划分的网格数量为700；PART2的材料号是MAT2，表示土壤模型，作为目标部件，划分的网格数量为80 000。

3)施加全约束于土壤底部，另外为了避免边界处土壤受到模型以外土壤的反射作用对求解域的影响，对土壤Y方向的位移采用无反射边界条件进行约束。

4)在进行切削时，土壤保持不动，疏浚绞刀刀齿做切削运动，只需定义刀齿Y方向的速度就可以完成切削，设置初始状态刀齿沿Y方向的速度为0.8 m/s。

2.3.3土壤-疏浚绞刀刀齿初始模型

把SolidWorks设计的3种仿生刀齿(为了节省计算时间，本文仿真中仿生刀齿的尺寸为设计尺寸的五分之一)保存为.x_t格式文件，直接导入到ANSYS/LS-DYNA中进行网格划分[7]。本文采用稳定性较好的平面四边形单元对刀齿和土壤进行网格划分，为了更精确地分析切削过程中的受力情况，在划分网格的时候将土壤分成两部分，与刀齿接触的部分网格划分较密，不与刀齿接触的部分网格划分较稀疏。普通刀齿和仿生刀齿切削土壤的有限元模型如图3所示。

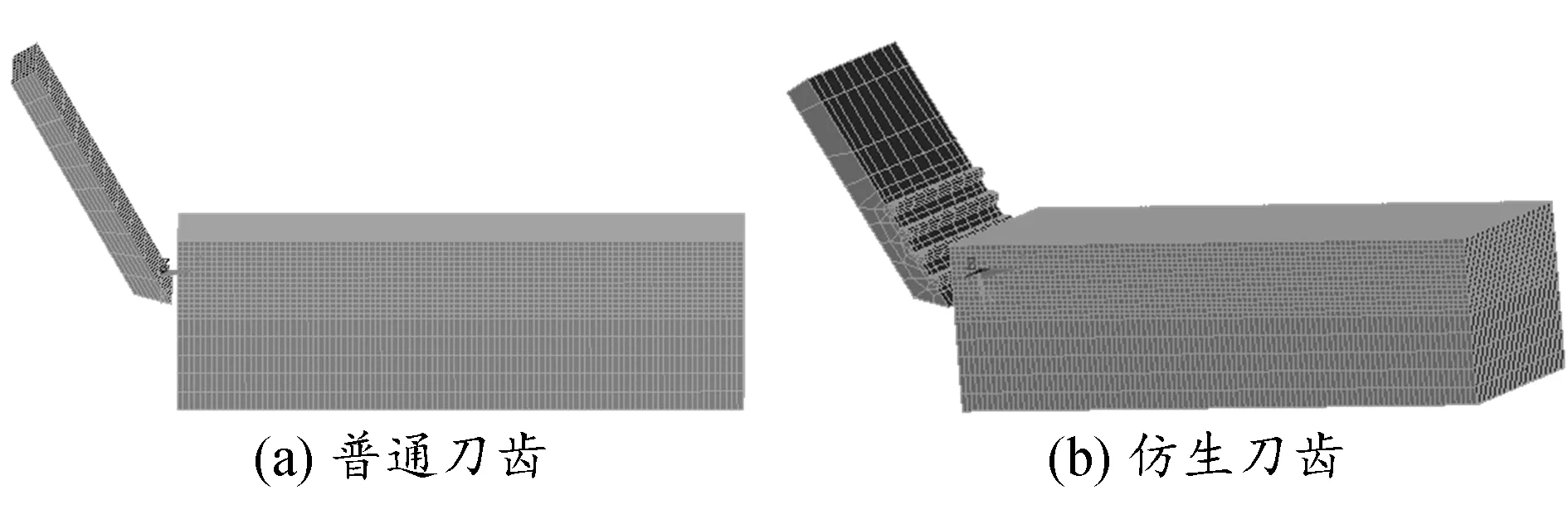
图3 刀齿切削土壤有限元模型

3 疏浚绞刀刀齿切削土壤仿真结果分析

3.1 切削过程

如图4所示，普通刀齿切削土壤的初始阶段，刀齿刃部开始与土壤接触，刀齿沿切削速度方向和垂直于切削速度方向的切削力作用于土壤，使其受到剪切作用而失效。刀齿继续向前切削，土壤受到刀齿的剪切、挤压破坏更加严重，刀齿对土壤的破坏效应也就急剧增加，后面还未与刀齿接触的土壤受到前面被刀齿剪切破坏后土壤的挤压也慢慢开始失效，导致后面土壤的剪切力受到破坏，刀齿受到的切削阻力也就越来越小。普通刀齿的切削力随时间变化曲线如图5所示。

图4 切削过程组图

图5 普通刀齿的切削力随时间变化曲线

3.2 切削力分析

在切削条件相同的情况下，对比分析普通刀齿和3种仿生刀齿的切削阻力大小，以此探究仿生刀齿的减阻效果。由图5可知，在0～1.00 ms切削力波动较大，1.00～3.00 ms切削力趋于稳定，因此选取稳定切削阶段(即本次模拟的1.00～3.00 ms)来对比分析普通刀齿与仿生刀齿切削力的大小。

1)图6为普通刀齿和棱纹间距为10.00 mm的仿生刀齿切削力与时间关系图。从图中可以看出，在初始切削阶段(即1.00～1.25 ms)，仿生刀齿的切削力大于普通刀齿的切削力，这可能是由于大量土壤堆积在第一条棱纹附近导致仿生刀齿的切削力增大；随着刀齿继续切削土壤，堆积在第一条棱纹附近的土壤向四周分散或向刀齿上方滑动，仿生刀齿所受到的切削阻力会随之降低，在1.25 ms以后，仿生刀齿的切削力会逐渐降低，特别是在2.00 ms以后，仿生刀齿的切削力会明显小于普通刀齿的切削力。在稳定切削阶段，普通刀齿的平均切削力为12.13 N，仿生刀齿(L=10.00 mm)的平均切削力为11.00 N。

图6 普通刀齿和仿生刀齿(L=10.00 mm)切削力与时间关系图

2)图7为普通刀齿和棱纹间距为12.50 mm的仿生刀齿切削力与时间关系图。从图中可以看出，普通刀齿的切削力和棱纹间距为12.50 mm的仿生刀齿切削力基本上维持在同一水平，说明棱纹分布间距为12.50 mm的仿生刀齿减阻效果不明显。在稳定切削阶段，普通刀齿的平均切削力为12.13 N，仿生刀齿(L=12.50 mm)的平均切削力为11.85 N。

图7 普通刀齿和仿生刀齿(L=12.50 mm)切削力与时间关系图

3)图8为普通刀齿和棱纹间距为15.00 mm的仿生刀齿切削力与时间关系图。从图中可以看出，棱纹间距为15.00 mm的仿生刀齿切削力明显大于普通刀齿的切削力，这可能是棱纹间距分布过大，导致土壤塌陷，土壤完全包住棱纹，产生挤压变形，从而导致土壤内部的摩擦力急剧增加，同时增大了切削阻力。在稳定切削阶段，普通刀齿的平均切削力为12.13 N，仿生刀齿(L=15.00 mm)的平均切削力为14.42 N。

图8 普通刀齿和仿生刀齿(L=15.00 mm)切削力与时间关系图

为了进一步探索棱纹间距分布对仿生刀齿切削力的影响，又分别模拟了棱纹间距为7.50 mm、8.75 mm和11.25 mm的仿生刀齿切削土壤的情况，得出的平均切削力分别为12.50 N、11.87 N和11.39 N。表2为不同间距分布的棱纹形仿生疏浚绞刀的减阻率。由表2可知，并不是所有的棱纹形仿生疏浚绞刀刀齿都能达到减阻效果，只有合理地分布棱纹形结构单体才能减小切削阻力，本文中棱纹间距为10.00 mm的仿生刀齿具有最佳的减阻效果，其减阻率为9.32%。

4 结束语

本文利用ANSYS/LS-DYNA软件，模拟分析仿生疏浚绞刀刀齿切削土壤的过程，通过与普通刀齿的切削阻力作对比，可知不是所有的棱纹形仿生疏浚绞刀刀齿都能达到减阻效果，只有合理地分布棱纹形结构单体才能减小切削阻力。本文的研究结果可为仿生疏浚绞刀刀齿的参数优化设计提供参考。

表2 仿生刀齿减阻率