2∶1内共振下超临界输流管道的强迫振动

王则, 耿佳, 李满枝

(1.太原科技大学应用科学学院, 太原 030024; 2.西安交通大学机械工程学院, 西安 710049; 3．中国商飞上海飞机设计研究院, 上海 201203)

管路系统是支撑飞机、火箭等飞行器安全飞行的重要系统之一。由于外部激励、内部流体以及管道的相互作用,管道呈现复杂的振动行为,导致管路系统经常发生振动故障,严重影响飞行器的安全飞行[1-3]。当前飞行器管路系统中流体的流速越来越高,使得管路系统的振动问题更加突出。

输流管道的振动问题属于非线性问题的范畴,研究人员采用多种方法对其进行了广泛的研究。王鹏等[4]综述了输气管道瞬态响应的研究方法。徐玲等[5]基于离散元与有限元耦合的方法研究了输气管道的稳态动力响应。这些针对低流速下输流管道的研究都表明其响应存在多种有趣的现象[6-7]。然而,当流体的速度超过临界速度时,输流管道的响应呈现更加复杂的振动行为。Tan等[8]使用伽辽金离散截断法研究了超临界流速下的固有频率,表明在超临界流速下,固有频率随着流速的增加而增加。此后,Tan等[9]和黄慧春等[10]分别使用有限差分法和直接多尺度法研究了超临界流速下管道的非线性主共振,表明在超临界流速下其响应呈现软弹簧特性。李钱[11]使用值积分法研究了输流管道随流速的分岔行为,表明在超临界流速下输流管道存在混沌振动。

内共振,即系统的固有频率间存在近似整数比的关系,广泛存在于许多工程问题中。当系统存在内共振时,两个模态间可能发生相互作用,导致能量在两个共振模态间传递。毛晓晔等[12]使用多尺度法研究了超临界输流管道具有3∶1内共振时强迫振动响应。张凯凯等[13]使用多尺度法研究了参数激励下超临界输流管道的振动响应。这些研究表明,内共振使得系统能量在模态间相互传递。此外,Zhang等[14]和黄慧春等[15]使用多尺度法研究了超临界输流管道具有2∶1内共振时的振动行为,表明系统存在对称的双跳跃现象。然而,Zhang等的研究没有考虑三次非线性项的影响,也没有考虑系统响应的分岔行为研究。

综上所示,针对超临界输流管道内共振的研究亟待解决。因此,现针对超临界流速下输流管道的非线性振动行为,聚焦其在2∶1内共振条件下解的稳定性和分岔行为,并分析各个系统参数对系统响应的影响,以期为高速流体管道的动力学设计提供指导。

1 运动方程

图1所示为典型输流管道的示意图,管道两端的支撑简化为简支边界。管道的运动方向垂直于管道的轴线。假设管道为细长柔性结构,因此可不考虑剪切变形和转动惯量的影响。考虑运动时管道轴向伸长引起的非线性轴向力,基于牛顿第二定律,输流管道在外界简谐激励作用下的运动方程[16]可写为

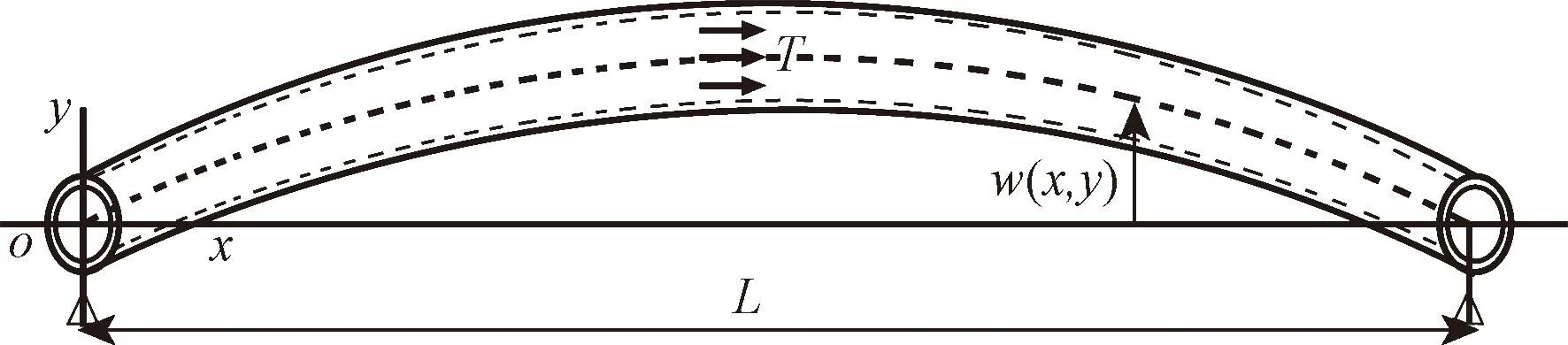
图1 输流管道的示意图Fig.1 Schematic representation of fluid-conveying pipe

(1)

为方便研究,引入以下无量纲参数:

(2)

将无量纲参数式(2)代入式(1),得输流管道的无量纲方程为

(3)

管道两端为简支边界,则无量纲的边界条件为

υ(x,t)=0,υ″(x,t)=0,x=0,1

(4)

当流速超过临界流速后,输流管道的平凡构型发生失稳,分岔为两个对称的非平凡构型,其平衡构型的表达式为

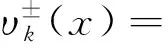
(5)

式(5)中:k表示临界速度阶数,且只有第一阶非平凡构型为稳定的。

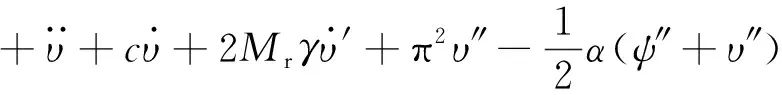
(6)

式(6)为非线性的偏微分方程,一般不存在解析解。其可使用Galerkin截断法求解,假设式(6)的解为

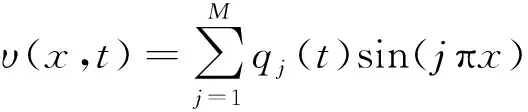
(7)

式(7)中:qj(t)表示横向振动的第j阶模态坐标。将式(7)代入式(6),并将所有项乘以sin(πx),然后将得到的方程在x=0到1上积分,可得到以下常系数非线性微分方程为

(8)

式(8)也可写作矩阵形式,即

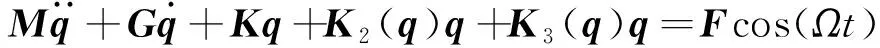
(9)

式(9)中:M为质量矩阵;G为陀螺矩阵;K为线性刚度矩阵;K2(q)为平方非线性刚度矩阵;K3(q)为立方非线性刚度矩阵;F为激励幅值矩阵。

2 增量谐波平衡法

在所有求解非线性常微分方程的方法中,增量谐波平衡法是一种高效可靠的方法。因此采用增量谐波平衡法求解系统的非线性动力学响应[15]。为求解方程,首先引入新的时间变量τ=Ωt,则式(9)可写成

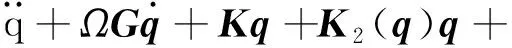
(10)

增量谐波平衡法的第一步是增量过程。假设qi0和ω0表示式(10)的解,则其临近的状态可表示为

qj=qj0+Δqj,Ω=Ω0+ΔΩ

(11)

将式(11)代入式(10),略去高阶小量,得到以下线性增量方程,即

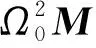
(12)

(13)

式中:R为误差向量;当Ω0和q0为式(10)的准确解,即

q0=[q10,q20,…,qn0]T, Δq0=[Δq1,Δq2,…,Δqn]T

增量谐波平衡法的第二步是谐波平衡过程。由于式(10)具有二次非线性和三次非线性,其稳态解周期解可假设为

(14)

Δqj0=CΔAj

(15)

式中:nc为余弦谐波项的个数;ns为正弦谐波项的个数;C=[1,cosτ,cos2τ,…,cos(nc-1)τ,sinτ,sin2τ,…,sinnsτ];Aj=[aj1,aj2,…,ajnc,bj1,bj2,…,bjns];ΔAj=[Δaj1,Δaj2,…,Δajnc,Δbj1,Δbj2,…,Δbjns]。

令

A=[A1,A2,…,An]T, ΔA=[A1,A2,…,An]T,

S=diag[Cs,Cs…,Cs]

(16)

于是

q0=SA, Δq0=SΔA

(17)

将式(16)代入式(12),并运用Galerkin过程,得到关于ΔA,ΔΩ的线性方程为

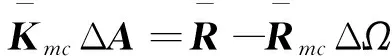
(18)

式(18)中:

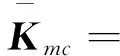
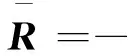
式(17)的未知量比方程的数量多1,计算时可将其中一个未知量指定为增量。若以激励频率为增量,此时ΔΩ=0。求解方程得到ΔA,把ΔA加到原来的解上,得到新的解A+ΔA作为新的解,判R的值是否小于给定的精度;如果不能,继续将A+ΔA代入式(17)迭代,直到满足精度。之后,给Ω一个新的值,重复以上过程。方程解的稳定性可采用多变量Floquet理论求得。

3 数值算例

为了研究输流管道含有内共振时的响应以及各个系统参数对系统响应的影响。本小节采用频率响应曲线表明系统的响应。求解过程中,采用四阶Galerkin截断法,得到一组非线性常微分方程组。在使用增量谐波法求解时,取ns=5,nc=4,令

qi=Ai0+Ai1cos(τ+φi1)+Ai2cos2(τ+φi2)+…,i=1,2,3,4,

图2所示为系统不含内共振时前两阶模态主谐波的频率响应曲线。激励频率被调至第一阶固有频率附近。图2中曲线的无量纲系统参数为:γ=4,Mr=0.447,P=0,α=16,c=0.04。图2(a)为A11的频响曲线,图2(b)为A22的频响曲线。A11为变量q1第一阶主谐波的幅值,A22是变量q2第二阶主谐波的幅值。由图2可知,系统呈现软弹簧特性的非线性。比较谐波的幅值可知,第二阶模态的幅值很小,表明能量主要集中在第一阶模态。具体地,当激励频率从Ω=10开始增加,系统响应的幅值增加,直到在A点发生鞍结点分岔。在该点,解失去稳定性,响应幅值随着激励频率的减小而增加,直到在B点再次发生鞍结点分岔。此后响应再次获得稳定性,响应幅值随着激励频率的增加而减小。

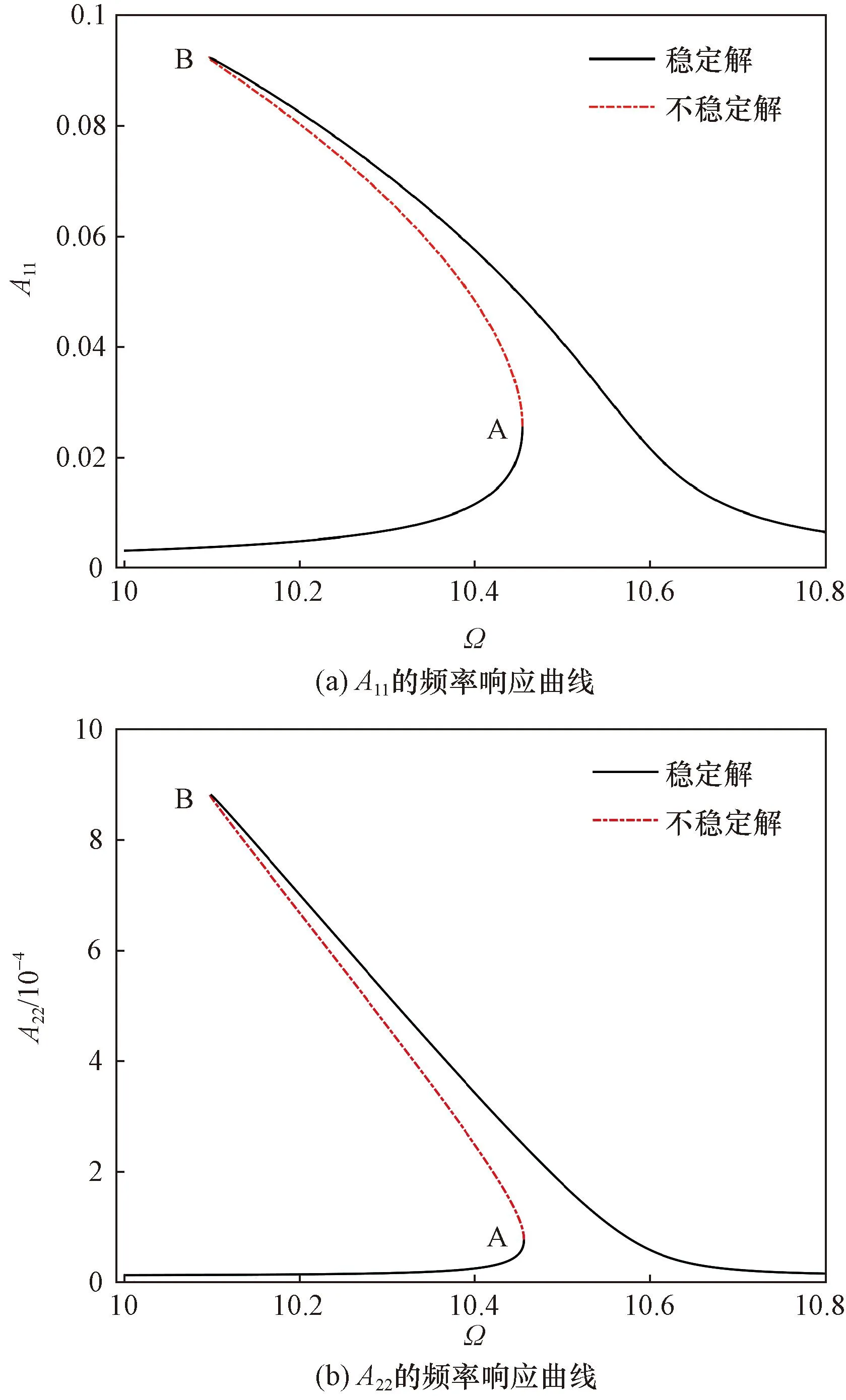
图2 系统不含内共振时的频率响应曲线Fig.2 Frequency response curves of the system with no internal resonance

为了研究系统含有内共振时的响应。图3给出了系统具有2∶1内共振时的频率响应曲线。为表明图中的曲线,选择输流管道的流速γ=5.427,此时ω2=2ω1。

由图3可知,频率响应曲线存在两个不对称的峰,这与文献[14]中得到的对称的峰不同。究其原因是,三次非线性项使得系统的响应整体向左弯曲。具体地,当激励频率Ω从较小的值开始增加,幅值增加,直到A点,发生鞍结点分岔,响应成为不稳定的。此后解随着激励频率的减小而增加,直到在B点,再次发生鞍结点分岔,响应再次获得稳定性。此后随着激励频率的增加,响应的幅值减小。直到激励频率达到C点,系统发生Hopf分岔,响应呈现非周期解。继续增大激励频率,响应在D点发生反Hopf分岔,响应再次成为稳定的。进一步增加激励频率,幅值增加,直到在E点发生鞍结点分岔,响应失去稳定性,直到在F点,响应再次成为稳定的。激励增加激励频率,响应幅值随着激励频率的增加而减小。

图3表明2∶1内共振会导致系统发生Hopf分岔,响应呈现拟周期行为。为了表明系统发生Hopf时的非稳态响应行为,图4所示为激励频率Ω=17.87时的时域图、傅里叶频谱图、相图和庞加莱截面图。由图3(a)可知,能量在第一阶模态和第二阶模态之间连续交换,导致系统响应呈现拍振现象。此外,傅里叶频谱图表明,此时响应中不仅包含激励频率的成分,也包含其他的频率成分。同时,庞加莱截面图也成一个闭环,表明系统响应为拟周期的。

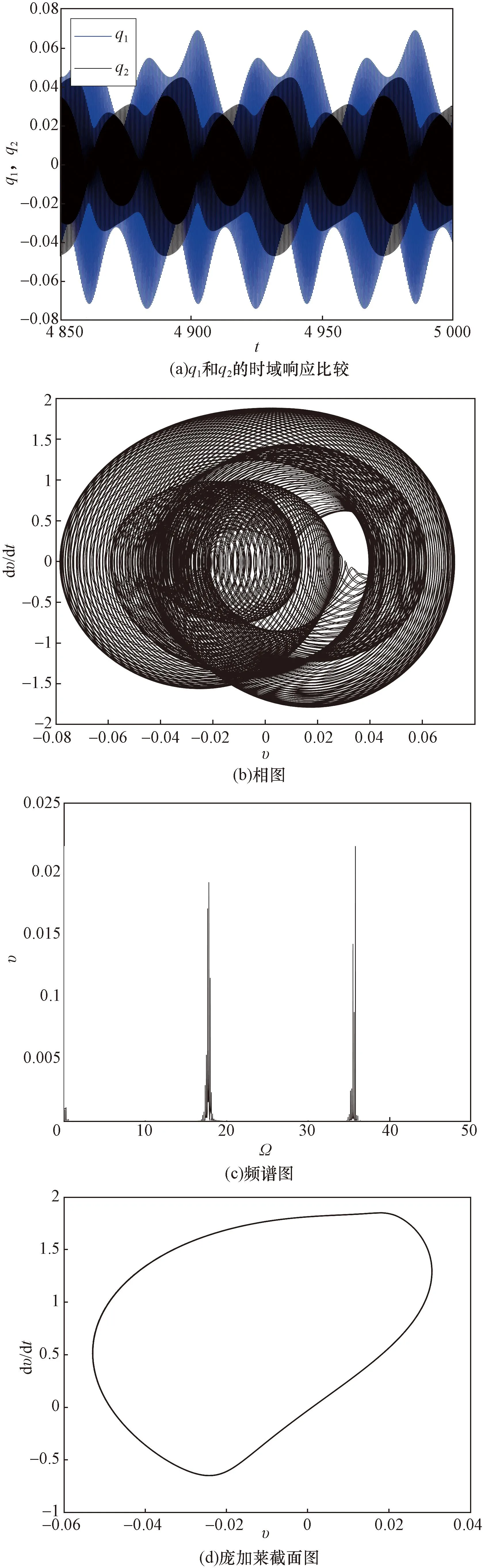
图4 Ω=17.87时的拟周期响应Fig.4 Quasi-periodic response as Ω=17.87

图5所示为阻尼系数对系统频率响应曲线的影响。由图5可知,随着阻尼系数增加,响应的主峰值明显减小;由于2∶1内共振引起的峰值也随着阻尼系数的增加而减小。这表明阻尼能阻碍能量在耦合模态间的能量交换。此外,随着阻尼的增加,由内共振引起的拟周期响应的频率区间也减小。如图6所示为随着阻尼系数变化时系统发生拟周期响应的区间。由图6可知,随着阻尼增加,发生拟周期响应的频率范围减小。

如图7所示为不同激励幅值下系统的频率响应曲线。由图7可知,随着激励幅值的增加,响应的主分峰值和副幅值都增加。这表明,激励幅值增加,模态间的相互作用也增强。此外,随着激励幅值增加,系统发生拟周期响应的频率范围也增加。为了表明拟周期范围随激励幅值的变化,图8给出了不同激励幅值下,系统发生拟周期响应的范围。由图8可知,当激励幅值减小时,拟周期响应的范围减小,直到当激励激励幅值达到0.02时,系统不再发生拟周期响应。

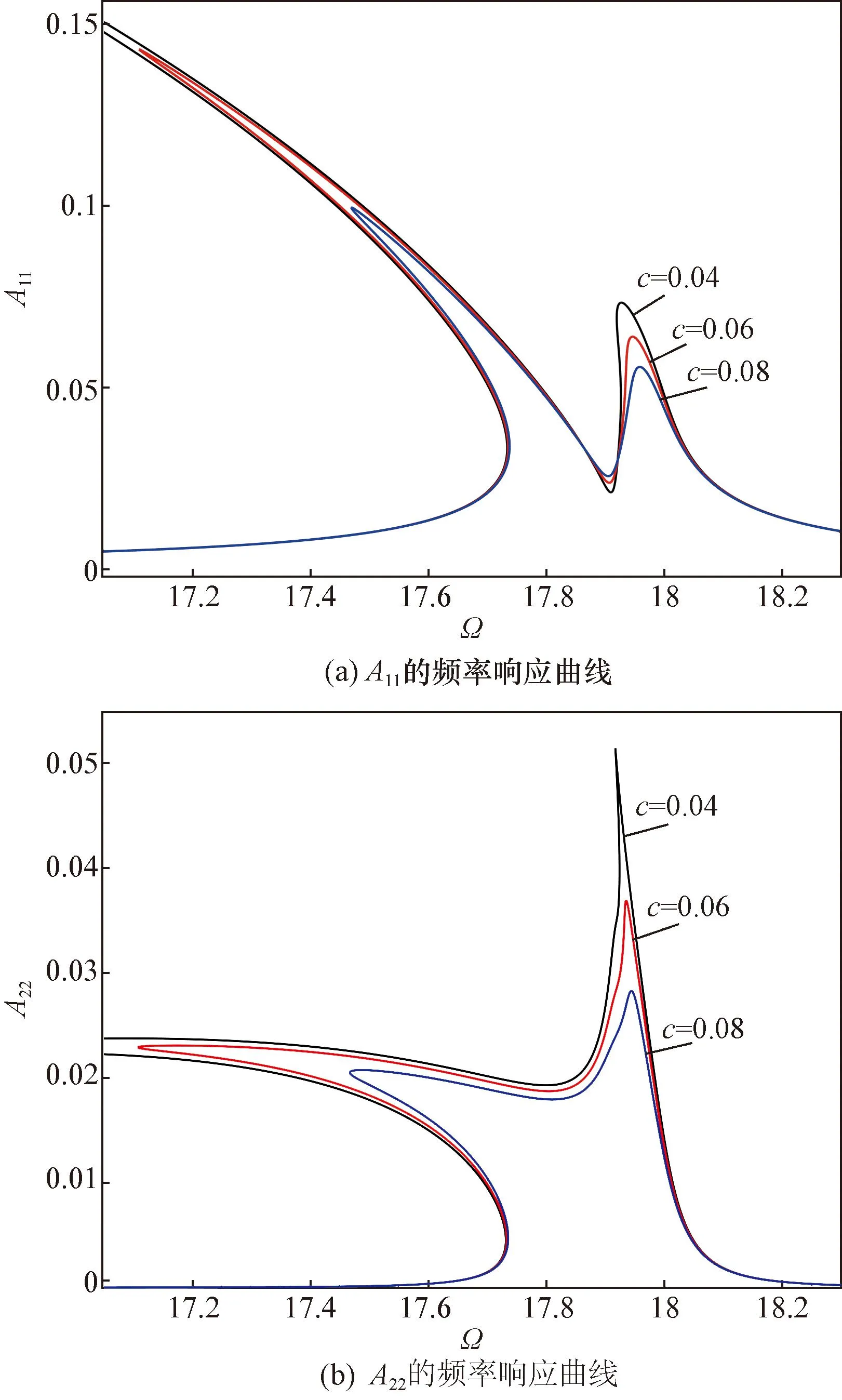
图5 不同阻尼系数下的频率响应曲线Fig.5 Frequency response curves for various damping ceofficient

图6 不同阻尼系数下拟周期解的激励频率区间Fig.6 Range of excitation frequency with quasi-periodic response for various damping coefficient

图7 不同激励幅值下的频率响应曲线Fig.7 Frequency response curves for various excitation amplitude

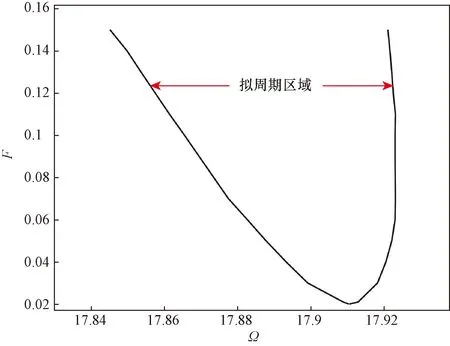
图8 不同激励幅值下拟周期解的激励频率区间Fig.8 Range of excitation frequency with quasi-periodic response for various excitation amplitude

4 结论

以超临界输流管道为研究对象,使用增量谐波平衡法研究其存在2∶1内共振时的动力学响应。利用多变量Floquet理论分析了响应的周期解的稳定性和分岔点,并研究了系统参数对响应的影响。此外,基于时域图、相图、庞加莱截面图、傅里叶频谱图表明了系统的拟周期响应。

研究表明,在2∶1内共振条件下,超临界输流管道呈现出不对称的双跳现象,这种不对称性源自系统三次非线性的影响。在2∶1内共振条件下,当激励频率在第一阶固有频率附近时,系统存在Hopf分岔行为,这导致系统呈现出拟周期振动等复杂响应行为。分析系统参数对响应的影响表明,增加阻尼会降低内共振引起的模态间相互作用。增加激励幅值,可增强模态间的相互作用。