不完备信息条件下基于Roustida改进算法的诊断规则提取

李金艳, 余忠华

(1.江苏科技大学经济与管理学院, 镇江 212003; 2.浙江大学机械工程学院, 杭州 310027)

诊断决策过程本质上为信息的处理过程。由于信息结构的复杂性和采集的局限性使得获取的信息常常存在着缺失、模糊、冗余等不完备现象。如何基于不完备信息进行诊断决策已经成为重要的研究课题。

目前数据值缺失的处理主要有缺损信息删除、可能值插补以及数据挖掘三种方式[1]。删除含有缺失值样本/信息项的方式在样本量不充足或信息维度较高时,易造成信息浪费;数据挖掘方式则是利用贝叶斯[2]、模糊集[3]或证据理论[4]等方法通过建立概率密度函数、隶属度函数或信任函数等直接进行知识挖掘,数据值缺失形成的不确定性对挖掘效果有较大影响的同时,计算复杂度和难度亦是需要考虑的问题[5];可能值插补[6]方式分为统计插补[7]和数据挖掘插补[8],均为数据背景下的估计补齐且均建立在大样本的基础上,插补结果满足统计意义上的合理,工程实践应用时往往无从解释或修正。粗糙集理论(rough set,RS)初始对不完备信息的研究主要集中在缺失值属性处理、不完备对象间相似关系模型建立等方面[9]。经后续基于容差关系、基于量化容差、基于相似关系以及基于限制容差关系等的扩展研究[10],文献[11]认为扩展研究可以进一步实现探寻信息之间的内在联系,数据插补可以提高信息的表层完整性,二者的结合则可以更好地为知识挖掘奠定基础。属性冗余一般指含有多余、无用的信息在其中,进行认知时需对信息降维以消除其中的冗余、噪声等,常用方式有特征选择与特征提取。特征选择[12]是从数据集的原始特征中选择一个特征子集,组成可反映原始特征的低维空间。特征提取[13]则是通过线性或者非线性的方式对原始数据空间进行映射变换,生成维数低且相互独立的特征空间,提取后的新特征是原特征的映射。针对具有冗余性、相关性以及稀疏性等特征的数据集,特征提取可以规避以上缺点,提高数据处理效率的同时保持较好的分类精度,但并存的缺点是所得特征的可理解性差。在尽量不改变原数据信息构成的处理需求下,特征选择更具优势。

粗糙集理论对不确定知识的处理虽然有效[14],但未含处理不完备或不确定原始数据的机制,在解决专业领域问题时需要其他方法补充提高数据分类能力,如与统计方法[15]、证据理论[16]、贝叶斯[17]、遗传算法[18]、模糊集[19]、Petri网[20]、神经网络[21]等。围绕通过问题聚类探寻诊断规则的目标,粗糙集与适当方法结合,从既定的相关情境信息和问题描述出发,通过辨识矩阵和等价类确定问题诊断的近似域,进而挖掘问题发生的隐含知识/规律,无论在理论上还是应用方面都有待深入研究的价值。为此,以信息不完备情形下的诊断决策为研究对象,基于粗糙集理论,首先针对Roustida算法在缺失值处理时存在的局限性进行改进,扩充其在工程实践中的适用范围;然后在扩充辨识矩阵一致性检测的基础上,利用遗传算法和广义诊断规则推理进行特征选择与规则凝练,力求以相对较简方式表达问题征兆与情境域信息之间的关联关系,实现问题诊断决策的条件属性约简与规则提取。

1 信息表征与改进算法

1.1 信息表征

根据RS信息决策表的定义对诊断情境信息进行描述,确定由情境域构成的条件属性集合和由问题征兆组成的决策属性集合。

定义1四元组S=,其中:

(1)对象集合U={ui|i=1,2,…,n}为问题域。

(2)属性集合A={ak|k=1,2,…,m},A=C∪D且C∩D=∅,即属性集合由条件属性集合C与决策属性集合D组成。

(3)值域集合V=∪Va,其中Va表示属性a的值域。

(4)f为UA→V的函数,实现对象的属性赋值。

数据值缺失类型从产生根源角度可分为:①无法取值——生产模式及相关工艺更新,加工要求产生变化,条件属性随着工艺的调整会发生“必要→一般→无关”的更迭变化,导致信息采集、统计时无法填入属性值的现象。②存在但暂时无法获知——条件限制,并非所有状态信息都可以在既定的时间内获得。研究数据信息缺失情况时,一般即指该类属性值缺失。③待定——伴随信息技术发展,大量高速、实时数据日趋常态化,加上工艺的复杂性和更新交替的快速性,认知和描述能力有限的情况下,一些诊断信息无法确定是暂时缺失还是本身便无法填入,需要随着时间的推移方能确认。

1.2 改进算法

Roustida算法利用信息间的不可分辨关系选取相似样本的相应值对缺失数据进行修补。该算法存在一定的局限性,以下情况无法处理:①存在缺失值的实例与其他任何样本对象均不相似;②存在属性值缺失的实例对象与多个样本对象相似。因此,需要对该算法进行改进,以拓展其适用性。

定义2设ΞS=,A=C∪D,C∩D=∅,缺失属性集A*、属性缺失对象集U*和不可辨识对象集IND分别为

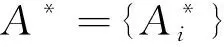
(1)

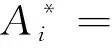
(2)

U*={ui|∃ak∈A[ak(ui)=*],i=1,2,…,n;k=1,2,…,m}

(3)

IND={indi},indi={uj|M(ui,uj)=∅,i≠j}

(4)

其中辨识矩阵

(5)

式中:“∧”为逻辑与,表示同时成立的关系。

若ui与其他任何对象都不相似,即|indi|=∅,传统Roustida算法便无法处理,需结合相关领域背景知识对indi进行相似性拓展:通过问题归类(决策属性),利用其中与之相似程度较高的样本对象的相应属性值进行插补。

定义3扩展相似对象集ind′i:对象ui的扩展相似对象集为

ind′i={uj|D(ui)=D(uj),i≠j,j=1,2,…,n}

(6)

定义4相似度|simij|:∀uj∈ind′i,对象uj与ui的等值属性集为

simij={ak|ak(ui)=ak(uj)∧ak(ui)≠*∧ak(uj)≠*,k=1,2,…,m}

(7)

对象uj与ui的相似度为|simij|。

定义5次相似对象集ind″i:对象ui的次相似对象集

ind″i={uj|max|simij|,uj∈ind′i}

(8)

(9)

此时插补值是由群体值描述:将ui的其他完整属性值与样本集合中的每一个可能值进行组合,形成新的实例对象,改进算法的具体实施流程如图1所示。

2 属性约简与规则提取

2.1 属性约简

设Ψ′=[ψ′C(ui,uj)]n×n为扩充辨识矩阵,其中ψ′C(ui,uj)表示扩充辨识矩阵中第i行第j列的元素(i,j=1,2,…,n),其取值为

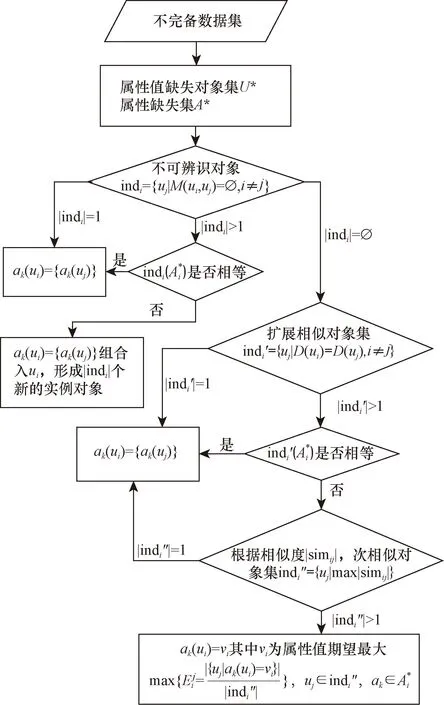
图1 Roustida改进算法的实施流程Fig.1 The implementation process of Roustida’s improved algorithm

(10)

Ψ′=[ψ′C(ui,uj)]n×n包含了所有实例对象的区分信息,其中∅表示条件属性相同,问题征兆(决策属性)却不同,信息表中含有矛盾信息,该条信息不可用。

针对含有的冗余信息,目前已有的约简算法主要是围绕条件属性集C的核CoreD(C)通过启发式搜索寻求最小约简,随着数据规模的增大,其复杂性呈指数倍增长。基于全局优化和隐含并行性的优势,遗传算法可以克服该问题实现求解。

设A′为扩充辨识矩阵Ψ′中所有属性组合的集合:A′={ψ′C(ui,uj)|ui,uj∈U,i,j=1,2,…,n},不包含重复项:Bi∈A′,Bj∈A′,Bi≠Bj(i,j=1,2,…,|A′|)。结合扩充辨识矩阵Ψ′=[ψ′C(ui,uj)]n×n,获取条件属性最小约简的步骤如下。

步骤1考虑情境域诊断信息特点和避免陷入局部最优,采用二进制编码,形成|C|位二进制染色体依次对应条件属性ci。随机产生m个长度为|C|的二进制串作为初始种群,并进行修正以确保不存在编码全为0的空集和全为1的全集。

步骤2围绕诊断条件属性约简的目标,适应函数需要满足:保持约简后属性集合的分类能力,同时确保约简后条件属性量相对最少。即

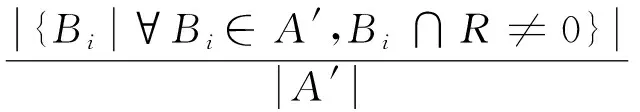
(11)

步骤3以f(R)为目标函数进行优化搜索。

2.2 广义化规则提取

为实现“以相对较简方式描述情境域信息和问题征兆之间的关联关系”的目标,对所得规则进行如图2所示的广义化约简。

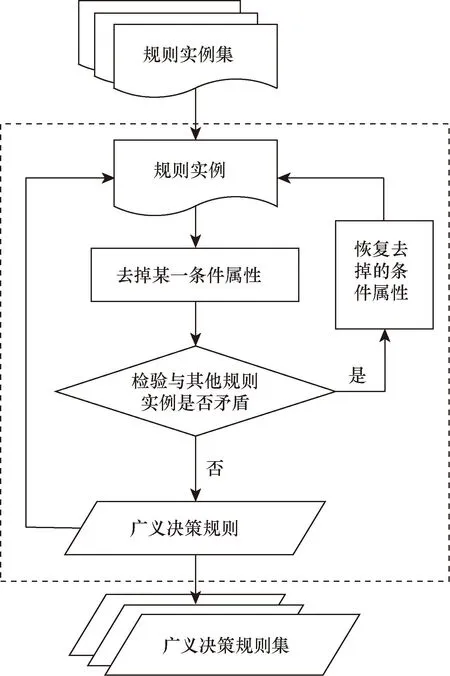
图2 广义化约简流程Fig.2 Generalized reduction process

2.3 评估指标

诊断规则的判断能力可以分两个环节来评估。

(1)属性约简率——评估约简程度

(12)

P越大,原条件属性集合中包含的冗余信息越多。

(2)覆盖度——测度诊断效果

(13)

式(13)中:|C′(u)∩D(u)|为满足规则ri的C′(u)和D(u)的实例数目,即支持规则ri的样本量;|D(u)|为满足诊断规则ri的相同问题征兆的实例数目。该指标反映了所得诊断规则的质量水平:在S中支持ri的实例在与ri具有相同问题的样本实例中所占比率或该条规则ri是基于多少相同问题样本提取所得。

3 应用与讨论

以变进给切入式的滚动球轴承沟道磨削过程中的质量问题诊断为例,机床、砂轮、加工工艺参数等的执行状态直接对加工结果形成影响。

3.1 信息表征

问题诊断信息表S=中各项信息如表1和表2所示。首先Va的离散化:决策属性D={d1,d2},是否发生以{0,1}区分;条件属性C={c1,c2,…,c8}以工艺基准(0)为依据,偏离分别记为{-1,1}。

表1 属性-值域信息Table 1 Attribute-value range information

3.2 不完备信息处理

属性缺失集、属性值缺失对象集、不可辨识样本对象集分别为

A*={c1,c3,c4,c5,c7}

(14)

U*={u1,u2,u3,u5,u8}

(15)

表2 诊断信息表Table 2 Diagnosis information table

ind1=ind2=ind3=ind5=ind8=∅

(16)

因此,可知优先补齐对象|indi|=0,需通过扩展相似对象集求解,即

IND′={ind′1,ind′2,ind′3,ind′5,ind′8} ={(u4,u9,u11,u14,u15,u18),(u7,u12,u16), (u6,u10,u13,u17,u19,u20),(u7,u12,u16), (u4,u9,u11,u14,u15,u18)}

(17)

根据max|Simij|和ind″i可得c3(u1)=0,c1(u2)=0,c4(u3)=0,c5(u5)=0,c7(u8)=-1。

3.3 属性约简与规则提取

根据扩充辨识矩阵Ψ′=[ψ′C(ui,uj)]n×n的一致性检测,ψ′C(u8,u17)与ψ′C(u13,u18)为∅,即u8与u17、u13与u18分别为矛盾信息项。结合背景知识和原始数据分析,判断u17与u18为无效信息项,在诊断信息表中予以剔除。因此,基于以上可得|C|=8,|A′|=|{ψ′C[ui,uj]}|=71,经f(R)优化搜索的条件属性约简集为C′={c2,c3,c4,c5,c8}。

经广义化可得如表3所示诊断规则,其中对象u8:(c3,1)∧(c4,1)→d2,u11:(c3,1)→d2,u14:(c3,1)∧(c5,1)→d2,根据广义化步骤{u8,u11,u14}同时支持(c3,1)→d2。因此,属性约简率P=37.5%。

3.4 诊断规则覆盖度评估

以相同环境下的15个测试样本对上述结果进行覆盖度评估,测试样本信息如表4所示。

根据表5测试结果可知,覆盖度Cor(ri)=86.7%。

表3 诊断规则Table 3 Diagnosis rules

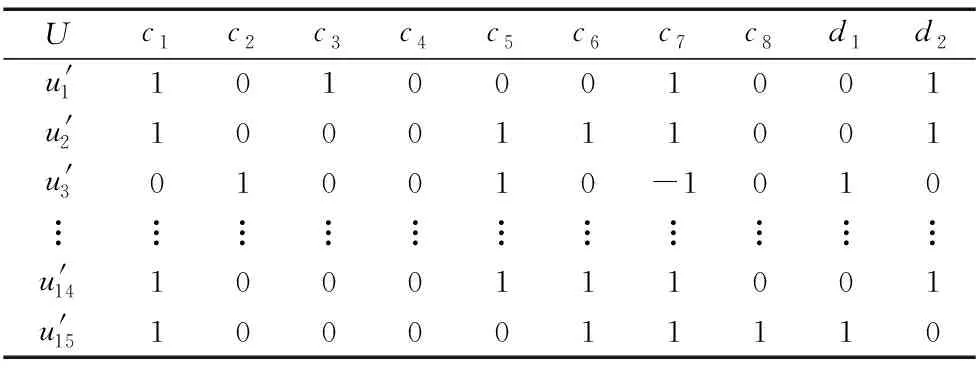
表4 测试实例信息Table 4 Test instance information

表5 测试结果比较Table 5 Comparison of test results

3.5 结果讨论

(1)与其他方法的插补结果比较:如表6所示,K-近邻算法c4(u3)=1,统计意义上无误,但结合u3情境信息可知与实践相悖,无从解释或修正。Roustida算法的假设前提是缺失数据值的填补尽可能反映问题域的基本特征以及隐含的内在规律,使缺失值对象与其他相似对象的属性值之间的差异尽可能小,改进后基于工程背景引入扩展相似对象集、次相似对象集及其相似性评估,避免了结果只满足统计合理性。

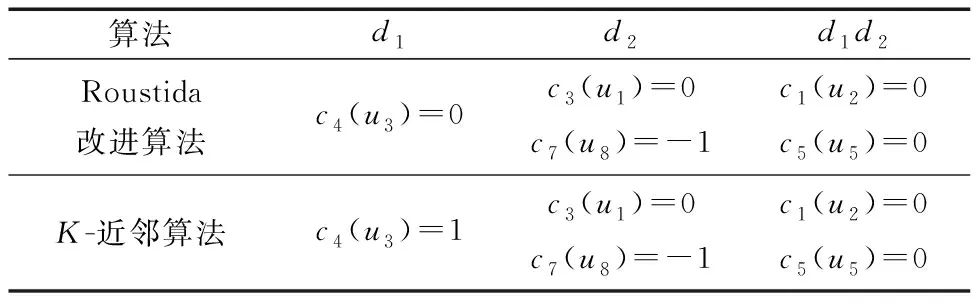
表6 插补结果对比Table 6 Comparison of supplement results

(2)数据处理的影响分析:数据离散化本质上是通过某种断点集合对决策系统的属性进行划分。为提高系统的聚类效果,增强对数据噪声的鲁棒性,采用尽可能少的区间划分。故对源数据在偏差允许范围内以工艺标准为基准做了{-1,0,1}的简化划分处理。诊断决策过程中各项情境信息度量要求较高时,势必对不可辨识关系和辨识矩阵的精确性形成影响。

(3)测试结果的偏差分析:根据工艺c5与d1是反比关系,样本u′3的(c5,1)→d1不成立,经校验d1是由于粗进给形成误差复映的同时光磨时间不足造成,即(c2,1)∧(c7,-1)→d1;样本u′14实际校验为砂轮在运转一定时间后的平衡与表面钝化问题导致,结合工艺应归因于修整间隔不当,即(c1,1)→d2。

4 结论

就如何在属性冗余、数据值缺失情形下通过问题聚类获取诊断所需隐含知识的问题,针对信息补齐与属性约简策略进行了研究,取得了如下研究结果。

(1)针对Roustida算法在工程实践中面临的局限性,结合工程应用提出了相应的改进算法,扩充了不完备信息完整化功能的工程实践范围。

(2)针对诊断信息的不一致问题,利用扩充辨识矩阵剔除其中的矛盾信息项,并在此基础上通过遗传算法设计和广义诊断规则推理实现了条件属性约简与规则提取。

(3)通过实例的验证与测试表明该方法在一定程度上可以保障诊断知识覆盖度;最后针对样本测试结果,从与统计补齐方法比较、处理过程以及工艺分析等方面进行了补充讨论。