基于GWO-CNN-BiLSTM的超短期风电预测

程杰, 陈鼎, 李春, 钟伟东, 严婷, 窦春霞*

(1. 南京邮电大学, 碳中和先进技术研究院, 南京 210023; 2. 南京邮电大学自动化学院、人工智能学院, 南京 210023; 3. 国网浙江省电力有限公司嘉兴供电公司, 嘉兴 314000)

如今,全球经济迅速发展的同时,环境污染和能源危机引发的供需不平衡等问题日益严峻。为解决上述问题,在过去的几十年中,可再生能源如风电得到了迅速发展。“2022全球海上风电大会”提出,为实现全球气温下降1.5 ℃的目标, 2050年全球海上风电累计装机容量至少达到20亿千瓦[1]。为积极响应全球环保目标的号召,到“十四五”末,中国风电累计装机容量须达到1亿千瓦以上。然而,风电因其典型的波动性、随机性、间歇性等特点对电力系统的运行、调度造成了巨大的挑战,因此,针对风电功率的超短期预测研究尤为重要[2-3]。

目前,国内外学者对超短期风电功率预测方面做了大量研究。在预测方法上面可分为物理建模法、统计建模法和人工智能算法[4]。物理建模预测方法在欧美等国家应用广泛,文献[5]基于稳定的计算流体力学模型,建立包括进风条件、流场和风机的相应风功率等重要参数在内的数据库,通过数据库,以数值天气预报为输入数据来预测风电输出功率。由于物理信息收集起来难度较大,且相关环节过于复杂,预测效果并不理想。统计建模法主要通过风电历史数据,构建出风电历史数据与风电功率的非线性对应关系,以此对风电功率进行预测,文献[6]对差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)进行改进,提出了一种确定不同出力特性的风电场风功率时间序列转化为平稳序列所需的最优差分次数的方法。但ARIMA难以实现对波动性较强数据的精准预测。为了改善预测精度,人工智能算法如时序卷积,长短时记忆神经网络等被应用于风电功率预测[7-8]。此外,越来越多的研究聚焦于组合不同机器学习方算法以提升预测精度,如文献[9]中应用包括极度随机树、轻度梯度增强机、集成方法和基于卷积神经网络(convolutional neural network,CNN)与长短期记忆神经网络(long short term memory, LSTM)的组合模型(CNN-LSTM)预测风机功率。文献[10]利用完全集合经验模式分解自适应噪声和支持向量机的非线性拟合特性建立了一个短期功率预测模型,实现风电功率的准确预测。考虑风电功率区间预测问题,文献[11]提出了基于改进型鲸鱼优化算法和快速学习网的区间预测模型,对区间覆盖率的提高具有实际意义。文献[12]提出考虑风电预测误差时序性及风电可信度的双层优化模型,结果表明所提模型能降低系统风险成本。

双向长短期记忆(bidirectional long short term memory,BiLSTM)神经网络,在参考过去信息值的同时,应用未来的信息,以实现时序信息在预测中的效益最大化。文献[13-14]同时利用过去与未来的天气预报信息,提高了风电功率预测的精度。文献[15]基于时间模式注意力(temporal pattern attention, TPA)机制,从BiLSTM网络得到的隐藏行向量中提取多风机间的复杂联系,从而降低预测误差。文献[16]建立了遗传算法改进的双向长短期记忆人工神经网络,用于微电网中不同时间尺度的光伏功率预测。BiLSTM利用时序数据的双向信息值来联系预测关系已经被证明能够有效提高风电功率的预测精度[17-18]。

以上方法均通过信息处理、权重分配、深度学习和模型优化来研究风电预测过程。但是,在利用人工智能算法时,均未深入挖掘智能算法与风电预测的深层联系,算法设参后固定不变,在风电功率与数据的相关性研究方面探讨地不够深入,使得预测精度有一定的局限性。现考虑智能算法主动适应风电数据变化,利用深度学习方法进行预测。

考虑风电场数据与风电功率之间的相关性,现采用CNN与BiLSTM 相结合的神经网络,充分挖掘风电功率的时序特征,并通过灰狼优化算法(grey wolf optimizer, GWO)对神经网络参数进行优化。主要工作包括:

(1)对风电场历史数据进行相关性分析,明确风电参数特征与风电功率的关系,选取相关性较强的风电参数特征投入后续模型训练。

(2)提出CNN-BiLSTM组合深度学习模型,将CNN与BiLSTM结合起来,先对处理后的风电数据利用CNN快速提取数据特征,再通过BiLSTM获取其过去与未来的时序特性,以进行风电功率预测。

(3)为充分挖掘风电特征间深层次联系,进一步提高预测精度,提出GWO-CNN-BiLSTM组合模型,采用GWO对CNN-BiLSTM模型进一步优化,使所提模型的网络参数能够实时地适应风电历史数据,最后将GWO-CNN-BiLSTM模型与CNN-BiLSTM模型在较长时间风况剧烈波动场景下进行风电功率预测对比,结果分析表明本文所提模型能够达到更优的预测性能。

1 CNN-BiLSTM网络与相关性分析

1.1 相关性分析

在实际的风电预测数据中,风电功率往往与风速与风向等特征具有较强的线性相关特性,而与温度、气压以及湿度等特征关系并不明显。在深度学习过程中,呈现极弱相关性的大量数据投入算法训练中,往往会降低预测精度,且使得预测时间过于漫长。原因在于弱相关性特征彼此之间存在深层次的相关性,冗杂的数据输入不仅干扰训练过程,更会影响模型的稳定性。因此,选取合适的风电数据特征进行相关性分析。

在自然科学领域中,皮尔逊相关系数r广泛应用于度量两个变量之间的相关程度,其值介于-1～1之间。皮尔逊相关系数表达式为

(1)

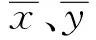
当计算结果为正值时,表示该特征与预测功率呈正相关,其值越大,线性相关程度则越高。通常情况通过表1取值范围判断变量的相关程度。

当计算结果为负值时,则为负相关。判断情况参照正相关。

选取某小型风电场2017年1—2月历史数据进行分析,包括70 m高度风向、70 m高度风速、温度、气压、湿度、空气密度、云量、降水量以及风电场平均发电功率,取样时间间隔为5 min。根据皮尔逊相关系数公式,计算可得各个特征值与风电功率之间的相关系数如表2所示。

表1 相关系数与相关程度表Table 1 Correlation coefficient and correlation degree

表2 各特征值之间的相关系数Table 2 Correlation coefficient between characteristic values

由表2可以看出,对风电预测功率影响最大的参数特征是风速,其相关系数为0.92,表现出极强相关特性;其次依次为风向、气压、温度、湿度,空气密度、降水量及云量,其特征均表现出弱相关或极弱相关性。为避免数据冗杂堆积影响预测精度,不宜考虑呈现极弱相关性特征,所以在下文的模型训练中将风向、风速、气压、温度及湿度五个特征设置为变量投入模型进行训练。

1.2 CNN-BiLSTM网络

1.2.1 卷积神经网络

卷积神经网络(CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,经常被用来处理空间信息丢失、效率低下以及过拟合等问题[19]。CNN结构包括输入层、卷积层、激活层、池化层、全连接层及输出层。

CNN主要结构为卷积层,其内部包含多个卷积核,组成卷积核的每个元素均对应一个权重系数与一个偏差量,来完成特征提取。其原理如图1所示。

CNN卷积层中滤波器可以看作由多个卷积核堆叠形成,其维度小于输入数据维度。通过滤波器在输入数据上滑动完成卷积运算,从而提取特征完成降维。

图1 CNN卷积层原理图Fig.1 Schematic diagram of CNN convolution layer

1.2.2 双向长短期记忆神经网络

为处理长时间序列,研究人员提出了LSTM结构。区别于RNN的重复神经网络模块的链式结构,LSTM重复的模块拥有一个不同的结构,LSTM神经网络层以一种特殊的方式交互,其核心思想是细胞状态[20]。其结构图如图2所示。

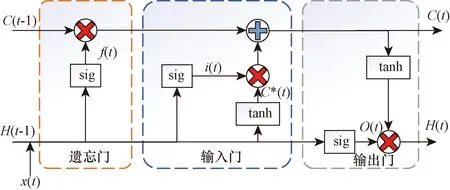
图2 LSTM结构Fig.2 Structure of LSTM

遗忘门f(t)是LSTM工作的第一步,它决定哪些内容从上一个细胞状态中丢弃。遗忘门通过读取上一个细胞状态的输出H(t-1)与当前细胞状态输入x(t),通过sig函数层,对应上一时刻细胞状态的信息C(t-1),决定哪些内容保留,以避免梯度消失与爆炸问题。

输入门通过更新重要信息,即决定哪些新信息保留在细胞状态中。输入门中H(t-1)与x(t)通过sig函数得到输入门i(t)来确定需要保留的值,通过tanh层得到中间细胞状态信息C*(t),并更新细胞状态由C(t-1)到当前细胞状态信息C(t)。

输出门基于细胞状态来确定输出值,H(t-1)与x(t)通过sig函数得到的记忆细胞的输出O(t)来决定哪部分细胞状态需要被输出,而后与C(t) 通过tanh层得到的值相乘,其值作为输出H(t)。各个变量之间的计算公式为

f(t)=sig{Wf[H(t-1),x(t)]+bf}

(2)

i(t)=sig{Wi[H(t-1),x(t)]+bi}

(3)

C*(t)=tanh{Wc[H(t-1),x(t)]+bc}

(4)

C(t)=f(t)C(t-1)+i(t)C*(t)

(5)

O(t)=sig{Wo[H(t-1),x(t)]+bo}

(6)

H(t)=O(t)tanh[C(t)]

(7)

式中:Wf、Wi、Wc、Wo分别为遗忘门、输入门、t时刻细胞状态更新与输出门中各模块对应的权重矩阵;bf、bi、bc、bo为上述各模块偏置项。

单向的LSTM虽具有处理长时间序列的特点,但它只能通过历史数据进行预测。在其基础上,衍生出了双向的LSTM即BiLSTM,BiLSTM具有能够利用历史数据以及未来信息进行预测的能力,参照历史风电数据与未来的天气预报信息,BiLSTM更适合应用于风电预测来推导出风电功率。其结构如图3所示。

BiLSTM神经网络结构模型分为2条LSTM网络,其思想是将同一个输入序列分别接入前向和后向的两个LSTM中,然后将两个网络的隐藏层连在一起,共同接入输出层。

1.2.3 CNN-BiLSTM网络

CNN具有良好的特征提取能力,但随着输入序列的增加,CNN捕获序列之间依赖关系的能力就会变差,而BiLSTM可以综合考虑历史风电数据以及未来天气情况,能够捕获长序列间的依赖性关系,可以很好地克服CNN的不足,因此将CNN与BiLSTM结合起来[21-22]。CNN-BiLSTM结构如图4所示。

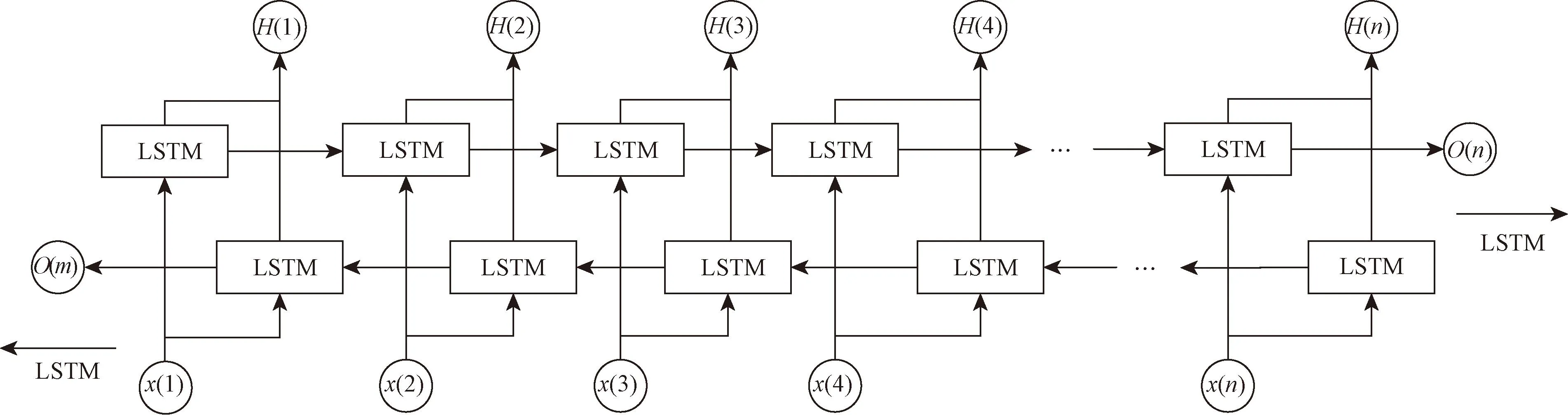
图3 BiLSTM结构图Fig.3 Structure of BiLSTM

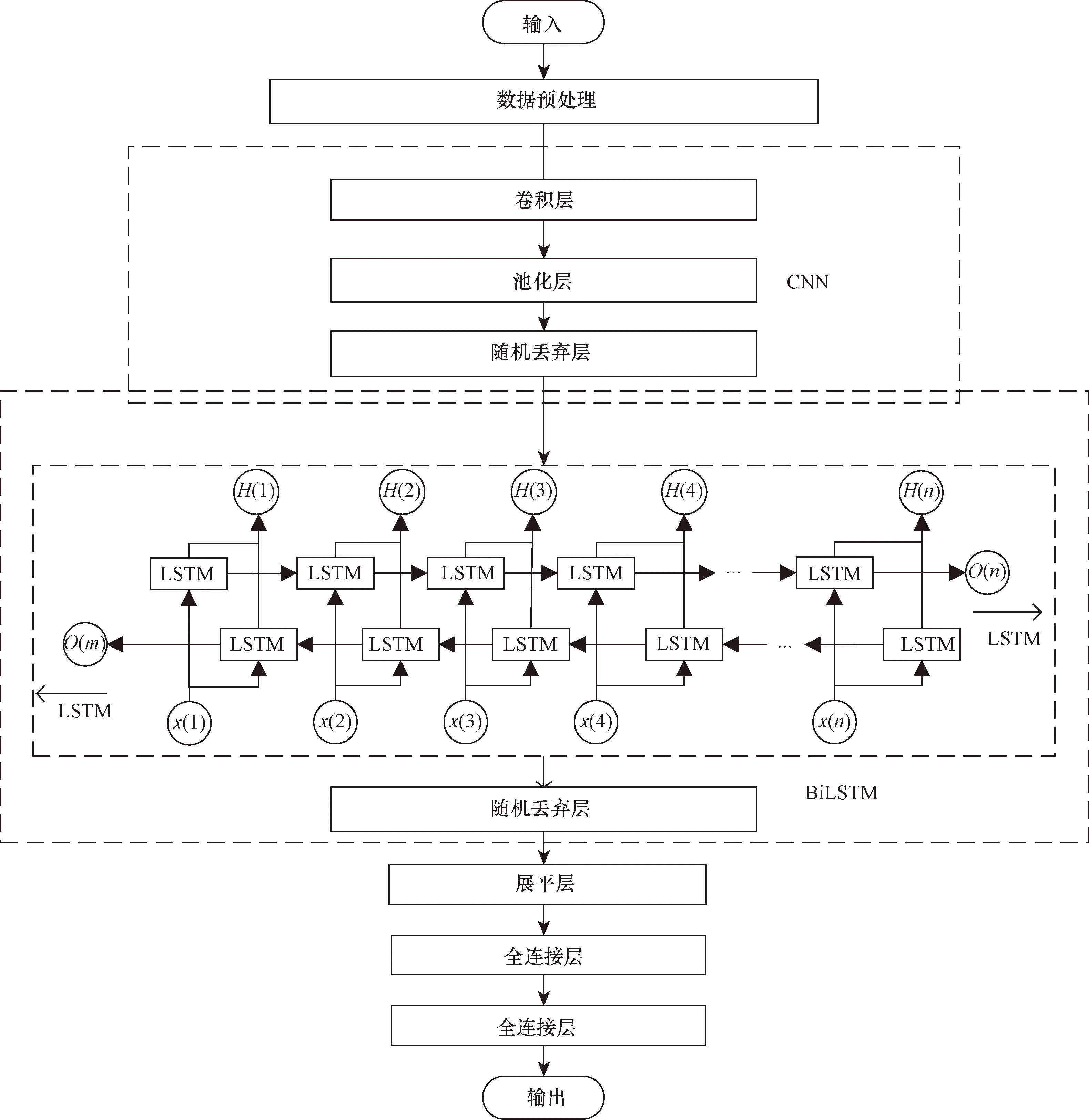
图4 CNN-BiLSTM结构图Fig.4 Structure of CNN-BiLSTM

2 GWO-CNN-BiLSTM模型结构

2.1 GWO原理

灰狼优化算法(GWO)是一种模拟自然界中灰狼的等级制度与狩猎行为的群智能算法。其独特之处在于一小部分拥有绝对话语权的灰狼带领一群灰狼向猎物前进[23]。在一个狼群中,灰狼分为α、β、δ和ω四个等级,上级灰狼对下级灰狼有绝对支配权,如图5所示。

图5 灰狼等级图Fig.5 Gray wolf level chart

第一层:α层狼群。狼群领导者——优化算法最优解。

第二层:β层狼群。狼群次领导者,协助α层狼群——优化算法次优解。

第三层:δ层狼群。服从α和β的决策——适应度差的α和β会降为δ。

第四层:ω层狼群。负责执行上级决策,围绕α、β和δ进行位置更新。

优化过程分为包围、追捕和攻击三个阶段。在GWO中,灰狼包围阶段位置更新为

X(t+1)=XP(t+1)-AD

(8)

D=|CXP(t)-X(t)|

(9)

A=2ar1-a

(10)

C=2r2

(11)

式中:X表示灰狼位置;t为迭代次数;X(t+1)表示以猎物为参考更新后的灰狼位置;XP表示猎物位置;D为灰狼与猎物的距离向量;r1与r2是在[0,1]内随机数;A和C为向量系数,A表示模拟灰狼对猎物的攻击,取值受收敛因子a的影响,而a的取值随着迭代次数从2到0线性递减。

在追捕过程中,猎物(最优解)位置是未知的,因此在GWO中假设α、β和δ对最优解更为了解与接近。迭代过程中α、β和δ来指引ω移动,从而实现全局最优化,位置更新为

Dα=|C1Xα(t)-X(t)|

(12)

Dβ=|C2Xβ(t)-X(t)|

(13)

Dδ=|C3Xδ(t)-X(t)|

(14)

X1=Xα(t)-A1Dα

(15)

X2=Xβ(t)-A2Dβ

(16)

X3=Xδ(t)-A3Dδ

(17)

式中:X1、X2和X3分别为ω与α、β和δ的距离向量;X(t+1)为ω受α、β和δ影响调整的位置。取平均值,即得

(18)

当猎物停止移动,灰狼通过攻击完成狩猎。在优化过程中,当a的值从2线性下降到0时,A的值也在区间[-a,a]内变化,当A>1时,狼群进行全局搜索,当A<1时,进行局部搜索。

2.2 GWO-CNN-BiLSTM模型

风电功率作为一种时间序列,受到自然风的影响,具有强烈随机性、波动性,为准确预测风电功率,所使用的基于GWO-CNN-BiLSTM的预测模型的流程如图6所示。其主要改进是在传统CNN-BiLSTM模型基础上,将GWO优化模块添加到BiLSTM训练模块中,对学习率、隐藏层神经元个数和正则化参数进行优化,增加数据相关性,增强特征的表现能力,使得后续的CNN-BiLSTM预测模块可以学习到风电特征间更深层次的非线性关系,增强拟合程度,使预测精度更高。

首先风电数据输入CNN模块,CNN在减少空间信息损失的前提下,对输入的数据特征进行提取与降维;其次生成训练集与测试集,在BiLSTM模块中训练,在训练过程中应用GWO模块不断对其网络参数进行优化,得出最优值后完成训练;最后通过测试集输出风电预测功率,建立起风电特征与功率之间的模型,完成基于GWO-CNN-BiLSTM的风电预测。

图6 基于GWO-CNN-BiLSTM的预测模型流程图Fig.6 Flow chart of prediction model based on GWO-CNN-BiLSTM

3 算例分析

3.1 模型设置

以美国爱荷华州艾奥瓦城风力发电场2017年检测数据集进行仿真验证,该数据集间隔时长为5 min,取2—3月部分数据(10 071条),取前9 571条数据用作训练,后500条数据用作测试。数据特征包括该风力发电场风速、风向、温度、气压和湿度,一共5个特征。分别使用CNN、BiLSTM、CNN-BiLSTM以及GWO-CNN-BiLSTM四种模型进行仿真对比,仿真环境为MatlabR2022b,CPU AMD R7 5800H,RAM 16.0GB。

模型参数分别设置为:最大训练次数10、梯度阈值1、全局学习率0.001、在训练过程中选择降低学习率、学习率降低因子0.1、小批量处理大小128、BiLSTM隐藏层层数2,GWO-CNN-BiLSTM模型中选择GWO优化目标为学习率、隐藏层神经元个数和正则化参数,GWO设置狼群数量5、最大迭代次数5。所有模型(CNN、BiLSTM、CNN-BiLSTM、GWO-CNN-BiLSTM)输入均为上述所选5种特征,输出为预测功率。

3.2 性能指标

本算例采用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean squared error,RMSE)与回归评测指标(R2)作为性能指标,计算公式为

(19)

(20)

(21)

3.3 预测结果分析

图7为各模型对测试集数据的预测结果,可以发现GWO-CNN-BiLSTM模型与CNN-BiLSTM在整个预测过程中更加贴近实际功率曲线,且GWO-CNN-BiLSTM的偏离程度更小,更贴切于实际功率。

根据表3中各模型性能指标表明,CNN-BiLSTM模型MAE、RMSE和R2较CNN模型与BiLSTM模型分别下降了与上升了51.50%、47.26%、13.92%与38.86%、30.42%、7.15%;而GWO-CNN-BiLSTM模型MAE、RMSE和R2较CNN模型与BiLSTM模型分别下降了与上升了54.40%、60.25%、18.45%与49.39%、47.56%、11.42%;而GWO-CNN-BiLSTM模型各评价指标较CNN-BiLSTM模型分别上升与下降了17.22%、24.63%与3.97%,预测精度有了明显的提升,充分说明了在本文中GWO-CNN-BiLSTM模型相较于其他模型的优越性。

图7 各模型预测结果Fig.7 Prediction results of various models

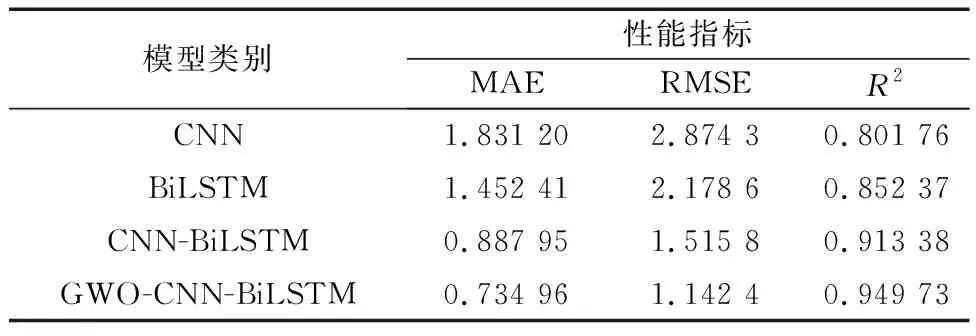
表3 各模型预测性能指标Table 3 Prediction performance indicators of each model

3.4 较长时间风况剧烈波动场景分析

在3.3节中已经分析了在风电预测中采用GWO-CNN-BiLSTM模型的有效性和优越性,但以上分析是基于一般风况情况下。当风电场在某一段时间内因气象等因素存在风况变化剧烈且波动时间较长时,如何对此时的风电功率进行准确预测是一大重点问题。为体现本文GWO-CNN-BiLSTM模型的剧烈风况适应性,选取风电场历史数据中功率变化剧烈的一段,时间间隔为5 min,共1 539条测试数据,分别选取上文预测特性良好的CNN-BiLSTM模型与GWO-CNN-BiLSTM模型在功率变化剧烈阶段进行预测分析对比,验证两种模型的鲁棒性。为使预测结果更为精确,调整相应模型的参数设置。其中CNN-BiLSTM模型在此阶段的功率预测图如图8所示。

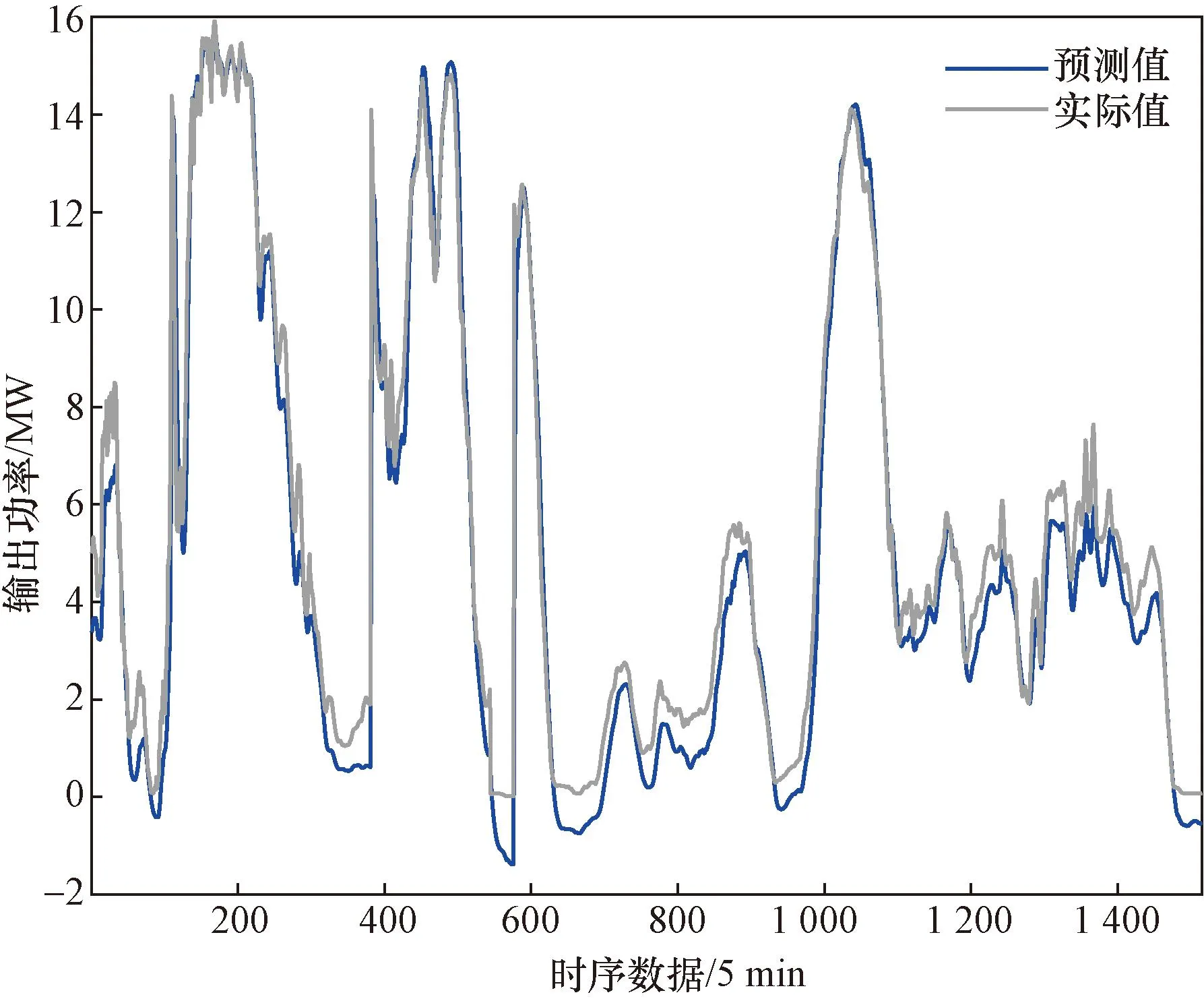
图8 风况波动剧烈时段CNN-BiLSTM模型预测结果图Fig.8 The prediction results of CNN-BiLSTM model in the period of severe wind fluctuation

由图8可以看出,CNN-BiLSTM模型在风况波动剧烈的场景下,功率较大阶段,例如时序数据为0～50与 250～300的时间序列,变化幅度比较缓慢,适应实际输出功率快速变化的能力较差,且预测值在功率高峰期均与实际功率有出入;而在实际功率快速下降阶段,如时序数据为700～850与1 200～1 400的时间序列,预测功率变化虽比较频繁,但跟踪效果不是特别好,预测值与实际值差别较大,变化趋势也不是特别吻合;在风电实际功率接近0的阶段,甚至出现了预测功率为负值的情况,且波动幅度较大。

如图9所示为同等风况条件下采用GWO-CNN-BiLSTM模型预测图。由图9可以清楚地看出,GWO-CNN-BiLSTM模型更贴近实际风电输出功率曲线,在功率较大阶段,例如时序数据为150～250与450～500的时间序列,变化幅度较大,且均未超出实际功率,曲线更为贴合;而在实际功率快速下降阶段,如时序数据为250～300的时间序列,几乎准确地吻合了实际输出功率曲线,误差比较小,其他低功率阶段精度也较高;在风电功率接近0的阶段,采用GWO-CNN-BiLSTM模型的预测功率比实际功率稍偏小,同样出现负值的情况,但波动幅度较小。

两张预测模型性能指标对比可以参照表4,通过表4可以发现,在这个预测集中,GWO-CNN-BiLSTM模型的MAE、RMSE、和R2较CNN-BiLSTM模型分别上升与下降了20.60%、7.51%与0.2%。在风况波动较为剧烈的这一阶段,在加入GWO优化学习率、隐藏层神经元个数与正则化参数前提下,GWO-CNN-BiLSTM模型能够更好地对波动性作出应对,较CNN-BiLSTM模型做出更为精准的风电功率预测。

分析其原因在于,当风况变化剧烈时,除却与预测精度关联性最高的风速特征外,风向、温度、气压以及湿度等弱关联性特征也会出现幅度较大的波动。如果预测模型与弱关联性特征不能建立稳固的联系,在特征发生较大波动时,势必会对模型的预测精度有影响,从而导致预测值的偏差。综上所述,本文所提出的GWO-CNN-BiLSTM模型通过GWO优化了训练过程中的参数,动态地跟随风况数据进行预测,增强了特征的表现力,使预测模型能够更好地挖掘到不同特征间的隐藏联系,尤其实现了对弱关联特征间的关系的精确提取,提高了风电预测的精度。

4 结论

充分考虑了风电预测过程中的不同特征与预测功率的关联性,如温度、风向等弱关联性特征的影响,提出了基于GWO-CNN-BiLSTM的短期风电功率预测方法,通过仿真验证了以下结论。

(1)将具有良好的数据特征提取能力的CNN模型与良好时序特性的BiLSTM模型结合起来,充分考虑风电的特性,CNN-BiLSTM模型比CNN模型与BiLSTM模型更能把控风电特征,预测精度也较CNN模型与BiLSTM模型分别提高了47.26%与30.42%。

(2)考虑风电历史数据中不同特征对预测功率的影响程度,加入GWO优化模型进行训练,可以有效地提高预测模型对非线性特征以及深层次弱关联性特征的学习能力,更精准地把控风电特征与预测值的隐藏关系,将预测模型的精度较没有GWO算法加入前提高了7.51%。

(3)在较长时间风况剧烈波动阶段,不仅强关联性特征波动较大,弱关联性特征也有较为剧烈的波动,由于GWO-CNN-BiLSTM模型的更强学习能力以及对数据的更深入挖掘能力,使得模型能够敏锐地跟踪风电特征的快速变化,对风电功率的预测更为精准。