基于多学科交叉融合的数学建模案例设计与分析
钱龙霞, 王正新, 束 慧
(南京邮电大学 理学院,南京 210023)
0 引 言
随着我国社会经济发展与科学技术进步,数学科学迅速进入了经济、环境、大气、海洋、水文、军事等领域,产生了大量交叉学科,为数学建模开拓了许多新兴研究方向[1-4].数学建模包括初等模型、简单的优化模型、数学规划模型、微分方程模型、差分模型、离散模型、统计模型等,教材为每种模型设置了很多的教学案例,这些案例虽然来自不同领域,但是与实际应用需求联系不紧密, 学生参与课堂讨论的积极性不高[5].在多学科交叉融合背景下,以实际应用需求为牵引,如何设计教学案例吸引学生眼球,充分发挥学生的自主学习能力和科研创新能力,具有重要的现实意义.
目前,很多研究设计了贴近生活和实际应用需求的数学建模案例,如文献[6]在数学建模教学过程中引入了几类经典经济模型案例;文献[7]基于Minitab软件设计了控制图优化的应用案例;文献[8]将“GPS定位问题”引入数学建模的教学中,取得较好的效果;文献[9]探讨了数学建模案例教学的新模式,指出案例收集的重要性和紧迫性.上述数模案例研究中虽然考虑了应用需求,但是没有将不同模型进行综合集成.
规划和多属性评估决策是数学建模中的重点内容,传统教学往往分开讲解,所选案例与实际应用需求以及建模大赛题目相脱节,无法有效培养学生的建模能力.因此,本文以海洋水文保障为背景,以海洋环境对船舶的影响评估与航迹规划为主题设计应用案例,将评估模型与规划模型进行综合集成,试图使学生轻松掌握评估模型和规划模型的数学原理、算法流程和应用前景,培养学生的科研探索能力和创新思维.通过教学实践发现,学生参与课堂讨论的积极性有了很大提高,课堂互动气氛热烈.为了进一步培养学生的科研能力,根据科研项目的需求设置了航迹规划的课后拓展题,发现提交拓展作业的学生人数有了明显的增加,有一名同学解决了变速航迹规划问题并申请了国家发明专利.
综上,本文的创新点为:以科研项目的实际需求为牵引,将数学建模中评估模型和规划模型应用到海洋环境对船舶的风险评估与航迹规划中,设计多学科交叉融合的综合集成教学案例,激发学生参与课堂互动讨论的热情,提升课堂教学效果,提高学生的建模能力和科研能力.需要指出的是,该案例对学生的数学基础、自学能力和算法编写能力要求较高,对于基础一般的同学难度较大,在后续教学中需要进一步优化.
1 应用案例设计
1.1 案例背景
本案例来自海洋水文保障相关科研项目,定量评估气象、海洋水文条件对船舶航行安全的影响并给出相应的辅助决策建议是海洋水文保障的重点内容.影响船舶航行安全的因素有很多,包括海表面波高、海表面温度、海表面盐度、海表面经向流速及纬向流速,如何构建航迹规划模型使得舰船能够避开中高风险区域?基本思路是先对海洋环境风险进行定量评估,在此基础上设计航迹规划算法.假定研究区域范围为110~121°E,15~25°N,共收集了10天的海洋环境要素数据,每天的实测数据分辨率为1/12×1/12,形成较大的133×121的二维数据面.
1.2 建模流程设计
1.2.1 海洋环境风险评估流程
模糊综合评价方法对样本量要求不高,通过构建隶属函数建立每个评价指标与定性评价语言的映射关系,基于加权平均原则进行综合评价.在应用于海况风险评估时,本质上是对现有指标的各个样本信息进行总结,确定每个指标与风险等级之间的隶属函数,根据加权平均原则判定风险等级.模糊综合评价能较好地解决具有模糊不确定性、难以量化的问题,算法原理与建模步骤如下:
(i) 建立综合评价指标体系.评价指标体系为影响评价对象的因素组成的集合,记为U.对海表面波高、海表面温度、海表面盐度、海表面经向流速及纬向流速五个原始指标进行筛选,由于海表面盐度主要是影响海洋设备的受腐蚀速度,总的来说各海域盐度差异不大,其带来的腐蚀速度的差距也很小,可以忽略;对经向和纬向流速进行矢量合成得到海表面流速,最终得到海表面波高、温度以及流速三个指标(图1).
(ii) 确定船舶航行安全风险等级.海洋环境对船舶航行安全带来了不利影响,这种影响可以用风险等级进行度量,船舶航行安全风险等级V可以分为:低风险、较低风险、中风险、较高风险、高风险.
(iii) 确定每个指标与风险等级之间的映射关系,建立模糊综合评价矩阵Rm×n.若评价指标集U中第i个指标属于V中第j个风险等级的隶属度为rij,其中i=1,2,3;j=1,2,3,4,5,则第i个评价指标属于每个风险等级的隶属程度可以表示为Ri=(ri1,ri2,ri3,ri4,ri5),i=1,2,3.因此,所有评价指标属于每个风险等级的隶属程度可以用矩阵R3×5进行表示.常用的隶属度函数有高斯隶属函数、钟型隶属函数、梯形隶属函数和三角形隶属函数等.由于只有10天的样本资料,高斯隶属函数比梯形、三角形隶属函数等更平滑,能刻画小样本的更多信息,结果更可靠[10].综上,本文拟构建高斯隶属函数求解隶属度,表达式如下:
(1)
其中,x为输入的指标样本,σ,c为待估参数,c一般取划分等级区间的中间值,σ常根据指标的灵敏程度进行取值,一般在0.5到1之间.函数f(x;σ,c)代表隶属指标属于某个风险等级的程度,其值越大表示隶属某个风险等级的程度越大.
根据表1划分的各指标等级,波高是效益型指标,值越大风险意味着越大;海水表层流速亦为效益型指标;温度为区间型指标,在区间[18,25]中代表风险最小,从该区间向左右两侧扩散时,风险逐渐变大.不同性质的指标选择的隶属函数不同,且隶属函数的参数也不同.
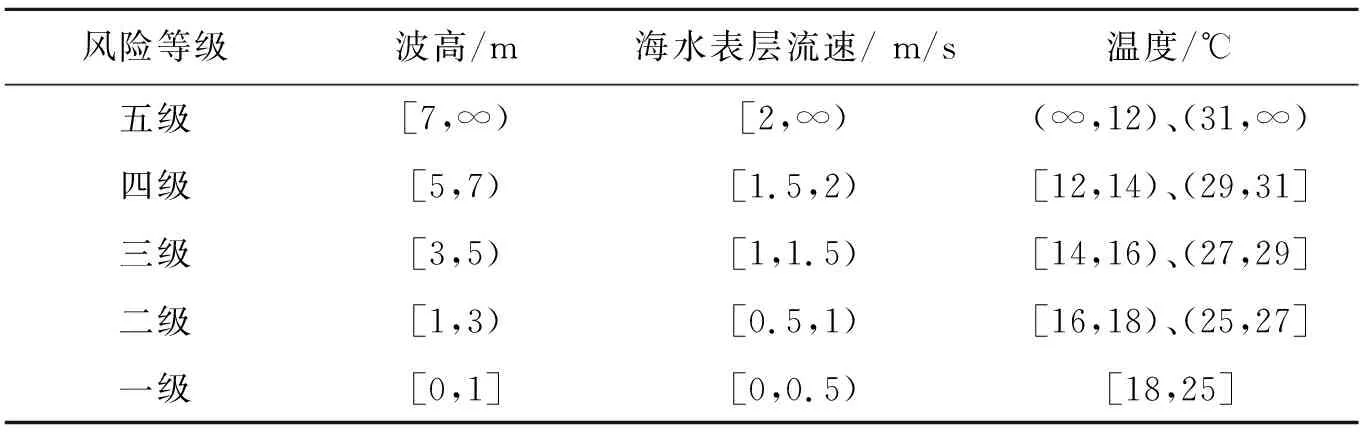
表1 各指标的风险等级标准划分
(iv) 确定指标集的权向量.本文采用模糊层次分析法,该方法能够刻画不同专家在构造比较判断矩阵时的主观不确定性,采用三角模糊数代替传统层次分析法中的标度打分,可以消除标度打分的缺陷.
(v) 进行综合评价.通过线性加权模型将模糊评价矩阵R3×5和权重向量A进行综合,根据得到的模糊向量结果E判断评价对象的风险等级.
E=AR3×5=(e1,e2,e3,e4,e5),
(2)
通过找到上述模糊向量E中最大分量所在下标,再对应到评语集V“低风险、较低风险、中风险、较高风险、高风险”的下标位置上,即可得到该海域某天的风险等级.
1.2.2 航迹规划建模流程
(i) 栅格地图建模
栅格法通过构建二维稀疏矩阵进行数据的存储,矩阵中每个元素的取值为0或1,其中数值1表示障碍物,数值0表示可活动区域.栅格地图及其二值化处理结果如图2 所示.

图2 栅格化地图(左)、二值化地图(右)模型示意
(ii) Dijkstra 算法原理
Dijkstra 算法路径规划基本思路为:为每个节点j创建一组信息j(dj,pj,fj);其中dj为地图中源点到s0当前节点j的最短路径长度(某节点与自身距离为 0);pj为源点s0到节点j的最短距离中到达节点j的前一节点;fj记录节点j的位置信息中dj值是否为空.首先需要定义距离代价,上下移动和左右移动一格,代表海里变化的计算公式如下:
(3)
其中(x1,y1)和(x2,y2)分别代表两格的经纬度坐标,R为地球平均半径.
其次,需要对风险代价进行规范化处理,即将风险值映射到距离代价上,也就是风险值与每次移动的距离最大值的乘积,即斜对角方向移动一格代表的海里数d.
最后,需要定义移动代价函数.为了实现风险最小化和距离最小化,可以通过建立如下的移动代价函数
cost(x,y)=(1-α)×d×fengxian(x,y)+α×[d,Lx,Ly] .
(4)
上式中α和1-α分别为风险代价和距离代价的权重,fengxian(x,y)代表坐标点(x,y)区域的日风险值,[d,Lx,Ly]代表选择三种移动距离之一,分别代表上下移动、左右移动或者斜对角移动.
(iii) 航迹规划算法流程
第一步,确定规划海域.依据任务要求提取海域经纬度信息、地形信息及其分辨率,构建栅格地图,设其为维度m×n矩阵的field.
第二步,海上地形风险评估.对提取到的地形数据进行加工、提炼得到地形风险矩阵Rg,维度为m×n.
第三步,海洋环境风险评估.将1.2.1节得到的风险评估值进行归一化处理,并进行栅格化处理,得到维度为m×n×d的风险矩阵Rf.
第四步,确定约束条件、起始点startPos=(x1,y1)、目标点goalPos=(x2,y2).约束条件主要针对航速进行设定,主要是对每日最大航速v进行设置.
第五步,变速航迹规划算法的实现.利用Dijkstra 算法进行航迹规划,给出合理路线,并在此基础上完成路线在时间维度上的规划.
1.3 案例结果分析
1.3.1 风险评估结果
将该海域10日海况数据代入到风险评估模型中,即可得到10天的海洋环境风险区划结果,如图3-5所示.

图3 第1至第4天的海洋环境风险区划结果
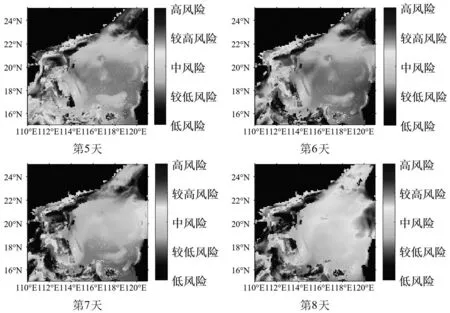
图4 第5至第8天的海洋环境风险区划结果
由图3-图5所示,该海域在前8天,并没有较高风险和高风险的区域.所以,前8天该海域适合航行、风险较低.第9天和第10天该海域存在局部高风险区域,航行时需要避开高风险区域.通过与文献[11]进行比对,发现本文评估结果与该海域过去风险情况基本吻合.

图5 第9天和第10天的海洋环境风险区划结果
1.3.2 航迹规划结果
基于研究海域的栅格地图和风险矩阵,将风险代价权重设置为0.8,即可得到10天的动态航迹规划结果,如图6-图8所示.根据图6-图8可以避开影响舰船航行的险要地形、恶劣气候和人工障碍等不利因素,当海洋环境要素发生改变时,能够及时规划出新的航行路径.
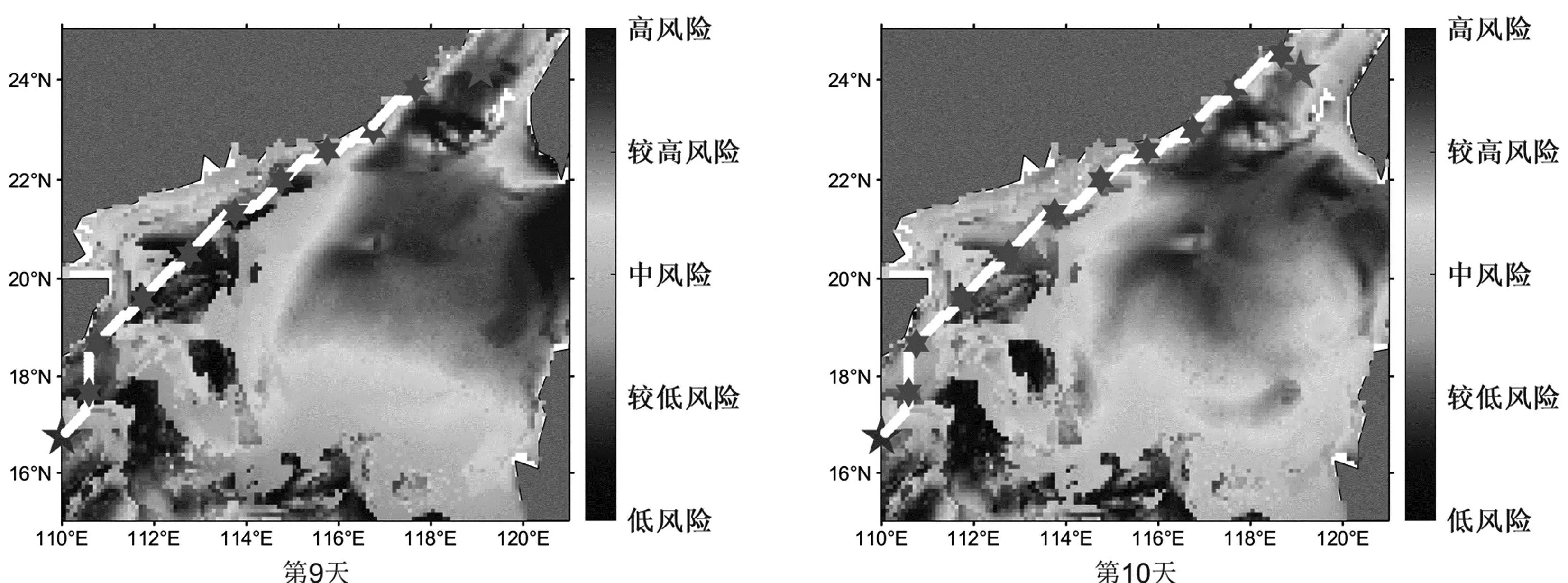
图8 第9天和第10天的航迹规划结果
2 教学效果
上述风险评估与航迹规划案例只是数学建模教学中的一个缩影,针对其它教学内容也设计了基于多学科交叉融合的综合集成案例.为了证明多学科交叉融合的教学案例的效果,在所带班级中选择两个班(A班和B班)进行对比,A班采用多学科交叉融合的综合集成案例,B班采用传统的教学案例,将从两个班提交拓展作业人数(拓展作业是选做题)、平均互动次数、大作业成绩、参加建模人数比例等方面分析综合集成案例引入教学过程的效果,如表2所示.此外,在A班开展了数模课程对于建模能力培养效果的调查,参与调查的人数为123人,调查分析结果如表3所示.

表2 引入多学科交叉融合教学案例的效果对比

表3 建模能力提升效果调查分析结果
由表2可知,采用多学科交叉融合的综合集成案例后,拓展作业提交次数、平均互动次数、大作业平均分以及参加建模人数比例均有了大幅度的提高,说明学生的学习积极性和主观能动性得到明显提升,参与数模大赛的比例达到了69.8%.由表3可知,通过设计紧跟科研项目需求的综合集成案例后,98.4%同学认为自己的建模能力得到有效提高.
3 结 论
本文以海洋水文保障为背景,以海洋环境对船舶的影响评估与航迹规划为主题设计应用案例,将评估模型与规划模型进行综合集成,能够得到动态的航线设计结果.引入多学科交叉融合的综合集成案例后学生的拓展作业提交次数、平均互动次数、大作业平均分以及参加建模人数比例均有了大幅度的提高,有效培养了学生的建模能力和科研能力.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

