高桩码头裂缝张开位移安全监测模型
孙鹏伟
(中交第四航务工程勘察设计院有限公司,广东 广州 510000)
1 XFEM的研究进展
传统的有限元方法(CFEM)在模拟裂缝结构方面存在缺陷,裂缝扩展的不确定性使计算变得更加困难,并且在网格划分时需要更长的时间。扩展有限元方法(XFEM)继承了CFEM的所有优点,单元分解法的采用保证了XFEM的收敛性。它增加了位移场中反映裂缝表面的不连续函数和反映局部特征的渐进位移场函数并反映了裂缝的存在,使裂缝和有限元模型相互独立,克服了高应力高密度网格和裂缝尖端变形集中区造成的困难,它通常被认为是裂缝处理中最有效的数值分析方法。
1.1 国外XFEM的研究进展
XFEM理论最早由美国西北大学教授Belyschko于1999年提出。这是一种新的有限元方法,可以有效地解决不连续力学问题。由于其在分析不连续性方面的独特优势,得到了迅速的发展,并被应用于各个行业和领域。自问世以来,许多学者对该方法进行了改进和完善,着重在断裂问题上,特别是以下几个方面:(1)提高了裂缝尖端场的精度。将XFEM和SAR相结合,分析了分支函数和增强范围对裂缝尖端场精度的影响,提高了裂缝尖端场的精度。(2)数值结果的稳定性和收敛性。为了避免刚度矩阵的奇异性,切割了一些部分来加强节点的自由度,以消除矩阵的奇异性。成功地将标准高斯积分应用于具有裂缝的非连续细胞,并且这些细胞不需要划分为亚基。(3)对应力强度因子计算方法的改进。提出了一种无需后处理即可应用扩展有限元直接计算应力强度系数的方法。该方法不仅考虑了裂缝渐进位移场,还考虑了高阶项。然而,这种直接计算应力强度因子的方法不便于模拟裂缝扩展,仅适用于静态裂缝的应力强度系数计算。(4)裂缝界面的描述和跟踪方法的改进。将水平集方法应用于裂缝界面的说明,并将其与扩展有限元思想相结合,分析更复杂的裂缝界面问题。使用快速行进方法和XFEM来模拟多个裂缝的扩展路径。结果表明该方法效果良好[1]。
1.2 国内XFEM的研究进展
XFEM在国外得到了迅速的发展和广泛的应用,但国内对这一问题的讨论很少。河海大学针对混凝土开裂和破坏分析中现有数值方法的不足,以及XFEM分析不连续性问题的独特优势,利用XFEM对混凝土结构中的裂缝和裂缝扩展进行了数值模拟和分析。使用四节点等周单元建立了I型裂缝黏弹性位移场的数值解格式,为黏弹性断裂问题的位移场分析提供了一种新的方法,建立了闭合摩擦裂缝的扩展有限元模型。模型考虑了裂缝面之间的摩擦接触问题,同时将XFEM和线性互补方法相结合,为解决接触问题开辟了一条新途径。其他学者给出了一种直接计算应力强度因子的扩展有限元方法。该方法无需后处理即可直接计算应力强度因子,大大简化了预处理和后处理[2]。
2 XFEM的特点
XFEM主要采用独立网格的思路来解决无限元裂缝扩展问题,克服了CFEM要求裂缝表面和单元边界一致,裂缝扩展后需要重新划分网格的缺点。扩展有限元方法的特点如下。
(1)XFEM是基于单元分解概念对传统有限元方法进行的扩展。
(2)通过增加位移方程的自由度,实现单元中不连续性的存在。
(3)XFEM不需要重新啮合脆性材料,是一种积极有效的方法,可用于模拟离散裂缝在任何路径上的萌生和扩展。
(4)允许材料非线性和结构几何非线性。
(5)XFEM也可以用于圈出任何静态表面裂缝的线。
(6)允许裂缝表面具有基于小规模滑移方程的接触效应。
(7)XFEM仅适用于一阶应力或位移固体连续单元。
(8)不需要中断网格匹配几何体[3]。
3 材料构成
3.1 钢结构
钢筋的本构关系是通过拉伸试验来测量的,通常使用未经处理的钢筋。目前,最常用的钢筋本构模型包括四种类型:理想弹塑性模型、线性增强弹塑性建模(双线模型)、双重弹塑性模型和理想塑性硬化塑性模型,如图1所示。结果表明,这两种典型的钢本构模型被更多地采用。在本次的数值模拟中,初步建立了理想的弹塑性模型。
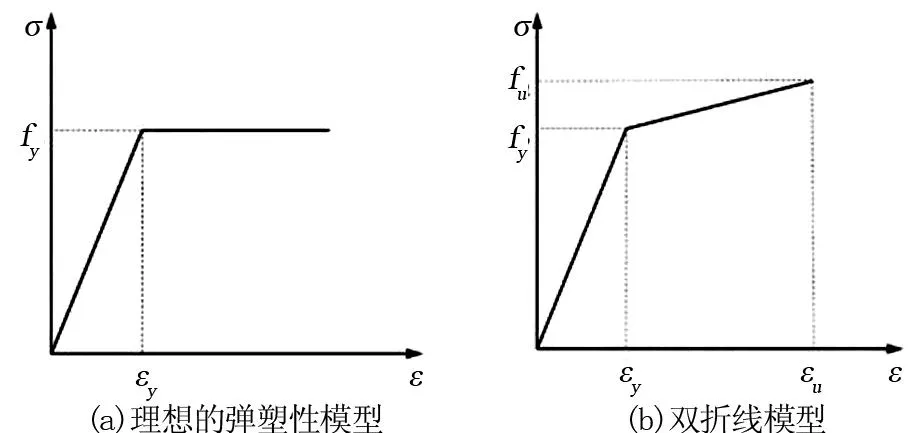
图1 常用的钢筋本构模型
当材料流动阶段较长、结构应变较小、强化阶段可忽略不计时,可以使用理想的弹塑性模型。应力σ和应变ε之间的关系如下。
(1)
(2)
式中:E为弹性模量;λ是一个参数;sign在数学中被称为符号函数。
3.2 混凝土结构
根据《混凝土结构设计规范》(GB 50010—2010)确定混凝土的双轴拉伸本构关系,见公式(3)。
σ=(1-d1)Ecε,
(3)
式中:dt为混凝土的单轴拉伸损伤演化参数;αt为混凝土单轴拉伸应力-应变曲线下降段的参数值;ft,r为混凝土的单向拉伸强度值,实际值需要根据结构进行分析;εt,r为对应于单轴抗拉强度代表值f的混凝土的峰值拉伸应变[4]。
4 实例分析
4.1 工程概况
高桩码头全长162 m,宽14 m。引桥全长66 m,宽10 m。码头采用高桩梁板结构,桩基采用550 mm×550 mm空心方柱,分为斜桩和直桩两种。现浇梁预埋在承台内,梁上布置预制桁条、预制面板和铺筑层。引桥桩基采用预应力空心方柱,桩顶采用1 000 mm×1 000 mm承台,桩间采用纵横梁。承台顶部采用立柱,立柱上采用现浇帽梁,面板采用预制面板,面板上铺设铺筑层。纵梁和前梁位于水位变化区。由于码头已经使用,出现了不同尺寸的裂缝。因此,设置了测缝仪来监测裂缝。考虑到建立裂缝模型的传统方法的局限性,使用XFEM来模拟裂缝的扩展。
4.2 纵梁扩展有限元模型
选取高桩码头前纵梁为模型,纵梁与码头岸线平行布置,码头平台总长162 m,纵梁分为36跨。考虑货架宽度后,相邻横向的纵梁长度计算为4.0 m。纵梁的几何尺寸如图2所示,截面顶面宽度为0.75 m,底部宽度为0.45 m,高度为1.30 m。
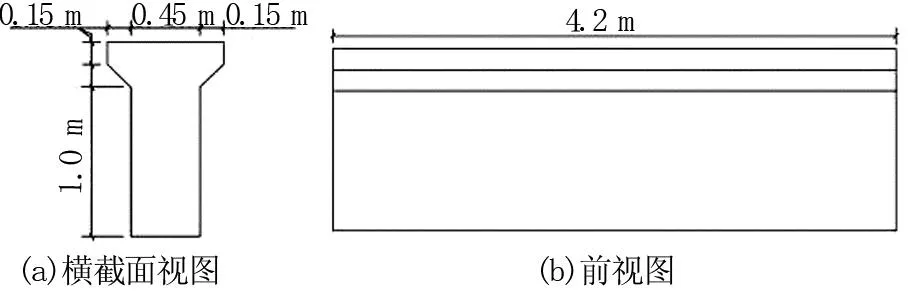
图2 纵梁的几何尺寸
分析中使用的混凝土材料参数:杨氏模量为E=3 000 MPa,泊松比为v=0.167,f=3.19 MPa,黏性区为线性软化本构,断裂能为G=50 N/m,线性膨胀系数为a=10。在纵梁底部的1/4处预埋钢筋,钢筋为HRB400热轧带肋钢筋,直径d=20 mm,弹性模量E=200 GPa,泊松比v=0.3,钢筋密度ρ=7 850 kg/m3。钢筋和混凝土之间采用约束。由于在实际的码头结构中,初始裂缝是在距离一侧的纵向拉伸区末端1.65 m处产生的,因此裂缝在此处重置。初始裂缝贯穿纵梁底部,宽度为0.45 mm,浅层深度为2 mm。在该模型中,纵梁被视为弹性支撑连续梁,选择弹性支撑进行弹性地基和边界设置,刚度系数设置为K=4 000 000 kN/m,建立了现有裂缝的纵向梁模型。网格大小:加密位置为25,未加密位置为50,分为30 576个单元和34 850个节点。钢筋的网格尺寸为10。
在使用期间,梁的自重影响较小。根据分析,得出码头冬季降温期裂缝扩展的主要影响因素是温度骤降。结合实测温度数据,选取了10月至次年1月的降温段,起始温度21 ℃,0 ℃为最低温度。冷却过程设置为多个加载步骤,分别计算每个步骤的温度场。以每个温度场为负载,逐步将温度场应用于纵梁上,以分析整个冷却期码头结构裂缝的开裂过程。
4.3 计算结果
通过计算,得到钢筋混凝土纵梁的最大主应力、应变和变形轮廓。可知纵梁的主裂缝沿初始裂缝方向扩展,而最大主拉应力位于裂缝尖端,并出现明显的应力集中现象。从梁的表面来看,裂缝的扩展路径与梁的高度方向近似水平,裂缝的膨胀方向与主拉应力方向近似平行,初始裂缝则位于构件内部,可以更好地模拟裂缝尖端应力场的奇异性[5]。
图3为裂缝开口值随时间变化图。比较图3中的两条线,可以发现,在10月至次年1月期间,由纵向梁开裂的XFEM模拟引起的裂缝开口值的变化与实际测量的裂缝开口值变化接近,收敛定律基本相同。这验证了XFEM模块在计算裂缝问题时的准确性和方便性。同时,测量值和计算结果并不完全一致,这是因为只考虑了温度对桥墩桁条开裂的影响,并且模型中只嵌入了一根钢筋。在高桩码头的实际施工和使用过程中,它还会受到各种复杂的内部和外部因素的影响,暂时没能作出进一步的分析。例如,堆放荷载等也会导致裂缝的形成。
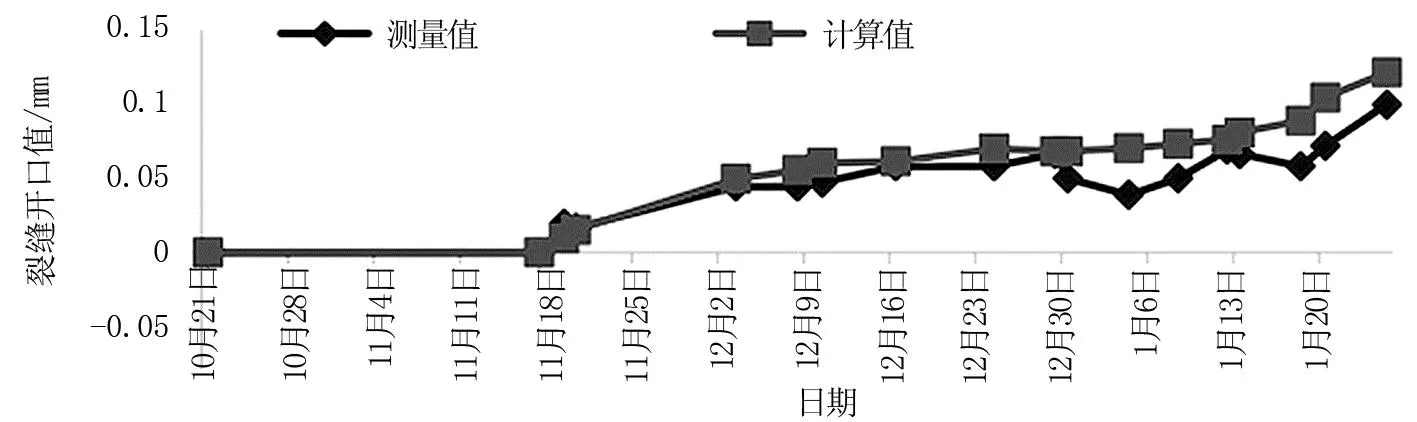
图3 裂缝开口值随时间变化
5 结束语
在模拟过程中,XFEM对网格密度的计算结果影响很小,如果使用传统的有限元方法,则需在裂缝尖端周围布置密集网格以获得良好的结果。由于网格的大小不应设置得太小,当网格尺寸接近0.1 mm时,裂缝不会扩展并出现收敛误差。当网格尺寸接近0.5 mm时,裂缝会扩展,即网格尺寸会影响结果。因此,对于塑性裂缝的扩展,XFEM也存在一些缺陷,需要进行改进。在模拟纵梁开裂的过程中,只考虑了温度下降因素,这显然与码头的正常工作环境不匹配,因此,计算的裂缝张开值与测量数据有所不同。

