桥梁设计阶段基于多目标模糊优化法的工程造价对比分析
徐新帅
(广东省交通规划设计研究院集团股份有限公司,广东 广州 510620)
在桥梁设计阶段,工程造价对比分析是一个关键的环节。通过对不同设计方案的工程造价进行对比,可以帮助工程师选择最优的设计方案,以达到经济效益和设计目标的平衡。然而,在实际工程中,设计目标往往涉及多个方面,如成本、施工时间、结构稳定性等[1]。同时,设计变量的选择也会对工程造价产生影响,例如桥梁的跨度、净高、墩高等。因此,单一的目标函数和设计变量无法全面考虑到这些因素,需要采用多目标优化方法来进行综合分析。在多目标模糊优化法中,模糊数学模型被引入,以处理设计目标和设计变量的模糊性。通过模糊集合和隶属函数的描述,可以更好地反映设计目标和设计变量的不确定性和模糊性[2]。选择适当的模糊优化算法是至关重要的,这类算法能够在设计变量的范围内搜索最优解,并考虑到目标函数的模糊性。通过优化计算和对比分析,可以得到一系列不同的设计方案,并根据设计目标的权重进行评价和排序。根据对比分析的结果,工程师可以进行针对性的方案调整和优化,以满足设计目标和经济效益的要求。
1 多目标模糊优化法在桥梁设计阶段的求解步骤
1.1 多目标模糊优化法
在传统的多目标优化中,通常需要明确给定多个目标函数和约束条件,然后通过寻找最优解集合中的非支配解来得到一组最优解[3]。然而,目标函数和约束条件往往存在不确定性或模糊性,无法用确定的数学函数来描述。多目标模糊优化法通过引入模糊集合、模糊逻辑和模糊规则等概念和方法,对多目标优化问题中的模糊性和不确定性进行建模和处理[4]。允许目标函数和约束条件中的模糊程度,以及变量的模糊取值,从而能够灵活地处理多个目标之间的模糊关系。常用的多目标模糊优化算法包括模糊遗传算法、模糊粒子群算法、模糊模拟退火算法等[5]。多目标模糊优化法的应用领域非常广泛,包括工程设计、决策支持、资源分配、供应链管理等。能够在面对具有模糊性和不确定性的多目标优化问题时,灵活地处理目标和约束之间的模糊关系,提供一组模糊最优解或近似最优解,帮助决策者进行多目标决策和方案选择。
1.2 多目标模糊优化法在桥梁设计阶段的求解步骤
(1)在桥梁设计阶段,需要明确设计目标和约束条件,包括桥梁的安全性、可靠性、经济性、美观性等方面的要求,以及与材料、结构、施工等相关的约束条件[6]。
(2)根据设计目标和约束条件,建立模糊多目标优化模型,包括目标函数和约束条件的定义、变量的取值范围和限制条件等。
(3)在模糊优化模型中,需要对涉及到的变量进行模糊化处理,使这些变量成为模糊变量,并建立相应的模糊集合[7]。
(4)根据模糊优化模型,设计相应的模糊优化算法,包括模糊优化函数、模糊约束条件的定义和求解方法等。
(5)通过应用设计的模糊优化算法,求解模糊多目标优化问题,得到一组模糊最优解或近似最优解[8]。
(6)对求解得到的模糊最优解进行评估,根据设计要求和实际情况,对设计方案进行调整和优化。根据模糊最优解给出的多种方案,进行方案筛选和比较,选择最终的设计方案。
2 基于多目标模糊优化法构建钢箱梁设计模型
桥梁的形式种类较多,以常见的钢箱梁为例进行基于多目标模糊优化法构建设计模型。设桥梁长度为l,钢箱梁横断面示意图如图1所示。
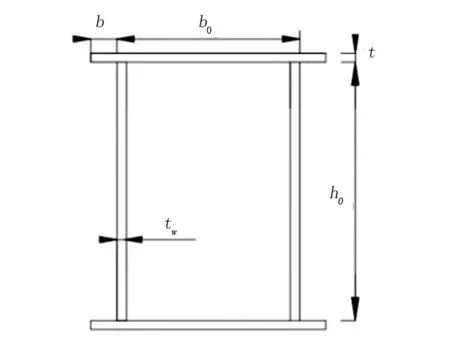
b—钢箱梁翼板外伸的宽度;b0—钢箱梁左右腹板之间的外间距;t—钢箱梁翼缘板的厚度;h0—钢箱梁腹板的高度;tw—钢箱梁腹板的厚度。
使桥梁的各应力、尺寸满足现行规范要求,基于多目标模糊优化法构建钢箱梁设计模型,得到钢箱梁工程造价最低、截面模量最大的方案。
2.1 钢箱梁设计变量确定
钢箱梁的设计变量共有五项,分别为b,b0,t,h0,tw。钢箱梁设计变量集为:
X=(b,b0,t,h0,tw)T
(1)
2.2 钢箱梁目标函数确定
钢箱梁工程造价主要取决于所使用的翼缘板和腹板的造价,工程造价目标函数为
f1(x)=2l((b0+2b)t+h0tw)tR
(2)
式中:R为所用钢材的单位体积价格。
截面模量越大钢箱梁越安全,截面模量目标函数为;
(3)
钢箱梁的目标函数为:
(4)
2.3 钢箱梁模糊约束条件确定
(1)正应力约束条件。
(5)
式中:f表示钢材设计抗弯强度,Mx表示与x轴垂直方向的弯矩,Wnx表示与x轴垂直方向的截面模量。
(2)剪应力约束条件。
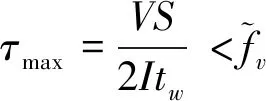
(6)
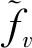
(3)最大静挠度约束条件。
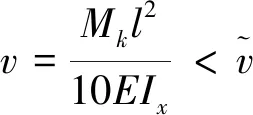
(7)
(4)整体稳定性约束条件。
(8)
式中:fy表示钢材的屈服强度,l1表示受压时钢箱梁翼缘的长度。
(5)翼缘板宽厚比约束条件。
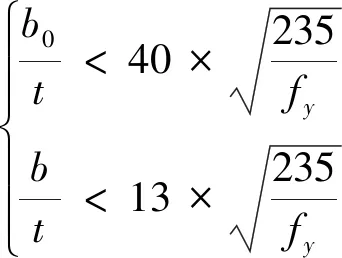
(9)
(6)变量上下限约束条件。
①b约束条件
(10)
②b0约束条件
(11)
③t约束条件
(12)
④h0约束条件
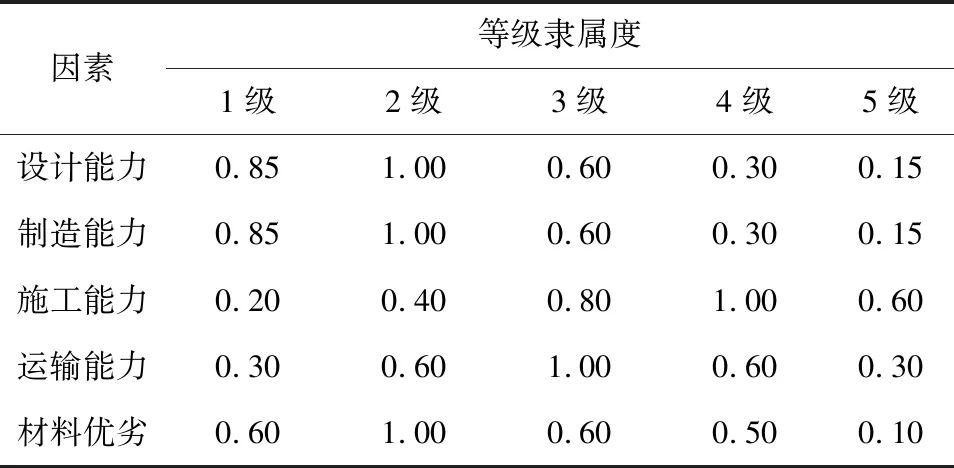
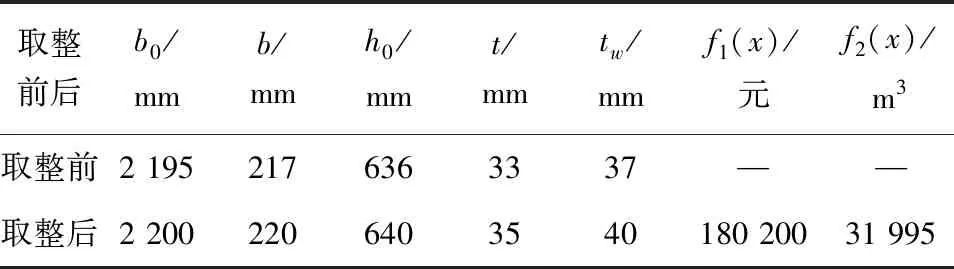
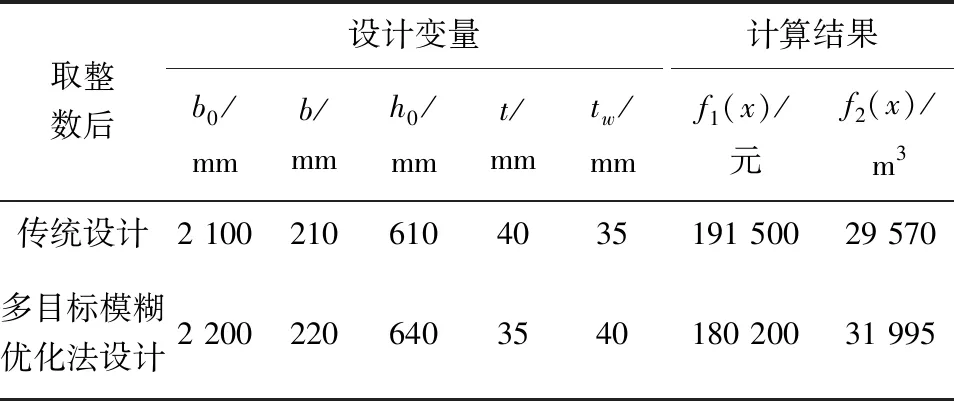
hmin (13) ⑤tw约束条件 (14) 式中:Vmax表示钢材的最大剪切力,fv表示设计的模糊抗剪强度。 公式(1)~公式(12)共同构成钢箱梁设计模型。 江苏省常州市武进区南大街街道计划修建一座天桥,受到资金、政策等方面要求,设计为钢箱梁,环境类别为1类,安全等级为2级,建造所用钢材为Q345耐候钢,计算得到的荷载等级为23.2 kN/m2,该钢箱梁的设计跨径为20 m,计算得到跨径为19.6 m。 (1)计算最优水平值。 使用二级模糊综合评判法,考虑设计、制造、施工、运输的能力和选用材料的优劣五方面模糊因素,将各因素分为5个等级,构建备选集B=(0.6,0.7,0.8,0.9,1.0)。建立评判因素集U=(U1,U2,U3,U4,U5),钢箱梁因素等级隶属度如表1所示。 表1 钢箱梁因素等级隶属度表 对因素等级权重集和评判矩阵求解之后,首先进行一级模糊综合评判矩阵的创建,求得一级模糊综合评判因素权重集E=(0.4,0.25,0.2,0.1,0.05)。随后建立二级模糊综合评判矩阵并计算得到Y=(0.199,0.437,0.757,0.862,0.587),最终得到最优水平值λ=0.449 2。 (2)模糊目标集构建。 根据基于多目标模糊优化法构建钢箱梁设计模型中钢箱梁模糊条件计算公式,使用功效函数法确定各模糊约束的上下限取值,其中将满意值作为上限取值,将不允许值作为下限取值。模糊约束区间的上下限取值见表2。 表2 模糊约束区间上、下限取值 根据最优水平值λ,将模糊约束区间进行实数域集合转化: Gjλ={g|μGj(g)≥0.449 2},j=1,2,…,5 (15) (3)隶属函数构建。 在约束条件下,各目标函数的最大值和最小值分别为 Mj=maxfi(x),mj=minfi(x),其中,i=1,2 得到M1=27 400元,m1=14 900元, M2=41 000 m3,m2=23 950 m3。 (16) (4)全域最优解求解。 该目标函数为非凸函数,使用遗传算法进行全域最优解求解。使用Matlab软件进行编程,将群种大小设为32,交叉概率设为0.95,变异概率取值为(0.01~0.05)。首先进行初始化,然后对群个体的适应度进行求解,之后分别进行交叉计算和变异计算,直至全域最优解出现。 在进行桥梁设计时,将桥梁安全性作为首要目标,其次是桥梁的工程造价。为确定两者所占权重,通过查找相关的规范,并征询相关桥梁设计专家的意见,将权重系数确定为:桥梁安全权重系数ω1为0.6,桥梁造价权重系数ω2为0.4。计算得到的钢箱梁的多目标模糊优化结果见表3。 表3 钢箱梁的多目标模糊优化结果 使用同样的设计参数和工程量进行传统设计,计算所得结果与使用多目标模糊优化法进行设计的计算结果对比如表4所示。 表4 传统设计和多目标模糊优化法设计结果对比 通过表4结果对比,使用多目标模糊优化法设计桥梁比传统设计工程造价能够降低6%以上,同时桥梁的全截面刚度得到了8%左右的提升。由此可知,使用桥梁设计阶段基于多目标模糊优化法设计桥梁是科学有效的方法,能够提高设计方案的经济性和可行性,为决策者提供更好的决策依据,降低工程造价并提高工程质量。 (1)经济性优化。 多目标模糊优化法可以在考虑其他设计目标的前提下,重点关注桥梁结构的经济性。通过优化设计变量,如材料选择、截面尺寸、构件布置等,可以实现结构材料的最佳利用,降低材料成本,能够使工程造价降低3%以上[9]。 (2)结构安全性保证。 桥梁设计中,结构的安全性是至关重要的目标[10]。多目标模糊优化法可以在满足结构安全性的前提下,通过优化设计变量,如截面形状、截面尺寸、构件布置等,提升桥梁的全截面刚度8%左右,提高结构的安全性,从而减少工程的维护成本和风险,间接降低工程造价[11]。 (3)耐久性和维护成本考虑。 桥梁设计中,耐久性和维护成本也是重要的考虑因素。多目标模糊优化法可以在满足其他设计目标的前提下,优化设计变量,如材料选择、防腐措施、维护方案等,提高桥梁的耐久性和维护性,减少维护成本。 在桥梁设计阶段基于多目标模糊优化法的工程造价对比分析是一个复杂而重要的任务,它可以帮助工程师在设计过程中做出明智的决策,以实现经济高效和设计目标的双赢。需要注意的是,多目标模糊优化法需要考虑到设计目标的权重、设计变量的范围和约束条件等因素。同时,也需要结合工程实际情况和专业知识进行合理解释和决策。因此,在实际应用中,建议与专业工程师和相关领域的专家一起进行研究和讨论,以确保结果的准确性和可靠性。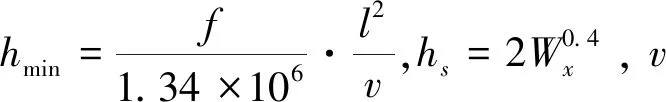
3 钢箱梁多目标迷糊优化法工程造价对比实例
3.1 工程内容
3.2 钢箱梁多目标模糊优化法设计

3.3 传统设计与多目标模糊优化法设计结果对比分析
3.4 多目标模糊优化法对桥梁设计阶段工程造价带来影响
4 结 语

