长细比对五螺箍圆形钢筋混凝土柱轴心受压性能的影响

刘成清，杜成竹，吴宪洪，李广

(西南交通大学 土木工程学院，四川 成都 610031)

在桥梁工程中，柱的截面多为圆形，箍筋通常采用螺旋箍筋；而在房屋建筑工程中，柱多为矩形截面，箍筋通常不采用螺旋箍筋。为了打破传统上螺旋箍筋仅适用于圆形截面柱的限制，翁正强等［1］提出了一种组合式螺旋箍筋——五螺箍，使螺旋箍筋不仅能够应用于矩形截面柱，而且对矩形柱4 个角落的混凝土发挥出良好的约束效果，目前，五螺箍已经在台湾、上海、江苏等地的桥梁工程中得到了应用［2］。

螺旋箍筋的存在使得混凝土处于三向受压的状态，显著提升柱的力学性能。Mander 等［3-4］通过对混凝土柱试件进行轴压试验，指出螺旋箍筋能够提升柱的延性、强度。Abdel 等［5-6］通过对约束混凝土柱进行有限元分析和足尺试验，表明体积配箍率的增加，能够提高柱的轴压承载力和延性。史庆轩等［7］通过对高强箍筋约束高强混凝土试件进行轴压试验，表明体积配箍率对约束混凝土强度和延性提高的影响要大于箍筋强度。张兴虎等［8］对高强螺旋箍筋约束混凝土柱进行抗震性能研究试验，结果表明，在相同轴压比下，其滞回曲线饱满，延性性能较好。翁正强等［1］通过轴压试验，表明采用新型五螺箍矩形钢筋混凝土（reinforced concrete，RC）短柱在箍筋用量的经济效益、抗压强度和韧性上皆优于传统横向箍筋矩形RC 柱。目前，关于螺旋箍筋柱的研究，主要是针对短柱，对中柱、长柱的研究较少，然而长细比对柱承载性能的影响较大，如肖术连等［9-10］通过试验，研究分析了长细比对柱极限承载能力的影响，结果表明，长细比的增大会显著降低构件的极限承载力。在关于长细比对螺旋箍筋柱承载性能的研究方面，刘晓春等［11］运用ANASYS 有限元软件分析长细比对单螺旋箍筋柱轴压性能的影响规律，对其轴压承载力计算公式中稳定系数的取值提出了建议，但未对多螺旋箍筋柱开展相应的研究分析。在《混凝土结构设计规范》［12］中第6.2.16 条给出的钢筋混凝土螺旋箍筋柱的受压承载力计算公式，未定量考虑长细比对螺旋箍筋柱受力性能的影响。由于五螺箍RC 柱优异的力学性能，圆形截面的五螺箍RC柱也能运用到实际工程中，而关于长细比对五螺箍圆形RC 柱轴压性能影响的研究鲜有报道，故研究长细比对五螺箍圆形RC 柱轴压性能的影响具有必要性。

为研究长细比对五螺箍圆形RC 柱轴心受压性能的影响并对其影响进行定量分析，首先，本文基于文献［13］中已有的试验，运用ABAQUS有限元软件建立对应的有限元分析模型，将有限元模型分析结果与已有的试验结果进行比较以验证模型的合理性。然后，在有限元模型经过验证的基础之上，建立具有初始偏心的不同长径比和直径的五螺箍圆形RC柱有限元模型，对其进行轴压荷载作用下的力学性能分析，研究长细比对五螺箍圆形RC 柱轴心受压性能的影响规律；根据有限元分析结果，对五螺箍圆形RC 柱轴压承载力计算公式进行稳定系数的修正及给出稳定系数的取值建议。

1 有限元分析模型建立及验证

1.1 有限元分析模型建立

五螺箍构造方式是由1 个中心大螺箍和4 个角落的小螺箍而组成，三维模型如图1所示。

图1 五螺箍圆形钢筋混凝土柱三维模型Fig.1 Three-dimensional model of five-spiral stirrup for circular reinforced concrete column

五螺箍圆形RC 柱分析模型采用位移协调分离式进行建模，其中，混凝土采用C3D8R 单元，纵筋及螺旋箍筋采用T3D2 单元。根据柱的实际受力情况，柱上下两端面的边界条件采用铰接的连接方式来进行模拟，加载方式采取对柱顶面进行位移加载的模式，同时考虑到螺旋箍筋在受到轴向荷载作用时可能会沿加载方向旋转，因此在加载方向多施加一个转动约束。在轴向荷载作用下，混凝土与钢筋之间的相对滑移较小。为便于建立模型，不考虑混凝土与钢筋之间的相对滑移，采用Embedded Re‐gion的接触关系来耦合两者之间的自由度。在进行位移加载时，为了使端面的力分布趋于均匀，减小应力集中，对加载面采取参考点与端面Coupling关系。

1.2 材料的本构关系

混凝土的本构模型采用ABAQUS 内置混凝土塑性损伤模型，损伤因子的计算采用文献［14］提出的转换公式。通过整理、验算和分析国内外大量钢管混凝土轴压短柱试件的试验结果，在充分考虑钢管对混凝土产生约束效应的基础上，韩林海［15］提出了钢管混凝土中核心混凝土本构模型，故本构关系采用韩林海［15］考虑横向约束效应的核心混凝土本构模型，其本构曲线如图2所示，其具体表达式为：

图2 核心区混凝土本构曲线Fig.2 Stress-strain curve of the core concrete

式中：σ0、ε0分别为约束混凝土峰值应力和峰值应变；β为综合考虑混凝土强度和钢管约束效应的曲线形状控制参数；ξ为约束效应系数；ε为核心区混凝土应变；As为钢管的横截面积；Ac为核心区混凝土的横截面积；fy为钢材屈服强度；fck为混凝土轴心抗压强度标准值。

钢筋的本构模型采用理想弹塑性模型，本构关系曲线如图3所示，其具体表达式为：

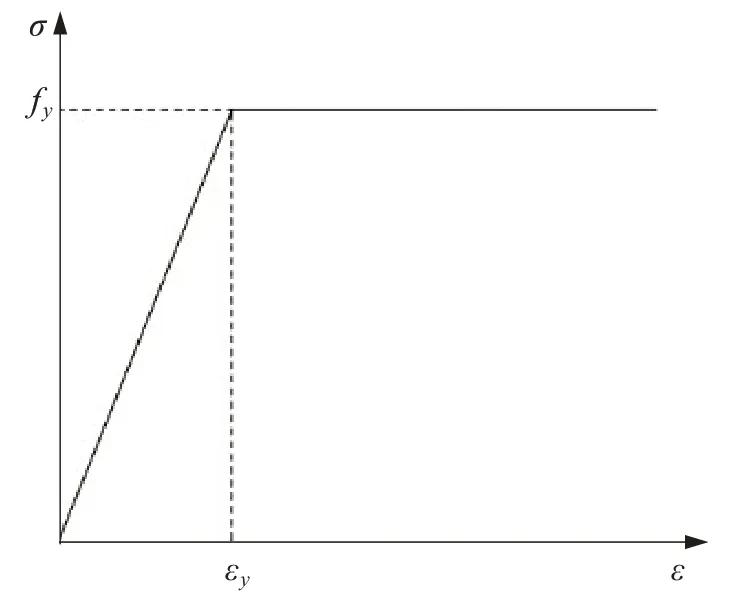
图3 钢筋本构关系曲线Fig.3 Stress-strain curve of steel

式中：Es为钢筋的弹性模量；Fy为钢筋的屈服强度。

1.3 有限元模型验证

为了验证本文模拟方法和所建立的有限元模型的合理性，选取文献［13］中的C2-1、C2-3、C2-4 和C2-5 试件来进行建模分析、比较。图4 中是各试件有限元与试验的应力-应变曲线图。4 根短柱的试验设计参数、有限元和试验结果如表1。

表1 有限元计算分析结果与试验结果比较Table1 Comparison of finite element results and experimental results

图4 有限元与试验应力应变曲线的比较Fig.4 Comparison of finite element simulated and stress-strain curves

根据图4 可以看出，有限元分析计算得到的应力应变曲线与试验结果对应的应力应变曲线吻合较好。从表1 可以发现，轴压承载力的模拟计算结果要略高于试验结果，最小误差为1.17%，最大误差为7.35%，平均误差仅为4.51%，这说明建立的有限元分析模型对模拟五螺箍柱具有合理性。

2 五螺箍圆形RC柱承载性能的影响分析

2.1 参数设定

为进行轴向荷载作用下五螺箍圆形RC 柱的有限元计算分析，在保证纵筋配筋率和体积配箍率基本一致的基础上，建立3组不同直径、不同长径比的五螺箍圆形RC 柱，每一组分为11个构件，每组构件按核心区长径比的大小依次从2 逐渐增加到12，截面配筋布置及尺寸如图5 所示，构件的主要参数如表2所示。

表2 五螺箍圆形RC柱模型构件主要参数Table 2 Main parameters of five-spiral stirrup for circu‐lar reinforced RC columns

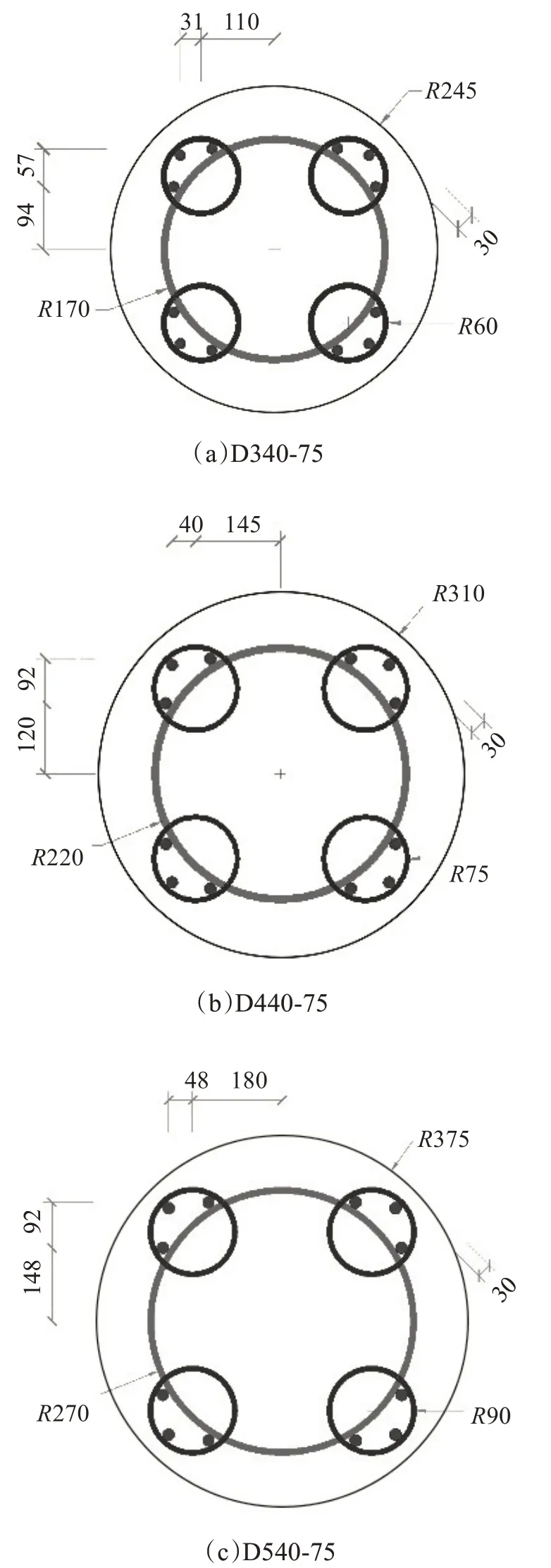
图5 五螺箍圆形RC柱截面配筋布置及尺寸Fig.5 Reinforcement arrangement and size adjustment for section of five-spiral stirrup for circular RC columns

为对比轴向荷载作用下五螺箍圆形RC柱与普通螺箍圆形RC柱的承载力，选取3组长径比为4的五螺箍圆形RC柱作为对照，保证纵筋配筋率、体积配箍率和长径比与五螺箍圆形RC柱相同的基础上，建立3组普通螺箍圆形RC柱。普通螺箍圆形RC柱截面配筋布置及尺寸如图6所示，构件的主要参数如表3所示。

表3 普通螺箍RC柱模型构件主要参数Table 3 Main parameters of spiral stirrup for circular RC columns

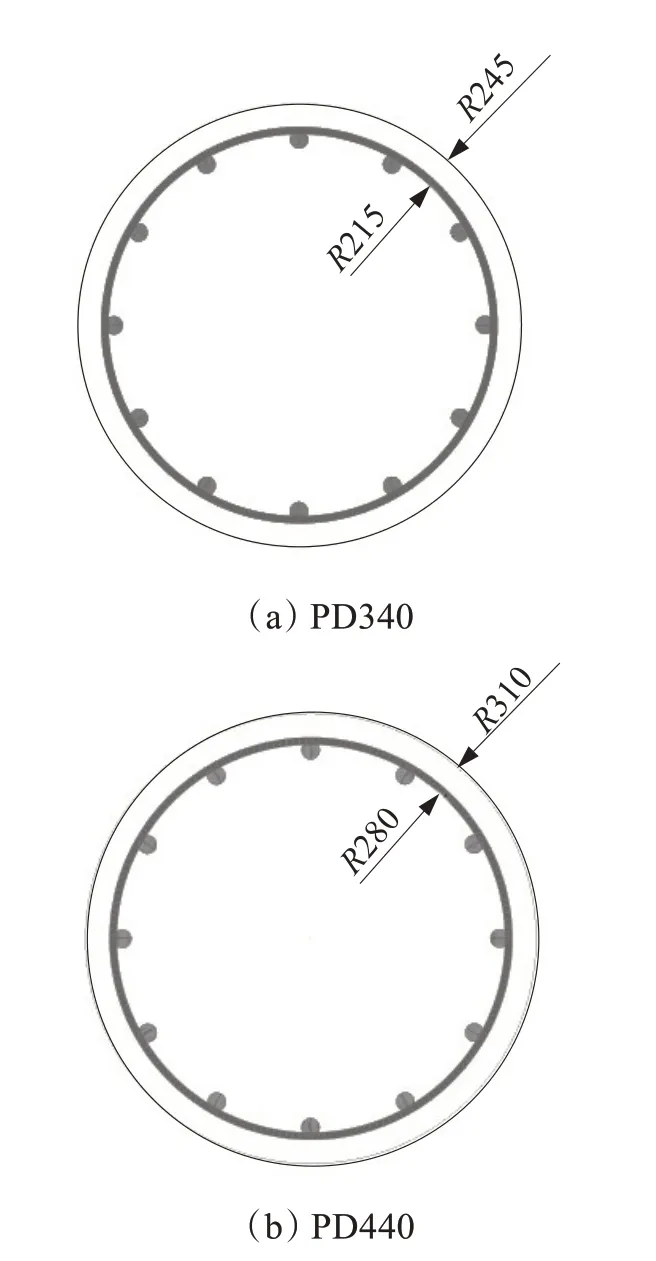
图6 普通螺箍圆形RC柱截面配筋布置及尺寸Fig.6 Reinforcement arrangement and size adjustment for section of spiral stirrup for circular RC columns

为研究不同主次箍直径对荷载-位移曲线的影响，在构件D440-75 的基础上，选取长径均为4的构件，保证长径一致的基础上改变主次箍的直径大小，建立6 组不同主箍直径和次箍直径的五螺箍圆形RC柱，构件的主要参数如表4所示。

表4 不同直径螺箍RC柱模型构件主要参数Table 4 Main parameters of stirrup for circular RC col‐umns with different diameters

五螺箍圆形RC 柱和普通螺箍圆形RC 柱的混凝土强度等级取为C40，纵筋及螺旋箍筋均选取HRB400 级钢筋，其中大螺箍、小螺箍的间距均取为75 mm，考虑到初始偏心对中柱和长柱轴压承载性能的影响，参考文献［15］的模拟方法，对长径比大于2的每个构件施加l0/1 000的初始偏心。

2.2 五螺箍与普通螺箍圆形RC柱承载力对比

图7 为轴向荷载作用下五螺箍圆形RC 柱与普通螺箍圆形RC 柱的承载力的对比。从图7 中可以看出，五螺箍圆形RC 柱的峰值荷载大于普通螺箍圆形RC 柱，五螺箍圆形RC 柱的峰值位移和极限位移均大于普通螺箍圆形RC 柱，极限位移取为0.85倍峰值荷载对应的位移。相比于普通螺箍圆形RC柱，五螺箍圆形RC 柱具有更大的轴压承载力和更好的延性。

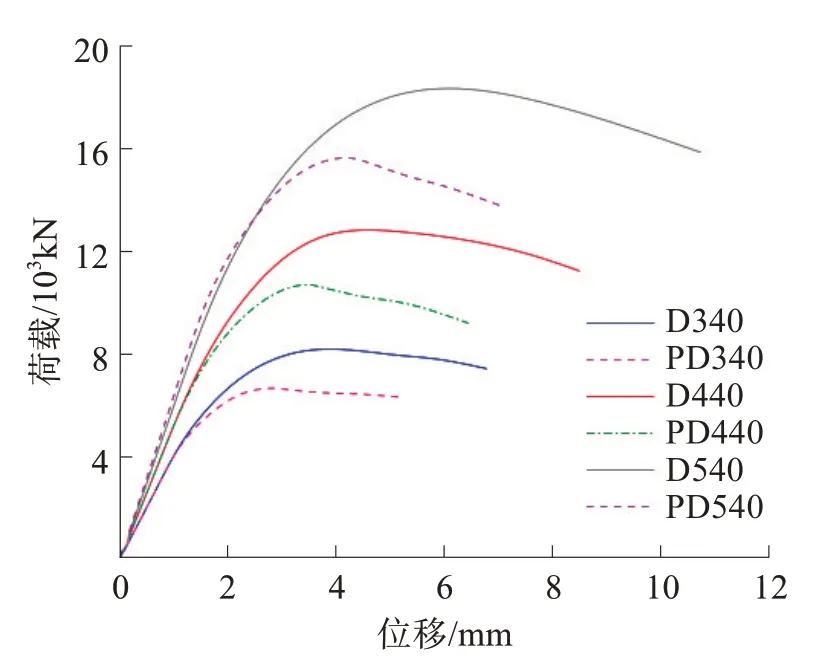
图7 五螺箍与普通螺箍的荷载-位移曲线Fig.7 Load-displacement curves of five-spiral stirrup and spiral stirrup

2.3 主箍直径和次箍直径对荷载-位移曲线的影响

不同主次箍直径对荷载-位移曲线的影响如图8所示。从图8中可以看出，同一主箍直径的五螺箍圆形RC 柱的峰值荷载随着次箍直径的增大而逐渐增大，峰值位移和极限位移在逐渐增大；同一次箍直径的五螺箍圆形RC 柱的峰值荷载随着主箍直径的增大而逐渐增大，峰值位移和极限位移也在逐渐增大。

图8 五螺箍不同主次箍直径的荷载-位移曲线Fig.8 Load-displacement curves of five-spiral stirrup with different primary and secondary stirrup diameters

2.4 长径比对荷载-位移曲线的影响

3组有限元分析模型的荷载-位移曲线随长径比的变化情况如图9所示。从图9可以看到，同一截面的五螺箍圆形RC柱的峰值荷载随着构件长径比的增大而逐渐降低；峰值位移和极限位移在逐渐增大。随着长径比的增大，构件达到峰值荷载以后，曲线下降段的斜率逐渐增加，出现刚度退化现象，这是由于随着长径比的增加，初始偏心引起的附加弯矩的影响和几何非线性以及材料非线性的影响越来越显著，延性降低，破坏时极限应变减小，构件的承载力降低。

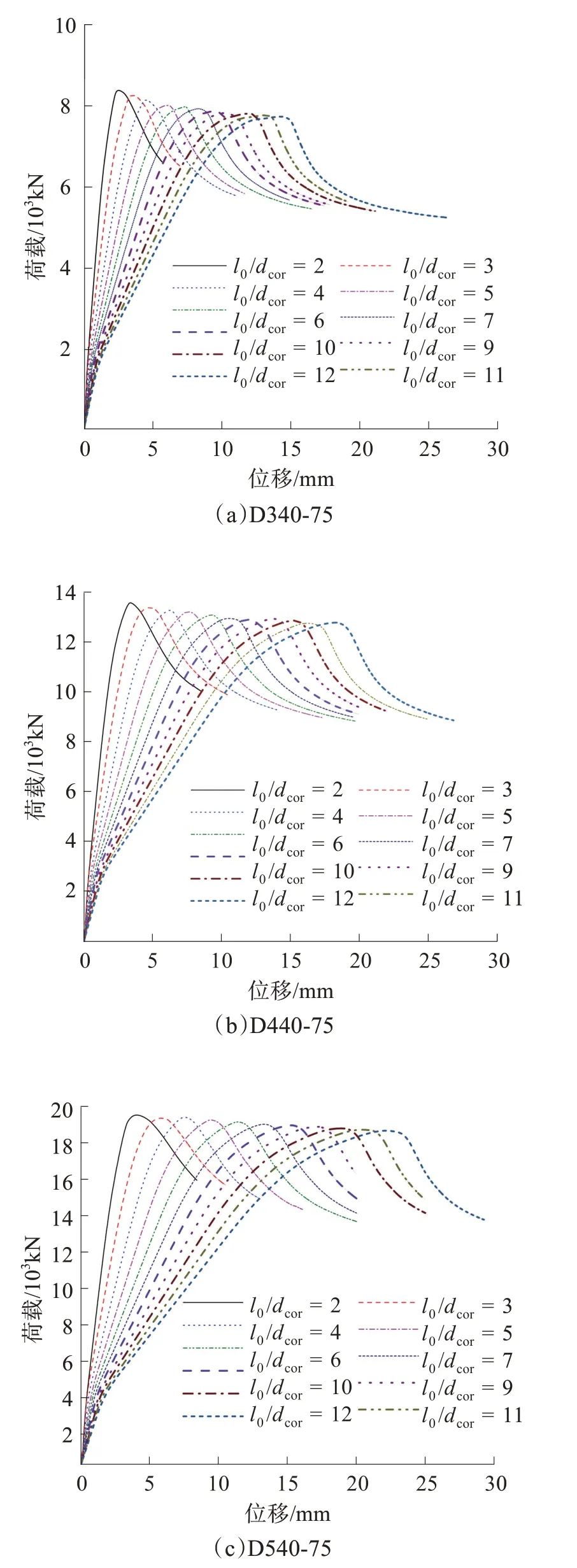
图9 不同长径比的荷载-位移曲线Fig.9 Load-displacement curves with different length-diame‐ter ratios

2.5 长径比对荷载-侧向挠度曲线的影响

图10为不同长径比对荷载-侧向挠度的影响曲线。从图10中可以看出，在荷载加载初期五螺箍圆形RC 柱的侧向挠度与荷载基本上成正比例关系；当加载的荷载达到峰值荷载的75%左右时，随着荷载的逐渐增加，侧向挠度的增长速度加快；当荷载加载到峰值荷载后，构件的侧向挠度急剧增加，承载力逐渐降低。对于同一组构件，长径比越大，构件在相同荷载作用下的侧向挠度就越大，二阶效应对其轴心受压承载性能的影响越显著。

图10 不同长径比的荷载-侧向挠度曲线Fig.10 Load-lateral deflection curves with different length di‐ameter ratios

图11 分别给出了D540-75 组有限元分析模型在长径比分别为2、4、6、8、10 和12 时柱中混凝土的侧向挠度变形图。

图11 D540-75有限元模型部分侧向挠度变形图Fig.11 Lateral deflection diagram of finite element models of the D450-75

从图11 中可以看出，随着长细比的增大，初始偏心引起的二阶效应显著增加，增大了构件的侧向挠度和附加弯矩。

由于受到轴向力和弯矩的共同作用以及二阶效应的影响，五螺箍圆形RC 柱在中部发生破坏，这种破坏会导致柱在初始偏心方向的一侧出现最大的轴向压应力和较大的塑性变形。

2.6 长径比对承载力和稳定系数的影响

图12 为峰值荷载随长细比的变化情况，从整体上可以看出随着长径比的增大，五螺箍圆形RC 柱的承载力呈下降的趋势，但下降较平缓。根据有限元模型的分析结果，计算五螺箍圆形截面RC 柱的稳定系数，其计算结果及轴心受压承载力见表5。取每组构件长径比分别为2和12的构件峰值承载力来计算其下降程度，在D340-75组中，峰值承载力从8 360.02 kN 降低到7 726.4 kN，峰值承载力降低了7.58%；在D440-75组中，峰值承载力从13 555.54 kN降低到12 753.51 kN，峰值载力降低了5.92%；D540-75组中，峰值承载力从19 520.52 kN降低到了18 661.17 kN，峰值承载力降低了4.40%，这说明增加截面面积可以在一定程度上提高柱的抗压承载能力，并减少初始偏心造成的影响。在文献［11］中，3 组单螺旋箍筋轴心受压承载力随长径比增加而下降的程度较为明显，从长径比为2到长径比为12，承载力下降情况为：在dcor=400 mm组中，承载力从5 552.3 kN降低到了4 733.1 kN，承载力降低了14.75%；在dcor=500 mm组中，承载力从8 584.4 kN降低到了7 227.6 kN，承载力降低了15.81%；在dcor=600 mm 组中，承载力从12 364.3 kN 降低到了10 319.6 kN，承载力降低了16.54%。可见，五螺箍圆形RC柱的稳定承载力要高于普通单螺旋箍筋柱，而且增加截面的面积能够降低长径比对峰值承载力的下降程度。

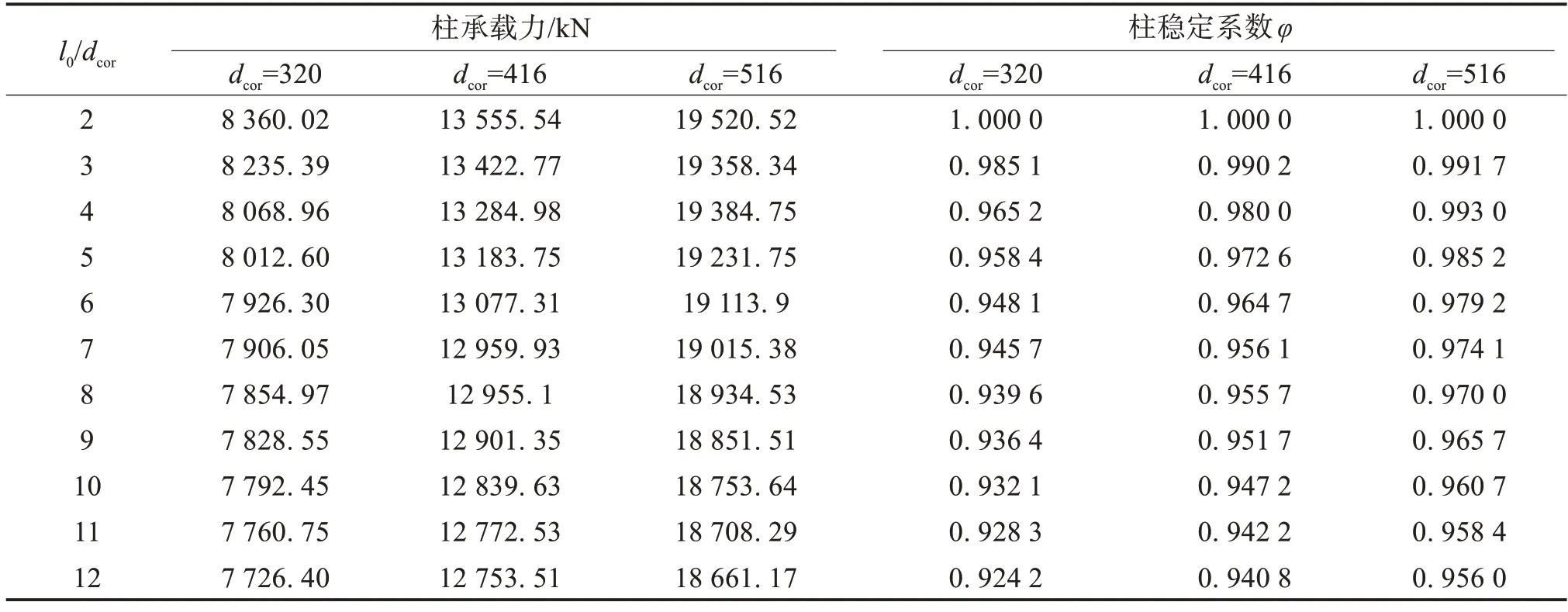
表5 五螺箍圆形截面RC柱的稳定系数Table 5 Stability coefficient of five-spiral stirrup for circular RC column

图12 五螺箍圆形RC柱峰值荷载-长径比曲线Fig.12 Peak load-length diameter ratio curves of five-spi‐ral stirrup for circular RC column

3 组五螺箍圆形RC 柱的稳定系数随长径比变化的关系曲线如图13所示。从图13中可以看到，长径比相同时，随着截面面积的增加，构件的稳定系数有所增大；同一组构件中，随着长径比的增加，五螺箍圆形钢筋混凝土柱的稳定系数逐渐下降，但下降的整体速率要低于参考文献［11］中的单螺旋箍筋柱稳定系数的下降速率，这说明五螺箍圆形RC 柱中4个角落的小螺箍使混凝土处于多向受压状态，提高了承载力的稳定性，使得稳定承载力要优于普通单螺旋箍筋柱。

图13 不同长径比的五螺箍圆形RC柱的稳定系数Fig.13 Stability coefficient of five-spiral stirrup for circu‐lar RC column with different length-diameter ra‐tios

3 五螺箍圆形截面RC柱的稳定系数计算

3.1 螺旋箍筋柱承载力计算的比较

目前国内外有关螺旋箍筋柱承载力计算的主要规范、标准如下：

1）GB 50010-2010［12］中规定螺旋箍筋柱正截面受压承载力的计算公式为：

式中长径比l0/d≤12。

2）JSCE 15：2007［16］中规定螺旋箍筋柱正截面受压承载力的计算公式为：

式中：λ≤35按短柱计算；λ≥35按长柱计算。

3）ACE 318-14［17］中规定螺旋箍筋柱正截面受压承载力的计算公式为：

式中：0.85为影响系数，表示尺寸效应对正截面受压承载力的影响。

目前，国内外规范、标准对螺旋箍筋柱均未考虑长细比对正截面受压承载力的影响。但在实际的建设工程中，钢筋混凝土柱会受到各种不确定因素如施工误差、材料不均匀的影响，使轴心受压柱在初始偏心的影响下柱截面产生附加弯矩。对短柱来说，附加弯矩产生的二阶效应较小，柱的承载性能受到的影响也较小，可不予考虑；在中、长柱中，附加弯矩产生的二阶效应对柱的承载性能影响较大，柱会产生明显的侧向变形，随着长细比的增大，二阶效应的影响更加显著。虽然螺旋箍筋对混凝土提供的约束作用比普通箍筋强，但从表5可知，随着长细比的增大，螺旋箍筋柱的承载力也受到了影响，故应该考虑长细比对螺旋箍筋柱正截面受压承载力的影响。

同时，当前国内外对螺旋箍筋柱正截面受压承载力的计算主要是针对单螺旋箍筋，对多螺旋箍筋柱正截面受压承载力的计算还未规范化，因此为了具体反映出4 个小螺箍对承载力的贡献，参考文献［18］中五螺箍柱的轴压承载力计算公式，并建议在考虑初始偏心影响的基础上，对其进行稳定系数修正，修正公式为：

式中：fc为混凝土轴心抗压设计值；fy为螺旋箍筋抗拉屈服强度；fy'为纵向钢筋的抗压强度；Acor为核心区混凝土面积；A's为纵向钢筋的截面面积；Ac1为大螺箍的有效约束面积；Ac2为小螺箍的有效约束面积；ρv为体积配箍率；s为螺旋箍筋的间距；dcor为核心区混凝土直径。

3.2 五螺箍圆形RC柱稳定系数计算公式修正

为得出考虑初始偏心影响的五螺箍圆形RC 柱的稳定系数φ计算公式，采用Origin 绘图软件对有限元分析计算得到的稳定系数φ与长径比进行拟合。通过对图10 曲线的观察和便于计算的综合考虑，采用二次抛物线多项式对曲线进行拟合，得出了五螺箍圆形RC柱的稳定系数φ计算公式为：

式中核心区长径比l0/dcor≤12的取值范围为2～12。

为验证稳定系数计算公式的拟合效果，对有限元分析计算得出的不同长径比五螺箍圆形RC 柱的稳定系数与利用式（10）进行相应的计算得到的结果进行对比，对比情况如表6所示，有限元分析计算得出的稳定系数与采用式（10）计算得到的稳定系数之间的平均误差为0.22%，两者的结果非常接近，故当五螺箍圆形RC 柱的长径比在2～12 时，稳定系数φ可查表6，当长径比不为整数时可采取线性内插法进行取值，也可按稳定系数计算式（10）进行计算。

表6 五螺箍圆形RC柱稳定系数计算比较Table 6 Comparison of stability coefficient calculation of five-spiral stirrup for circular RC column

4 结论

1）随着长径比的增大，同一组五螺箍圆形RC柱的峰值荷载逐渐降低，峰值位移和极限位移在逐渐增大，五螺箍圆形RC 柱达到峰值荷载以后，荷载-位移曲线下降段的斜率逐渐增加，出现刚度退化现象，承载力降低；随着长径比的增大，五螺箍圆形RC 柱在相同荷载作用下的侧向挠度就越大，二阶效应对其轴心受压承载性能的影响越显著。

2）长径比相同时，随着主次箍直径的增大，五螺箍圆形RC 柱的轴压承载力、峰值位移和极限位移在逐渐增大；随着截面面积的增加，长径比对五螺箍圆形RC 柱承载力下降程度的影响有所降低，五螺箍圆形RC 柱的稳定系数有所增大；同一组构件中，随着长径比的增加，五螺箍圆形RC 柱的稳定系数逐渐下降，下降的整体速率要低于单螺旋箍筋柱稳定系数下降的速率，其稳定承载力要优于普通单螺旋箍筋柱。

3）在总用钢量相同的情况下，对比于普通螺箍圆形RC 柱，五螺箍圆形RC 柱具有更大的轴压承载力和更好的延性。

4）当五螺箍圆形RC 柱的核心区长径比范围为2～12 时，稳定系数φ可查表取值，若核心区长径比不为整数，则可采取线性内插法进行取值，也可按稳定系数计算式进行计算。