GNSS拒止环境下的手机车载定位研究

丁龙阳，旷俭，陈起金，牛小骥

（武汉大学 卫星导航定位技术研究中心，湖北 武汉 430079）

近年来，随着驾车出行方式的普及以及自动驾驶技术的发展，对车载导航定位的需求日益突出。全球卫星导航系统(global navigation satellite sys‐tem,GNSS)在开阔环境下能够全天候地提供高精度定位服务，被广泛应用于车载导航。但是GNSS 在城市峡谷、地下停车场等场景中，会因多路径效应及信号遮挡的影响，导致定位精度下降甚至失效。惯性导航系统(inertial navigation system,INS)具有自主导航的能力，可以为车辆定位提供包括三维位置、速度与姿态在内的完整导航信息，但是其定位误差随时间累积。尤其是低成本微机电系统(micro elec‐tro-mechanical system,MEMS)INS，零偏和噪声大［1］，短时间内位置误差就会迅速积累至无法单独使用。

GNSS/INS 组合可以充分发挥各自的优势，从而提供连续可靠的定位结果，在车载导航中得到了广泛的应用［2-3］。但是当GNSS 信号出现中断时，这种组合方案就会退化成INS 方案，定位误差依然会随时间迅速累积。因此，需要寻求可用的辅助信息或辅助传感器来抑制惯导误差累积。

在很多自动驾驶或高精度车载定位系统中，搭载多种辅助传感器，如里程计［4］、激光雷达［5］、相机［6］、超声波传感器［7］等，通过多传感器数据融合获得较高精度的位置信息。但是，上述专用设备往往价格昂贵、安装复杂，目前难以在大众应用中普及。对一般用户而言，实际驾车过程中往往是靠智能手机来实现车辆定位。智能手机不仅体积小巧、价格低廉，还内置有丰富的传感器，如GNSS 接收机、MEMSIMU、磁力计、相机等［8］，可为车辆导航定位提供所需要的全部观测值。但是智能手机内置的传感器精度都比较低，如何挖掘低精度传感器的性能，在没有GNSS辅助的场景下（例如地下车库）保证位置推算精度成为了研究热点和难点。

利用车辆的运动约束信息，构建虚拟观测，是一种有效的、无额外成本的惯导修正方法。车辆在正常行驶（不发生侧滑和垂向跳跃）的过程中一般满足非完整性运动约束(non-holonomic constraints,NHC)，即车辆只会有前向的速度，横向和垂向速度为零［9］。文献［9-11］利用这一约束显著提高了车辆定位精度。由于NHC无法对前向速度进行约束，文献［12］通过蓝牙接口引入车载诊断系统中的轮速信息，与NHC的横向、垂向零速共同构成完整性约束，从而进一步提高GNSS拒止环境下的定位性能。但是这种方法的缺点在于不同车辆生产商没有提供统一的接口，因此难以普及。文献［13］采用有监督学习方式训练前向速度预测模型，测速误差可以控制在0.5 m/s 以内，但是该方法的缺点在于不同场景下手机的晃动程度差异较大，训练好的模型不具有普适性。此外，车辆可能会偶尔停车，此时可以使用零速修正以及航向角速率修正［14］来有效控制速度误差和航向误差累积。

除了利用车辆自身的运动信息，磁力计常被用于提供航向信息［15-16］。但是车辆外壳主要由铁磁性物质组成，会造成磁干扰使磁航向不可用，因此磁力计在车载导航中的应用受到了较大限制。文献［17］提出的方法可以较好隔绝周围环境的干扰，但是所用传感器十分昂贵。文献［13］将车辆外壳的影响等效为磁零偏进行标定，使用比绝对磁航向更加可靠的磁航向角变化量，构建航向角观测值辅助惯导推算。

本文在没有GNSS 辅助的条件下，研究基于智能手机的车载定位方案在车辆行驶时（不考虑车辆静止）的推算能力。该车载定位方案主要是利用非完整性约束以及手机内置磁力计辅助手机惯导进行推算。本文通过在地下车库这种典型场景中实测了多组数据，研究了如何最大程度发挥NHC 的作用，维持惯导的推算精度，具体讨论了非完整性约束中的安装角和杆臂、磁航向修正在基于手机的车载定位方案中的作用，并尝试为后续的研究指出方向。

1 手机端车载组合定位算法

1.1 算法框架

本文所讨论的算法是在GNSS/INS 组合导航的基础上，使用非完整性约束（NHC）以及磁航向变化来辅助手机MEMSIMU 进行车辆位置推算。在GNSS 信号中断的情况下，该算法就退化为NHC 和磁航向辅助的MEMS惯导的航位推算模式。

图1 给出了基于智能手机的车载组合定位算法的原理流程。首先通过惯导机械编排获得IMU 的位置、速度和姿态。然后在开阔环境下，通过融合GNSS 位置信息可以有效抑制惯导误差累积并使MEMSIMU 的零偏等增广误差至收敛状态；在GNSS 信号中断的场景下（图中虚线框内部分），将INS 推算结果、非完整性约束信息以及磁航向修正信息通过扩展卡尔曼滤波(extended kalman filter,EKF)进行数据融合得到修正后的手机位速姿。

图1 手机端车辆定位算法原理流程Fig.1 Vehicle positioning algorithm flowchart based on smartphones

1.2 系统误差状态模型

为解决系统的非线性问题，带有辅助信息的惯性导航常采用误差状态卡尔曼滤波进行组合导航解算［18］。本文主要采用了15 维和20 维2 种误差状态向量。其中15 维误差状态量包括导航状态向量以及IMU误差向量：

为充分发挥非完整性约束的作用，需要补偿IMU 安装角和NHC 杆臂。因为不补偿IMU 安装角会使得NHC 约束直接作用在IMU 的3个轴向上，而不是车辆的前向、横向和垂向［19］；不补偿NHC 杆臂会使得NHC 约束直接作用在IMU 中心而不是NHC最符合的点上［20］，造成其侧向速度与垂向速度并不为零，这都会影响NHC 的性能从而降低定位精度。其中，IMU 安装角定义为IMU 坐标系（b系）与车辆坐标系（v系）之间因轴系不对正引起的角度差异；NHC 杆臂定义为IMU 测量中心到NHC 约束点（本文具体选在车辆后轮中心）的向量，如图2所示。

图2 IMU安装角和NHC杆臂定义Fig.2 Misalignment angle of IMU and the lever arm of NHC

在实际车辆行驶过程中，手机位置通常不固定而且存在晃动，使得安装角和杆臂会发生变化。因此预先标定好安装角和杆臂，然后直接设定的方式势必会影响NHC性能的发挥，而如果采用在线估计的方式则可以实现自动标定安装角和杆臂，从而缓解上述问题。因此本文将俯仰、航向安装角误差及NHC 杆臂误差（三维）增广到状态向量中进行在线估计，形成20维误差状态向量。完整的20维误差状态向量为：

式中：(δγ)T为俯仰安装角和航向安装角误差（横滚安装角对于NHC 不需要也不可估［19］）；()T为NHC杆臂误差，即IMU 测量中心到车辆后轮中心的杆臂误差。

通过误差扰动分析，可以推导出位置、速度与姿态的误差微分方程，详细的推导过程以及完整的变量描述可参见文献［21］。

陀螺和加速计零偏建模为一阶高斯-马尔可夫过程：

式中：Tbg、Tba分别为陀螺零偏、加速度计零偏的相关时间；wbg、wba分别为陀螺零偏和加速度计零偏的驱动白噪声。

1.3 约束观测模型

1）非完整性约束。

在车辆载体坐标系下，当NHC 成立时，速度观测向量可以表示为：

式中：vforward为车辆沿前进方向的速度；ev为观测噪声，可以根据运动状态初步给定，并通过残差调整。本文所讨论的算法只针对侧向速度和垂向速度进行约束，因此下面的观测方程只取侧向和垂向分量。同时，由IMU 推算的速度投影到载体坐标系下可以表示为：

2）磁航向修正。

本文采用文献［13］提出的方法来发挥磁航向的修正作用。虽然铁磁性的车辆外壳会造成磁干扰，但是这种磁干扰的主要部分可等效为磁力计零偏。通过预先准确标定磁力计零偏并扣除后，基于磁力计观测值得到的磁航向角可以大致反映真实的航向角变化，因此可以利用磁航向角的变化量构建航向角观测值。磁航向的计算方法以及航向角观测值的构建方式如下。

首先根据手机的水平姿态角（即横滚角和俯仰角）将磁力计测量值投影到水平面，然后利用投影后的磁力计水平分量计算磁航向角：

式中：φ、θ分别为手机的横滚角和俯仰角；mx、my和mz为磁力计三轴原始观测值；Mx、My分别为磁力计观测值投影后的水平方向的2 个分量，ψmag为磁航向角。

得到磁航向后，可以使用磁航向角变化量构造航向角观测值，具体观测方程为：

式中：ψins、ψmag分别为惯导机械编排得到的航向角以及磁航向角；k为当前计算历元编号；k0为准静态磁场对应的历元编号；nϕ为航向角观测值的量测噪声。准静态磁场的判定方法可参见文献［22］。

2 定位方案与手机车载实验

根据是否补偿安装角和杆臂、是否在线估计手机IMU 安装角和NHC 杆臂以及是否使用磁航向辅助3个条件，本文共探究了4种在GNSS中断条件下的手机车载定位方案。4 种方案均使用了非完整性约束来抑制惯导误差发散，具体见表1。

表1 无GNSS辅助下基于手机的车载定位方案Table 1 Description of vehicle positioning schemes based on smartphones in GNSS-Denied environments

为评估算法性能，在地下车库场景中进行了车载实验，包含“多转弯型”复杂轨迹和“直线型”轨迹2 种典型轨迹。测试手机型号为HUAWEIMate 40 Pro，通过支架固定在车辆前端中控顶部，如图3 所示。手机记录了MEMSIMU、磁力计、GNSS 单点定位结果等原始数据。手机内置MEMSIMU 型号为ICM-20690。参考系统为迈普时空导航科技有限公司的战术级GNSS/INS 定位定姿系统POS 320 参考位置通过事后动态差分(post processed kinematic,PPK)、INS 与里程计松组合并进行反向平滑处理获得。位置精度可达厘米级到分米级。手机内置MEMS 级别IMU 与POS 320 中战术级别IMU 的主要技术参数见表2。

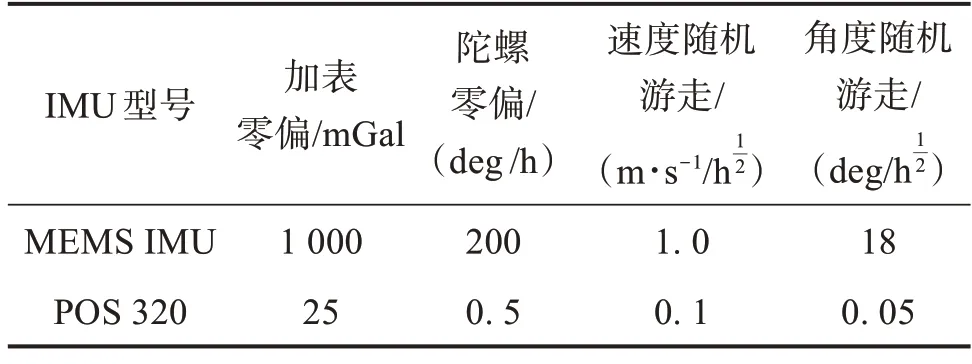
表2 IMU的性能参数Table 2 Performance parameters of the IMUS

图3 手机的安装位置与安装方式Fig.3 Installation position and method of smartphones

本文进行了2 项实验，分别在典型的“多转弯型”地下车库（实验1，见图4（a））和“狭长型”地下车库（实验2，见图4（b））开展测试。每项实验均采集了10 组独立的数据用于精度统计。由于用户关心的是在地下车库中车辆行驶的距离与定位精度的关系，本文以在地下车库中行驶指定距离为前提开展实验。具体地，实验1在地下车库中行驶500 m，其中包括10 个转弯，期间GNSS 信号完全中断，中断时长大约为140 s；实验2 在地下车库中行驶800 m，其中包含一段大约为500 m 的长直线，期间GNSS 信号完全中断，中断总时长大约为280 s 。

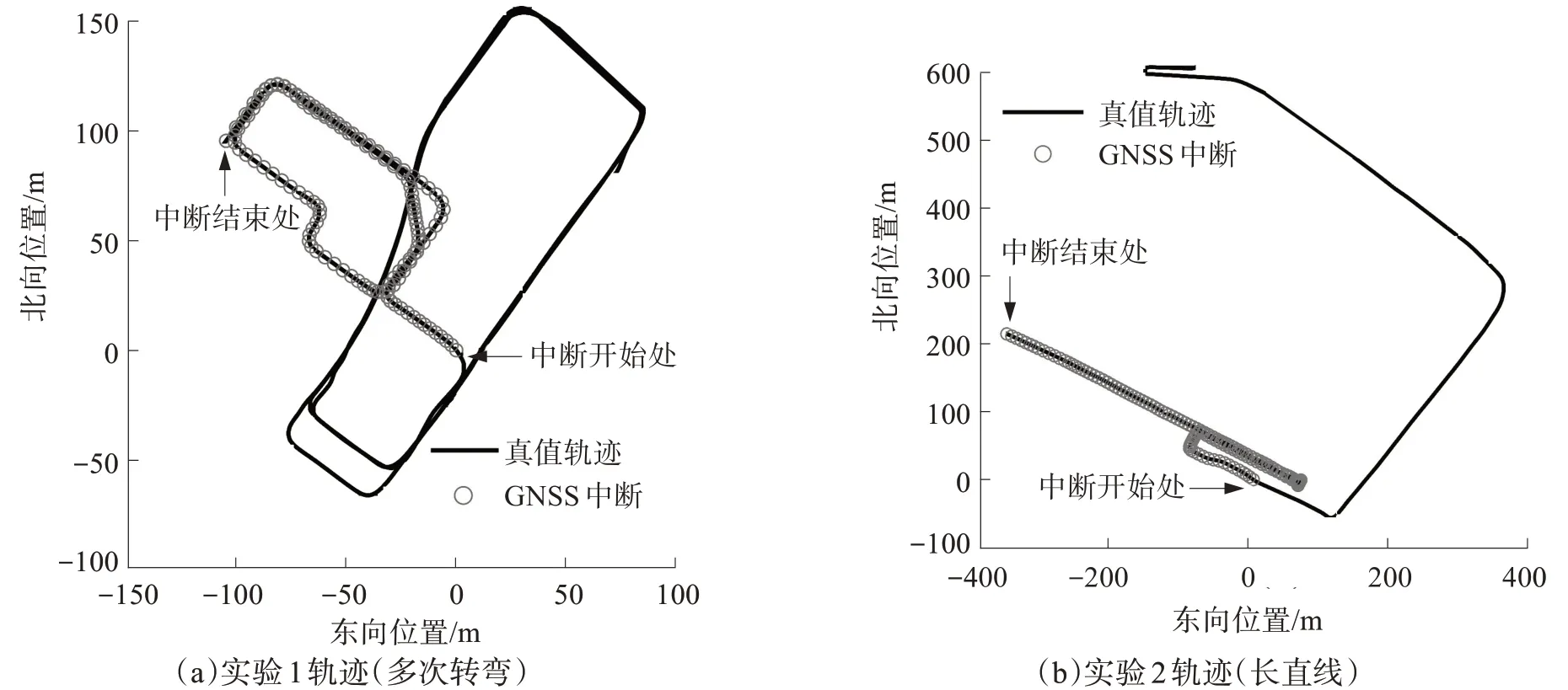
图4 实验轨迹Fig.4 Trajectory of tests

由于手机内置MEMSIMU 性能低(含有较大噪声以及陀螺稳定性差)，若其主要误差不充分收敛，进入地下车库后，定位误差会迅速发散至不可用。因此，本文在进入地下停车场之前（GNSS 中断之前），MEMSIMU 的主要误差均已通过融合GNSS 定位结果充分收敛。每项实验使用10组数据的终点平面位置误差的RMS值作为统计结果，并计算终点平面位置相对测量误差（位置误差与轨迹长度的比值）。实验数据的处理方式均为按照实时模式的离线处理。

3 多转弯和长直线场景定位性能分析

3.1 实验1（多次转弯）

表3 展示了实验1 采集的10 组数据在GNSS 信号中断500 m（时长140 s）后终点平面位置误差的所有结果，表格的最后2 行分别给出了终点平面位置误差以及终点平面位置相对测量误差（位置误差与轨迹长度的比值）的RMS统计值。

表3 实验1中断GNSS信号500 m终点平面位置误差结果Table 3 Error of terminal positionin the case of a 500 m GNSS signal outage (test 1)

从表2 最后的RMS 值可以看到，在直接使用NHC 时（方案1），终点定位误差统计值为16.9 m；当进行安装角和杆臂补偿后（方案2），终点定位误差RMS 统计值迅速减小到8.7 m，精度大约提升了48%。图5 与图6 分别为实验1 中的一组数据在补偿安装角和杆臂前后，载体坐标系下的速度投影图。从图5、6中可以看到，在补偿安装角和杆臂后，与水平位置误差相关的横向速度投影有明显的减小，从而能够更严格地符合NHC 约束，提升定位精度。

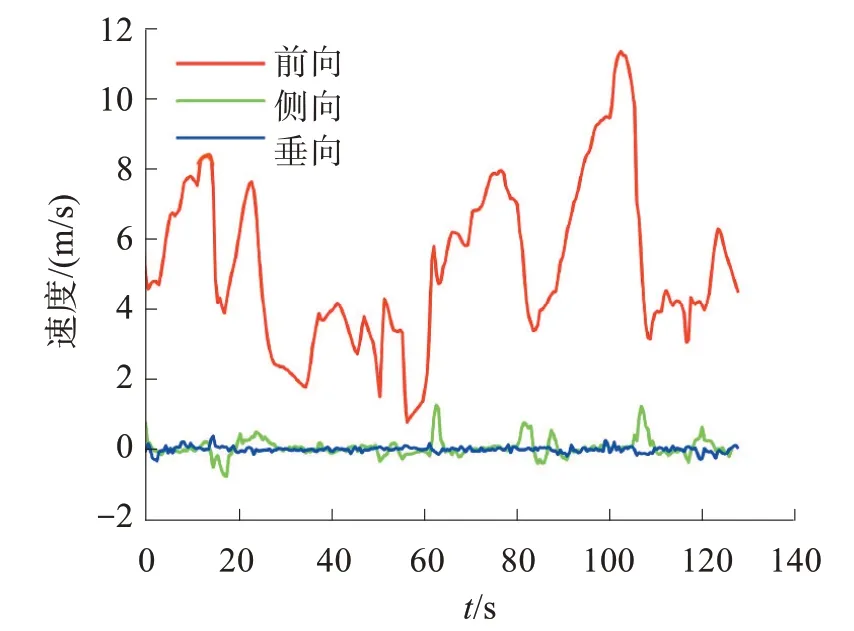
图5 实验1进行IMU安装角和NHC杆臂补偿前的速度投影Fig.5 Velocity in v-frame before compensating the misalign‐ment angle of IMU and the lever arm of NHC（test1）

图6 实验1进行安装角和杆臂补偿后的速度投影Fig.6 Velocity in v-frame after compensating the misalign‐ment angle of IMU and the lever arm of NHC（test1）

将IMU 安装角和NHC 杆臂进行在线估计后（方案3），终点位置误差统计值会进一步减小到8.3 m，相比方案2 略有改善，终点平面位置相对测量误差仅有1.66%。因为在实际车辆行驶过程中，即使手机被固定在支架上，也会因为路况颠簸以及车辆速度的变化导致手机晃动，进而会造成安装角发生变化。在线估计安装角可以更好地应对这一变化，对IMU 安装角进行动态调整，进而更好地发挥出NHC 的性能，提升定位精度。此外，实验1 结果显示加入磁航向修正前后位置精度差异不大。这一方面因为相比长直线轨迹，实验1 多转弯轨迹中相同航向误差引起的位置误差更小；另一方面因为实验1 频繁的转弯动作，使得NHC 能够有效修正速度误差，并进一步修正航向误差，使航向误差较小，因此磁航向修正难以起到显著作用。

图7 是实验1 中一组典型数据4 种定位方案的轨迹推算结果对比。从图7 中不难看出，相比于方案1，方案2、3、4 的推算轨迹明显更加贴近参考真值，这主要是因为经过IMU 安装角和NHC 杆臂补偿后能够更加准确充分地使用NHC。

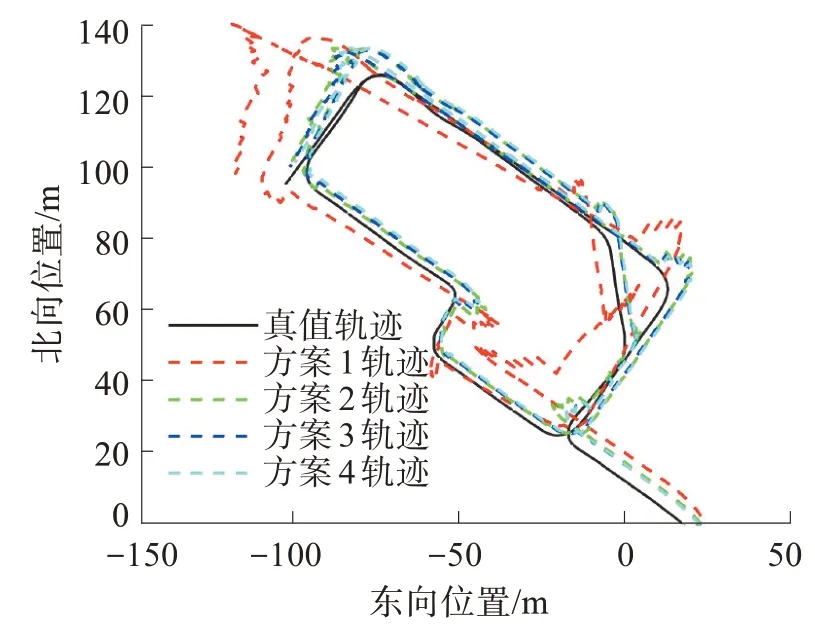
图7 实验1中断GNSS后推算轨迹对比Fig.7 Comparision of trajectories when GNSS is inter‐rupted in test 1

3.2 实验2（长直线）

表4 给出了实验2 采集的10 组数据在中断GNSS 信号800 m（大约280 s）后终点位置的平面误差的所有结果，表格的最后2 行分别给出了终点平面位置误差以及终点平面位置相对测量误差的RMS统计值。

表4 实验2中断GNSS信号800 m终点平面位置误差结果Table 4 Error of terminal position in the case of a 800 m GNSS signal outage (test 2)

统计结果显示，在长直线场景中，补偿以及在线估计MU 安装角和NHC 杆臂对定位精度无明显提升，方案1～3 的定位结果差异较小。这主要是因为在直线行驶时由IMU 安装角和NHC 杆臂产生的定位误差占比较小。此外，磁航向修正在实验2 中起到了一定的修正作用。相比于方案3，加入磁航向修正的方案4 终点平面位置误差RMS 值由96.2 m减小到87.9 m，精度提升了8.7%，终点平面位置相对测量误差减小到10.9%。

图8 给出了实验2 的一组典型数据在中断GNSS信号后，4种定位方案的推算轨迹对比图。从图8 中不难看出，沿着前进方向的位置误差是平面位置误差的主要来源。磁航向修正（方案4）虽然明显降低了航向漂移进而减小了左右方向的位置误差，但是它无法减小前向位置误差，因此磁航向修正带来的位置精度提升是有限的。另外，磁航向修正的直线轨迹存在弯弯曲曲的现象，这主要是因为磁干扰以及磁航向的噪声较大所导致。

图8 实验2中断GNSS后推算轨迹对比Fig.8 Comparision of trajectories when GNSS is inter‐rupted in test 2

此外，对比实验1 和实验2 的统计结果可以发现：

1)实验2 的终点位置误差漂移率要明显大于实验1。这一方面是因为惯导的精度是随时间发散的，实验1中断时长大约为140 s，而实验2中断时长达到了280 s；另一方面从水平位置误差曲线（见图9与图10）中可以看到，实验1水平方向的误差没有沿一个方向持续累积，而实验2 在直线段总体上呈发散趋势。这是因为实验1 在每次转弯后，NHC 的速度修正作用都会有效减小各个方向的速度误差；然而实验2 在长直线中NHC 的速度修正只能作用于固定方向的速度误差，对沿着轨迹方向的速度误差无效。另外，实验1在轨迹上还存在掉头，而惯导位置误差的一些影响因素（例如航向误差与前向速度误差）是与之相关的，进而导致水平方向的位置误差发生了逆转抵消的效应，而实验2由于是直线，自然没有“逆转抵消误差”的效果。因此，实验2 的终点位置误差漂移率要明显大于实验1。

图9 实验1水平位置误差曲线Fig.9 Error curve of horizontal position in test 1

图10 实验2水平位置误差曲线Fig.10 Error curve of horizontal position in test 2

2)相比实验1，磁航向修正在实验2 中带来的精度改善更加明显。这主要是因为实验2的误差发散时间较长以及没有轨迹掉头带来的“逆转误差”的效果，从而产生了较大的航向漂移，基于磁力计的相对航向约束得以发挥作用。而实验1本身航向误差较小，含有较高噪声的磁航向难以发挥显著作用。

3)相比实验2，IMU 安装角和NHC 杆臂补偿在实验1中带来的性能提升更加显著。由IMU速度投影到NHC适用点处在载体坐标系下的公式为：

故而杆臂补偿基本不会对直线段的NHC 产生影响。对于安装角而言，由于在直线段中航向角不可观，与水平位置相关的航向安装角易被航向误差吸收，从而难以表现其补偿作用。因此，在实验2长直线场景中，是否补偿安装角和杆臂对于定位性能影响不大。

4 结论

1）实验1（多转弯）结果表明，补偿IMU 安装角和NHC 杆臂可以充分发挥NHC 性能，有效提升定位精度（提升48%）；在线估计IMU安装角和NHC杆臂可以缓解实际车载场景中因为手机晃动带来安装角不固定的问题，进一步提升定位精度，该方案也在实验1 中取得了最好的精度，中断GNSS 信号500 m终点位置误差RMS 值为8.3 m，终点平面位置相对测量误差为1.66%。

2）实验2（长直线）结果表明，补偿和在线估计安装角和杆臂对定位精度影响不大；磁航向修正（方案4）可以抑制航向漂移进而提升定位精度，该方案在实验2 中取得最好的效果，中断GNSS 信号800 m后终点位置误差RMS 值为84.4 m，终点平面位置相对测量误差为10.56%，相比不使用磁航向修正的方案精度提升了8.7%。

本文所讨论的基于手机的车辆位置推算方法，还有待进一步完善，尤其在没有GNSS 信号的长直线场景下。例如，本文算法即使没有剔除干扰，磁航向修正在长直线的场景下都表现出了明显的积极作用，预期后续通过剔除磁干扰获得更准确的磁航向信息可以进一步提升定位精度。此外，还可以设法获取前向速度（例如车轮里程计或CAN总线车速信息）与NHC 构成三维速度约束，进一步提升GNSS拒止环境下的车载定位性能。