信号处理综合实验教学设计与实践

王绪虎， 侯玉君， 金 序， 宋传旺， 王辛杰， 陈建军

（青岛理工大学信息与控制工程学院，山东 青岛 266520）

0 引言

2016年，我国成为《华盛顿协议》的正式会员，该协议是工程教育本科专业认证的国际互认协议之一。2018年，教育部推出“保合格，上水平，追卓越”的三级认证体系来振兴本科教育。国内高校逐步重视工程教育专业认证工作，将其作为专业建设“追卓越”的重要抓手。工程教育专业认证标准（2022）明确规定，毕业生解决复杂工程问题能力的培养状况是评估评价一个专业的一项重要内容［1］。学生处理复杂工程问题的能力必须通过系统的理论和实践教学来实现，并且体现在课程的教学内容和教学评价中。

信号处理实验是电子信息类专业的一门综合实践课程，是电子信息类专业学生学习专业核心课程之后开设的一门综合实验。传感器阵列信号处理的波达方向（Direction of Arrival，DOA）估计问题［2-4］，是满足专业认证标准规定的复杂工程问题。信号处理实验课程组以培养学生处理复杂工程问题能力为目标，针对阵列信号处理中的DOA估计问题，设计了探究式的综合实验，给出了综合实验的设计方案和教学实践分析。

为了能够帮助学生快速地理解基于传感器阵列的DOA估计问题，本文以DOA 估计技术发展为主线，对波束形成（Beamforming，BF）方法［5］、最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）波束形成方法［6］、多重信号分类（Multiple Signal Classification，MUSIC）方法［7］以及利用凸优化和奇异值分解（Singular Value Decomposition，SVD）的L1-SVD方法［8］进行了原理分析，并设计了计算机仿真实验，分析不同方法的工作性能。针对上述各种DOA估计方法，开展了湖上试验，采集了实际环境中的数据，设计了实际数据的处理分析实验。通过湖上试验数据的处理分析，训练学生的工程思维，培养学生创新思维和处理复杂工程问题的能力。该综合实验案例已在我校信息与控制工程学院电子信息类专业（电子信息工程、通信工程）中实施，取得了较好的效果。

1 实验基本原理

1.1 传感器阵列接收信号模型

传感器阵列模型如图1 所示。传感器阵列为均匀直线阵，阵元数量为M，阵元间距d为入射信号半波长。假定有K（K＜M）个波长为λ 的远场窄带信号入射到传感器阵列上，信号的入射角度为θk（k＝1，2，…，K）。

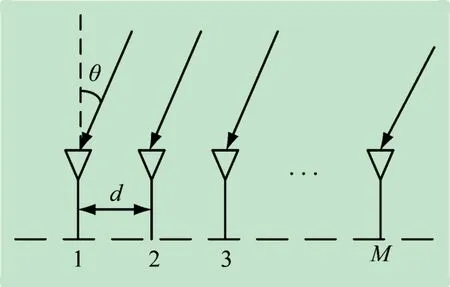
图1 传感器均匀直线阵模型

以传感器阵列左侧第1 个阵元为参考，第m个阵元接收到的信号可以表示为

式中：m＝1，2，…，M为阵元的标号；sk（t）是第k个入射信号；k＝1，2，…，K为入射信号的标号；nm（t）是第m个阵元接收的高斯白噪声；θk是第k个信号的入射角度。

阵列接收数据的矩阵形式可以表示为

式中，各个符号写成列向量的形式为：

A（θ）表示阵列方向矩阵；S（t）表示信号矩阵；N（t）表示噪声矩阵；A（θ）的列向量

1.2 波束形成

波束形成的基本思想是对阵列各阵元的接收信号进行加权求功率和［9］。令权向量w ＝［w1，w2，…，wM］T，则波束形成的输出为

式中：

表示阵列接收数据的协方差矩阵；

当权向量w ＝a（θ）时，即为传统的波束形成（Conventional Beamforming，CBF）。常规波束形成权值的模为1，可认为是按矩形窗设计权值幅度。权值w的模也可以按三角窗、升余弦窗、切比雪夫窗等形式设计，得到不同类型的波束形成器［9-10］。

1.3 MVDR方法

MVDR方法的基本思想是选取合适的权向量w在期望方向形成主波束，在非期望方向功率最小，最大程度减少基阵对非期望方向上激励的响应，实质上是构造了一个约束优化问题［11］。该优化问题可描述为

利用拉格朗日乘子法求解这一优化问题，可求得最佳权向量为

式中，R-1表示对阵列接收数据协方差矩阵求逆。阵列接收信号利用上述权值加权处理后，MVDR 波束形成器输出为

对式（12）进行谱峰搜索，PMVDR（θ）的K个峰值对应角度就是入射信号的波达方向。

1.4 MUSIC方法

MUSIC方法的基本思想是利用信号子空间和噪声子空间的正交性来估计信号的DOA。对阵列接收信号的协方差矩阵R进行特征值分解可得

式中：Σ 为R的M个特征值组成的对角矩阵；U 为R的特征值对应的特征向量构成的矩阵。

从矩阵U中选取M-K个小特征值对应的特征向量构成噪声子空间UN，利用UN可以求得空间谱函数

对式（14）进行谱峰搜索，PMUSIC（θ）的峰值对应角度即为入射信号的波达方向。

1.5 L1-SVD方法

L1-SVD方法的思想是将压缩感知理论与阵列信号相结合，构造过完备字典，然后利用数据矩阵的奇异值分解和L1 范数的凸优化，求解优化函数获得稀疏信号［12-13］。

将入射信号方位估计范围［-90°，90°］等间隔地划分为L个网格，假设每个网格方向θl（l＝1，2，…，L）都存在一个潜在的入射信号，则传感器阵列的流型矩阵具有L列，每一列都包含一个潜在的入射信号方位信息，因而构造出一个过完备字典

其中，L≫K。实际的入射信号在空域的分布是稀疏的，稀疏信号

式中：

单快拍时，通过求解下式表示的优化问题，可实现入射信号的方位估计，即求解出非零元素最少的解

优化问题的目标函数可以表示为

式中，λ表示非负平衡因子，通常很小，噪声强度不同，λ大小也不同。

快拍数为T时，目标函数可以表示为

快拍数T增大时，阵列接收数据矩阵的维数增大，直接求解式（19）的计算量会很大，从而导致估计结果出现偏差。为提升估计性能，减少运算量，L1-SVD方法首先对接收数据矩阵进行奇异值分解

式中：D ＝［IK0］T，IK表示K阶单位矩阵，0 表示K×（T-K）阶零矩阵。

因此，稀疏表示模型可以简化为

式中：SS（t）＝。

目标函数可重写为

转为二阶锥规划问题，可表示为：

最后，利用凸优化工具包CVX 中的函数对式（24）直接求解，即可得到信号（t）的稀疏谱，进而估计出目标的方位。

2 综合实验设计

2.1 实验设计思想

为培养学生处理复杂工程问题的能力，综合实验的设计既要具有基础性，又要具有一定的层次性，能够通过多阶的训练，提升学生的工程思维、创新思维和实践能力。为了达到基础性和层次性的要求，阵列信号处理综合实验的整体设计如图2 所示。

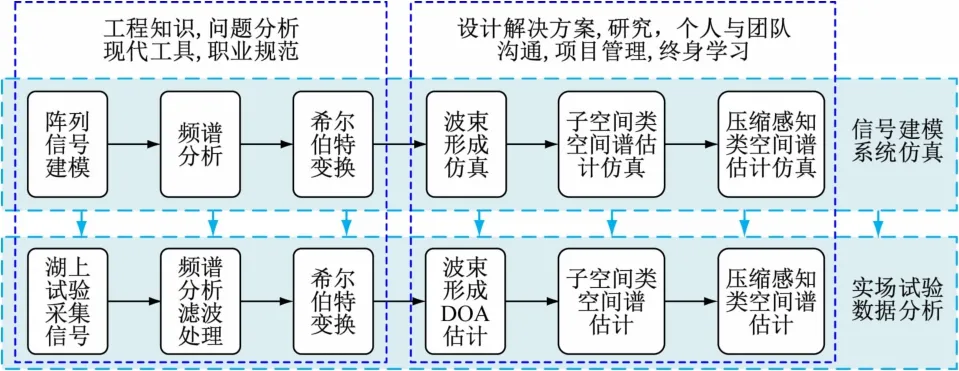
图2 综合实验设计图

（1）横向维度。实验内容从信号处理的基本知识点出发，涉及脉冲信号建模、频谱分析、滤波器设计与应用、希尔伯特变换等内容，通过这些初阶内容，让学生掌握工程知识，提升问题分析的能力，同时选择并熟练使用现代工具，了解专业的相关标准规范以及程序设计规范等。中阶内容为常规波束形成，以及类比窗函数引申出的三角加权波束形成、升余弦加权波束形成、切比雪夫加权波束形成等。高阶内容为最小方差无失真响应波束形成、多重信号分类方法和压缩感知类L1-SVD 方法。通过这些中高阶内容，培养学生设计复杂问题的解决方案，比较优化解决方案。在设计过程中，运用项目管理思想，通过充分的沟通研讨，最大限度地发挥个人和团队的效率，同时考虑非技术因素对技术方案的影响，认识到终身学习重要性，并具备自学的能力。

（2）纵向维度。针对实践任务，首先进行资料收集，通过分组开展理论分析与研讨，探索解决复杂问题的理论方案；其次依据理论方案，选择合适的现代工具进行信号建模、系统仿真，分析评价各种方法的特点；最后针对湖上试验数据进行处理分析，通过仿真实验结果与湖上试验数据处理结果的分析比对，以及复杂工程问题处理方案的优化探索，培养学生理论联系实际的意识，训练学生的工程思维，提升学生创新能力和工程实践能力。

2.2 仿真实验

以6 个阵元的均匀水听器直线阵为基础，探索不同的DOA 估计方法的工作性能。仿真实验中阵元间距d＝λ／2 ＝0.75 m，信号采样频率为36 kHz，快拍数N＝720，信噪比snr ＝10 dB，一个中心频率为1 kHz的远场窄带信号从某方向入射到水听器阵列。利用波束形成、MVDR、MUSIC和L1-SVD 方法等对入射信号进行估计。主要的实验任务包括：①阵列接收信号的建模；②信号的频域分析；③滤波器的设计及信号滤波；④信号希尔伯特变换；⑤波束形成方法估计入射信号DOA；⑥MVDR和MUSIC 方法估计入射信号DOA；⑦L1-SVD方法估计入射信号DOA。

图3 给出4 种波束形成方法估计的结果。图中：CBF为常规波束形成方法曲线；TriAng 为三角加权波束形成方法曲线；Cos 表示升余弦加权波束形成方法曲线；Cheb 为切比雪夫加权波束形成方法曲线。其中，CBF、Cheb、TriAng、Cos曲线的主瓣依次增大，且最高旁瓣高度依次降低，其中CBF、TriAng、Cos方法的多个旁瓣高度依次降低，而Cheb方法多个旁瓣具有相同的高度。引导学生类比于窗函数法设计FIR滤波器的基本原理理解不同加权方式的波束形成，帮助学生搭建信号时空处理的知识体系。

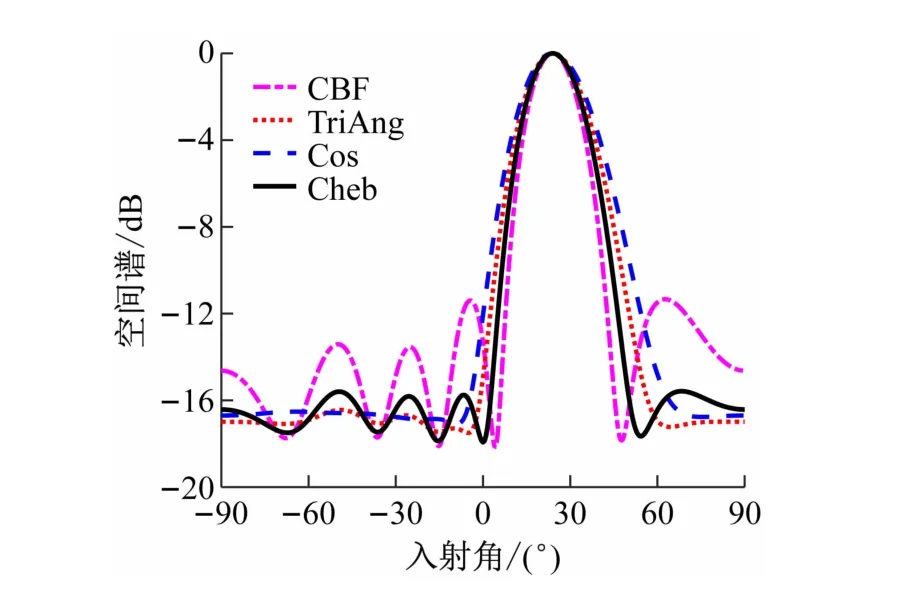
图3 4种波束形成方法空间谱

图4给出了CBF、MVDR、MUSIC和L1-SVD4 种方法的DOA估计结果。从图中可看出，CBF方法主瓣较宽，旁瓣水平最高，分辨能力最差；MVDR 方法的空间谱主瓣较窄，旁瓣高度低于CBF 方法的旁瓣；MUSIC方法的谱峰比MVDR方法的谱峰更为较尖锐，具有更好的分辨能力；L1-SVD方法的谱峰最尖锐，旁瓣最低，分辨能力最好。通过4 种方法的比较，帮助学生理解不同方法的方位分辨力以及抑制干扰的能力。

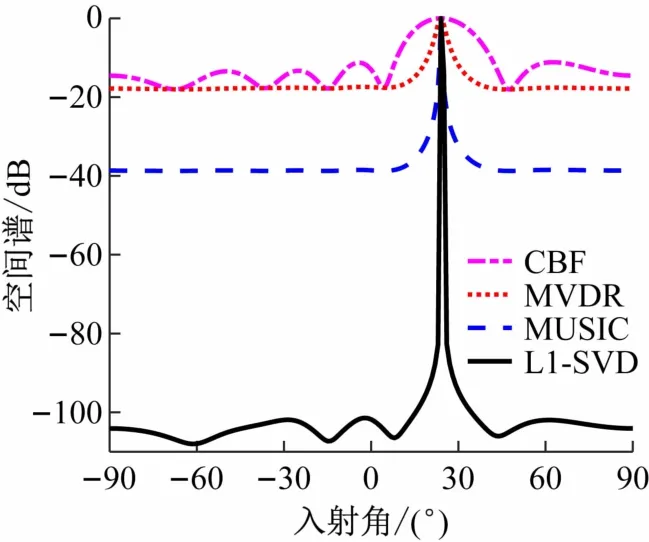
图4 4种方法的子空间方法空间谱

2.3 湖上试验数据处理分析

为验证上述方法在实际环境下的有效性和实用性，利用六阵元光纤水听器阵在丹江口水库进行了数据采集试验。6 个通道的采集数据波形如图5 所示。对各通道采集数据进行预处理，利用中心频率f0＝1 kHz，带宽400 Hz 的滤波器对接收信号滤波。图6给出了滤波前、滤波后的时域波形。图7 给出了滤波前、滤波后信号的频谱图。通过数据的读取存储、格式转换、信号滤波、频谱分析等环节，让学生升华对基础知识的认知。

图5 6通道采集数据波形图

图6 滤波前、后的时域波形

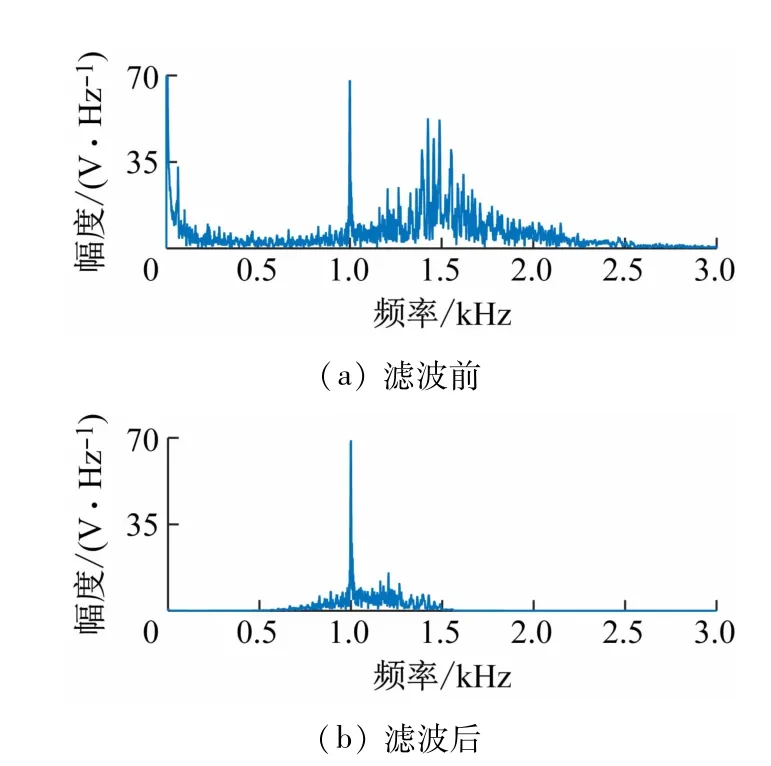
图7 信号频谱

分别利用CBF、MVDR 方法、MUSIC 方法和L1-SVD方法对光纤水听器阵的接收数据进行处理，估计入射信号的方位。水听器阵数据直接估计的结果如图8、9所示。图8 是4 种不同波束形成方法的估计结果，图9 是CBF，MVDR，MUSIC和L1-SVD方法的估计结果。从图8 可以可出，波束形成的4 种处理方法都可以成功估计出目标方位，主瓣较宽，旁瓣较高；从图9 可见，MVDR方法和MUSIC 方法也可以估计出目标方位，MVDR 方法具有较高的旁瓣，MUSIC 方法旁瓣较低，且基本无波动，L1-SVD 方法估计出两个目标。培养学生理解理论模型的局限性，以及不同处理方法在实际环境中的稳健性。

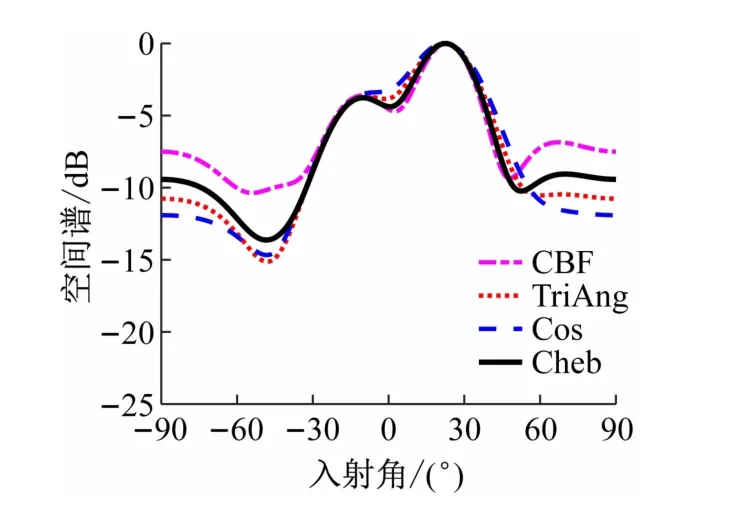
图8 数据滤波前波束形成方法空间谱

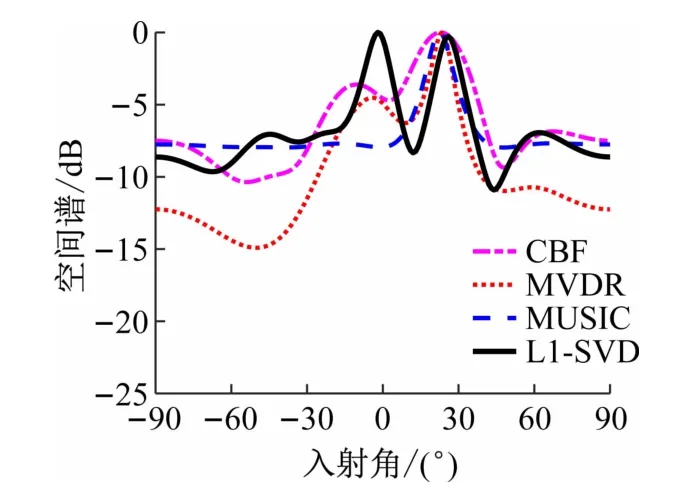
图9 数据滤波前子空间类方法空间谱

利用中心频率f0＝1 kHz，带宽400 Hz 的滤波器对光纤水听器阵各通道接收数据进行滤波，然后利用CBF、MVDR、MUSIC 和L1-SVD 方法估计入射信号的方位。图10 给出了4 种波束形成的估计结果；图11给出了CBF、MVDR、MUSIC 和L1-SVD 方法的估计结果。各种方法都成功地估计出1 个入射信号的方位，性能各有差异。通过滤波后不同方法结果的对比，以及滤波前后处理出不同结果的对比，帮助学生理解不同方法的性能及环境适应性。

图10 数据滤波后波束形成方法空间谱

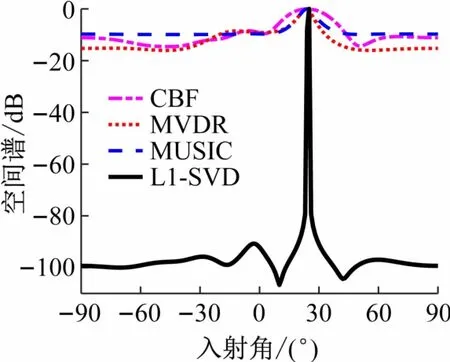
图11 数据滤波后子空间类方法空间谱

数据处理的过程，锻炼学生分析问题、设计复杂工程问题处理方案、使用现代工具以及程序规范等方面能力。对图8 ～11 数据处理结果的分析，培养学生个人与团队、沟通、问题分析能力，帮助学生理解理论与工程实际环境的差异性，训练学生的工程思维，培养学生创新思维和解决复杂工程问题的能力。

3 教学实施

（1）动员与任务发布。课程负责教师组织课程动员会，说明综合实验所需基本知识与现代工具，发布综合实验任务并讲解任务的具体要求。

（2）信息搜集与方案分析。搜集相关资料，分析DOA估计问题的解决方案，结合文献资料和代码，学习DOA估计的基本理论，比较选择不同技术方案。

（3）团队协作与系统仿真。学生分组组建团队，讨论理论及代码问题，探讨DOA 估计的不同方案，实现方位估计系统的设计，并对系统进行仿真分析。

（4）中期检查与实验数据发放。检查学生系统仿真情况，指导学生完善仿真方案和性能分析方法。介绍湖上试验系统配置，下发湖上试验采集数据，布置试验数据处理的具体要求。

（5）现场指导与方案优化。在实验室帮助学生解决试验数据处理过程中的难题，指导学生对试验数据处理结果进行分析，引导学生探索优化处理方法。

（6）实验方案及结果现场验收。每一小组在机房现场演示仿真和试验数据处理的程序及结果，老师根据指标对实验过程及结果进行打分。

（7）实验总结与报告撰写。对实验原理、实验过程、实验结果以及进一步优化方案进行总结，撰写实验报告，准备答辩。

（8）综合实验答辩。以小组进行集中答辩，主要阐述对综合实验原理的理解、复杂工程问题的处理方案以及处理方案的创新点和不足，小组成员逐一回答老师的问题。

4 教学评价

为了更合理地支撑电子信息类专业的毕业要求，更好地完成课程教学目标，信号处理实验课程组结合教学开展情况，针对该课程建立了多元化的学习效果评价体系，全面、客观地考察专业学生处理复杂工程问题的能力状况。信号处理实验的考核成绩构成如表1所示。

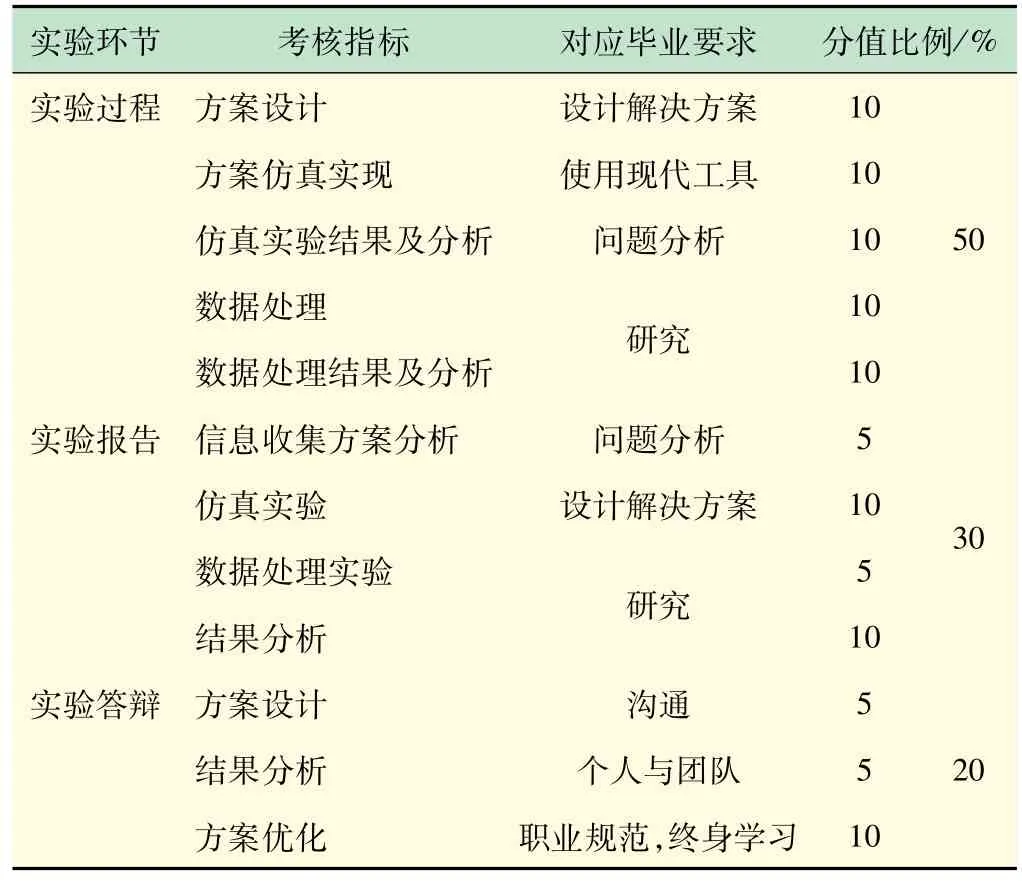
表1 信号处理实验学习效果评价表

信号处理实验课程根据支撑的毕业要求，制定了明确的课程目标。实验每个环节都有具体的教学目标和相应的考核标准，为客观公正地评价学生的学习效果提供了依据。该实验在青岛理工大学信息与控制工程学院通信工程、电子信息工程两个本科专业实施了2年，教学效果明显，学生时空联合信息处理的知识体系更为完善，解决复杂工程问题能力显著提升。

5 结语

新工科教育和工程教育专业认证对人才培养目标提出了新要求。信号处理实验是电子信息类专业的一门综合实践课程，课程组积极探索理论与实践相结合，以学生为中心，以产出为导向的教学模式。本文以水听器阵列的DOA估计问题为例，设计了信号处理综合实验的教学案例。实验内容既包含基础性内容，又具有高阶的训练内容，通过多层次的实验内容训练学生工程思维，培养学生创新思维，提高学生处理复杂工程问题的能力。水听器阵DOA 估计的多目标层次化实验方案已经在青岛理工大学电子信息类专业开展2年，取得了较好的效果，今后课程组将继续探索拓展信号处理实验课程的教学案例。