基于配电线路磁场逆问题的非接触电流检测反演方法

2023-12-30 03:17邱奕茗周强韦甜柳李巍巍马立修孙建超

南方电网技术 2023年11期

邱奕茗，周强，韦甜柳，李巍巍，马立修，孙建超

（1.山东理工大学电气与电子工程学院，山东淄博 255000；2.直流输电技术全国重点实验室（南方电网科学研究院），广州 510663）

0 引言

近年来，随着建立坚强智能电网、推进电网设施建设等一系列发展方针的相继提出，电网规模不断扩大，架空线路的数量和长度随之大幅增加，沿配电架空线路对其电量参数进行有效监测的需求日益增长。电流作为基本的被测物理量，其幅值、相位信息可以表征架空线路的运行状态和故障评估，为了确保电力系统的安全、可靠和经济运行［1-2］，需对架空线路的电流参数进行快速、准确的监测［3］。

目前，关于架空线路的电流参数测量方法主要分为接触式和非接触式两类。接触式测量因为设备与线路之间存在电气连接，所以测量结果相对精确，可靠性较高。但随着线路电压等级的提升，设备的绝缘强度也要随之提升，导致设备体积变大，缺乏灵活性，不易安装使用，制造成本大幅增加。非接触式测量可以在架空线路的安全距离外进行，降低了检测设备的绝缘要求和成本，保障测量的安全性。目前非接触电流测量大多采用传感器结合各种算法实现对线路电流的检测。由于配电线路下方产生的磁感应强度值随着距离的增加而衰减，现有检测方式及算法存在计算时间长、计算准确度低等问题，难以满足实际工程应用对测量精度的需求。针对以上问题，寻求一种安全、有效、精确的非接触式架空线路电流信号检测方法变得十分必要。

智能算法因高效、易实现等特点，在解决复杂的工程问题方面发挥了重要作用，因此许多专家学者在进行架空线路检测与诊断过程中融入了各种智能算法。文献［4］利用配电网发生故障时检测到的零序电流信号，结合改进二进制海洋捕食者算法对故障区域进行定位，该算法虽然兼顾了计算速度与精度，但在求解过程中容易忽略全局信息，陷入局部最优中。文献［5］利用果蝇优化算法计算满足要求的电力弹簧的最优参考电压，通过控制器实现对负载电压和线路电流的同步补偿，该算法的计算量小，复杂度低，但无法解决最优值为负数的问题，应用范围受限。文献［6］利用随机矩阵理论算法对配电线路电流信号进行采集分析，该算法不受线路运行状态影响，有良好的抗噪能力，但构建检测矩阵需要计算大量数据，难以满足快速计算的需求。文献［7-8］均采用磁阻互感器对架空线路电流所产生磁场进行测量，从而分析判断线路当前的运行状态，属于电磁场正问题即根据已知源的分布情况求解电磁场规律，为本文建立由场求源的逆问题电流反演模型提供了思路。文献［9］利用最小二乘近似法对搭建的缩小版三相架空线路模型进行线路电流反演，由于模拟环境为真空，未考虑环境干扰问题，反演误差过大，效果不理想。

针对上述问题，本文提出了一种基于磁场反演的非接触式三相交流架空配电线路电流测量方法。首先，结合磁场逆问题对线路磁场进行分析；其次，建立线路电流反演寻优模型，引入非支配排序遗传算法（non-dominated sorting genetic algorithm，NSGA-Ⅲ）和优劣解距离法（technique for order preference by similarity to ideal solution，TOPSIS）解决电流反演和解集筛选的问题，通过算例对比分析验证了本文所提出方法的有效性和准确性；最后，在所搭建的模拟三相线路电流反演试验平台上对本文所提出方法的实用性和准确性进行了验证。

1 架空配电线路工频磁场数学模型

1.1 工频磁场三维模型

时变电磁场中若各处的位移电流密度远小于传导电流密度，可忽略位移电流效应，按静态场处理。因此，配电线路产生的工频磁场可以认定为准静态场，即磁场仅由线路电流产生。此外，架空线路与地面距离较远，由复镜像原理产生的镜像导线对空间磁场影响微弱［10］，在计算磁场过程中只需要考虑实际架空线路的作用。图1 为载流长直导线计算模型图。

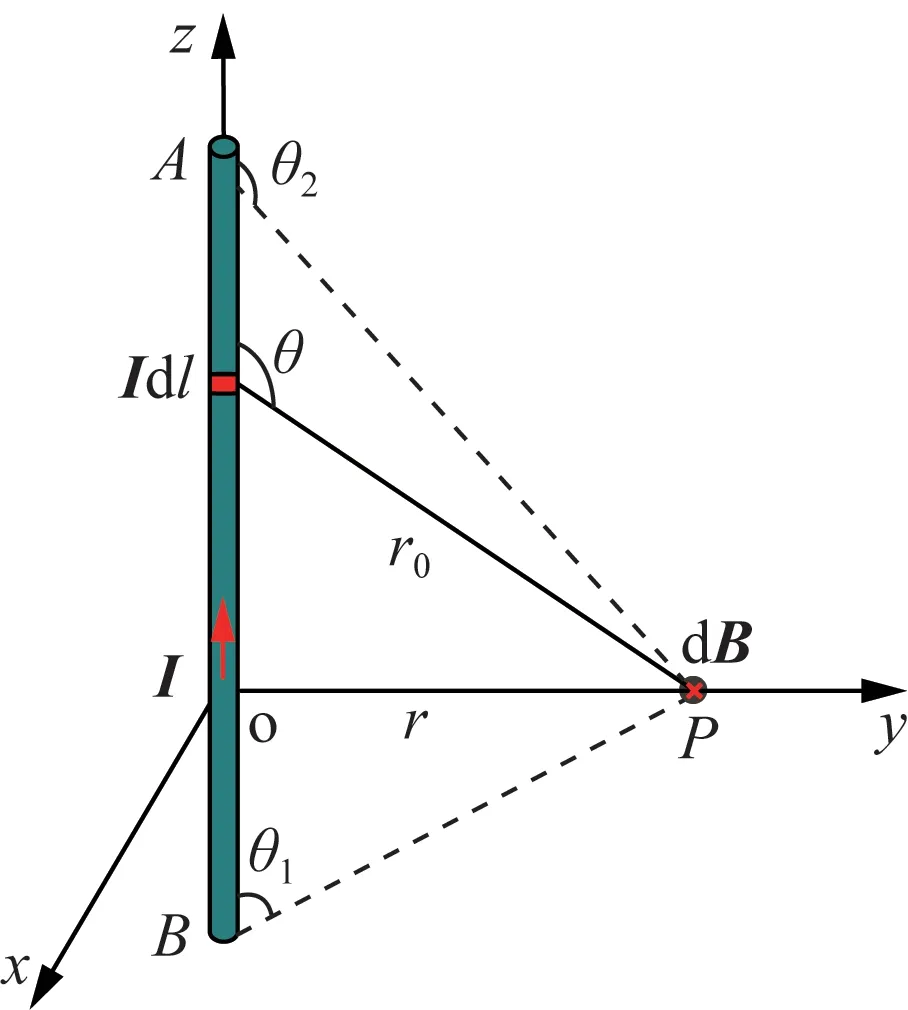
图1 载流长直导线磁场计算模型图Fig.1 Model of current-carrying long straight conductor for magnetic field calculation

根据毕奥-萨伐尔定律得到测量点P（x，y，z）处的磁感应强度计算公式如下。

式中：A、B为长直导线两端点；I为导线中的电流；Idl为选取的电流元；dB为电流元在测量点P处的磁场，方向与x轴反向平行；μ0为真空磁导率；r为导线到测量点P的距离；r0为选取的电流元到测量点P的距离；θ、θ1、θ2分别为测量点与导线和电流元之间的角度。

配电系统架空线路的档距相对较小，以架空线路弧垂最低点与地面之间的距离作为线路的高度，此时线路产生的磁场与无限长导线产生的磁场差异很小，由此可将架空线路近似为无限长导线。此时，式（1）中θ1→0，θ2→π，无限长导线在测量点P（x，y，z）处的磁感应强度计算公式如式（3）所示。

1.2 三维模型简化计算

考虑到实际工程应用和计算复杂度，将三维磁场模型转换成垂直于架空线路的二维磁场模型，架空输电线下方的磁场由三相电流共同产生，测量处的磁感应强度是由A、B、C 三相单独存在时产生磁场的矢量和［11-12］，如图2 所示。图中P1、P2、P3为水平排列在线路下方的测量点，rA、rB、rC为A、B、C 三相线路到测量点P2处的距离，BA、BB、BC为三相电流在测量点P2处的磁场方向。

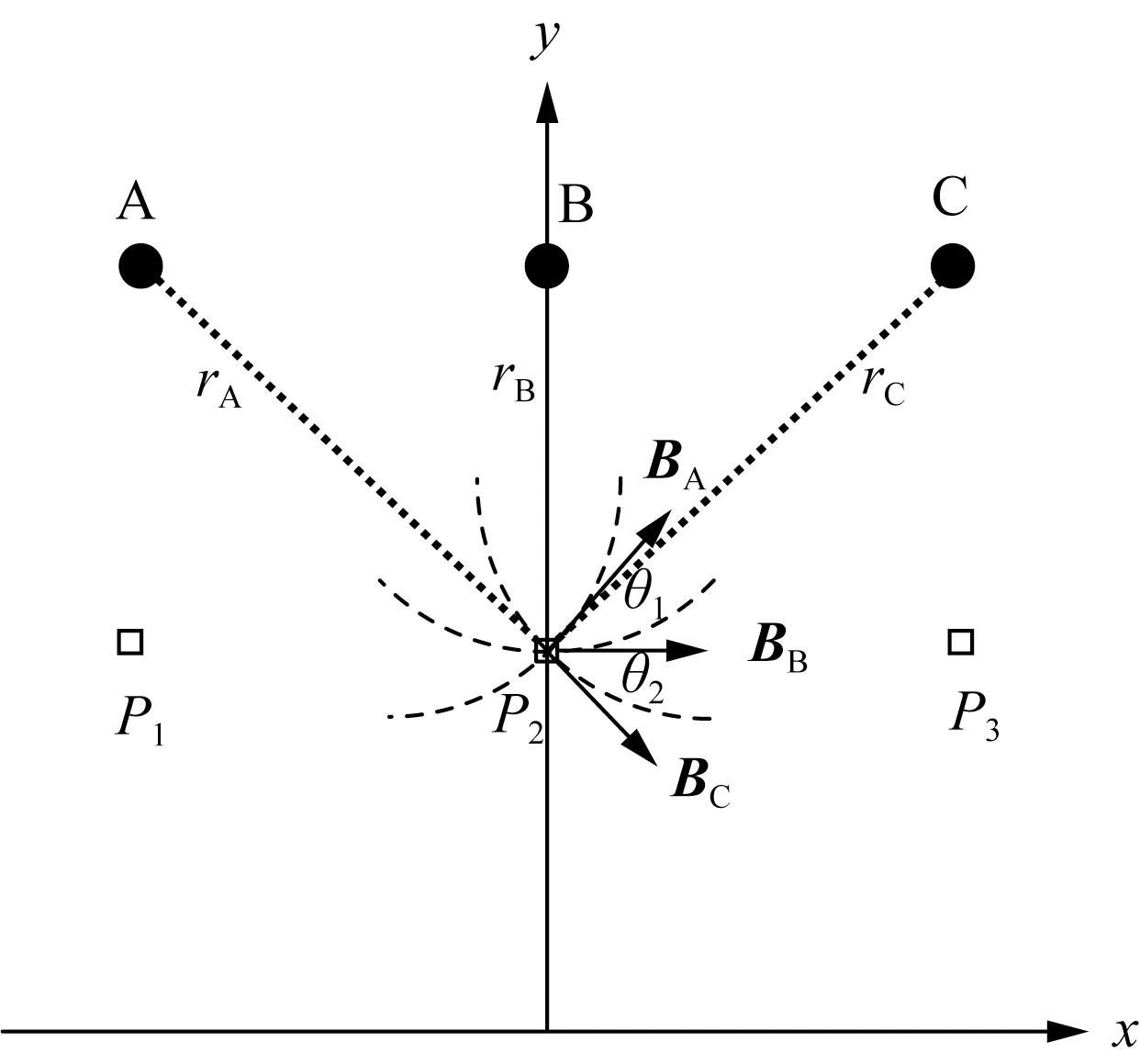
图2 三相架空配电线路磁场简化计算模型图Fig.2 Simplified calculation model of three-phase overhead distribution lines for magnetic field calculation

需要注意的是，当测量点处于线路正下方时，其磁感应强度y轴分量By=0［13］。根据磁场叠加原理得到测量点P处的磁感应强度为：

其中：

式中：IA、IB、IC分别表示为A、B、C 三相线路电流；θ1、θ2分别为BA、BB与x轴的夹角；ix、iy分别为x轴、y轴上的单位矢量；Bpx、Bpy、Bp分别为测量点P处的磁感应强度x轴分量、y轴分量和合成量。

1.3 寻优模型

测量点处的磁场是由三相电流分别所产生，三个矢量除了大小与方向不同外，它们之间的相角还存在一定的角度差。经过矢量合成后变成一个旋转矢量，在高度确定的情况下，旋转矢量的轨迹为椭圆形，如图3所示。

图3 磁场旋转轨迹示意图Fig.3 Schematic diagram of magnetic field rotation trajectory

椭圆的长轴用来表示该点磁感应强度合成量的最大值，随着位置的不同，磁场矢量的椭圆轨迹相应发生变化，椭圆长轴即磁感应强度最大值也随之变化。因此矢量合成后的测量点处的磁场最大值、x轴磁场分量和y轴磁场分量共同构成了测量点处磁场的全信息量即能够全面的反映该处的磁场分布信息。综上所述，为了提高线路电流反演结果的精确度，利用线下3 个测量点处工频磁场分量和合成量的理论值和实际值构造的寻优模型如式（6）所示。

式中：F1、F2、F3分别为工频磁场合成量、x轴分量、y轴分量所建立的目标函数；Bi、Bix、Biy分别为测量点i处磁感应强度合成值、x轴分量和y轴分量的理论计算值，以IA、IB、IC作为输入量计算；分别为对应的实际测量值。

式（6）中目标函数F1、F2、F3变量的约束条件为：

式中Imax、Imin分别为A、B、C 三相线路电流的上限值、下限值。

2 基于NSGA-Ⅲ算法的寻优与解集筛选

本文构建的配电线路电流寻优模型，包含3 个相互制约的目标函数F1、F2、F3，需要同时对3 个目标函数寻优得到三相电流IA、IB、IC，因此属于高维多目标优化的参数识别问题，所选用的优化算法需满足电流反演快速性和准确性的要求。

2.1 NSGA-Ⅲ算法寻优流程

NSGA-Ⅲ算法作为第三代多目标优化遗传算法，对第二代算法（NSGA-Ⅱ）的个体选择机制进行了改进，在处理高维多目标优化问题时，个体搜索速度快，目标空间中解集分布均匀，能够满足本文所建立工程应用场景的需求。

NSGA-Ⅲ算法流程如图4所示。

图4 NSGA-Ⅲ算法流程图Fig.4 Flow chart of NSGA-Ⅲalgorithm

1）种群初始化：随机生成父代种群（个体数量为N），预置均匀分布的参考点。

2）种群更新：父代种群通过交叉、变异等操作生成子代种群（个体数量为N）。

3）生成新种群：父、子种群合并，通过参考点选择机制筛选出N个优秀新个体组成新一代种群。

图5 种群选择示意图Fig.5 Schematic diagram of population selection

2.2 帕累托解集筛选

利用NSGA-Ⅲ算法对1.3 节中构建的电流寻优模型求解，得到的结果是包含众多解（反演电流值）的解集域而非单一值。由于解集数量庞大，人为筛选导致效率低下且在筛选过程中容易包含不确定的主观因素，得到的解准确率较低，如何从解集域中快速且准确的筛选出一组最优解，成为多目标优化过程中难以解决的问题之一［14］。

鉴于此，本文采用TOPSIS 法，根据有限个帕累托解与理想目标的接近程度来对解集进行选优。TOPSIS法的筛选流程如图6所示。

图6 优劣解距离法流程图Fig.6 Flow chart of TOPSIS

首先得到帕累托解集作为原始数据矩阵，对矩阵中的每组解进行指标类型（极大型、极小型、中间型）的统一即正向化处理，得到正向化矩阵。其次，寻找正最优解与负最优解，其中正最优解为每组解中不同元素的最理想取值，负最优解则相反。最后，根据式（8）计算每组解和正、负最优解之间的欧式距离进行可视化排序，排名越往前说明该解越理想。

3 算例分析与对比

本文以配电网系统35 kV 单回路三相架空线路为例，分别对架空线路在三相平衡和三相不平衡两种运行状态下的线路电流进行反演分析。在算例分析中，使用磁场传感器同步对3 个测量点在两个周期内采样40 组不同时刻磁感应强度值，通过添加噪声形成不同误差水平的模拟测量值，带入优化算法中依次对各时刻点进行反演。反演得到的数据值以曲线拟合的方式形成电流波形从而提取电流的幅值、相位参数信息。

3.1 “0”时刻反演结果与分析

单回路架空线路的A、B、C 三相采用水平排列方式，线路两侧悬挂点离地高度为15 m，相间距离l为1.6 m。考虑到35 kV 配电线路相比于高压及特高压输电线路的电压等级较小，线路下方的磁场衰减快、分布范围缩小［15-17］，因此将测量点1、2、3 水平排列在线路正下方且与线路之间的距离h为13 m。架空线路结构如图7所示。

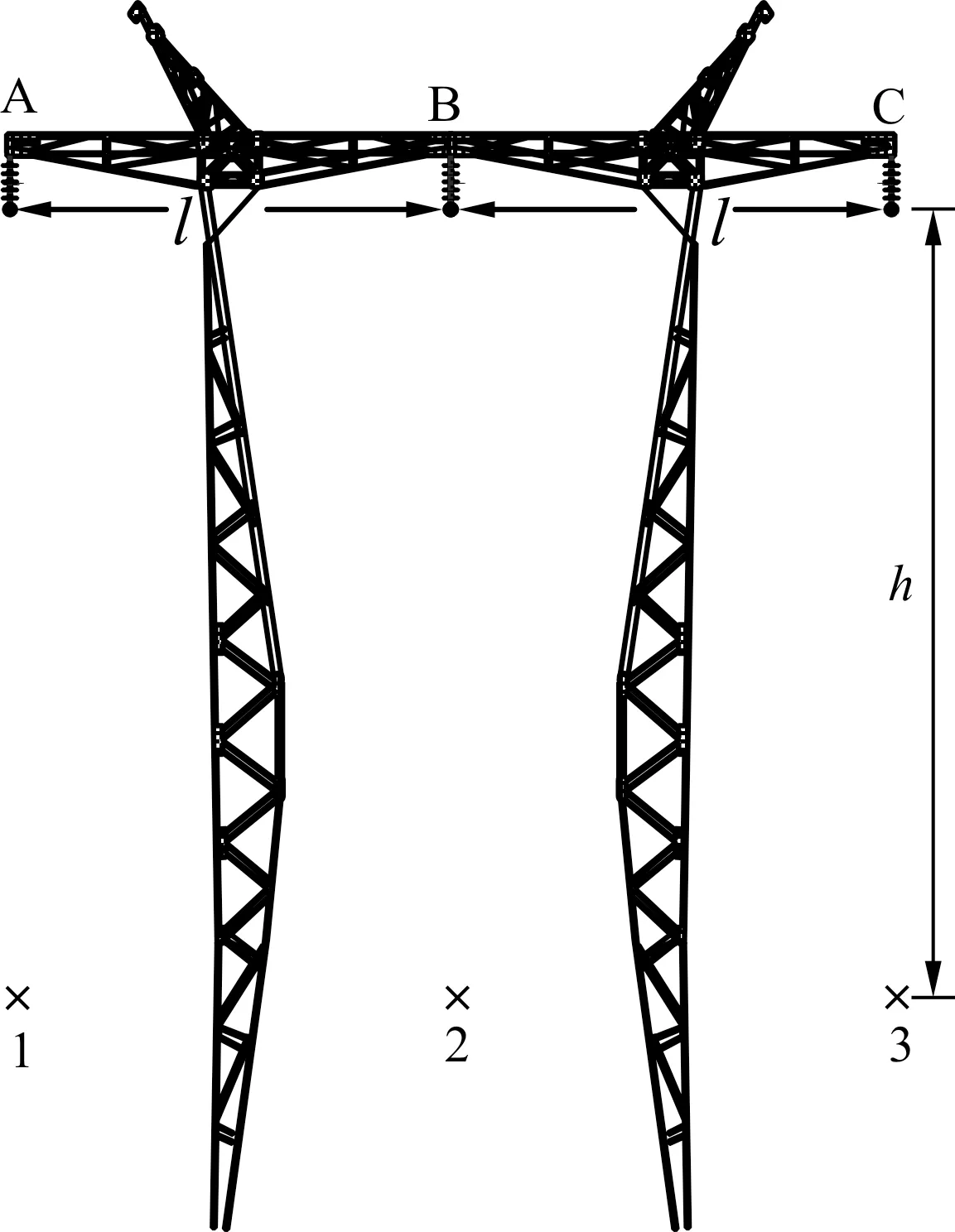
图7 三相架空线路和测量点结构示意图Fig.7 Structure schematic diagram of three-phase overhead lines and measurement points

在“0”时刻下，通过理论计算得到测量点1、2、3处的磁感应强度值如表1所示。

表1 磁感应强度理论计算值Tab.1 Theoretical calculation values of magnetic induction density

考虑到实际测量时并非处在无任何干扰的理想环境中，存在采集到的数据中会夹杂噪声且测量点位置可能存在偏移等问题，因此对表1 中的数据添加±6%的误差来模拟实际测量数据，如表2所示。

表2 磁感应强度模拟计算值Tab.2 Simulated calculation values of magnetic induction density

将表2 中的模拟计算值代入NSGA-Ⅲ算法中反演求解电流值，得到包含190 组可行解的帕累托解集，结合TOPSIS 法对解集进行可视化排序筛选出最优解，结果如图8所示。

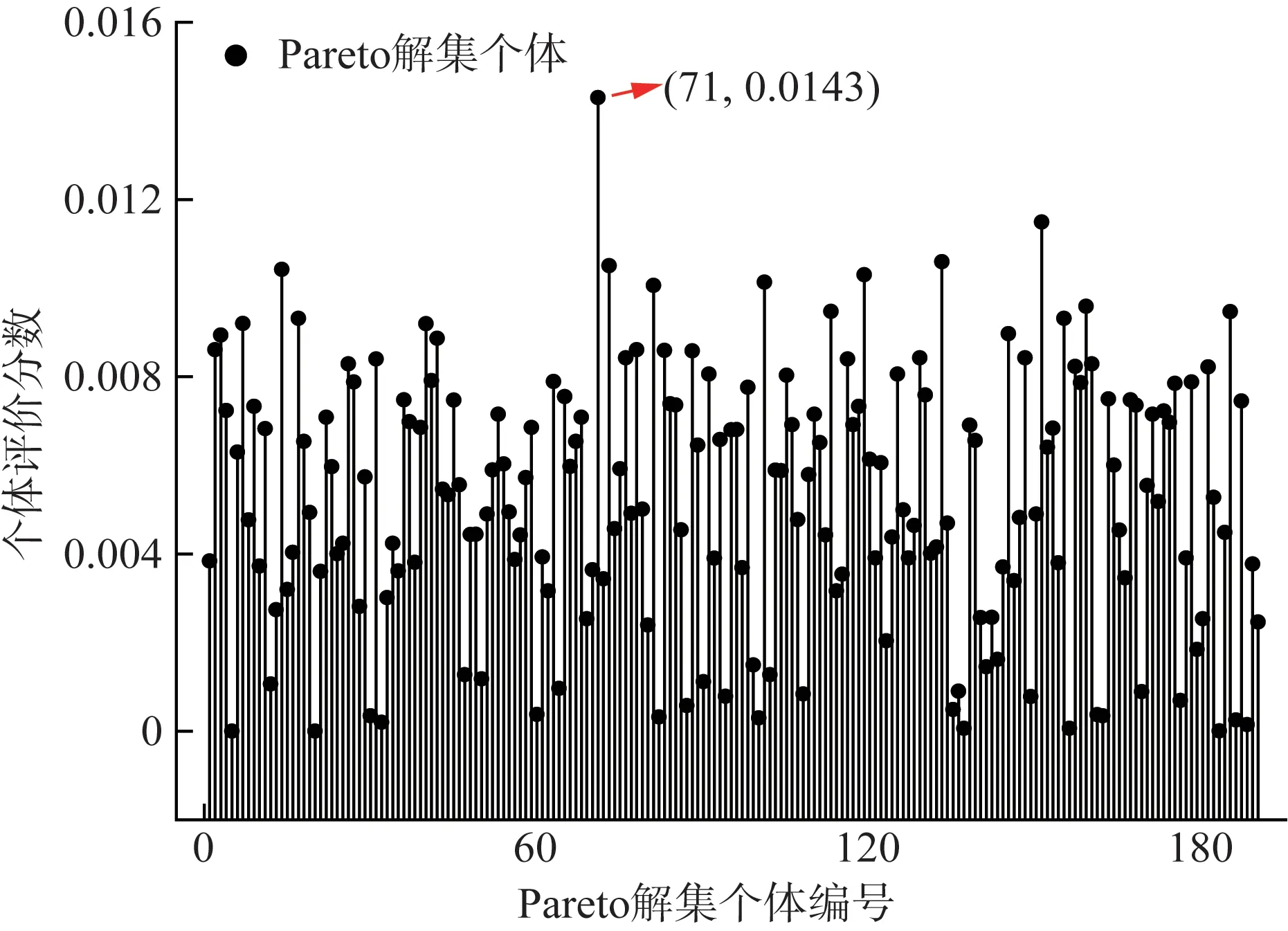
图8 解集筛选排序图Fig.8 Sorting diagram of solution set screening

图8中每一组解都代表反演得到的A、B、C 三相电流的数值，都由一个坐标点（x，y）来表示，x轴对应每一组解的编号，y轴对应每一组解的评价分数。其中第71 组解的评价分数在所有解的排序中最高，因此成为“0”时刻电流反演的最优解，如表3所示。

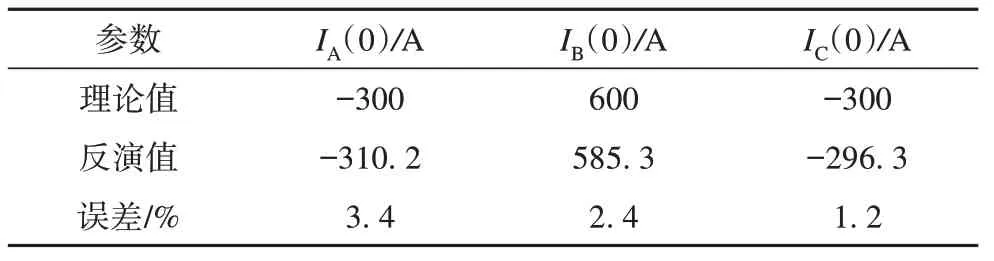
表3 三相电流反演值Tab.3 Inversion value of three-phase currents

由表3 可以看出，筛选出的最优解与理论值较为接近，误差最大为3.4%，说明本文所提方法能够对电流参数进行有效识别，满足实际应用需求。

3.2 三相平衡状态反演结果与分析

当线路正常运行时，三相对称电流瞬时表达式为：

其幅值向量表达式分别为600∠-120 °、600∠0 °、600∠120 °。

本文第3.1 节中已表明NSGA-Ⅲ算法对于“0”时刻的线路电流反演具有较好的效果，将三相平衡状态下同步测量的不同误差水平的磁感应强度值代入优化算法中反演并对经过TOPSIS 法筛选出的三相电流各时刻电流值最优解进行曲线拟合，结果如图9所示。

由图9 可以看出，反演得到的三相电流值经过曲线拟合后得到的电流波形基本呈正弦规律变化，对图中电流波形的幅值、相位参数进行提取，列于表4。

表4 不同误差的三相电流反演结果（三相平衡）Tab.4 Inversion results of three-phase currents with different error levers（three-phase balance）

通过表4 可以看出，磁感应强度测量数值的精准度与三相电流参数的反演结果呈正相关，三相电流参数的反演数值随着磁感应强度测量误差的增大而增大。在不同测量误差水平下，反演电流参数值基本在所设定理论值的3%范围内上下浮动。当测量误差水平达到10%时，与理论值相比幅值最大偏差为38.8 A，相位的最大偏差为3.9 °，整体反演精度较高。

3.3 三相不平衡状态反演结果与分析

三相不平衡是整个电力系统中的常见问题，它的存在会使线路损耗增加［18］，造成能源的浪费，还会导致高低压设备损坏，影响电力系统的安全可靠运行，因此对该状态下的线路电流进行监测也是十分必要的。设线路处于三相不平衡状态时，三相电流的瞬时表达式为：

其幅值向量表达式分别为900∠-150 °、600∠0 °、400∠100 °。

A、B、C三相电流在磁感应强度测量误差水平分别为±3%、±6%、±10%情况下的反演值和拟合曲线如图10所示。

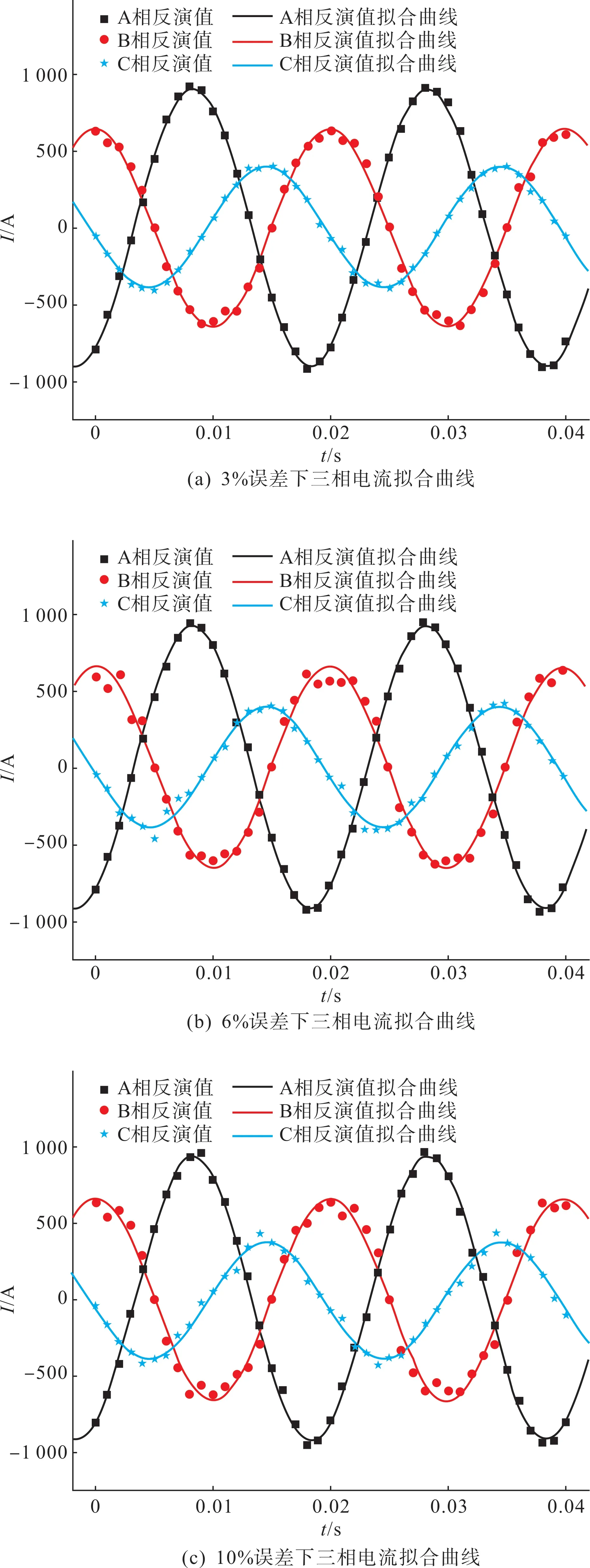
图10 三相电流反演结果（三相不平衡）Fig.10 Inversion results of three-phase currents（three-phase unbalance）

对图10 中拟合得到的电流波形进一步提取电流的幅值与相位参数并列于表5。

表5 不同误差的三相电流反演结果（三相不平衡）Tab.5 Inversion results of three-phase currents with different error levers（three-phase unbalance）

当架空线路处在三相不平衡状态时，电流的幅值和相位均发生改变。从表5 中可以看出，A、B、C 三相线路反演电流的幅值和相位与三相平衡状态时相比较，偏差都有所增大，B 相电流幅值最大偏差为58.8 A，C相电流相位最大偏差为3.4 °，但仍与理论值较为接近。

综上所述，当磁感应强度的测量误差小于10%时，本文所提的反演方法可以较好地反演出所需的三相电流参数信息。

3.4 算例求解结果对比分析

为了验证本文所选用算法的性能优势，分别采用NSGA-Ⅱ与NSGA-Ⅲ算法对1.3节中构建的多目标优化模型进行求解。

NSGA-Ⅱ与NSGA-Ⅲ算法的流程框架大致相同，只是在个体选择机制上有所不同：NSGA-Ⅱ算法通过计算不同个体之间的拥挤距离来对同一非支配层中的个体进行筛选，在解决双目标优化问题时，搜索解的速度快，解集分布均匀［19］。当目标函数上升到3 个及以上时，由于非支配解数目骤加，算法搜索速度下降，继续使用拥挤距离筛选机制难以保证个体的多样性［20-24］，极易陷入局部最优解中。为了解决这些问题，NSGA-Ⅲ算法对个体选择机制作了改进，引入广泛分布的参考点用以保证个体的多样性和解分布的均匀性［25］，使其容易找到全局最优解，适用性更强。

三相平衡状态下测得的“0.004 s”、“0.008 s”、“0.012 s”、“0.016 s”4 个不同时刻磁感应强度，添加±3%的噪声，代入NSGA-Ⅲ算法中反演，经TOPSIS 法筛选出的各时刻最优解列于表6，所得帕累托解集在目标空间的分布情况如图11所示。

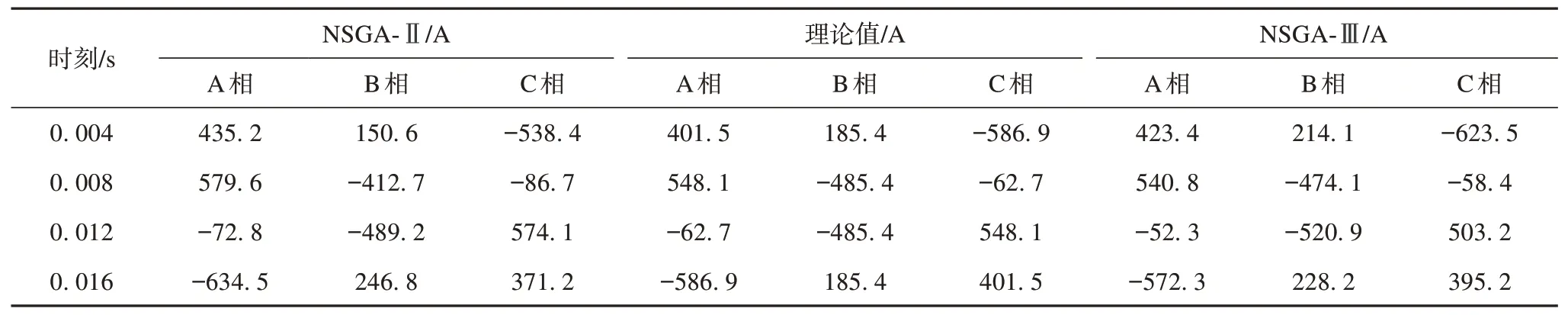
表6 不同时刻各算法的三相电流反演值（三相平衡）Tab.6 Inversion values of three-phase currents with each algorithm at different time（normal operating state）

从解的反演结果来看，表6 中在不同时刻下NSGA-Ⅲ算法的反演值与理论值相比，最大偏差为42.8 A，最小偏差为4.3 A。而NSGA-Ⅱ算法的最大偏差为72.7 A，最小偏差为3.8 A，在二者最小偏差几近相同时，最大偏差值相差一倍。

从解的分布情况来看，图11 中两种算法在不同时刻得到的帕累托解集，在目标空间中都有部分解相重合，说明二者的优化方向基本一致。相比于NSGA-Ⅱ算法在目标空间内有“聚堆”现象，NSGA-Ⅲ算法得出的帕累托解则在目标空间内分布均匀。

以上两种情况均表明，对于本文所构建的多目标优化模型，NSGA-Ⅲ算法的反演效果优于NSGA-Ⅱ算法。

表7 列出了两种算法在配电线路处在不同运行状态时的计算时间均值，在设定条件相同的情况下相比于NSGA-Ⅱ算法，NSGA-Ⅲ算法的计算速度更快，更容易满足实际工程应用的需要。

表7 算法计算时间均值Tab.7 Mean of calculation time of the algorithm s

综上所述，NSGA-Ⅲ算法在所有对比条件均获得最优指标，解集分布均匀，收敛性强，整体优化性能更好。

4 试验验证

4.1 试验平台搭建

为验证本文提出的电流检测方法在反演三相架空线路电流参数的准确性和优势，搭建如图12 所示的三相架空线路电流反演试验平台。

图12 电流反演试验平台Fig.12 The experimental platform of current inversion

图12 中模拟三相架空线路无故障运行状态下的电流反演，线路的相间距离为0.35 m，离地高度为1.5 m，测量探头布置在下方且探头处离地高度为0.1 m。三相电流发生器能够实现三相电流在0～1 000 A 范围的的无级调节，本试验通过调节电流发生器参数将模拟三相线路中的电流限制在20 A。试验过程中，模拟线路下方探头将测量得到的磁场数据通过连接线实时存储在高斯计中，设置高斯计在每个周期内（0.02 s）均匀的选取10 个时刻点并连续采集5个周期，采集到的磁场数据如图13所示。

4.2 试验结果及分析

通过图13 可以看出，模拟架空线路在探头处产生的磁场的已经相对微弱，随着电流的变化，测量得到的磁场分量及合成量做近似正弦变化。其中A、C 两相线路下方磁场的幅值变化趋势大致相似，但B 相所受影响较大，线路下方测量到的磁场在x轴上的分量在0 μT 附近上下波动，磁场合成量的值基本由y轴上的分量来提供。

将图13 中的磁场数据代入本文所提出的电流反演方法中进行求解，结合TOPSIS 法筛选出不同时刻下最优的反演电流值并拟合为反演电流曲线，如图14所示。

图14 三相电流反演结果Fig.14 Inversion results of three-phase currents

提取图14 中三相电流拟合曲线的参数信息，可得反演电流的相量表达式如表8所示。

表8 三相电流反演值Tab.8 Inversion values of three-phase currents

由表8 可以看出，与实验施加的电流值相比较，反演电流的最大幅值偏差率为6.2%，相位最大偏差为3.2 °。由于电流发生器、模拟架空线等设备与环境的影响，输出及线路中的流过的电流并非绝对的三相平衡，所以线路中的电流幅值相位信息本身带有较小的偏差，结合试验反演出的线路电流情况来看，本研究所提出的方法具有较好的准确性，具有一定的实际工程应用价值。

5 结论

针对配电系统中大量架空线路电流难以实现非接触式有效检测的问题，本文提出了一种基于磁场反演的非接触式三相架空线路电流检测方法，采用NSGA-Ⅲ算法和TOPSIS 法对构建的三相电流反演寻优模型进求解，得出结论如下。

1）通过对线路电流“0”时刻、三相平衡状态、三相不平衡状态下的线路电流反演结果分析可知，本文所提出的方法能够对电流参数进行有效识别，具有良好的有效性和准确性。

2）文中对帕累托解进行筛选所采用的优劣解距离法（TOPSIS），能够得到满足决策者偏好的最优解，筛选效果出色，适用于本文所构建的工程应用场景。

3）通过算例对NSGA-Ⅱ和NSGA-Ⅲ两种优化算法进行对比分析，能够看出在相同的条件下NSGA-Ⅲ算法的求解速度更快、解集分布更均匀、收敛性更好、反演结果更精确，满足实际工程应用实时性和准确性的需求。