面向多目标联合电力巡检的车载无人机协同巡检路径规划方法

梁华尘，周稳，倪旭东，胡康生，王倩倩，周智博

（1.国网安徽省电力有限公司滁州市城郊供电公司，安徽 滁州 239000；2.东南大学网络空间安全学院，南京 210000）

0 引言

近年来，在“碳达峰碳中和”新背景下，构建以电网为枢纽的新型电力系统成为实现“双碳”目标的重要途经［1］。输电网作为电网的重要组成部分，因其在自然恶劣环境下长期运行，外部侵蚀和内部损耗等一系列问题会对自身稳定运行带来不利影响，所以需要定期巡视和维护预防事故的发生［2-3］。

传统的输电线路巡检以人工巡检方式为主，其劳动强度大，工作条件艰苦，劳动效率低［4］，已不能适应新时期输电网发展和安全运行的需要。相较于人工巡检方式，无人机电力巡检具有操作灵活、巡检成本低、巡检效率高、显著降低劳动强度［5-6］等特点。随着技术的不断发展，采用无人机电力巡检逐渐成为输电线路巡检的重要手段。受限于无人机航迹规划难、续航时间短和远距离机动能力弱等问题［7］，现阶段无人机无法胜任实际巡检场景下较远距离的连续巡检任务。为了解决这一问题，巡检车搭载无人机协同巡检的新模式受到了有关研究者的关注，该模式实现了车与无人机优势互补，极大提高了无人机电力巡检的自动化程度和巡检效率［8］。无人机进行输电线路的电力巡检作业时，不同的巡检路径所耗费的时间和经济成本存在较大差异性。因此，无人机电力巡检路径规划问题成为无人机电力巡检作业的核心问题。

针对上述问题，已有学者对无人机电力巡检路径规划问题开展了相关研究工作。文献［9］针对电力杆塔三维巡检路径提出了一种改进快速随机搜索树（rapid-exploration random tree，RRT）算法，克服了在狭窄空间难以找到可行路径问题。文献［10］构建了面向电力杆塔巡检“无人机-旅行商”问题（travelling salesman problem with drone，TSP-D）模型，提出了奇偶分层编码方式的遗传算法求解该模型。文献［11］研究了“巡检车+无人机”协同巡检作业模式下无人机任务分配问题和巡检车路径规划问题。文献［12］提出了一种异地起降的单车多无人机协同电力巡检方式。但是以上文献均未涉及到电力线路巡检内容和无人机可悬停这一策略。文献［13］考虑了车载无人机协同巡检模式下对电力线路进行巡检路径规划问题，运用启发式算法和模拟退火算法求解。文献［14］考虑了无人机电力巡检轨迹遵循架空线跨度曲线，但未进行仿真验证。但以上文献均未考虑电力杆塔巡检过程和无人机可悬停这一策略。

综上所述，目前无人机电力巡检领域涉及路径规划的研究尚不完善，仍有以下问题有待进一步研究：1）未对以电力线路和电力杆塔为联合巡检目标的车载无人机协同巡检路径规划方法进行进一步研究。2）在车机协同巡检过程中，未考虑实际情况下无人机可悬停等待巡检车这一情况。3）未考虑无人机在不同阶段的飞行参数的差异性。

针对以上问题，本文基于电力杆塔和电力线路为多目标联合电力巡检任务，对车载无人机协同巡检路径规划问题开展了相关研究。本文首先在已有研究的基础上，根据“图论”相关理论建立了计及电力杆塔和电力线路联合电力巡检的车载无人机协同路径规划模型。其次在模型求解过程中首先根据本模型特点采用改进中国邮递员求解最佳输电线路巡检路线；并提出一种离散杆塔分割弧算法应用到巡检过程中，可求得较优的路径规划方案，并分析了不同场景下不同策略对解的影响；结合模型相关特点，利用模拟退火算法对该方案进一步优化，在该算法优化过程中，提出了符合本模型特点的领域搜索算子以完成模型求解。最后通过算例进一步验证的模型和算法的合理性和有效性。

1 车载无人机协同电力巡检路径规划模型

1.1 问题描述

面向多目标联合电力巡检的车载无人机协同巡检过程如图1 所示，该过程是指巡检车搭载无人机从运维站出发，沿着巡检车停靠点移动，在合适的停靠点停靠并放飞无人机。无人机由停靠点飞向输电线路，开始对电力杆塔和电力线路协同巡检，完成全部输电线路巡检任务后，巡检车搭载无人机返回运维站。

1.2 策略分析

无人机进行某段电力巡检过程如图2 所示。方块为车辆停靠点，圆圈为电力杆塔，巡检车行驶时间用T表示，无人机飞行时间用t表示，无人机的续航时间用θ表示。

图2 巡检单元示意图Fig.2 Sketch diagram of inspection unit

1）不考虑无人机悬停等待

式（1）表示巡检完b杆塔返回满足约束条件，在某些极端场景下TAB≥tAa+tab+tbB，则会造成无可行解的情况。式（2）表示无人机飞出点c满足续航要求，但由于无人机先于车辆到达停靠点导致该杆塔飞出点为不可行解。

2）考虑无人机悬停等待

式（3）和式（4）扩大了可行解的约束范围，使得无人机飞出点b、c均为可行解。

由上可知，考虑无人机悬停等待在不考虑无人机悬停等待的基础上扩大了解的空间，避免了极端条件下巡检过程中不可行解的出现，减少了无人机飞入飞出的次数，缩短了无人机的飞入飞出时间。

1.3 数学模型

计及杆塔和电力线路联合巡检的车载无人机协同巡检路径规划问题可以用图G(V，E)表示，V表示图中所有点的集合，其中包括运维站点λ0，巡检车停靠点集合Vp={p1，p2，…，pn}，其中pn表示第n个巡检车停靠点；以及无人机在输电线路飞入飞出点集合Vλ={λ1，λ2，…，λm}，其中λn代表第n个无人机飞入飞出点，用数学形式可表示为V={λ0}∪Vp∪Vλ。E表示为图中所有弧的集合，其中包括巡检车行驶路段集合Ec={i，j|i，j∈Vp∪{λ0}}，无人机输电线路飞行路段弧集合Eu={i，λk，λk+1，j|[i，j∈Vp∪λ0，k∈Rl]} 用数学形式可表示为E=Ec∪Eu。R表示巡检单元集合，其中包括负载巡检单元集合Rl={1，…，a，a+2，…，b，b+2，…，m-1}，空载巡检单元Rnl={0，a+1，b+1，…，m}，用数学形式可表示为R=Rl∪Rnl，其中a、b、m为巡检单元的巡检序号。

1.3.1 目标函数

本文以车载无人机协同电力巡检任务总用时最小作为优化目标，构建如下目标函数。

式中：Z为车载无人机协同电力巡检任务总用时；为第k个巡检单元巡检车行驶路线的决策变量；为第k个巡检单元无人机巡检作业的决策变量；dij为停靠点之间的距离；分别为巡检车停靠点与无人机飞入飞出点的距离；为第k个巡检单元无人机巡检输电线路总长度；vc为巡检车在停靠点间的平均行驶速度；vu1为无人机飞入飞出输电网的平均飞行速度；vu2为无人机巡检电力线路时的平均飞行速度；αk为第k个巡检单元巡检杆塔数量；Tg为无人机精细化巡检杆塔耗费时长。

1.3.2 约束条件

1）巡检车停靠点出入度约束

2）运维站出入度约束

3）巡检车停靠位置约束

4）无人机执行巡检任务约束

5）停靠点访问顺序递增约束

式中：gi∈N+（正整数集合），∀i∈Vp，gi为辅助决策变量，其中分别为第k个巡检单元的无人机的回收点序号以及起飞点序号。

6）无人机降落放飞点重合约束

7）无人机降落放飞点重合约束

8）负载巡检单元车辆行驶时间约束

2 车载无人机协同电力巡检路径规划模型求解

输电网巡检路线属于弧路由问题范畴，传统弧路由问题可通过中国邮递员问题（Chinese mailman problem，CPP）来求解，本文结合电力巡检相关特点，对CPP 作出相关改进，用于求解电力巡检的巡检路线。无人机飞入飞离电网点的选取属于连续优化问题，有无限多可行方案，为了把它作为离散优化问题去分析，通常是把平面上的每条边用多边形链来近似［15］。本文以电力杆塔所在位置作为离散优化的离散点，提出了离散杆塔分割弧算法。将离散杆塔分割弧算法与改进CPP 相结合，在遍历输电网中所有奇点后选取最优解作为初始巡检方案，并在求得的初始方案的基础上结合模拟退火算法进一步优化。求解策略如图3所示。

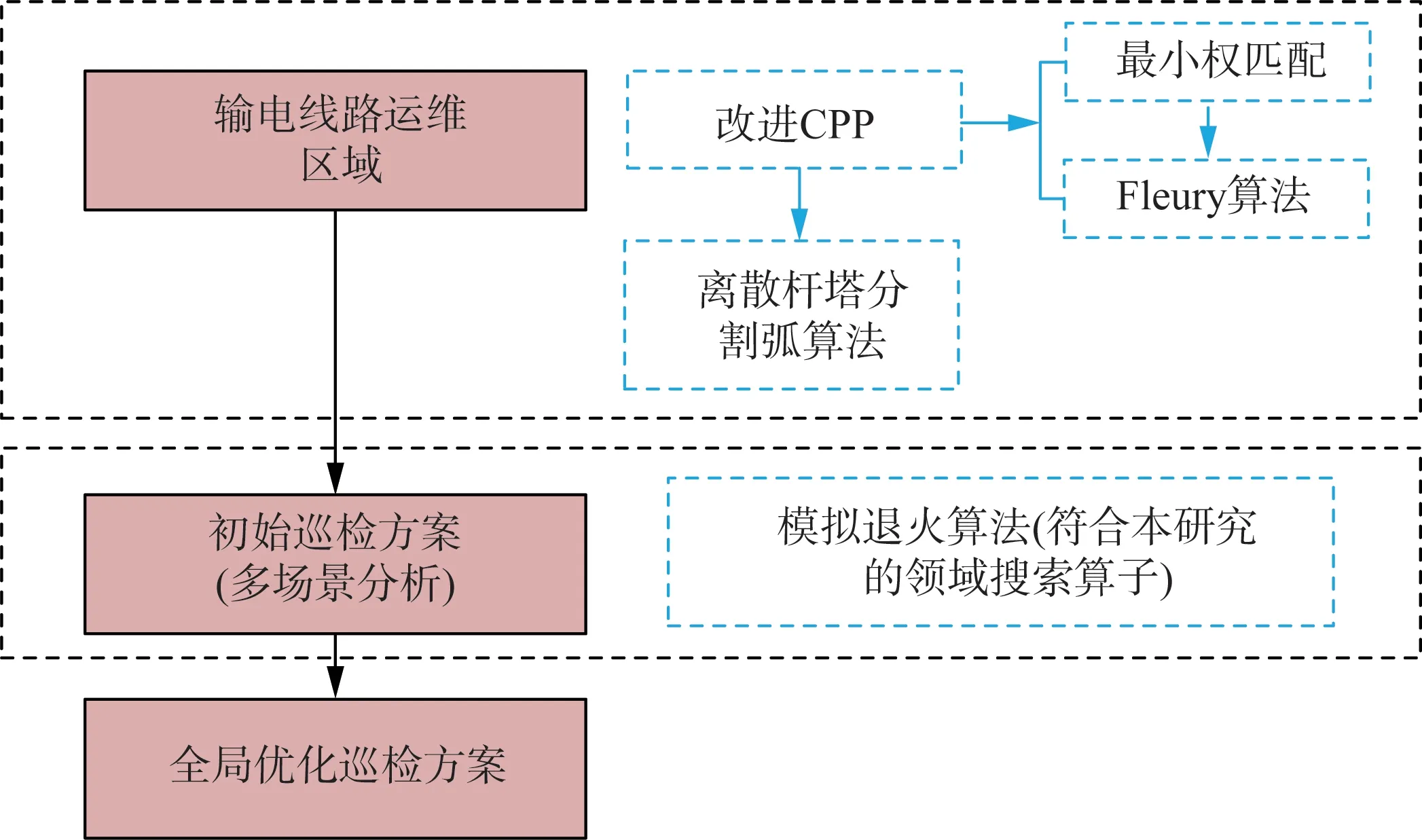
图3 模型求解策略图Fig.3 Diagram of model solving strategy

2.1 改进中国邮递员问题

中国邮递员问题是：一个邮递员每次上班，要走遍他负责送信的所有街道最后回到邮局，应怎么走才能使所走的路程最短［16］。

本文待巡检的输电线路网络可抽象为无向连通图G(V，E)，V为电力杆塔构成节点集合，E为电力线路构成边集合，不同于传统CPP，本文结合巡检体对输电线路协同巡检的特点，首先巡检体从某一奇点出发对输电网开始巡检，最终以某一奇点结束巡检，即“一笔画问题”，其次巡检体在输电线路某一奇点完成巡检作业可以紧接着直接前往输电线路下一个奇点开始巡检作业。改进CPP 求解路线图如图4 所示。而改进的中国邮递员问题寻找最短巡检路线归结为图论［17］问题。

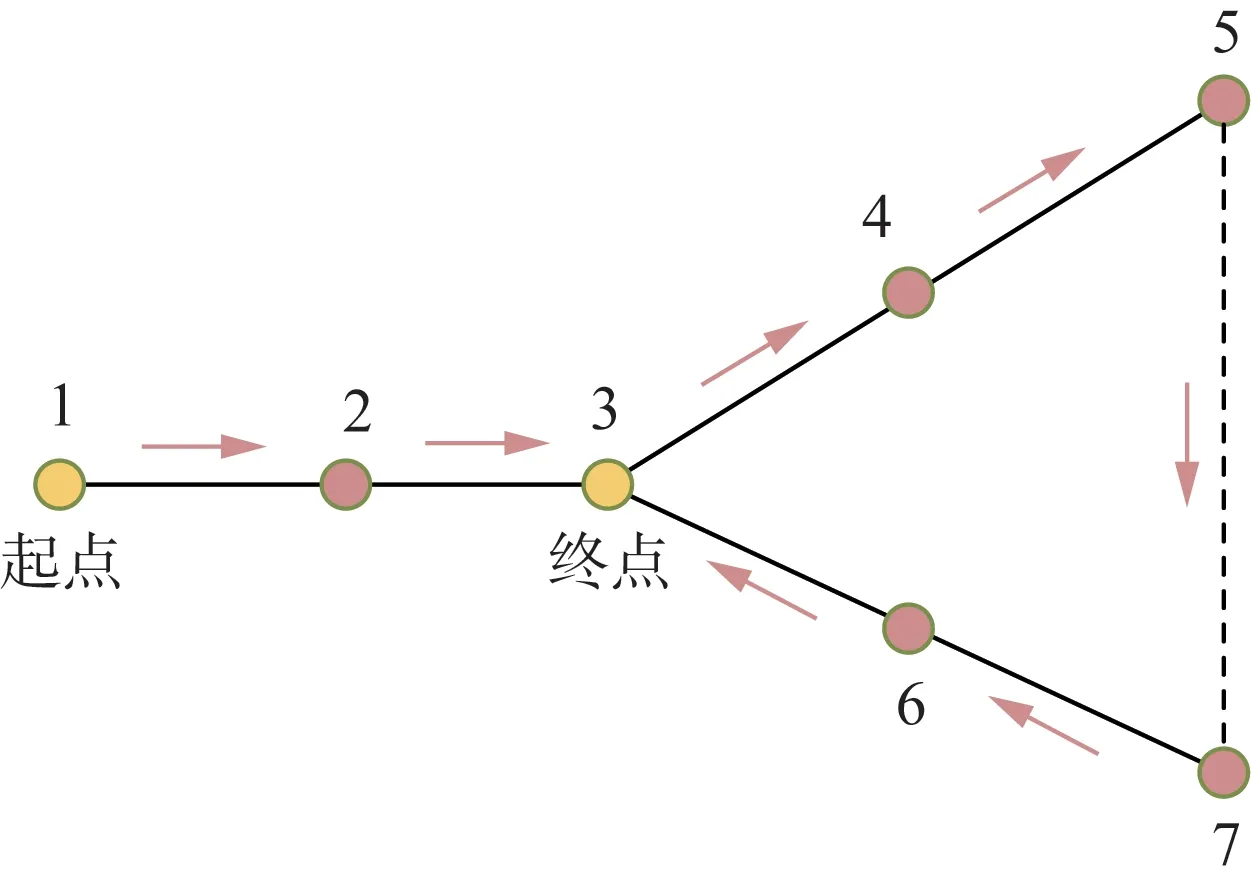
图4 改进CPP示意图Fig.4 Schematic diagram of improved CPP

给定无向连通图G(V，E)，设奇点集合为V1，奇点Vi、Vj之间本身存在连接边eij，则eij至多添加一条新边，且=ω(eij)。奇点Vi、Vj之间本身不存在连接边eij，则Vi、Vj之间至多添加一条新边为Vi、Vj之间的欧式距离，得到新图G'(V，E')，求使图G'中保留两个指定特殊奇点且总权值最小的欧拉通路，E'为通路集合，其中两个指定特殊奇点为欧拉通路的起点和终点。

最后采用最小权匹配算法和Fleury 算法结合求解该问题，下面对两算法进行介绍。

1）最小权匹配算法

CPP最早研究方法是奇偶点作业法［18］，但是对于本文比较大的输电线路网络等效图，算法的时间复杂度过大。结合图论中二分匹配［19］，通过对边权值取反将最大权匹配问题转换为最小权匹配问题以完成非欧拉图向欧拉图的转换。

2）Fleury算法

在上述已求得最小权半欧拉图的前提下，接下来改进CPP 需求该半欧拉图的欧拉通路，本文采用Fleury 算法，该算法既可以用来求欧拉图的欧拉回路也可以求本文半欧拉图的欧拉通路。

设G'(V，E')为无向半欧拉图，Fleury 算法求解过程参考文献［20-21］。

2.2 离散杆塔分割弧算法

结合本文多目标巡检特点，本文以电力杆塔作为输电线路上的离散点来分析协同巡检问题，提出了离散杆塔分割弧算法。该算法由于采用杆塔作为离散点相较于常规的取线路离散点方法（二分法、等距法等）更为密集，从而进一步扩大了解的可行域，可以获得一个较优的初始解。

2.2.1 算法原理

在执行巡检任务的第k个巡检单元中，若k为空载巡检单元，则该单元耗时为巡检车行驶时间。若k为负载巡检单元，则该单元内无人机需要执行巡检任务，设无人机在该单元飞入飞出输电网的位置点分别为a、b，设x为输电线路任意点，若该点为杆塔点，对应的杆塔巡检顺序值点为β(x)，若该点为线路点，对应的杆塔巡检顺序值点为[β(x)-，β(x)+]。已知巡检车停靠点集合为Vp={p1，p1，…，pn}；Lab为a、b之间的输电线路长度；为x到停靠点之间的距离；为停靠点pi和pj之间的距离；Tg为无人机精细化巡检杆塔耗费时长。构造函数H(x)，表示输电线路上任意位置点x到离该位置点最近的巡检车停靠点px的距离，用数学公式表示为：

采用贪心策略判断：

1）b为杆塔点

（1）与下一待巡检杆塔无电力线路连接

若满足：

则无人机从b直接返航，由巡检车运往下一负载巡检单元。

若满足：

则无人机不巡检杆塔b直接返航。

（2）与下一待巡检杆塔有电力线路连接

同式（16）及其结论。

2）b为线路点

则满足：

2.2.2 算法求解策略

从起始杆塔开始执行巡检任务，针对电力线路和电力杆塔联合巡检的特点，结合上述贪心判断思想，直至完成所有巡检任务。算法流程图如图5所示。

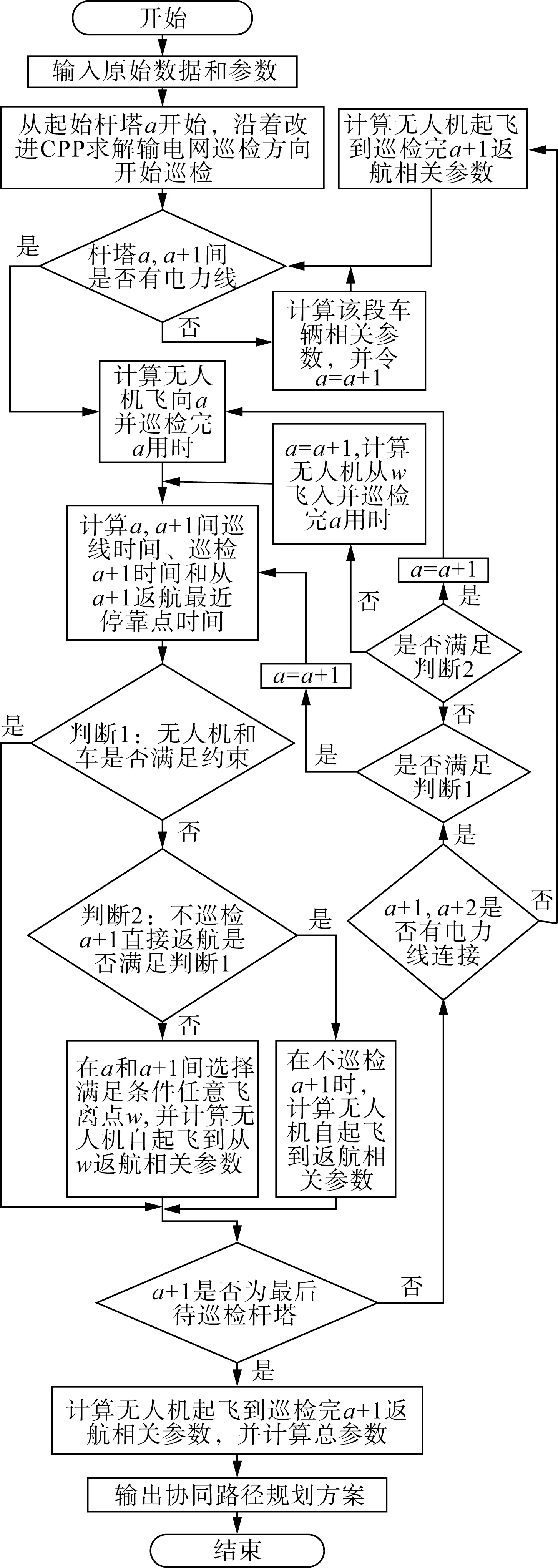
图5 离散杆塔分割弧算法流程图Fig.5 Flow chart of discrete tower segmentation arc algorithm

2.3 优化求解算法

上述算法已求得的较优解仍然有优化空间，由于模拟退火算法具有较好的全局收敛性，当温度较高时，算法跳出局部最优空间范围能力强，随着温度下降，算法跳出局部最优空间的能力逐渐减弱。最终算法在温度趋向于最低临界值时趋向于全局最优解［22］，本文采用该算法对初始解进一步优化，算法步骤参考文献［23-25］。

由于本文研究的电力巡检问题的特殊性，一些传统路径规划算子无法适用，因此本文结合无人机巡检的相关特点，提出了小规模组合算子。

1）邻近杆塔交换算子

邻近杆塔交换算子是指无人机的飞入点或飞出点与邻近杆塔在某区间范围内进行交换。

2）邻近巡检车停靠点交换算子

邻近巡检车停靠点交换算子是指改变在当前最优条件下采取最近停靠点的策略，调整为可以选取次最近停靠点。

3 算例分析

算例选取某市长45 km、宽30 km 的110 kV 输电线路运维区域，如图6 所示。运维区域的待巡检目标为电力线路和电力杆塔，其中电力杆塔195基。该运维区域的输电线路抽象为图论问题含有8个奇点，根据该运维区域实际路网图中适合无人机放飞和回收的地点选取出35 个合适的运维车停靠点，编号为1—35。

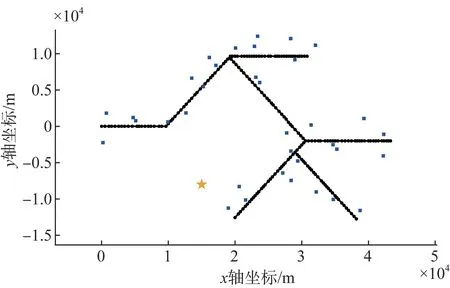
图6 运维区域Fig.6 Operation and maintenance area

3.1 算例参数设置

电力巡检相关参数如表1所示。

表1 电力巡检参数表Tab.1 Parameters table of power inspection

3.2 不同场景下不同策略对结果的影响

为了验证模型的合理性和有效性，本文考虑两种策略在3 个场景下的结果对比，场景1 为恶劣山路，场景2为乡间小路，场景3为平坦公路，3个场景主要对巡检车行驶速度产生影响；策略1 为考虑无人机悬停，策略2 为不考虑无人机悬停，对比结果如表2所示。

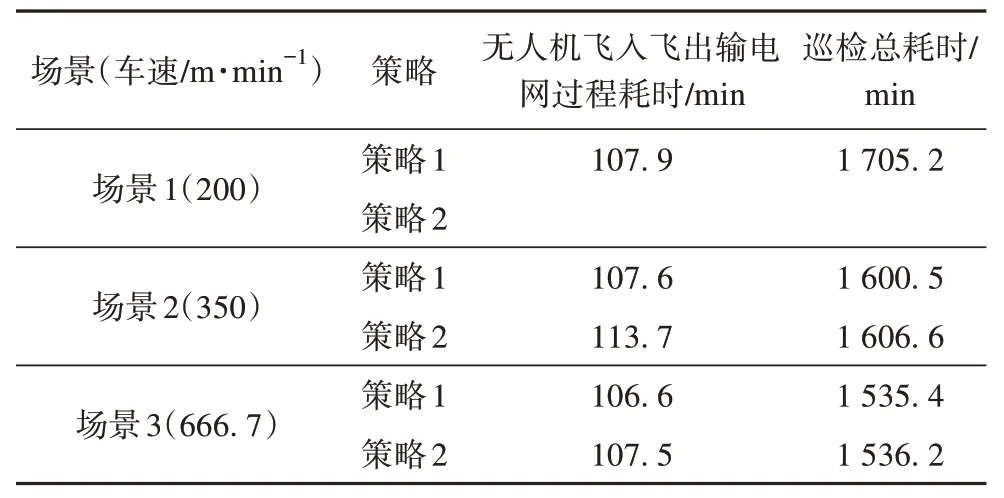
表2 多场景不同策略方案结果对比Tab.2 Comparison of the results of different strategies for multiple scenarios

由表2 可知，场景1 采用策略2 会造成该场景下无法完成巡检任务，即无可行解；场景2 采用策略1 相较于策略2 在巡检总耗时和无人机飞入飞出输电网过程耗时缩短了6.1 min，换算成距离为3.05 km。场景3 中，两种策略对两类耗时的影响差异可忽略不计，造成该现象的主要原因是随着巡检车的速度不断提升，巡检车提前到达停靠点等待无人机的概率不断增大。3 个场景在策略1 的情况下无人机飞入飞出过程耗时接近是由于无人机在巡检中根据离散杆塔分割弧算法贪婪判断过程中均可满足判断条件，导致最终终止判断位置接近，削弱了巡检车速度对最终解的影响；在策略2 的情况下随着不同场景巡检车速度的提升，开始出现可行解/可行解变小，并逐渐趋于策略1的可行解。综合3 个场景下策略1 和策略2 对解的影响，策略1 避免了极端场景下巡检过程中不可行解的出现，扩大了解的范围，缩短了无人机的飞入飞出时间，进而减少了巡检总耗时，综上可知策略1优于策略2。

3.3 车载无人机协同巡检路径规划结果

由于篇幅有限，下文基于场景3 策略1 下协同巡检路径规划结果进一步分析，并探究自然灾害（暴雨、台风）等条件下，道路损坏导致无法按照原先正常优化路线到达下一停靠点的情况，说明优化算法的有效性和普适性。

假设自然灾害条件下，车辆停靠点3、15、16、19、24、25、31、34无法满足停靠要求，需重新规划巡检路线。基于改进CPP 和离散杆塔分割弧的递推算法的协同路径初步规划方案的遍历过程对比如图7 所示，由图可知正常情况下最小巡检总耗时为1 535 min，自然灾害条件下最小巡检总耗时为1 571 min，两者对应的巡检路径规划图如图8 所示，相比于正常条件下的路线，自然灾害条件下通过调整车辆停靠点和无人机飞入飞出点来协同优化巡检路线。

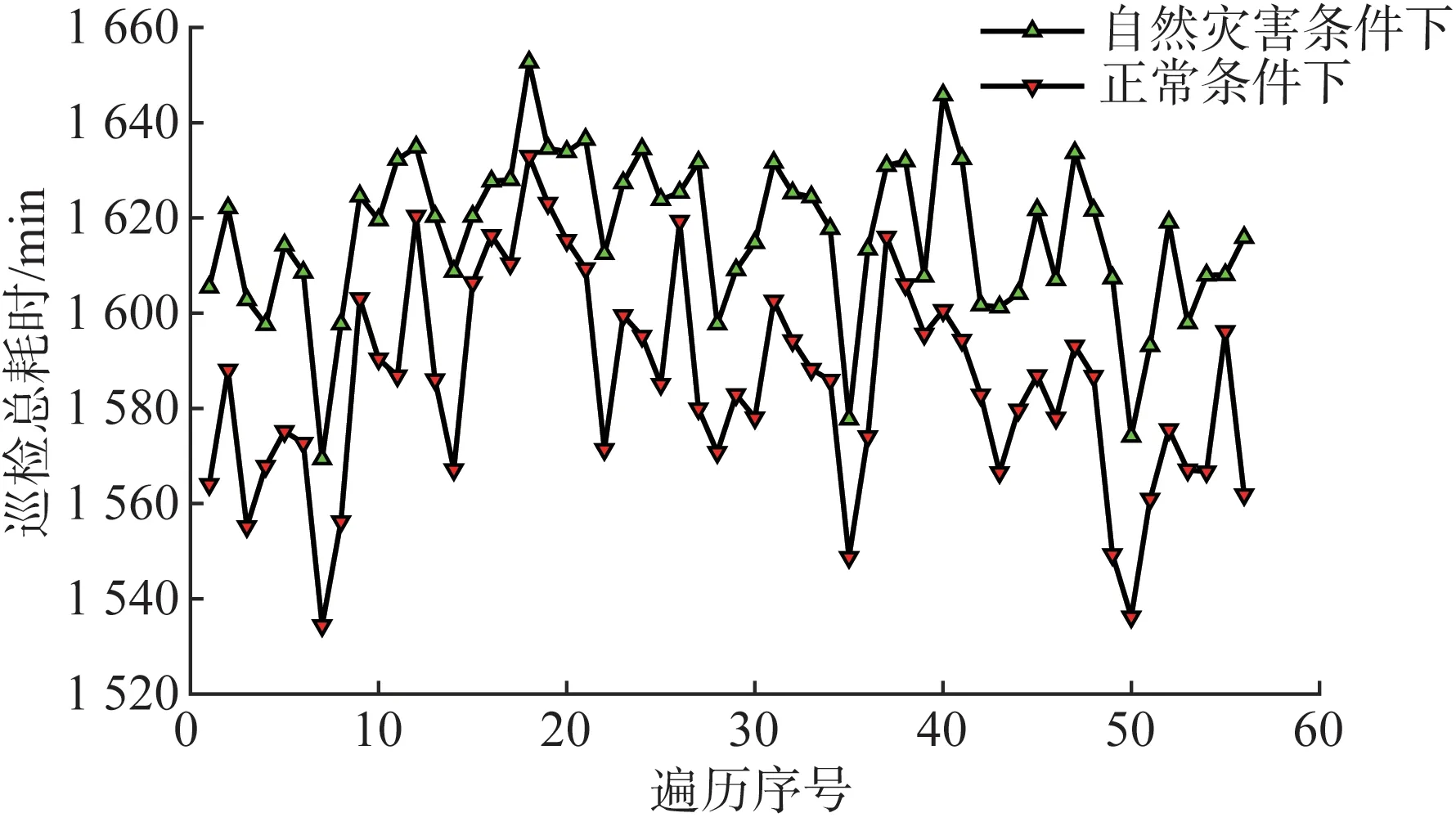
图7 初步规划方案遍历结果图Fig.7 Preliminary planning scheme traversal result map

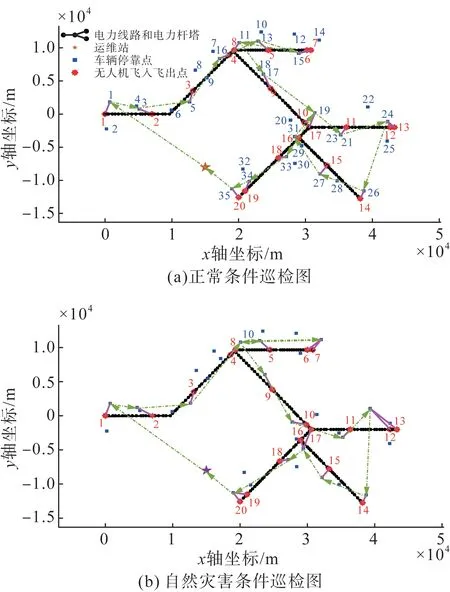
图8 协同巡检路径规划图Fig.8 Planning diagram of cooperative inspection path

为了进一步验证模拟退火算法的有效性，下文在图8（a）（下文称方案1）的基础上优化协同巡检路线，优化后的路径规划方案称为方案2。路径优化图如图9所示。

图9 协同巡检路径优化图Fig.9 Cooperative inspection path optimization diagram

图8 和图9 中绿色箭头代表巡检车行驶路线，蓝色数字代表巡检车停靠点序号。红色线段代表无人机飞入飞出路线，红色数字代表无人机飞入飞出点顺序。方案1 是车载无人机从运维站出发以某一杆塔奇点作为巡检输电网出发点再以之外某一杆塔奇点作为返回点返回运维站中最优的规划结果，负载巡检单元段内无人机和巡检车配合执行巡检作业任务，例如巡检飞入飞出点1 至7 间的输电线路，空载巡检单元内，巡检车运载无人机前往下一待巡检杆塔，例如运维站—停靠点2、停靠点15—停靠点11。本文算法保证了无人机每次巡检为最大续航时间，因此确定了最优情况下的无人机飞入飞出输电网的最少次数，在保证最优飞入飞出次数的前提下，方案2 通过领域动作对方案1 的飞入飞出点和巡检车停靠点进行调整，由图7 可知，方案2 在保证每个负载巡检段内的首尾无人机飞入飞出点不变的前提下，在满足无人机和车辆相关约束条件的前提下，对飞入飞出点和停靠点做了不同限度的调整，调整效果总体上是趋于无人机飞入飞出输电网过程时间更短和巡检车行驶时间更短，方案2 和方案1各巡检单元内用时对比如图10所示。

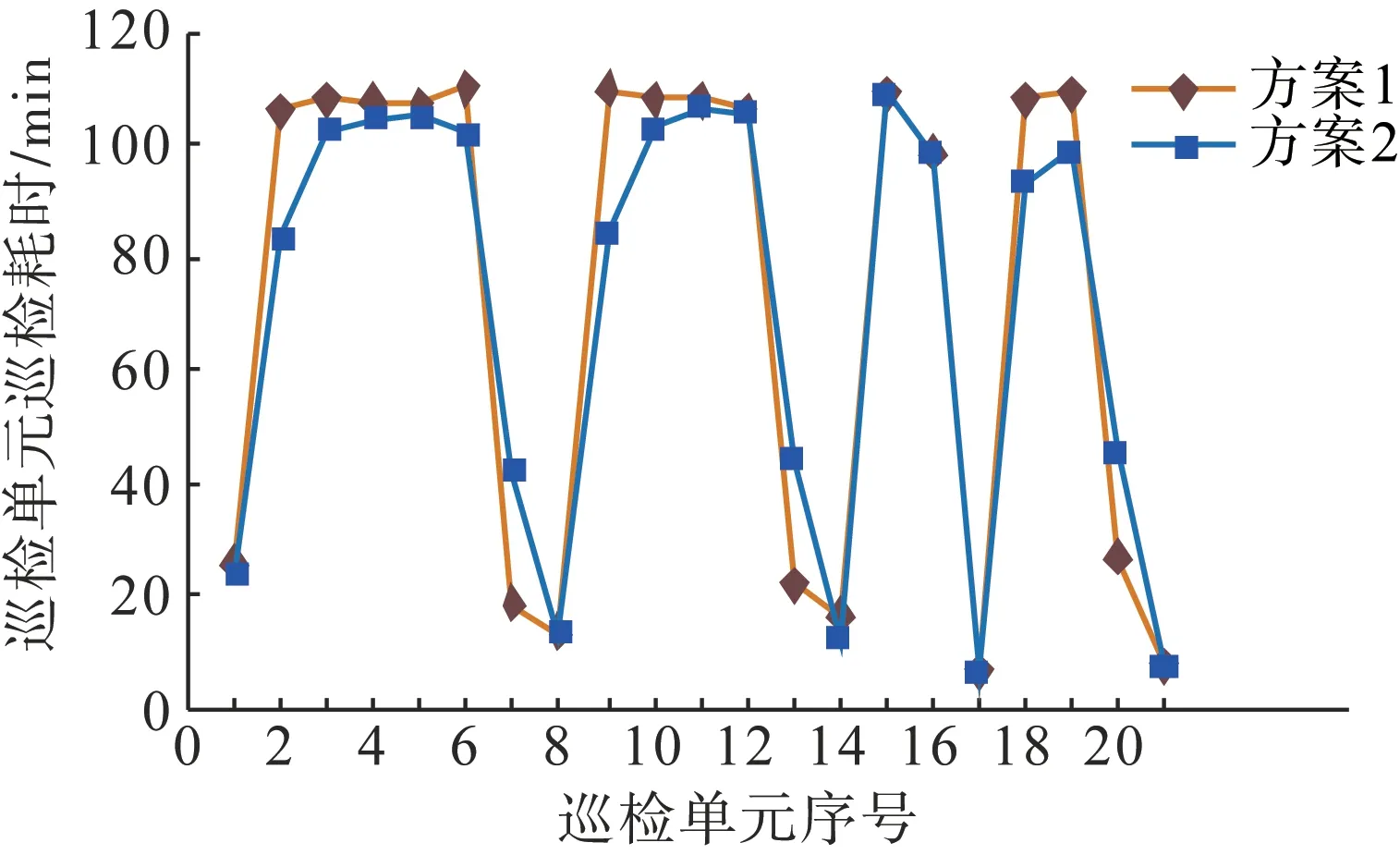
图10 方案1和方案2各巡检单元用时对比Fig.10 Comparison of the time spent on each inspection unit for Scenario 1 and Scenario 2

由图10可知，各巡检单元耗时方案2总体上相较于方案1 得到的优化，少数巡检单元例如巡检单元7（对应飞入飞出点6—7），巡检单元13，巡检单元20，三者情况相同，由于为了满足本巡检单元段内其他巡检单元的相关约束，为总体优化提供优化空间，作出局部牺牲，旨在缩短整体巡检时间。巡检单元15（对应飞入飞出点14—15）、16、17、21已无优化空间，所以两方案保持一致。两方案总体耗时对比如表3所示。

表3 两方案耗时对比Tab.3 Comparison of the parameters and indicators of the two solutions

由表3 可知。方案2 比方案1 的总耗时缩短了41 min。其中总耗时包括固定巡检任务耗时和非固定巡检任务耗时，固定巡检任务耗时指的是输电线路中所有杆塔和电力线路巡检耗时，该耗时不可优化，本文的非固定巡检任务耗时包括巡检车在空载巡检单元的行驶时间和无人机飞入飞出输电网过程中飞行用时，该耗时可优化。方案2 的可优化巡检耗时在方案1 的基础上提升了23.3%，证明了优化算法的可行性和有效性。

4 结论

针对已有研究主要考虑单目标电力巡检以及实际场景下无人机可悬停等待这一情形考虑的缺乏，本文考虑了包含电力杆塔和电力线路的多目标联合电力巡检并以车载无人机协同电力巡检任务总用时最小作为优化目标，根据 “图论”相关理论提出了一种面向电力巡检实际场景的多目标联合巡检的车机协同电力巡检协同路径规划模型，并结合相关算法对其进行求解，通过算例验证得出如下结论。

1）运用本文提出的改进CPP 和离散杆塔分割弧算法可以快速得到一个较优协同路径规划方案，该方案可快速地为电力公司电力巡检作业提供一个实用且有效的车机协同巡检路径规划方案。

2）通过对比不同场景下不同策略，可以得出考虑无人机悬停时相较于传统情况适应场景更广，解的质量更高更优。通过探究自然灾害下的优化路线，进一步验证了算法的普适性和有效性。

3）在初始优化方案的基础上结合本文提出的模拟退火算法得到的优化方案可以有效地缩短可优化耗时，具有较高的现实意义。

4）本文把巡检车行驶路径简化为节点路由问题研究，具体实际路网问题在此基础上进一步研究。