非接触式交流电压探头设计与电压测量方法

李嘉贤，刘灏，付宇，毕天姝

（1.新能源电力系统全国重点实验室（华北电力大学），北京 102206；2.贵州电网有限责任公司电力科学研究院，贵阳 550002）

0 引言

随着分布式电源的快速发展，配电网特性愈发复杂，传统依赖建模的分析方法愈发困难［1-2］。而实时、准确的同步测量为配电网监测、分析与控制提供了新的思路［3-7］。然而，配电网的海量测点与传统电压互感器（potentil transformer，PT）的制造、安装成本存在矛盾，限制了测点数量。非接触式电压传感器无需直接接触待测物体，而是利用待测物体周围的电场作为媒介逆向计算电压，在牺牲精度的同时降低了对绝缘的要求，从而降低了制造成本并提高了安装便捷性，是其在配电网广泛布点的现实基础。

绝缘导线是典型的电能传输载体，不同于裸露导体，导线外层绝缘材料的介电常数远大于空气，能够有效预防人员触电与设备短路问题，同时也在很大程度上抑制了导线在周围空间中产生的电场。所以，本文所解决的主要问题是：1）在不破坏导线绝缘层的前提下获取待测信号；2）利用采样信号逆向计算出导线电压的幅值与相角。

现有针对绝缘导线的非接触式电压测量技术普遍采用电容耦合原理设计探头来获取待测电压信号，利用导线的绝缘层充当电介质构建电容实现分压［8］。其主要困难之一在于输出信号对电容值的变化非常敏感，而电容值很大程度上取决于导线粗细、绝缘层厚度以及电压探头的相对位置［9-10］。

而对于逆向计算电压，当前主要有3 种思路：第一种思路是将探头固定在待测导线上，确保相对位置（即电容值）不发生变化，再利用校准的方法获得待测电压与探头输出信号之间的比例系数。文献［11］使用3 个微型平板构建电容器，紧贴目标导线以获取待测电压的变化率，对其进行数字积分来恢复信号波形。文献［12-13］将其扩展应用至多相导线的非接触式电压测量。这种方法能够计算待测电压的频率和相位，但无法直接测量电压幅值，需要在每次固定探头后利用已知电压或者接触式测量结果来校准目标电压幅值与探头输出幅值之比。

第二种思路是采用内置电压发生器生成一个已知的参考电压，将其与探头输出叠加合成一个复合电压，对该复合电压进行分析计算待测电压［14-18］。文献［14］采用快速傅里叶变换（fast Fourier transform，FFT）对复合信号进行频谱分析。文献［15］提出了一种自动平衡信号调理电路处理复合电压信号，以计算目标电压的真有效值。文献［16］中提出了一种基于双斜率技术的数字化仪，但要求参考电压的频率是待测电压的整数倍。文献［17-18］利用带通滤波器分离复合信号，仍需要一个初始校准来获得输入信号和输出信号之间的比例系数。

第三种思路是利用内置电压发生器还原出待测电压。文献［19］将金属极板靠近待测导线获取信号，并采用FFT 进行频谱分析计算出该信号的频率、相位参数，根据这些参数在装置内部生成一个参考电压，并检测回路电流，若电流小于允许范围，则判定生成的参考电压等于待测电压。该方案要求电压发生器能够准确复制出目标电压，实现起来较为困难。

针对绝缘导线的非接触式电压测量问题，本文利用金属薄膜与绝缘薄膜缠绕导线构建了非接触式交流电压探头，分析了探头接入采样电路后的等效电路图与相量图，提出了一种基于双探头的逆向求解电压方法，无需破坏导线绝缘层即可测量电压的幅值、相角、频率。

1 导线电场建模及其特性分析

1.1 同心双圆柱电容结构及其等效电路

导线的绝缘层具备极大的电阻，在保障人身与设备安全的同时，给电压测量带来了困难。电容作为电压与电场之间的桥梁，是跨过绝缘层引出信号的有效手段。本文采用金属薄膜与绝缘薄膜缠绕导线构建了双层柱状电容结构，其横截面如图1所示。

图1 导线横截面示意图Fig.1 Schematic diagram of wire cross section

图中结构内部电场可由式（1）表示。

式中：E为电场强度，方向为径向；k为单位长度上的电荷量；ε为绝缘材料的介电常数；r为半径；R0为导线内部导体半径；R1为导线外部半径；R2为输出金属薄膜外部半径；R3为绝缘薄膜外部半径。

图1中的Ui和Uo分别表示导线内部待测电压，即探头的输入电压和两层金属薄膜之间的输出电压。它们可由电场直接积分得到，如式（2）—（3）所示。

图1 双层电容结构可简化为两个电容串联，其等效电路如图2 所示。其中，Co为接地金属薄膜与输出金属薄膜之间的等效电容，Ci为输出金属薄膜与待测导线之间的等效电容。

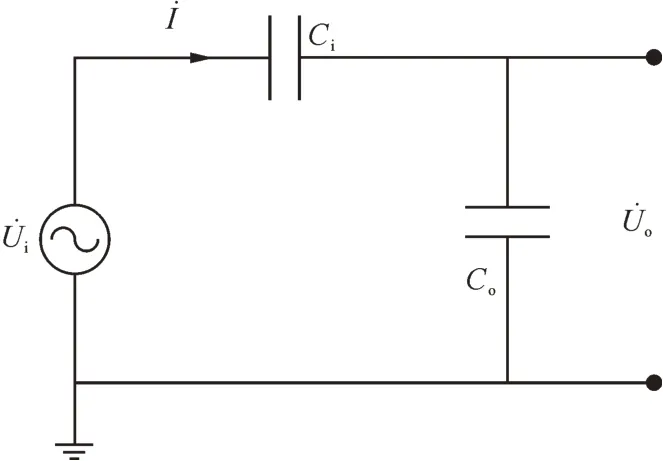
图2 等效电路图Fig.2 Equivalent circuit diagram

图2两个电容的电容值如式（4）所示。

式中：ε1与ε2为介电常数；L为圆柱电容器的长度。

图2电路对应的电压电流相量图如图3所示。

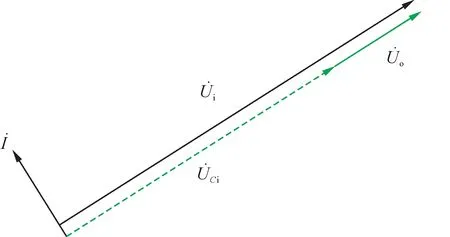
图3 电压探头相量图Fig.3 Phasor diagram of voltage probe

式中：Ui与Uo为电压幅值；φi与φo为电压相角。

从上述分析可以看出，所提同心双圆柱结构与传统的电容分压器在原理上相同，但电容分压器的内外电容值是已知的，所以可以对二次侧输出电压=Uo∠φo进行采样，利用式（5）计算出一次侧输入电压的幅值Uo与相角φo。但在对绝缘导线进行非接触式电压测量时，导线内部导体与输出金属薄膜之间的电容Ci无法测量且无法利用式（4）计算得到，所以无法利用输出电压和式（5）计算输入电压。

1.2 采样电路的影响

非接触式电压测量的困难不仅仅在于内部电容Ci未知，还受到采样电路对探头的影响。为了获得探头输出电压，采样过程是不可或缺的，而问题恰恰在于采样电路不可避免地需要从探头中获取电流。不同于接触式测量，非接触式电压探头从待测电路中获取的电流非常微弱，导致采样电路获取的电流占比无法忽略。电压探头接入采样电路后，等效电路图由图2 变为图4，相当于在输出电容Co上并联了一个采样电阻。

图4 考虑采样电路时的等效电路图Fig.4 Equivalent circuit diagram considering sampling circuit

此时，二次侧的输出阻抗不再为纯容性，输入电压和输出电压的相位不再相同，相量图由图3 变为图5。

图5 电压探头接入采样电路后的相量图Fig.5 Phasor diagram of voltage probe with sampling circuit

图5中电压与电流满足如下关系。

2 基于双探头的导线电压测量方法

从第一节的分析可知，导线内部导体与探头之间的电容值Ci未知，使得双电容分压情况不确定，加上采样电路从探头获取的电流不可忽略，为电压计算带来了更大的困难。为了求解待测电压，本文提出了一种基于双探头的非接触式电压测量方法。

考虑两个长度不同的探头，安装在同一根绝缘导线上，由于探头的内、外层电容值不同，其内部电压分布相量图如图6所示。

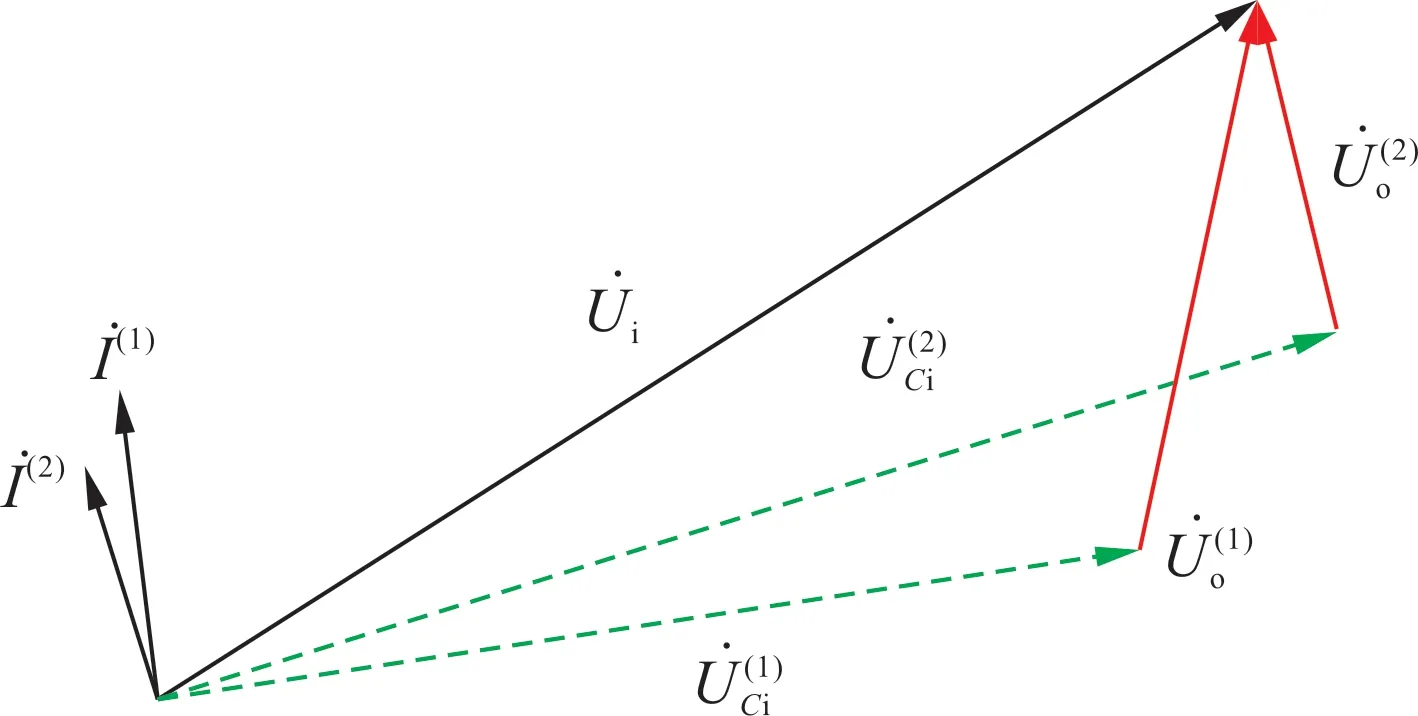
图6 双电压探头相量图Fig.6 Phasor diagram of double voltage probes

图6 中上标（1）代表1 号探头，上标（2）代表2号探头。显然，电流可以利用输出电压和输出阻抗来计算，如式（7）所示。

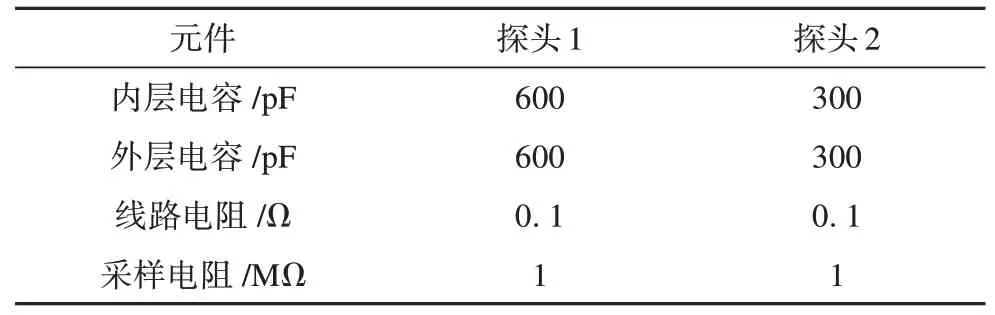
表1 元件参数Tab.1 Parameters of components

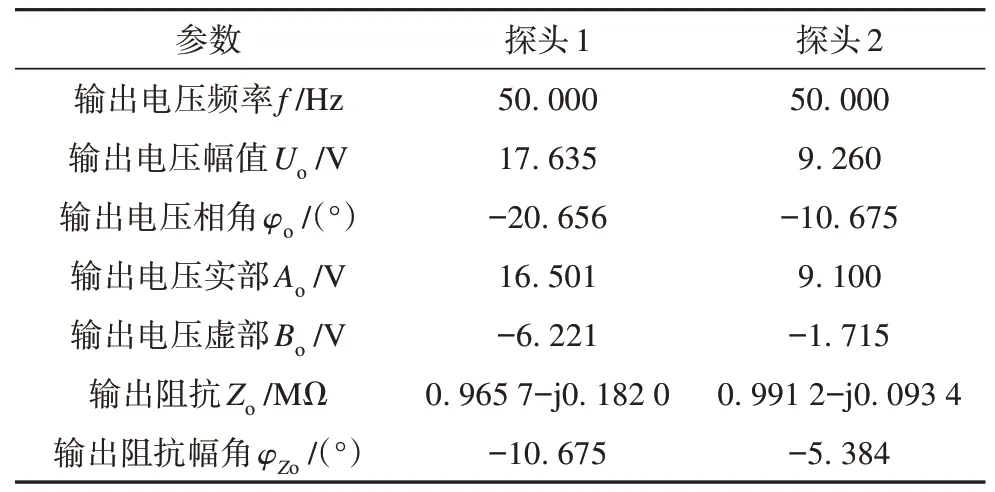
表2 输出参数计算值Tab.2 Calculated values of output voltage parameters

虽然内层电容Ci1与Ci2未知，但内层电容两端的电压相位必然滞后电流π/2，如式（8）所示。

电压相量是一个复数，有幅值相角和实部虚部两种表示方式，如式（10）所示。

进而可以求得待测电压的幅值Ui与相角φi，如式（12）所示。

需要注意的是，式（11）中的正切值在某些角度时较小，需要将输入电压旋转一定角度以避免分母为0，待求得相角φi后再逆向旋转还原。此外式（12）中的反正切函数存在双值，判断的原则是输入电压与输出电压相角不应相差90 °以上。

综上所述，所提绝缘导线非接触式电压测量方法的流程图如图7所示。

图7 非接触式电压测量方法流程图Fig.7 Flow chart of the non-contact voltage measurement method

3 仿真分析

3.1 基本测试

为了验证所提方法的有效性，使用Simulink 软件进行了仿真分析，电路如图8所示。

图8 仿真电路图Fig.8 Simulation circuit

电源电压瞬时值ui（t）与相量如式（13）所示。

式中：t为时间；电压频率为50 Hz。

图8中元件参数如表1所示。

仿真得到的输入电压ui（t）和输出电压uo1（t）、uo2（t）的波形如图9所示。

可以看出，输出电压相对于输入电压存在相移。采用文献［20］中提出的方法计算出两输出电压uo1（t）和uo2（t）的频率、幅值和相角，可以计算出外部电容的容抗，进而结合采样电阻得到电路的输出阻抗Zo。计算结果如表2所示。

可以计算出内层电容两端电压相角为：

将表2 与式（14）数据代入式（11）—（12）得到待测电压幅值、相角计算值及其误差，如表3所示。

表3 待测电压计算结果Tab.3 Calculation results of the voltage to be measured

从表3可以看出，所提非接触式电压传感方法的幅值误差为0.005 1%，相角误差为-2.661 °×10-5。

3.2 噪声测试

为了模拟实际场景，在3.1 节的基础上，人为地在2个输出电压瞬时值uo1（t）和uo2（t）中加入40 dB高斯白噪声，以观察所提方法的抗噪能力。加入噪声后的待测电压幅值计算值如图10 所示，电压相角计算值如图11所示。

图10 电压幅值计算值（40 dB噪声）Fig.10 Voltage amplitude measurements with 40 dB noise

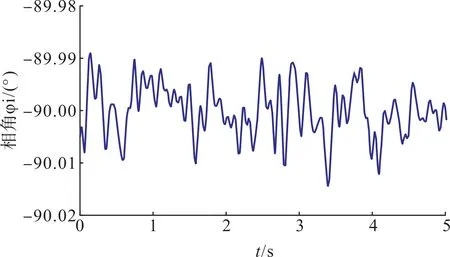
图11 电压相角计算值（40 dB噪声）Fig.11 Measurement values of voltage phase angles with 40 dB noise

可以看出，40 dB 噪声造成的幅值误差小于0.2%，相角误差小于0.02 °。

3.3 相量算法误差影响

对于不同的频率与相量算法而言，其误差特性不同。为分析所提传感方法对不同相量算法的适用性，上限为±0.1%、±0.2%、±0.3%、±0.4% 和±0.5%的随机误差被人为地添加到输出电压的幅值计算结果中。输出电压幅值计算值和待测电压幅值、相角计算结果如图12 所示。可以看出，由幅值误差在0.5%以内的相量算法造成的幅值误差在±1%以内，相角误差在±0.05 °以内。将上限为±0.01 °、±0.02 °、±0.03 °、±0.04 °和±0.05 °的随机误差添加到输出电压的相角中，输出电压相角和待测电压计算结果如图13 所示。可以看出，±0.05 ° 的相量算法误差将会导致±5%以内的幅值误差和±0.2 °以内的相位误差。

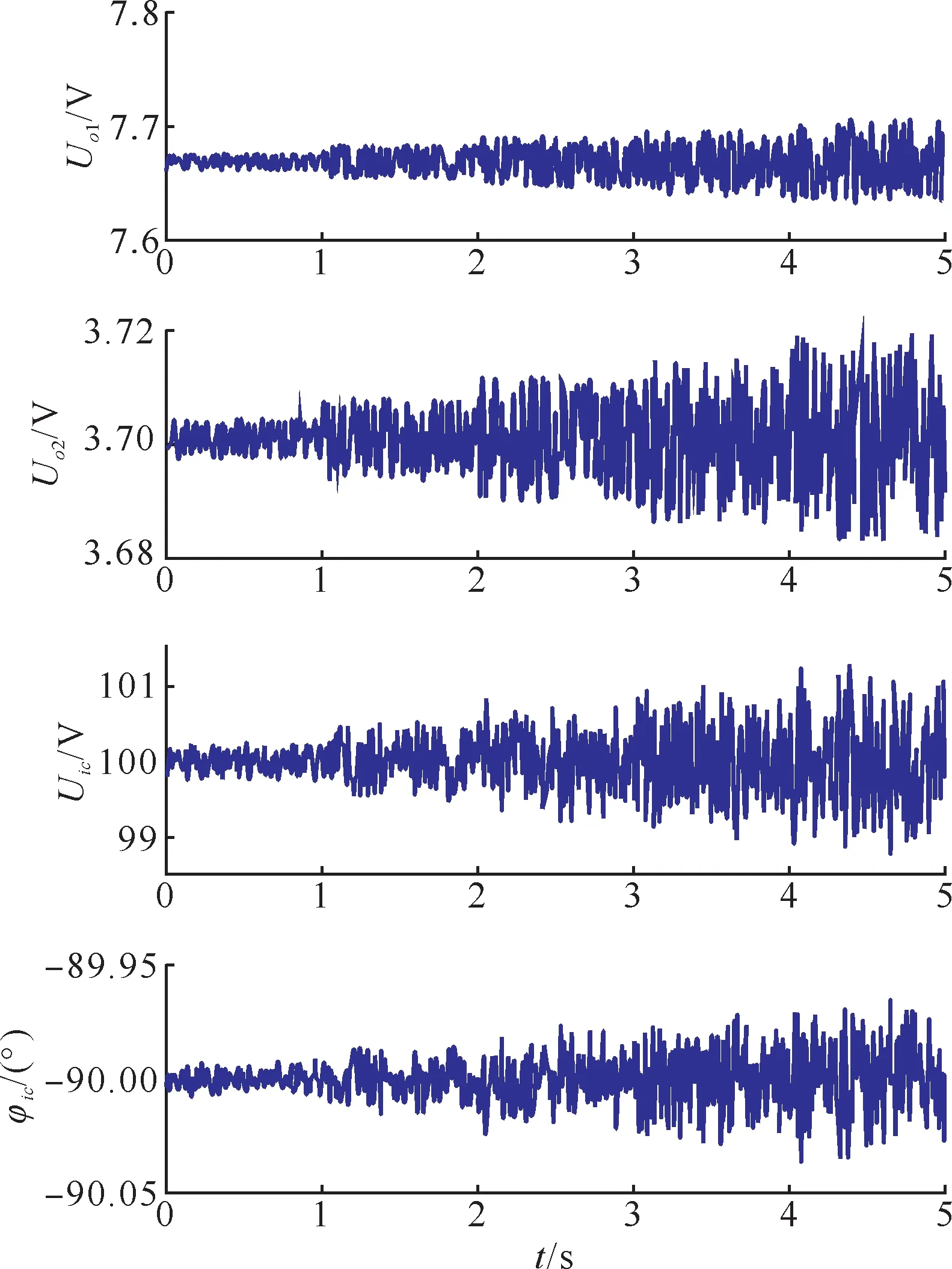
图12 输出电压幅值与待测电压幅值、相角计算值Fig.12 The output voltage amplitude and the calculated value of the voltage amplitude and phase angle to be measured

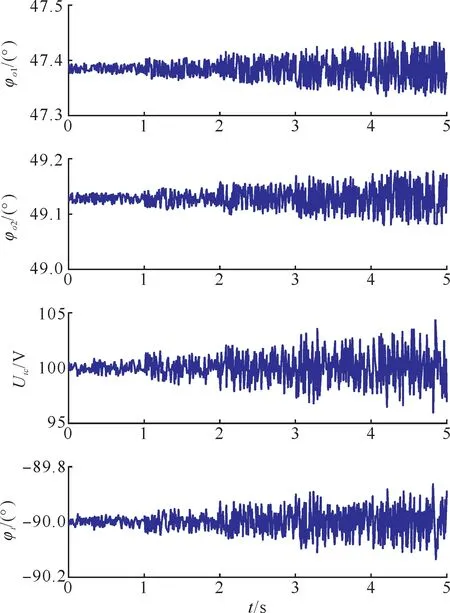
图13 输出电压相角与待测电压幅值、相角测量值Fig.13 The output voltage phase and the calculated value of the voltage amplitude and phase angle to be measured

3.4 探头电容值偏差测试

实际导线由于负载电流造成发热，使得绝缘外皮的介电常数发生变化，虽然不同材料的介电常数随温度变化特性不同，但其直接结果均为所提电压探头的内、外层电容值发生变化。为模拟导线发热对非接触式电压测量精度的影响，以表1 参数为基准改变双探头的外层电容值进行测试，结果如表4所示。

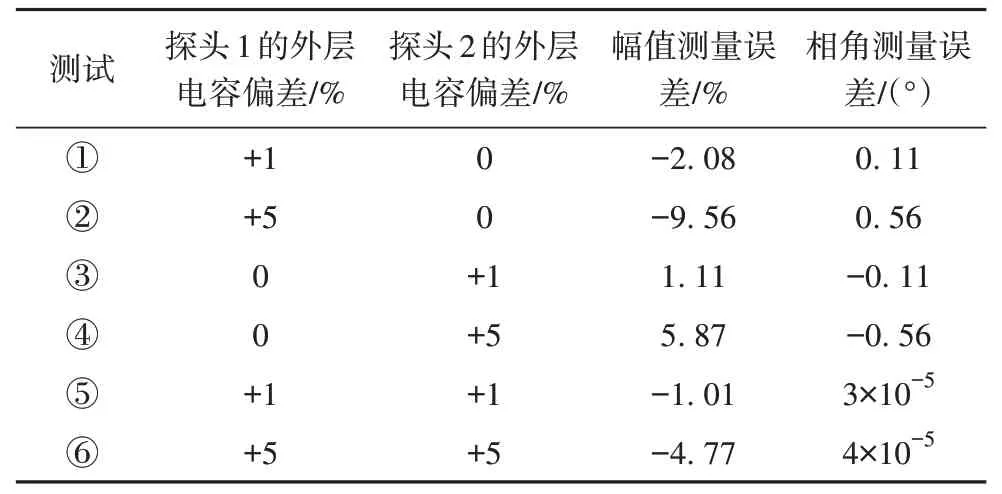
表4 探头外层电容值偏差影响测试Tab.4 Measurement errors caused by capacitance value offset

从表4 可以看出，对比由于探头电容值的相对偏差会造成电压幅值和相角的测量误差，其误差传递近似呈线性关系。对比测试①、③以及测试②、④发现，由于探头1 本身电容值较大，其相对偏差造成的测量误差也较大。观察测试⑤、⑥发现，两个探头电容值相对偏差程度相同时，不影响电压相角计算结果。

4 实验测试

为验证所提非接触式电压传感方法的实用性，搭建了实验平台对其进行验证，实验架构示意图如图14所示。

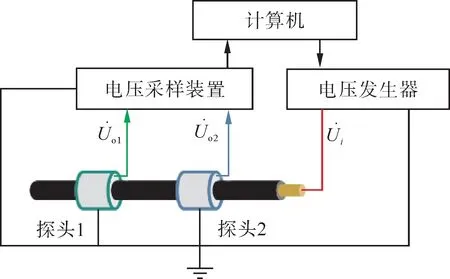
图14 实验架构示意图Fig.14 Schematic diagram of test architecture

利用计算机控制电压发生器生成一个频率、幅值和相角皆已知的电压，将该电压加在圆柱形铜管上，铜管外层缠绕绝缘胶带以模拟绝缘导线。在模拟导线外层缠绕宽度不同的铝箔构建两个探头。对探头输出电压进行采样，用所提方法得到输入电压的计算值，将计算结果与设置的已知参数进行对比得到电压测量误差，测试平台照片如图15所示。

图15 测试平台照片Fig.15 Photo of test platform

图15 中电压发生器为Omicron CMC 256 plus，电压采集装置为NI Compact-RIO 9039，电压采集板卡为NI 9239，量程为10 V，输入电阻为1 MΩ。输入电压瞬时值ui（t）与相量如式（15）所示。

式中：t为时间；电压频率为50Hz。

电容表测量1号探头外层电容如图16所示，两个探头参数测量结果如表5所示。

表5 元件参数Tab.5 Parameters of sensors

图16 探头外层电容测量Fig.16 Measurement of sensor outer capacitance

待测输入电压和两个探头的输出电压的采样波形如图17 所示。两个探头输出电压的频率计算值如图18所示。将频率计算值结合表4中的外层电容值与采样电阻可以得到两个输出阻抗Zo1与Zo2。两个探头输出电压的幅值Uo1、Uo2与相角φo1、φo2计算结果如图19所示。

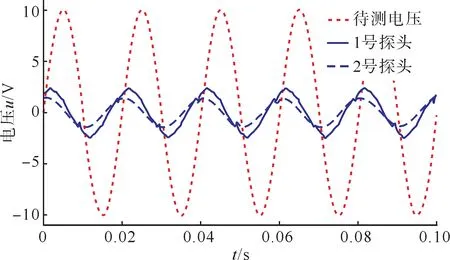
图17 输入电压与输出电压采样波形Fig.17 Waveforms of input voltages and output voltages.

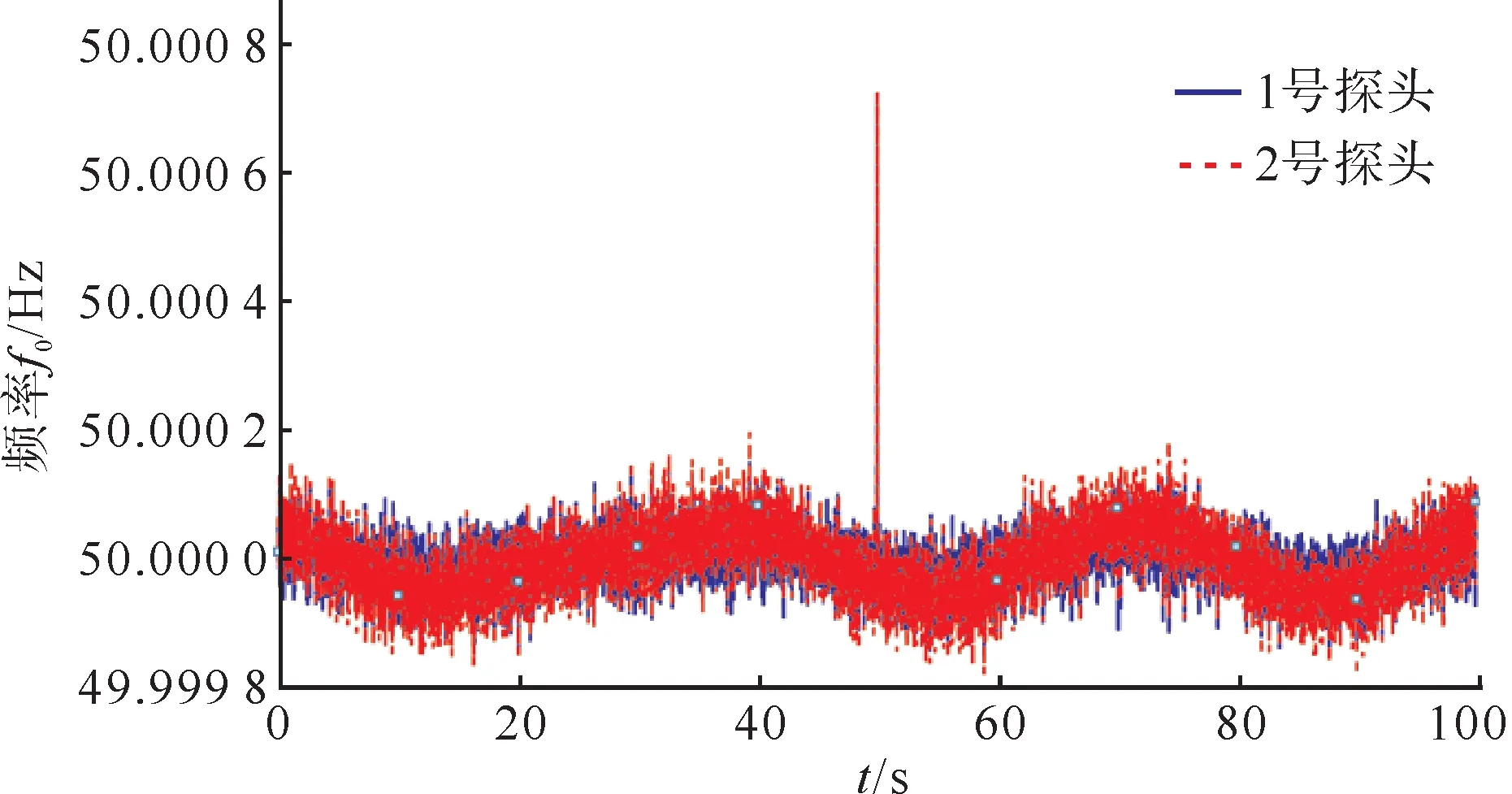
图18 输出电压频率测量值Fig.18 Measurement values of output voltage frequencies

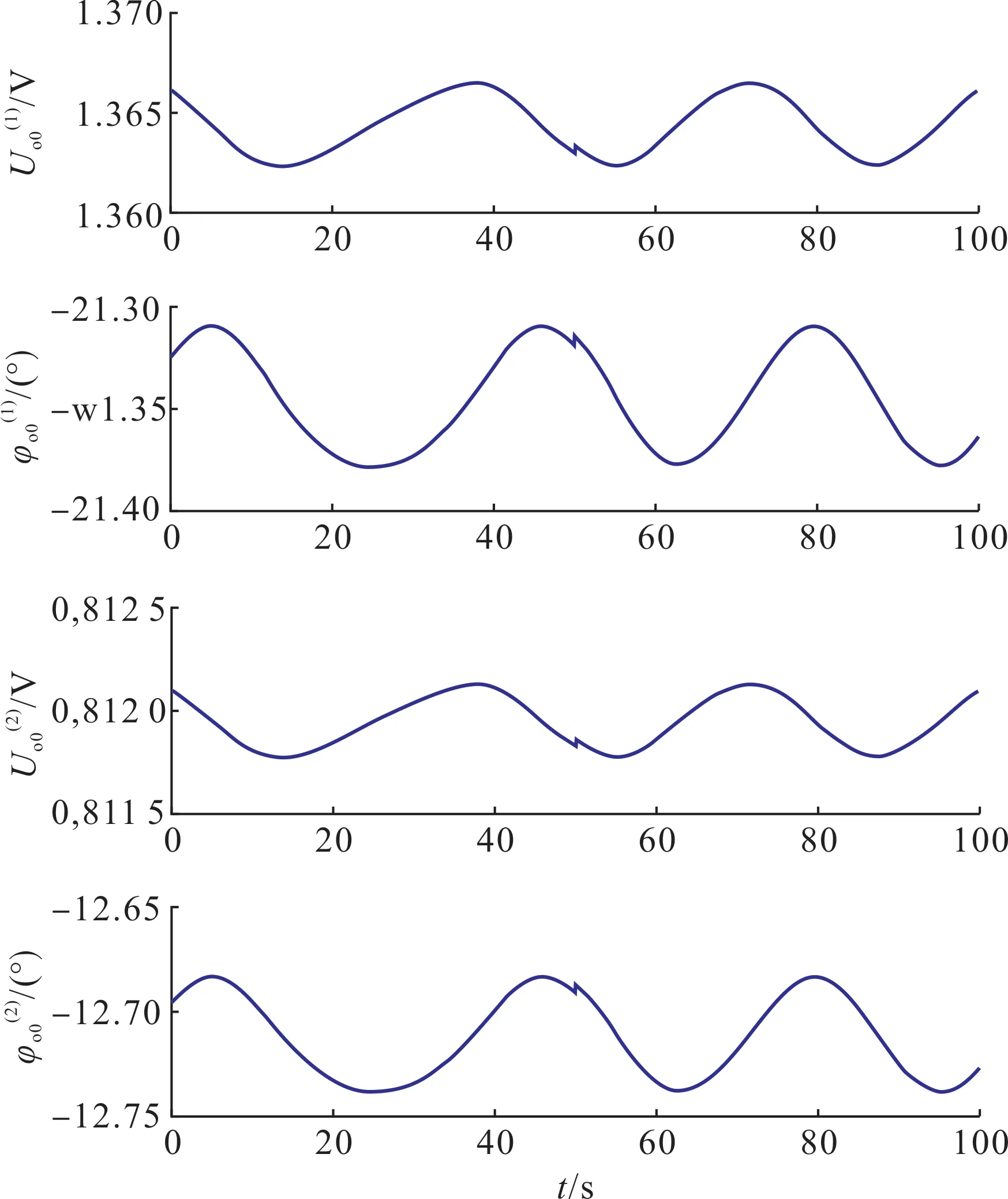
图19 探头输出电压的幅值与相角Fig.19 Amplitudes and phases of probe output voltage

可以看出，受到环境电场影响，探头输出电压的幅值、相角均存在周期性波动，并且大约在50 s处存在一个微小的扰动。

将探头输出电压相量测量值代入式（11）—（12），可逆向计算出输入电压的幅值、相角，如图20—21所示。

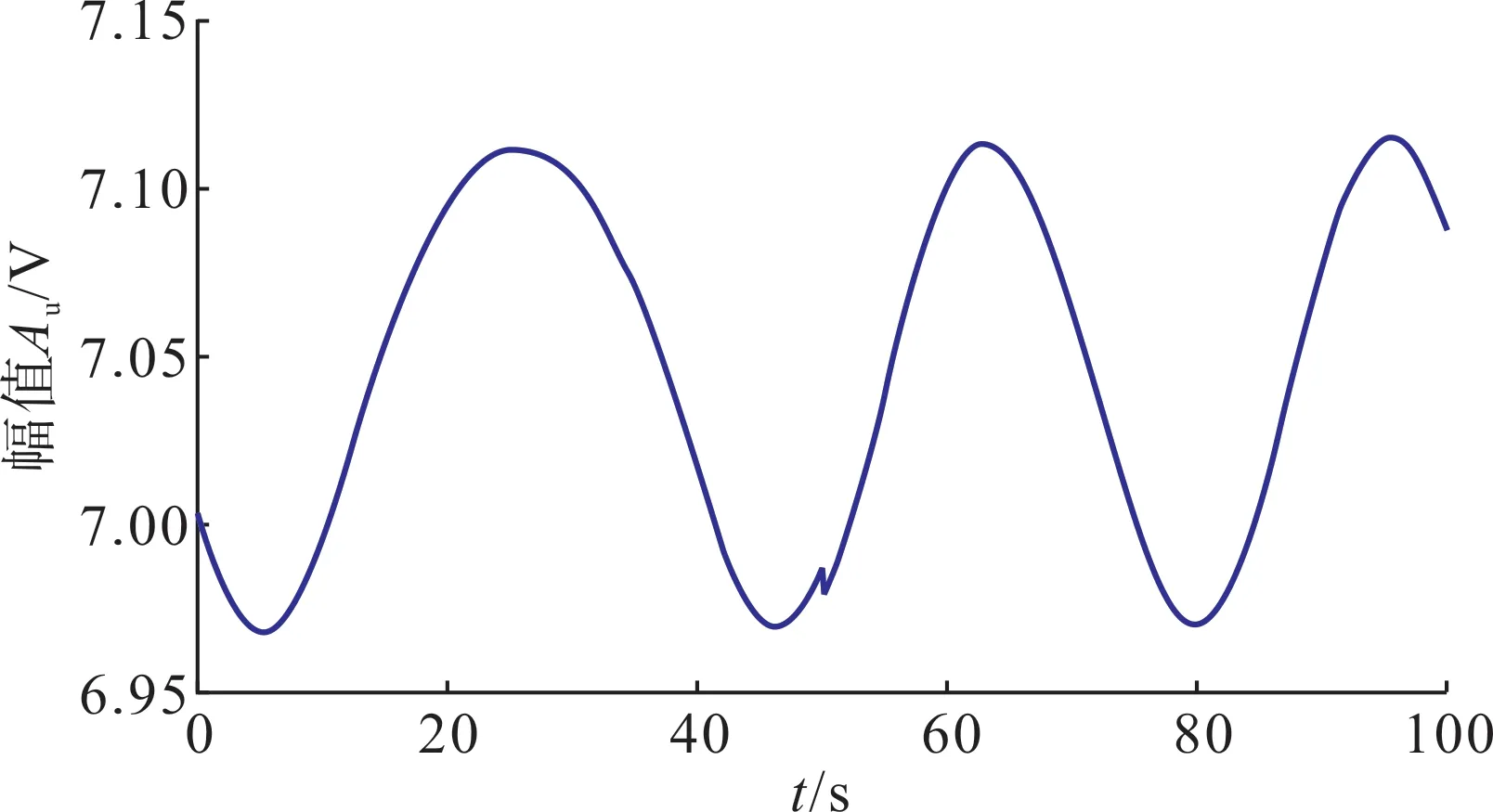
图20 电压幅值测量值Fig.20 Measurement values of target voltage amplitude

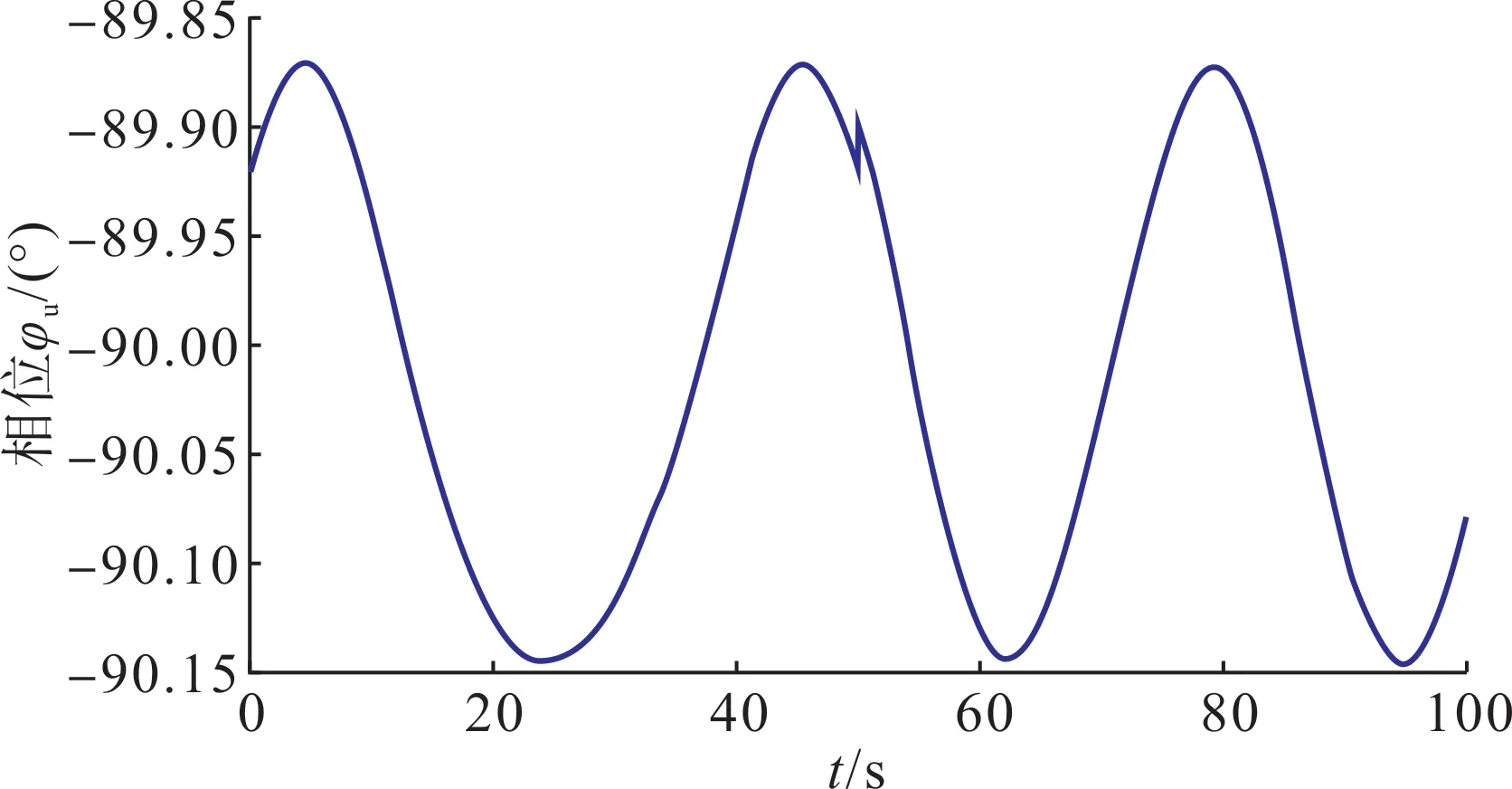
图21 待测电压相角测量值Fig.21 Measurement values of target voltage phase

实验结果表明，所提非接触式电压探头与电压测量方法能够实现绝缘导线的电压测量，幅值测量误差小于2%，相角测量误差小于0.2 °。

5 结论

本文提出了一种用于绝缘导线的非接触式电压测量方法。首先设计了基于电容耦合原理的多层薄膜柔性电压探头，采用金属薄膜和绝缘薄膜缠绕导线构建圆柱电容进行分压以获取待测信号。随后揭示了采样电路对探头分压情况存在不可忽略的影响，在此基础上提出了一种利用双探头差异输出逆向求解导线电压的方法。仿真和实验结果表明，所提非接触式电压测量方法能够在不破坏导线绝缘层的情况下测量电压的幅值、相角、频率等参数。在实验室条件下，对稳态工频电压的幅值测量误差绝对值小于2%，相角测量误差小于0.2 °。

当前所提非接触式电压测量技术仍处于实验室研究阶段，距离实际应用尚存在一定距离，现将待研究问题进行简要罗列供读者参考，包括但不限于以下内容。

1）含分布式电源的配电网中待测电压可能含有谐波、间谐波，不同频率成分经过电压探头后的增益与相移均不同，探头输出电压波形发生畸变，影响测量精度；

2）探头尺寸与便捷安装方式设计；

3）绝缘材料选取需要对材料的安全性、稳定性、探头制造成本等方面进行综合考虑，尽可能降低热胀冷缩、干裂、老化等问题对测量精度的影响；

4）电磁屏蔽问题需要利用屏蔽外壳防止空间电场窜入电压探头，提高测量精度；

5）电容值偏差引起的精度降低问题；

6）采样电路的量程与输入阻抗设计问题。