基于坐标映射及多重图划分的图相似查询研究
刘哲峰,梁 平,顾进广
(1.武汉科技大学 计算机科学与技术学院,湖北 武汉 430065;2.智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉 430065)
0 引 言
随着信息技术的迅速发展,所获得的数据呈爆炸式增加。根据国际数据公司(IDC)的统计,互联网上的数据每年将增长50%以上,而且世界上90%以上的数据是最近几年产生的[1]。这些数据中,容量巨大、结构复杂、种类繁多而且语义多变的数据占据了很大比例[2-3]。
总体而言,在数据及数据间的关系飞速增长的时代,图数据库被应用到越来越多的领域,如机电电力[4-5]、医学信息[6]、信用卡欺诈检测[7]等。而图形的激增也激发了人们对在大型图数据库中实现高效访问功能和灵活的结构感知查询的兴趣[8]。关于图数据库的查询方式,有检索条件约束[9]以及查询结果约束两大类,而基于查询结果约束,已经出现了许多相关的研究,它们可以大致分为两类:图精确搜索[10-11]和图相似性搜索[12-13]。与精确搜索相比,相似性搜索可以提供一种鲁棒的解决方案,允许容错并支持搜索未精确定义的模式。
两个标记图之间的相似性计算是图相似性搜索的核心操作,目前最主要的相似性度量为:图编辑距离[13-14]、最大公共子图[15-16]、图对齐[17]和图核函数[18-19]。该文考虑基于图编辑距离(GED)约束定义的相似性搜索问题,主要是因为其通用性和广泛的适用性[20],GED是一种几乎适用于任何类型的图形的度量。直观的图编辑操作可以精确捕捉与图形结构和内容相关的任何细粒度差异[21]。典型的编辑操作[22]是插入和删除顶点或边以及重新标记顶点或边。
该文研究了以下图相似性搜索问题:给定一个图数据库G={g1,g2,…,gn}和一个查询图q,需要找到图G中的所有图g,使其相对于查询图q的图编辑距离GED(g,q)在用户指定的阈值τ内。
然而,GED的计算是NP-hard,因此计算所有查询图q和g∈G的GED可能会导致较差的计算效率。现有的解决方案大多采用过滤验证框架来加快图形的相似性搜索。在过滤阶段,通过种种算法相对快速地评估出一个GED下界,它被用于从图数据库中修剪尽可能多的假阳性图,剩下的图构成候选集C。在验证阶段,必须在q和每个候选图之间执行GED计算来验证。
到目前为止,已经提出了不同的GED下界[13,21,23-24],这些技术具有一些缺点:(1)对于图数据库G中的所有数据图进行GED下界的评估,没有考虑到图规模的差距,会导致很多无意义的GED下界计算;(2)过于宽松的GED下界并没有保证其过滤能力,导致很多假阳性图无法识别;(3)GED下界评估耗时,会带来较高的验证成本。
该文考虑了一种基于坐标映射的多重图划分方法。首先,将图数据库以及查询图进行坐标系的映射,并以此为基础构建坐标系上的查询矩形对图数据库中不符合条件的图进行粗粒度过滤,以降低后续图划分的计算成本。这种过滤方式十分快速,但是并不精密;然后,使用基于参数的图划分的选择性计算方法有效地控制图划分的随机性,并基于该方法得到有效的GED下界,来提升过滤精度;最后,通过不同的划分方式以及参数控制构建不同的索引集,以实现多层索引过滤,更进一步提升过滤的精度。
1 问题定义
1.1 图与相似查询
该文采用的图均为简单的、无向的标记图。图g定义为一个四元组(Vg,Eg,lg,Σ),其中Vg是顶点集;Eg⊆Vg×Vg是边集;lg:Vg∪Eg→Σ是一个标签函数,其中Σ是顶点和边的标签集。
图g可以被执行的图编辑操作为:(1)删除一条边;(2)在两个顶点间插入一条边;(3)修改一条边的标签;(4)删除一个孤立的顶点;(5)插入一个孤立的顶点;(6)修改一个顶点的标签。
定义1(相似查询):给定一个图数据库G={g1,g2,…,gn},一个查询图q和一个GED阈值τ,相似查询的问题是找到一个数据图gi∈G,使得GED(gi,q)≤τ。
1.2 半边图与图划分
定义2(半边图):半边图g=(Vg,Eg,lg,Σ),其中,Eg⊆Vg×(Vg∪{*})是一个可能存在半边(u,*)∈Eg的图,其中一个关联顶点u∈Vg是一个确定的顶点,但该半边的另一个顶点(及其标号)没有明确的指定,表示为*。
定义3(图划分):图g可以划分为集合穷举、互斥和非空半边图的集合p,如下所示:
P(g)={pi|∪iVpi=Vg'∪iEpi⊆Eg∪Vg×{*},pi∩pj=∅,∀i,j≠j}
其中,P被称为g的一个划分。
将图划分为半边子图对GED有一个明显的优势,就是在给定任何图编辑操作的情况下,它最多只能影响一个半边图的划分。
2 基于坐标映射的多重图划分
2.1 坐标映射
在现实的图数据库中,图的规模均有较大的差异,而在图编辑操作中,对于顶点和边的删除或增加均是从图规模上进行操作。基于这一点,设计了一个坐标映射的批量过滤方法。
对于任一数据图g,将其以坐标(|Vg|,|Eg|),也就是基于顶点-边的方式,映射于二维坐标系中,其中,x坐标和y坐标分别代表图g的顶点数和边数。因此,对于图数据库G,可以获得点集{(|Vg|,|Eg|):g∈G},而这些点可以组成一个矩形区域A=[xmin,xmax]×[ymin,ymax],其中xmin/xmax和ymin/ymax分别是节点和边的最小数量和最大数量。
定义4(查询矩形):给定一个查询图q和阈值τ,查询矩形Aq被定义为由点集{(x,y):|x-|Vq‖+|y-|Eq‖≤τ}组成的矩形。
对于一个数据图g,如果GED(g,q)≤τ,那么必定会有:‖Vg|-|Vq‖+‖Eg|-|Eq‖≤τ。由此可以在矩形区域A中进行图规模上的批量过滤,圈定出如图1所示的查询矩形Aq。

图1 图数据库的坐标矩形A和查询矩形Aq
坐标映射的着眼点在于图的大小,考虑的是一种边界情况,这有助于从图规模上剔除了那些不符合要求的图,是一种粗粒度的过滤手段,以减少后续精细过滤的时间开销。因此,经过这坐标映射这一层的粗粒度过滤之后,所需要参与后续多重图划分的细粒度过滤的数据图数量明显减少,能显著加快后续细粒度过滤方法的索引构建时间。
算法1给出了坐标映射方法的算法描述。首先,初始化坐标矩形A的最大值和最小值(行1);然后,对于图数据库中的每个图,计算其顶点数和边数并更新A的最大值和最小值(行2~6),并将其坐标存储到坐标矩形A中(行7);接着,使用查询图的顶点数和边数计算查询矩形Aq,并找到与查询图相似的图的坐标(行9~11);最后,返回坐标矩形A和查询矩形Aq(行12)。
算法1:坐标映射方法
输入:图数据库G; 阈值τ;查询图q;
输出:坐标矩形A和查询矩形Aq
1→xmin=infinity,xmax=-infinity,ymin=infinity,ymax=-infinity;
2→for eachginGdo
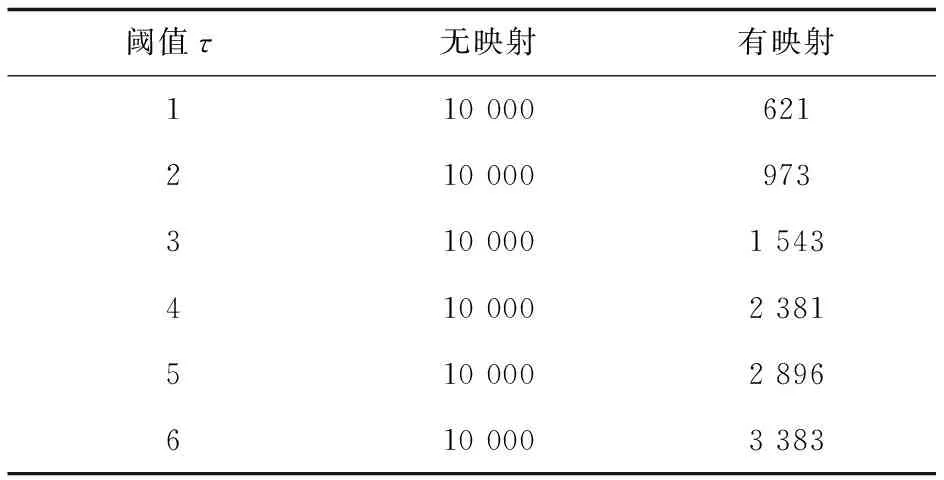
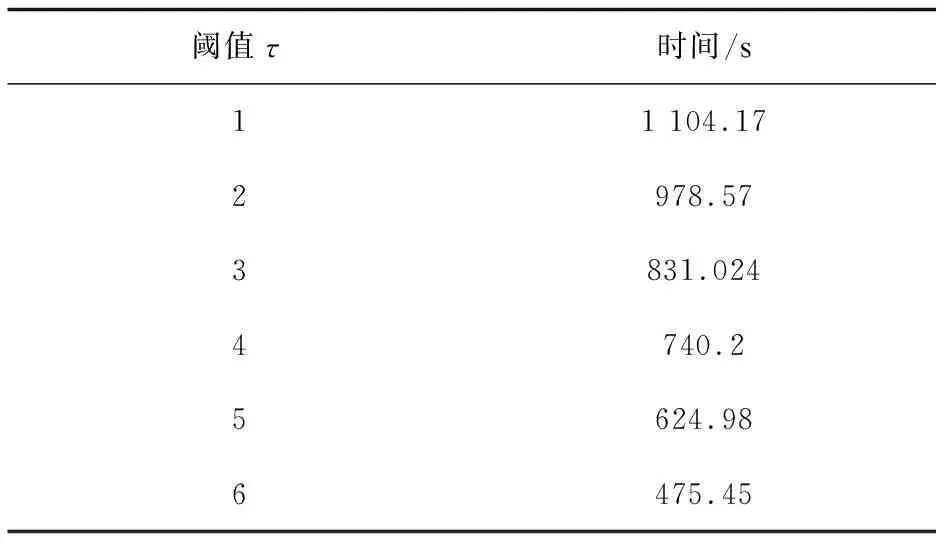
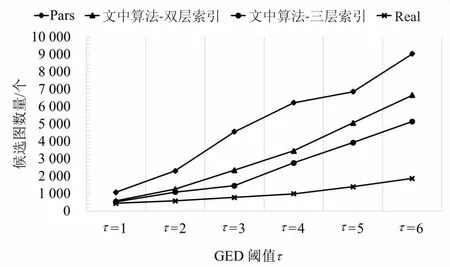
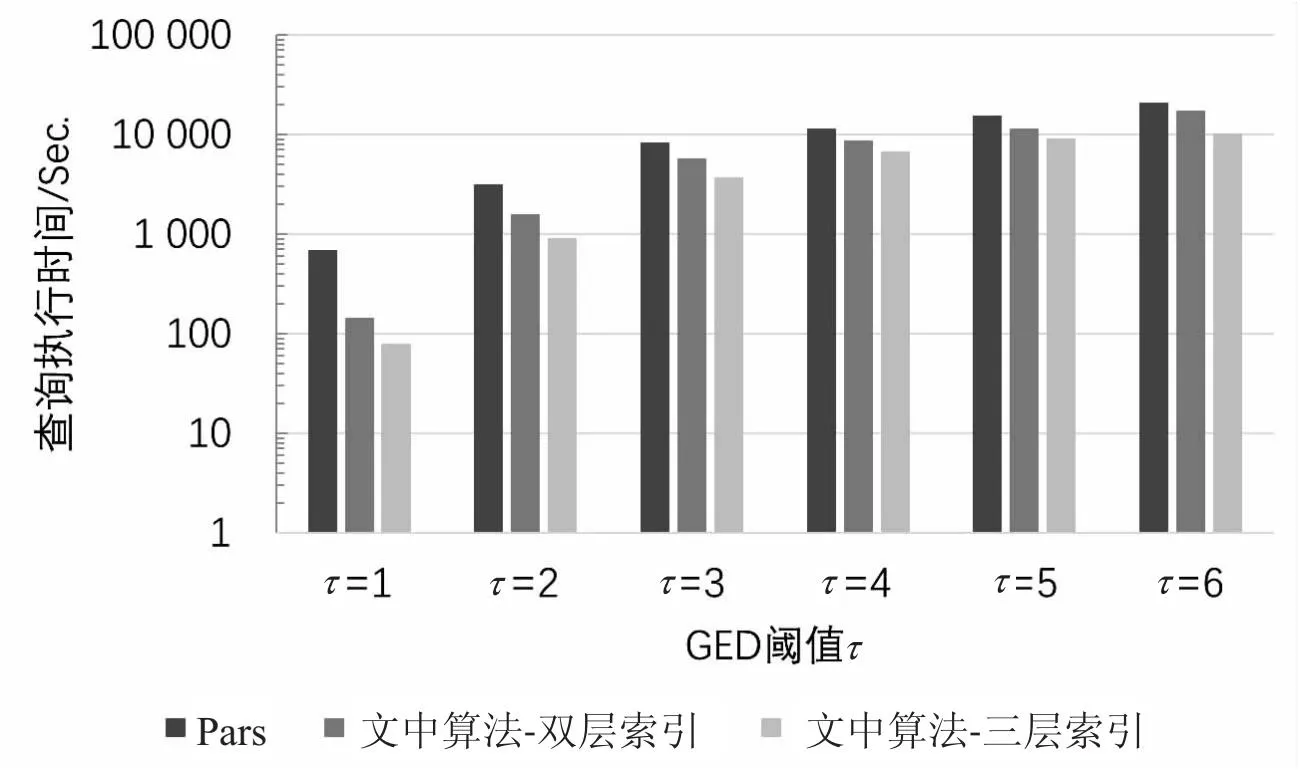
3→····if |Vg| 4→····if |Vg|>xmaxthenxmax=|Vg|; 5→····if |Eg| 6→····if |Eg| >ymaxthenymax=|Eg|; 7→····A.add((|Vg|, |Eg|)); 8→Aq= set(); 9→for eachginGdo 10→··if abs(|Vg|-|Vq|) + abs(|Eg|-|Eq|) ≤τthen 11→······Aq.add((|Vg|, |Eg|)) 12→returnA,Aq 由1.2中的定义3,可以推导出如下定理: 定理1:给定一个图g,该图被划分为(τ+k)个半边图,该半边图的集合为P(g),其中τ为阈值,k(k≥1)是一个整数参数。对于给定的查询图q,如果GED(g,q)≤τ,则在半边图集合P(g)中至少存在k个半边图:pi1,pi2,…,pik∈P(g),满足pil⊆q(1≤l≤k)。 对于任意数据图g∈G,其分区集合为P(g)={p1,p2,…,pτ+k},如果pi⊆q,则称pi为匹配分区,否则称其为不匹配分区。根据定理1,如果分区集合P中的匹配分区数小于k,则图编辑距离GED(g,q)必然是大于τ的,由此可判断出g是一个假阳性图,大大节约了时间成本。同时,为了更好地了解图划分方法的使用,给出了例子1进行说明。 例子1 对于图2中的数据图g1以及查询图q,假设阈值τ=2。令整数参数k=2,那么g1需要划分出四个半边图。对于图g1的划分P(g1)如图2所示。因为P(g1)相对于图q来说有三个不匹配分区:p1,p2和p4。因此g1是一个假阳性图。 图2 g1的四个半边图:P(g1)={p1,p2,p3,p4} 定理1提供了一个参数化的,基于分区的GED下界,通过设置不同的k值,就可以生成一系列新的GED下界。同时当k取不同的值时,新生成的GED下界的过滤能力也具有了一定的差异。当k=1时,实例化的GED下界归结为一个特殊的降级情况。对于给定的一个假阳性图g∈G,它的(τ+1)个分区,可以很容易地找到1个(k=1)匹配分区,一旦找到,g将被错误的纳入候选图中,然而当k>1时,g作为假阳性图将更有可能被识别和过滤,因为从g中检测k>1个匹配分区的可能性要远小于k=1时。 因此,k>1时,它比k=1这种退化情况更有可能识别出假阳性图。当k>1时,GED下界可以实例化为一系列更紧密的下界,对相似性搜索具有更好的过滤能力。 对于给定的任意一个数据图来说,可以有很多种划分方法,能将其划分为(τ+k)个不同大小和结构分区。因此如果不加以限制,图划分方法会充满随机性,针对这种情况同样给出了例子2进行说明。 例子2 同样是图2中的数据图g1,如果采用图3的划分方式,P1(g1)中,p2和p3均为匹配分区,此时数据图g1会通过筛选。 图3 g1的四个半边图:P1(g1)={p1,p2,p3,p4} 为了对这种随机划分方式进行限制,为每个分区赋予了一个如式1所示的选择性增益s(pi),它表明如果g是假阳性图,pi作为不匹配分区pi⊄q的选择性有多高,其中f()是图数据库G中的顶点/边的标签频率。为此,对于数据图的最优划分的目标是将数据图划分为具有最高总体选择值的(τ+k)个分区。 (1) 式中,s(pi)的值受两个因素的影响: (1)分区大小:较大的分区更有可能受图编辑距离的影响,从而使得该分区成为不匹配分区的概率更大; (2)顶点/边标签的频率:在查询图q中,标签频率在G中较小的分区可能按比例很少出现。因此,包含低频率顶点/边的分区更有可能是不匹配分区。 选择性划分的算法如算法2所示。对于输入的数据图g,首先创建一个布尔数组M,它表示是否将顶点v分配给某个分区,并将M初始化为false(行1);同时初始化另一个集合Una,它保存即将处理的数据图g的未分配顶点,初始化为空(行2);接下来选择τ+k个顶点,以此作为τ+k个分区的初始顶点,同时这些顶点的相邻且未被分配的顶点N(·)添加到Una中,这些存放在Una中的顶点将在下一步中考虑用于分区分配(行3~8);接着通过评估将每个顶点v分配给每个现有分区pi的选择性增益(由式1计算)来检查每个未分配的顶点,使得每个顶点分配到该分区后具有最大的选择性增益,并将顶点v的相邻且未被分配的顶点添加到Una中(行9~15);在所有顶点都分配完成后,就需要开始考虑跨区的边,并将它们作为半边分配给其中一个参与分区,同样需要计算所分配半边的选择性增益(行16~22)。这样通过贪心算法,将每一个除了初始化顶点以外的顶点和跨分区的边进行选择性增益的计算,最终返回相对最优的分区集合。 算法2:选择性图划分 输入:数据图g,阈值τ,参数k,查询图q 输出:图划分P(g)={p1,p2,…,pτ+k} 1→for eachv∈VgdoM[v]=false; 2→Una = ø*, /*Una为未分配顶点集合*/ 3→fori=1 toτ+kdo 4→····for onev∈VgandM[v]== false 5→········pi={v}; 6→········M[v]= true; 7→········for eachu∈N(v),M[u]==false andu∉ Una 8→············Una = Una∪{u}; 9→for eachv∈Una 10→··fori=1 toτ+kdo 11→······ei=s(pi∪{v})-s(pi); 13→··M[v]=true; 14→··for eachu∈N(v),M[u]==false andu∉ Una 15→······Una = Una∪{u}; 16→for each (u,v)∈Eg,uandv∈pi,i≠j 17→··ei=s(pi∪(u, *))-s(pi); 18→··ej=s(pi∪(v, *))-s(pi); 19→··ifei≥ejthen 20→······pi=pi∪{(u, *)}; 21→··else 22→······pi=pi∪{(v, *)}; 23→returnP(g)={p1,p2,…,pτ+k} 顶点和边标签的频率可以在构建坐标矩形阶段进行一次预计算,因此,该算法的时间复杂度为O((τ+k)|Vg|+|Eg|)。 上述的选择性图划分方式给原本的随机划分提供了一个约束,使得不稳定的随机划分变的更加可控。然而半边子图的匹配算法同样具有很高的代价,因此为了进一步降低半边子图匹配的验证成本,可以构建以下两个表进行进一步过滤: (1)标签频率表:为分区p构造一个标签频率表R(p),其中存储分区p的顶点和边标签的频率。在执行半边子图同构的计算之前,首先比较它们的频率表R(p)和R(q):对于R(p)中每个顶点/边标签的频率不应该超过R(q),记为R(p)≤R(q),这样可以节省半边子图同构的计算代价; (2)倒排索引:为图g的一个划分p构建一个倒排索引I(p)。对于给定的查询图q,如果p⊆q,可以在图数据库G中快速找到包含划分p的所有数据图。这样,在进行完必要的划分p的半边子图同构计算后,可以通过倒排索引找到所有包含划分p的数据图,以此减少大量的计算。 通过构建与维护上述两个表单,将子半边子图匹配的过程同样划分为过滤-验证两个部分,以进一步压缩计算成本。 虽然可以基于上诉方法选择一个紧凑的、基于划分的GED下界,并利用选择性划分的方法产生相对优秀的半边子图,然而可能仍然有一些假阳性图未被识别。因此选择采用多层索引结构来对图数据库进行过滤。 为了充分利用多个GED下界,采用集中过滤策略,考虑了L种不同的图划分方法,P1,P2,…,PL,其中Pi将g∈G划分为(τ+ki)个分区。具体来说,在第i层,评估由ki参数化的第i个GED下界,并生成候选图Ci,并由该候选图Ci继续进行下一层的过滤,当且仅当通过了所有层的GED下界评估之后,才能得到最终的候选集C。 为了保证索引分区和GED下界约束能在多层索引结构的不同层之间显著变化,考虑了以下策略: (1)在不同层应用选择性分区方法时,从数据图g中随机选择初始节点; (2)在不同层间选择不同的参数ki的值。 这样可以使用相同的选择性分区方法,通过不同的初始节点和不同的参数ki,保证每层索引都能产生不同的分区索引集,以此为GED下界提供严密性保证。 为了检测该算法的效率与准确性,将与Pars算法[23]进行对比实验。Pars算法是采用单个降级GED下界(k=1)和随机划分进行索引生成和相似性搜索的图索引方法,相较于其他的算法具有更好的效率,Pars算法所采用的半边子图同构算法与文中算法均为A*算法。同时为了体现坐标映射所带来的性能提升,将对文中算法以及Pars算法进行有无坐标映射的对比实验。 而对于文中算法,为了体现出在2.5节中提出的多层索引结构的过滤层数对算法的影响,实验中选取双层索引结构和三层索引结构进行对比。 随机从NCI/NIH数据集中选择10 000个图作为数据集,并从中随机选择一个图作为查询图。 在实验中主要考虑了以下性能评估指标: (1)索引构建成本:包括参与索引算法的图数量、索引构建时间; (2)候选图数量:即在进行过滤之后所产生的候选图数量; (3)查询执行时间:相似性搜索的真实响应时间,是候选集生成时间及GED验证时间之和,同样这里的时间是多次实验后平均的响应时间。 实验运行环境如下:Window11操作系统、16 GB内存的Core i7-11800H 2.30 GHz 8核电脑;Pars算法和文中算法均采用C++编程语言实现,编译环境为Microsoft Visual Studio 2022。 3.2.1 索引构建成本 首先,在图数据库中评估不同方法的索引构建成本。值得注意的是,图索引是离线预构建的,对于图数据库G,考虑GED阈值τ是很小的(τ≤4),其主要原因是用户会更倾向于从图数据库中搜索相似的图。 表1为在不同阈值τ下,无坐标映射和有坐标映射时,参与索引构建的数据图数量。从表1可知,有坐标映射时,会过滤掉相当一大批从图的规模上就不符合要求的数据图,从而大大减轻了索引的构建负担。同样,当阈值越大时,说明用户对相似度的要求越松,通过坐标映射的数据图数量也会大幅度上升,但是哪怕阈值τ已经为6了,它仍然能过滤掉近2/3的数据图。 表1 有无坐标映射时参与索引构建的图数量 图4表示在无坐标映射时Pars算法、采用双层索引及采用三层索引的文中算法的时间开销。可以看到可以有效构建多层索引。同样,因为需要构建多层索引,以及需要选择较好的图划分,多层索引在构建时间上略长于Pars算法的单层随机划分的索引。而随着阈值τ的增加,这种索引构建时间的差距开始变的微不足道,这是因为当τ变得更大时,每个数据图会相应地被划分为更大数量的更小分区,从而导致半边子图同构计算加速,而半边子图同构的计算时间通常会占用总索引构建时间的90%以上。 图4 无坐标映射的索引构建时间 表2给出了在AIDS中不同阈值、无标签频率表及倒排索引表的情况下,半边子图同构所需要的时间。之所以排除标签频率表和倒排索引表的干扰,是因为这两者很大程度上会受到图划分的影响,若是采用随机划分方法,那么在不排除标签频率表和倒排索引表的情况下,半边子图同构时间会变的相对随机,若是采用文中的选择性划分方法,那么半边子图同构时间的影响因子又会变的过多。从表2可以看出,随着阈值的增大,半边子图同构的时间会被加速。 表2 半边子图同构时间 图5表示在有坐标映射时,Pars算法、采用双层索引和采用三层索引的文中算法的索引构建时间对比。从图5可知,其与图4变化趋势不同:随着阈值τ增大,索引构建的时间整体呈上升趋势。结合表1可以发现,当阈值τ增大时,表明对查询图的相似性要求越来越低,通过坐标映射的图的数量显然会越来越多,这就导致了参与索引构建的图的数量上升,因此在阈值变大的情况下,哪怕有着半边子图同构的计算加速,参与计算的图数量显然影响更大。 图5 有坐标映射的索引构建时间 3.2.2 候选图数量 其次,比较了不同方法所产生的候选图数量。图6表示Pars算法、采用双层索引及采用三层索引的文中算法所产生的候选图数量,其中Real表示实际的相似图数量。从图中可以看出,文中所采用的算法,其过滤出的候选图始终小于Pars,哪怕是双层索引结构都能比Pars算法减少近45%的假阳性图。原因有两个:首先,参数k>1的广义GED下界比降级(k=1)的更紧密;其次,选择性分区方法比Pars中的随机分区更有效地生成高选择性的索引分区,这有助于更进一步地过滤假阳性图。另外,可以看到当索引层数增多,被过滤掉的假阳性图也显著增加,这表明多层索引方法具有更出色的过滤能力,与Pars的单层随机划分的方法相比,可以保证假阳性图数量的减少。 图6 候选图数量 3.2.3 查询执行时间 最后,评估了Pars算法、采用双层索引及采用三层索引的文中算法的总体运行的时间成本。因为评估的是最终的候选图及GED验证的时间,故而有无坐标映射对该部分几乎是没有影响的。评估结果如图7所示。可以发现,相比于随机划分的单层过滤方法Pars,文中的多层索引的过滤效果要更好,因为坐标轴是按指数增加的,所以就算看起来没有增加多少,但实际上是差距越来越大的,这主要是因为多层索引所生成的候选集明显更少,这样总体运行时间才会更少,说明选择性图划分方法的多层索引结构明显具有更好的,更精确的过滤效果。 图7 查询执行时间 综合上述的实验结果可以得出以下结论:首先,基于坐标映射的预过滤方法可以有效减少参与后续细粒度过滤方法的数据图数量,从而明显减少细粒度过滤方法的索引构建时间;其次,虽然在索引构建阶段,文中算法因为需要对分区质量进行调整,所以整体索引构建时间要略长于随机划分的Pars算法,但是图6和图7的实验结果表明,其过滤性能与精度是要明显优于Pars算法的,从整体的查询速度来看,文中算法的整体查询速度是要明显优于Pars算法的。 相似性搜索问题在管理和查询图结构数据中起着最基本的和最关键的作用,并且在现实世界中大规模的图数据库中有广泛的应用。该文探讨了在图编辑距离的约束下的相似性搜索问题,并在Pars算法的基础上进一步引入多层索引结构来解决图相似性搜索这一问题,同时针对多层索引结构的构建时间开销过大的问题,提出了坐标映射的批量图处理方式来有效减少过滤阶段的时间成本。首先采用坐标映射来过滤掉一大批从规模上就超出相似度阈值的图,然后使用参数化的、选择性图划分方式的GED下界来过滤假阳性图,以此使得图划分变得更加可控,同时通过倒排索引和标签频率表来减少子图同构的时间开销,最终通过生成多个索引集来对批量过滤后的图再次进行交叉检查,以此提升过滤的精度。这样,在保证多层索引过滤精度的同时,使用坐标映射大大减少了时间成本。模拟实验结果证明,坐标映射提升了算法的时间性能,而多层索引的引入提升了算法过滤的精度。2.2 参数化的GED下界

2.3 选择性图划分

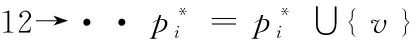
2.4 标签频率表与倒排索引
2.5 多层索引
3 实验结果及分析
3.1 实验环境
3.2 实验结果分析


4 结束语

