基于群稀疏正则化的高光谱图像去噪

姜 斌,叶 军

(南京邮电大学 理学院,江苏 南京 210023)

0 引 言

高光谱图像(hyperspectral image,HSI)在遥感通信领域占有重要的地位,包含数十至数百个对目标区域连续的窄波段成像结果[1]。因含有丰富的光谱信息和全面的空间信息,HSI在食品安全、质量控制、工业等领域有着十分广泛的应用[2]。但图像在采集过程中会受到各类噪声的污染,如高斯、椒盐、条纹噪声等,使得图像质量严重退化[3]。被混合噪声污染的HSI视觉效果下降,将丢失大量有用的信息,对后续应用造成非常严重的影响,因此对HSI进行去噪算法的研究是后续步骤实施的前提[4]。

迄今为止,许多不同的去噪方法被提出用于恢复高光谱图像。传统方法是将HSI看作许多二维灰度图像的叠加,对每个波段的图像单独去噪,代表方法有块匹配三维滤波算法[5]、K-SVD算法[6]等,然而这些方法忽略了不同光谱波段之间的强相关性,容易造成HSI中的光谱特征失真。此外,将HSI空间低秩性和光谱低秩性相结合的方法也取得了显著的发展。低秩矩阵恢复方法(low-rank matrix recovery,LRMR)[7]将张量结构的HSI数据沿光谱维转化为Casorati矩阵,再对其施加低秩约束进行去噪。但是LRMR方法忽略了条纹噪声的低秩结构,对于条纹噪声去除效果不佳,因此有必要在HSI的去噪过程中单独考虑条纹的独特低秩性质。

除了全局低秩性外,局部平滑性是HSI的另一个重要性质。全变分(total variation,TV)[8]作为平滑保留的一种有效方法,通过最小化相邻像素之间的差值来实现图像去噪,如全变分正则化低秩矩阵分解方法(total-variation-regularized low-rank matrix factorization,LRTV)[9]、增强型三维全变分正则化方法(enhanced 3D total variation,E3DTV)[10]。虽然这两种基于TV的方法能够保持图像边缘信息,但是在去除强烈混合噪声时图像空谱维的平滑性降低。针对此缺陷,文献[11]在低秩张量分解的框架下分别探索HSI空间因子的群稀疏性和光谱因子的连续性,提高了HSI的整体平滑性。然而,上述方法仅针对空间维的群稀疏性进行恢复,没有利用光谱维的平滑性。

为了充分利用HSI的内在先验信息并减少混合噪声产生的影响,提出新的基于群稀疏正则化的高光谱图像去噪算法。一方面,针对条纹噪声的独特低秩性质将其单独建模,提升结构化条纹噪声的去除效果。另一方面,采用一种新的群稀疏正则化约束HSI的空间-光谱平滑性,有效保持了图像的边缘信息。该文的贡献如下:

(1)综合考虑干净HSI和各波段上条纹噪声的低秩特性,利用HSI每个波段上条纹的低秩结构对条纹单独建模,解决了条纹难以与干净图像分离的问题。

(2)构造一种新的群稀疏正则化,即基于L2,1范数的E3DTV正则化,该正则化不仅能够有效地去除混合噪声,还提高了空谱维的平滑性。

(3)采用交替方向乘子法求解所提出的模型,推导了交替迭代规则,形成了相应的算法。大量实验结果表明,提出的算法在结构化混合噪声去除、图像平滑性恢复方面都有优秀表现。

1 高光谱模型

1.1 扩展的高光谱退化模型

HSI在成像过程中会受到高斯噪声、脉冲噪声、死线、条纹噪声等多种类型噪声的污染,现有的去噪方法[7-10]将矩阵形式的HSI退化模型表示为:

Y=X+S+G

(1)

其中,Y为受噪声污染的高光谱图像,X为干净图像,S表示稀疏噪声,G表示高斯噪声。它们都是大小为mn×p的Casorati矩阵(对所有HSI数据列按字典顺序重新排列的矩阵),m和n分别表示高光谱图像的宽和高,p表示波段数。

式1假设条纹噪声仅占图像的一小部分而将其归属为稀疏噪声,然而在复杂的混合噪声场景下,特别是当出现高强度结构化条纹噪声时,往往无法有效地去噪和去条纹,甚至会造成空间和光谱的畸变[12]。因此,考虑到条纹噪声的产生和分布不同于其他类型的稀疏噪声,在式1的HSI恢复框架中对条纹噪声单独建模以利用其独特的先验信息,将式1扩展为:

Y=X+S+G+B

(2)

其中,B表示条纹噪声,大小为mn×p。去噪目标是从受损的Y中恢复干净的X,优化模型表示为:

(3)

其中,τ,β,λ是正则项参数。

1.2 群稀疏正则化

对于干净的HSI矩阵X∈Rmn×p,其沿光谱维聚合为立方体X∈Rm×n×p,满足X=unflod(X)和X=flod(X),E3DTV范数定义为:

(4)

式中,∇表示矩阵上的特殊差分算子,即:

∇jX=unfold(Dj(X)),∀j=1,2,3

(5)

其中,D1,D2,D3可定义为:

(6)

E3DTV模型虽然可以保留图像边缘信息,但面对强噪声干扰时会将结构化噪声视为边缘结构而保留,图像空谱维的平滑性明显下降。因此,考虑到高光谱图像在不同波段上的稀疏性是独立且不均匀的,通过探索其差分图像低秩子空间的群稀疏先验信息来进一步加强图像空谱维的平滑性,该文提出一种新的群稀疏正则化,该正则化能够较好地利用空谱维的内部联系性,提升混合噪声的去除效果以及保证空谱维的平滑性。对于干净图像X,群稀疏正则化表述为:

Uj∈Rmn×r,Vj∈Rp×r,j=1,2,3

(7)

1.3 基于群稀疏正则化的HSI去噪模型

将群稀疏正则化(式7)融入到扩展的HSI去噪模型(式3)中,即:

rank(X)≤r,rank(Bi)≤rB

(8)

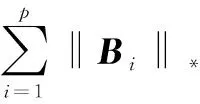
2 基于交替方向乘子法的算法求解

采用交替方向乘子法(ADMM)[13]求解所提出的HSI去噪和去条纹模型,首先将式8转化为Lagrange函数:

L(X,S,B,Uj,Vj,Nj,Λ)=

(9)

式中,Λ和Nj(j=1,2,3)是拉格朗日乘子,μ是惩罚参数。对Lagrange函数中的某一变量迭代优化而其余变量单步固定的方法对式9进行求解。在第k+1次迭代中,按如下方式更新变量:

(1)更新变量X。

X(k+1)的解可以通过式10获得:

(10)

X(k+1)=

(11)

(2)更新变量Uj,Vj(j=1,2,3)。

(12)

式12可以使用shrink算子[11]来求解,即:

(13)

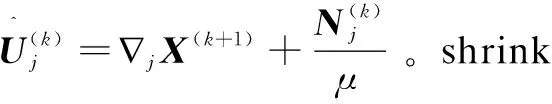
(14)

(15)

式15的解由以下定理获得:

因此Vj的更新方程为:

(16)

(3)更新变量B,S和拉格朗日乘子。

首先,将包含变量B的子问题表示为:

(17)

考虑到各波段条纹噪声都具有特殊的低秩结构[12],因此对条纹噪声逐波段优化处理,将式17表示为:

(18)

其中,Yi,Xi,Si,Λi表示第i波段的矩阵。式18的解由以下定理获得:

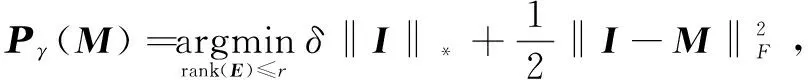
(19)

其次,将包含变量S的子问题表示为:

(20)

式19可以使用软阈值收缩算子[17]来求解:

(21)

软阈值收缩算子的具体定义如下:

(22)

最后,更新拉格朗日乘子:

(23)

算法1:高光谱图像去噪算法

输入:含噪高光谱图像Y,秩r和rB,最大迭代步数kmax,迭代停止条件ε,正则项参数τ,β和λ

初始化:X=S=B=0,Λ=0,N1=N2=N3=0,ρ=1.2,μ=0.05,μmax=106

令k=k+1,迭代下列步骤:

(1)根据式11,更新X

(2)根据式13和式15,更新Uj,Vj(j=1,2,3)

(3)根据式19,更新B

(4)根据式21,更新S

(5)根据式23,更新拉格朗日乘子

(6)更新惩罚因子:μ=min(ρμ,μmax)

输出:干净的HSIX

3 实验与分析

3.1 对比算法

在对比实验上,选取5种主流的HSI去噪算法进行比较,即LRMR方法[7]、LRTV方法[9]、3DLogTNN方法[18]、E3DTV方法[10]和LRTFDFR方法[11]。其中,LRMR方法将三维HSI立方体分割成多个小块,采用RPCA算法进行去噪;LRTV方法将核范数、TV正则化和L1范数集成为统一的框架,分别探索光谱低秩特性和空间分段平滑性;3DLogTNN方法采用log簇函数近似表示张量的纤维秩,以实现更准确的HSI秩表征;E3DTV方法将稀疏性用于沿所有波段的子空间基映射来反映HSI差分图像的稀疏性;LRTFDFR方法在低秩张量分解的框架中分别探索空间维的群稀疏性和光谱维的连续性,通过增强光谱维的连续性来促进HSI整体的平滑性。

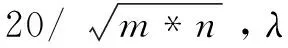
3.2 评价指标

采用峰值信噪比(PSNR)、结构相似性(SSIM)、平均光谱角距离(MSA)和相对无量纲全局误差(ERGAS)(详见文献[10,12])进行定量评估。MPSNR和MSSIM是所有波段图片的PSNR和SSIM求和平均值,其定义如下:

(24)

(25)

(26)

(27)

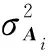
3.3 仿真数据实验

选取Indian pines数据集[19]作为仿真实验对象,它包含空间尺寸为145×145的图片224张。在去噪前,将HSI的灰度值逐波段归一化为[0,1]。

由于HSI中的噪声通常表现为实际噪声场景中几种噪声的混合,在Indian pines数据集上模拟添加高斯噪声、脉冲噪声、死线和条纹:

Case1(高斯+脉冲+死线+周期性条纹):在所有波段添加方差为0.05的高斯噪声和百分比为0.05的脉冲噪声;在第51～54波段添加死线,死线的数量随机选取为1～3;同时,选取50个波段加入条纹噪声,且条纹的数量为图像宽度的20%,均匀分布在所选波段上以呈现其周期性。

Case2(高斯+脉冲+死线+随机性条纹):在所有波段加入方差为0～0.2的高斯噪声和百分比为0%～20%的脉冲噪声;随机选取40个波段添加死线,死线的数量随机选取为1～3;同时,在第111～180波段的同一位置添加条纹,且条纹的数量为图像宽度的30%,随机分布在所选波段上以呈现其随机性。

文中方法和5种主流方法的4个评价指标情况如表1所示。每个评价指标的最优值用粗体标出,次优结果用下划线标注。可以看出,文中方法的4个主要指标在不同加噪情况下都优于对比方法的。

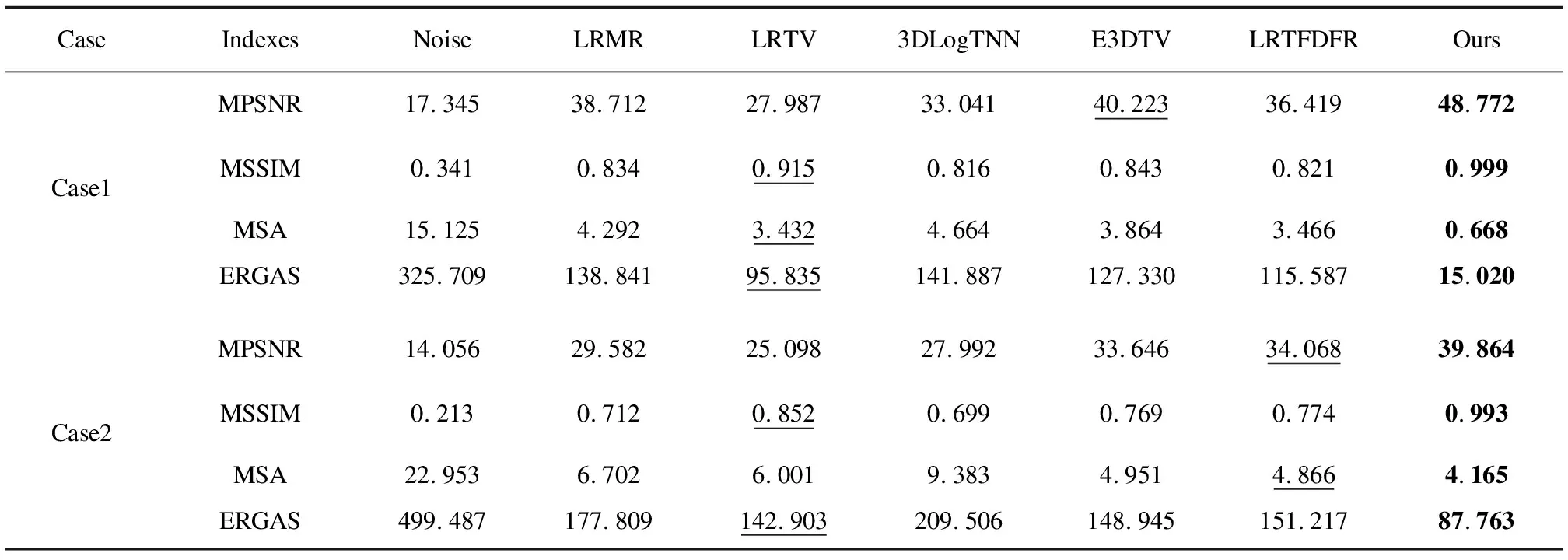
表1 不同方法恢复结果指标MPSNR,MSSIM,MSA和ERGAS

图1展示了在受噪声污染较严重的Case2情况下第124波段去噪结果。5种对比方法在结构化条纹噪声去除以及图像细节还原上有明显不足,恢复结果包含大量结构化条纹噪声残留,文中方法则能够对混合噪声进行有效处理,很好地保留了图像的全局结构和边缘信息。

图1 Case2第124波段实验数据对比

3.4 真实数据实验

选取Urban图像[19]作为真实数据集,该数据集大小为200×200×210,其中很多波段被死线和条纹噪声严重破坏。图2给出了Urban数据集第139波段的去噪结果,可以看出LRMR,LRTV和3DLogTNN对于条纹的去除效果不佳;E3DTV存在条纹去除不完全的问题;LRTFDFR和文中方法则成功地去除了图像中的混合噪声,并且完整地保留了图像细节。

图2 真实数据集Urban第139波段去噪效果对比

3.5 收敛性和参数分析

针对所提方法的收敛性,采取实验的方式对Indian Case2进行分析。图3给出了在Indian Case2下MPSNR和MSSIM随迭代次数的增加而变化的情况。随着迭代次数的增加,两个量化指标MPSNR以及MSSIM的提升十分明显,并且在迭代30步后该数值变化逐渐趋于稳定,表明文中方法具有良好的收敛性。

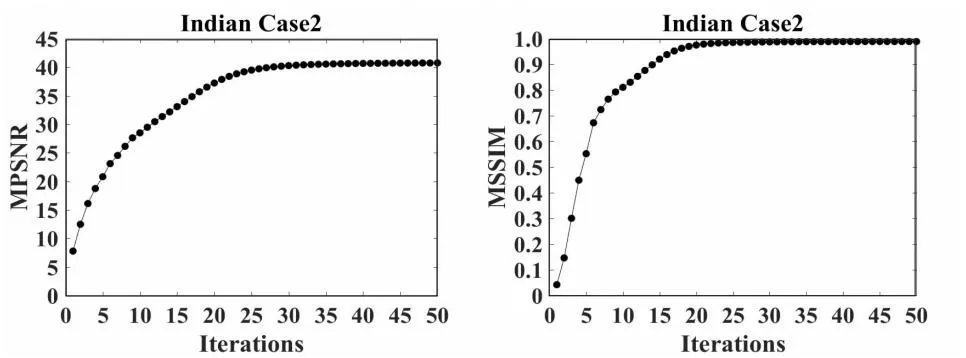
图3 MPSNR和MSSIM随迭代次数的变化情况

图4 MPSNR和MSSIM随参数τ,β的变化情况

4 结束语

该文提出一种基于群稀疏正则化的高光谱图像去噪算法,充分利用了高光谱图像的内在低秩结构以及空谱维内在关联性。通过扩展HSI去噪模型,解决了结构化条纹噪声难以去除的问题,对于高光谱图像恢复效果明显。同时,通过利用HSI内部的群稀疏性,很好地保留了图像的边缘和纹理信息。仿真和真实的数据实验表明,所提出的模型在应用中有更好的鲁棒性,并在评价指标和去噪目视效果上,该方法明显优于现有的主流方法。同时,针对HSI空间-光谱独特结构进行合理有效的建模,以进一步提升去噪效果,将是未来的研究重点。