现代智慧教育下的认知诊断模型比较分析研究

丁泽元,梁嘉辉,张云飞,郝 飞,李 鹏,郭龙江

(陕西师范大学 计算机科学学院,陕西 西安 710119)

0 引 言

认知诊断是指对个体知识结构、加工技能或认知过程的诊断评估[1],主要应用在游戏、教育、医疗诊断等领域,其中在智慧教育领域应用最为广泛[2]。认知诊断对传统考试的测验与评价体系进行了改进,它旨在探究学生在学习过程中的状态。通过分析学生的答题记录和试卷信息,推断出学生当前的知识状态,进一步得到学生对知识点的熟练程度,进而全方位地对被测者认知的长处与不足进行评估和诊断,以达到具有针对性地促进被测者全面发展的目的。

具体过程如图1所示。

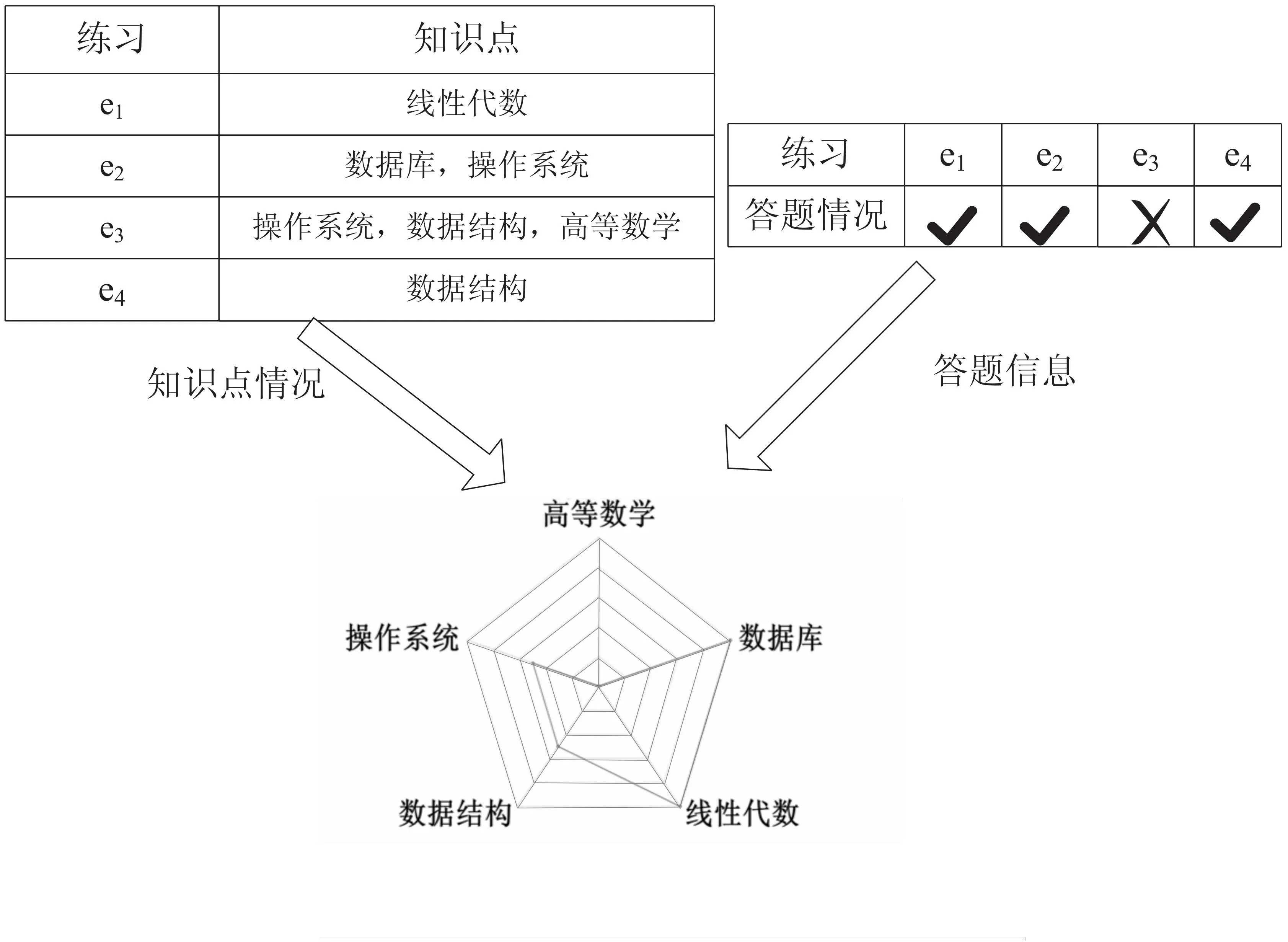
图1 认知诊断过程

学生选择一组练习(例如,e1,…,e4),之后写下他们的答案(例如,对或错)。然后,根据相应的概念(例如线性代数)来推断他们的实际知识状态以及掌握程度。可以看到,e1-e4每个题目都对应知识点相关内容,可以看到这个同学e1题目作对了,那么在诊断报告中会认为这位同学对于e1所考察的线性代数的掌握度比较高,若e3题目做错了,那么就会得出学生对操作系统、数据结构和高等数学掌握的不够好。

该文从ASSISTments 2009-2010 Skill-builder data数据集获得了346 860条样本,首先进行数据预处理;其次通过特征选择选出有助于认知诊断任务的特征;由于IRT和DINA模型分别是最为典型的连续型和离散型认知诊断模型,因此二者能较好表征出传统认知诊断模型的特点。MIRT是IRT模型最具代表性的变体,体现了认知诊断由仅关注学生的单一维度的能力到聚焦学生多维能力的视野变化,是认知诊断领域发展的一个重要里程。而NeuralCD模型是认知诊断领域最新的产物,它以人工神经网络为基础,体现了认知诊断领域与深度学习领域的进一步紧密结合,是认知诊断领域发展的又一重要里程。因此,该文选用了这4个模型,以Precision,Recall,F1_score和Accuracy作为模型认知准确度的误差分析指标,并比较了不同模型的可解释性。最后,分析了比较结果并总结了不同模型在现代智慧教育中的适用场景,为认知诊断研究提供了新视角。

1 背景信息

1.1 历史发展

17世纪,真分数理论开始萌芽,这也是经典测量理论(CTT)的前身[3]。1904年,C.Spearman提出对于测量误差引起的衰减的相关系数的校正思路[3],正式标志着经典测量理论的诞生。迄今为止,经典测量理论仍是最为广泛的一种测量理论。

1972年,Cronbach提出了概化理论(GT)[3]。它综合使用方差分析模型等统计方法在一定范围内对误差进行控制,提高了测量的可信度。相比CTT,GT可以更加有效地去提升测量精度与准确性。

1951年,F.Lord发表的博士论文《A Theory of Test Scores》标志着IRT理论的诞生[3]。同时期,丹麦数学家G. Rasch提出了IRT的函数形式和单参数模型。而在随后的30年中,F.Lord依次提出IRT的双参数模型和三参数模型[3],并最终于1980年出版了《Applications of Item Response Theory to Practical Testing Problems》,完善了整个IRT理论的框架,使得IRT理论与CTT,GT并列为教育测量领域最为重要的三大理论。

随着现代教育技术水平的精进,Frederiksen等人于1993年在《Test Theory for a New Generation of Tests》中提出了新一代测量理论的概念,并将CTT,GT和IRT都归为标准测量理论的范畴[4-5]。书中指出标准测量理论只会给被测者一个整体的能力水平测量及评估,缺乏对被试者心理认知能力的研究。而新一代测量理论同时兼具整体诊断和细节分析、囊括能力水平测量和认知水平评估。时至今日,新一代测量理论已然演变为认知诊断。

1.2 研究现状

现有的认知诊断研究主要分为三大类:基于传统的认知诊断角度、基于数据挖掘角度以及基于人工神经网络。

基于传统的认知诊断角度的模型的主要特点是将学生回答练习的结果建模为学生的特质特征和练习之间的交互作用。此类模型由原始的IRT模型和DINA模型,衍生出了MIRT等一系列新模型。其中,IRT属于能力水平研究范式,强调整体的能力水平测量及评估;而DINA和MIRT属于认知水平研究范式,强调理解个体心理层面的认知加工过程和对被试的认知状态做出详细分析。

近年来,一些基于数据挖掘角度的认知诊断方法发现了矩阵分解在认知诊断中的可行性与适用性。学生在矩阵分解中被认为是用户,而习题对应于矩阵分解中的项目。如Thai-Nghe等人[6]在教育背景下应用了矩阵分解等技术实现了推荐系统,并与传统的回归方法进行了比较。Thai-Nghe等人[7]提出了一种多关系因子分解方法用于智能辅导系统中学生建模。Liu等人[8]为平衡模型的认知准确度和可解释性,以矩阵分解为基础提出了同时考虑主观和客观测验类型的FuzzyCDF。然而矩阵分解获得的潜在特质向量中的元素与特定知识概念之间没有明确的对应关系,因此并不能推断出学生对于知识点的掌握情况等信息。

基于人工神经网络的认知诊断技术主要有深度知识追踪(DKT)以及神经认知诊断等模型。深度知识追踪[9]对学生的学习过程进行建模,继而跟踪学生知识状态的动态变化。然而,DKT更多的是预测下一时刻学生答对各道题目的概率,并不区分试题本身与其蕴含知识点,因此DKT并不适合直接用作认知诊断方法。而对于NeuralCD这一模型在后续的2.4节中会详细介绍。

2 典型认知诊断模型

2.1 项目反应理论

项目反应理论是用来分析考试成绩的标准测量检验模型。IRT基于3个基本假设建立了项目性能、被试潜在特质水平与项目应答正确概率之间的关系[10]。相比CTT,IRT是非线性的概率模型,因此它对被试者的分析、对测试项目的分析更加细致与具体,常被视为CTT的升级。

IRT的3个假设如下:

单维性假设:假设某个试题只测量学生的某一种能力。

独立性假设:假设学生在每一个试题上的作答反应是相互独立的,且作答反应只与学生自身的能力水平有关,与其他因素无关。

模型假设:学生在测验上的正确作答概率与被试的能力水平可以通过函数关系反应。

IRT的核心公式是:

(1)

此公式代表的含义是在当前的学生能力参数、试题区分度以及试题难度的情况下,学生做对该题的概率。其中,Xji代表第j位学生做对第i道题的概率;θj代表第j位学生的能力参数;αi代表第i道题的区分度;βi代表第i道题的试题难度。

2.2 多维项目反应理论

随着IRT模型较多地用于实践,大家逐渐认识到IRT模型的单维性假设不符合现实场景:人们在完成某项测验任务时需要多种能力去协调配合是吻合的,极少有测验它只评定人们单维度的能力[11]。

因此,人们基于项目反应理论和因素分析理论发展出了多维项目反应理论。由于其兼备了项目反应理论和因素分析的优点,多维项目反应理论和认知诊断、计算机化自适应测量共同被看作是当代心理测量理论的3个重要的发展方向[12]。

实用性最好的Logistics多维项目反应模型的项目反应函数表达式为[13]:

(2)

其中,θi=(θi1,θi2,…,θik)表示学生i的第k维能力的向量;αj=(αj1,αj2,…,αjk)表示试题j在第k维的区分度的向量;dj表示和MIRT难易程度相关的参数,它虽和IRT模型的难度参数不同,但二者可以相互转换;cj表示为试题猜测度参数。

2.3 DINA模型

DINA模型是一种典型的离散型认知诊断模型[14]。该模型结合Q矩阵,将学生看作一个多维的知识点掌握向量。DINA模型简单,易于识别,且具有很好的模型拟合度,因此具有较好的发展趋势[15]。

DINA模型也是一种潜在性分类模型,适合用于二值记分的项目评测,从而实现认知诊断[15]。该模型可以诊断被试者的认知属性掌握的概率,相比其他复杂的、多参数的模型,DINA模型仅有两项参数,即“失误”和“猜测”。两项参数所对应的数学符号为sj(学生熟练掌握了试题j所考知识点的情况下丢分的概率)和gj(学生在未掌握试题j所考知识点下得分的概率)。在已知学生i的知识点掌握情况的前提下,试题j成功答对的概率表达式如下所示:

(3)

其中,Yij表示学生i对试题j的作答情况;αi=(αi1,αi2,…,αik)表示学生i的知识状态,k代表试题j所考察的知识点个数;Pj(αi)为学生i在知识状态为αi的情况下正确作答试题j的概率;ηij代表学生i在试题j上面的潜在的作答情况[15]。

2.4 神经认知诊断模型

传统的认知诊断不能具体清晰地捕捉学生与试题之间复杂的关系,比如IRT模型只能给出学生单一的能力值、DINA模型对知识点掌握程度的评价只有掌握和没掌握[16]。

而神经认知诊断框架,通过将神经网络用于比较复杂的非线性交互建模,避免了依赖人工定义的函数[2]的弊端。该文使用的NeuralCD模型通过将学生和试题投影到因子向量,使用多层建模去模拟学生回答试题这一复杂的交互,为了保证该神经网络有良好可解释性,引入教育理论中的单调性假设,从传统的Q矩阵中去提取试题的因子向量,并通过使用全连接层去保证单调性。

认知诊断模型,通常需要考虑的因素有3个:学生、试题以及学生和试题之间的相互作用。NeuralCD框架的结构如图2所示[1]。

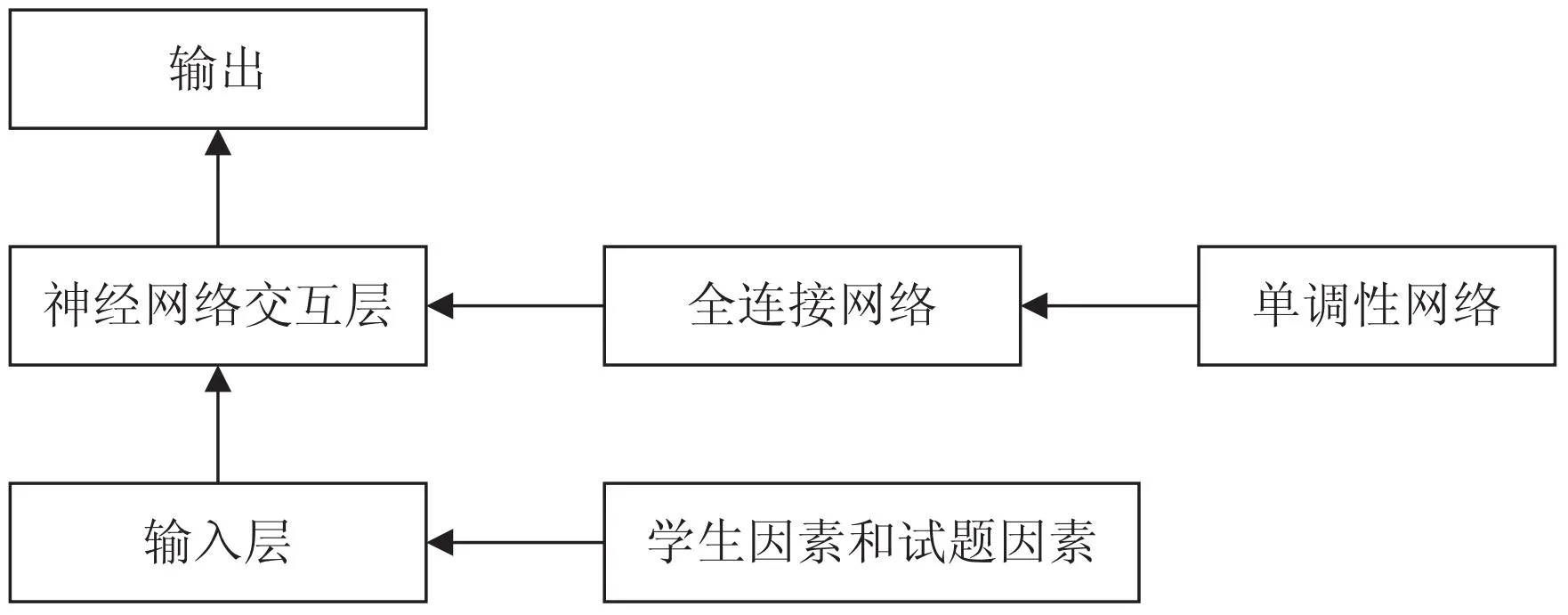
图2 神经认知诊断框架

对于学生的每一条做题记录,使用对应学生和试题的独热编码作为输入。学生和试题的诊断因子被输入进交互层。在框架的全连接层,假设在学生知识水平的任何维度上,正确回答练习的概率都是单调递增(即掌握知识越多,答对概率越高)的单调性假设来保证框架的可解释性。该框架的输出为学生个体正确回答具体一道试题的概率.

(1)学生因素。

学生因素即每一位学生对每一个知识点的熟练程度(即掌握情况,不采用0/1值,而采用0-1之间的连续值),采用DINA模型中使用的方法,将[0,1]二值变为连续值[2]。

使用Fs向量来描述学生个体,Fs为知识熟练度向量,其中每一个元素都是连续的,表示具体学生对具体一个知识点的掌握程度。

(2)试题因素。

试题因素就是试题与知识点之间的关系和其他因素这两类。试题和知识点之间的关系是考虑的最基本的因素,其每个元素对应着所诊断的目标的具体的知识点,即知识相关向量,用Fkn表示,它的维度和Fs是一样的,表示试题与知识点之间的相关性。其他因素可以使用IRT模型和DINA模型中采用的因素,比如知识难度、试题难度和试题的区分度等。

(3)交互函数。

该文是通过人工神经网络来获得交互作用函数的,让神经网络从数据中去学习。神经网络可以逼近任何连续函数并且其强大的拟合能力是可以捕捉到学生与试题因素之间的复杂关系的;其次,神经网络的交互函数从数据中学习,使得该模型具有更好的通用性,可以广泛应用推广。

该模型的输出公式表达为:

y=φn(…φ1(Fs,Fkn,Fother,θf))

(4)

其中,φi表示多层神经网络的第i层,Fother就是指试题因素中的其他因素,θf表示为神经网络交互层的模型参数。

3 数据与方法

3.1 数据集描述

数据集选用的是2009-2010 ASSISTment Skill Builder Data这个最经典的认知诊断数据集,由346 860条记录以及student id,problem id,tutor mode,skill name,skill id等30个特征组成。

3.2 数据预处理

首先,对于数据集进行特征选择:根据特征相关性,筛选出user_id,problem_id,skill_id和correct 4个特征,并建立4个特征之间的联系。

接着,删除了答题数过少的学生信息,因为学生答题数过少不能让模型有效建立答题信息和能力水平之间的关系,从而无法正确对学生的知识点掌握情况做出合理诊断。

最后,将经过预处理的数据集按照7∶1∶2的比例划分训练集、验证集、测试集。

3.3 IRT模型

(1)IRT模型训练采用EM算法,对P(Xji=1 |θj,αi,βi)进行最大似然估计:

E步:根据当前的θ,α,β,求出似然函数的条件期望。

M步:根据E步给出的对数似然函数的条件期望,求出新的参数的值。

(2)模型输入:训练集。

(3)模型参数:学生个数、试题个数、迭代次数epoch、收敛条件ε。

(4)模型输出:学生能力参数θ、试题区分度α、试题难度β。

3.4 MIRT模型

(1)MIRT模型由学生个数、试题个数和试题维度这3个参数初始化而成。通过传入的参数初始化生成2.2节所述的θi,αj,dj这3个向量,分别用θ,a和b来表示。输出为:

(5)

其中,∘表示哈达玛积。

(2)模型输入:训练集。

(3)模型参数:用户个数、题目个数、维度。

(4)模型输出:被试者能力参数向量θ、试题区分度向量α和试题难度d。

3.5 DINA模型

DINA模型如图3所示。

图3 DINA模型

模型输入:

(1)学生-试题矩阵Y(学生实际作答信息)。

(2)试题-知识点矩阵Q(试题所含知识点信息)。

模型输出:学生-知识点矩阵A(记录学生是否掌握知识点)。

3.6 NeuralCD模型

NeuralCD模型如图4所示。

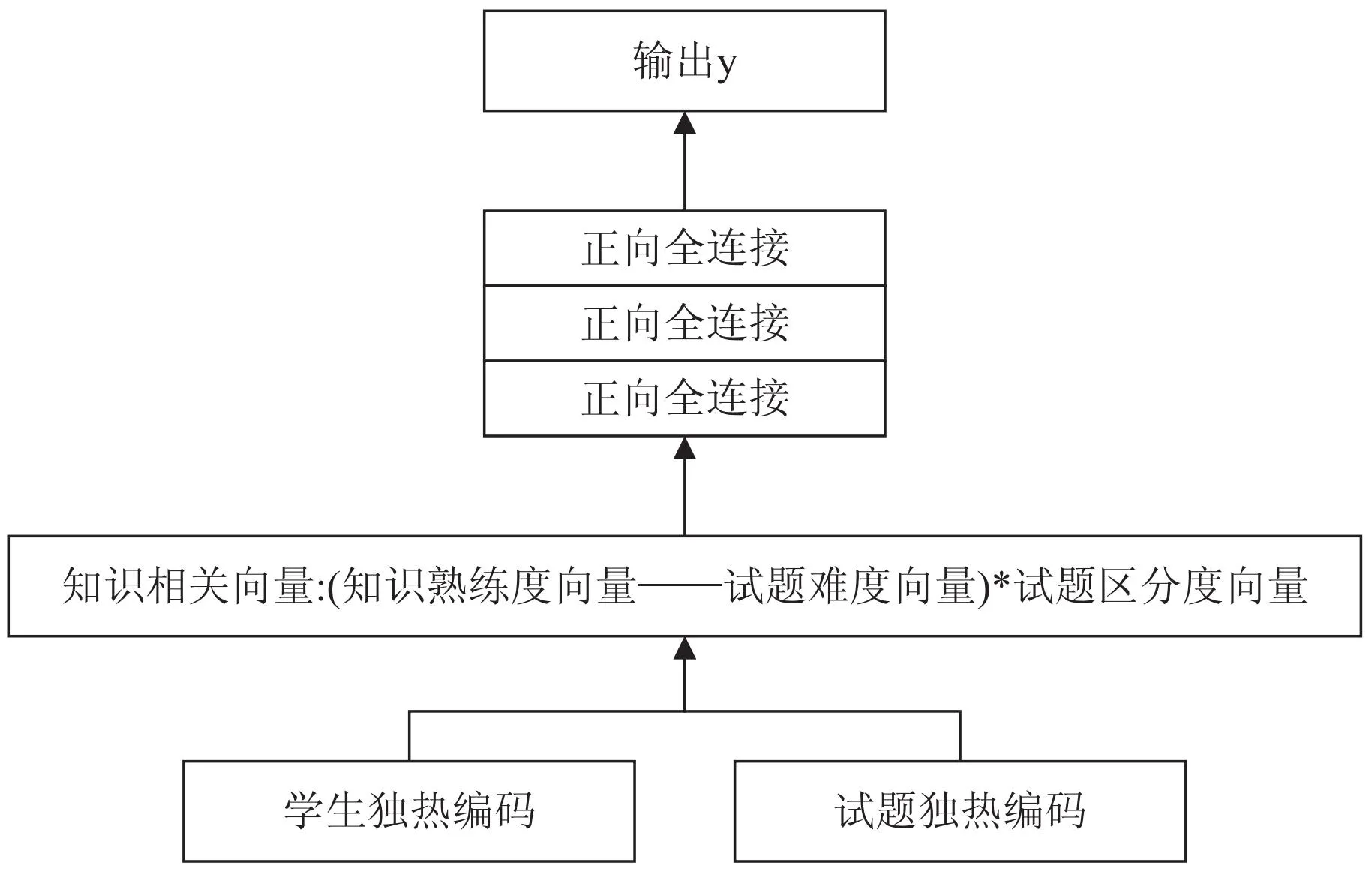
图4 NeuralCD模型

(1)学生因素。

每一位学生都用一个知识熟练度向量来表示,即上面提到的Fs是通过学生的独热编码xs乘上一个可以训练的矩阵A得到:

Fs=sigmoid(xs,A)

(6)

其中,Fs∈(0,1)1×k,xs∈{0,1}1×n,A∈Rn×k。

(2)试题因素。

对于每一道试题,Fkn知识相关向量是从传统Q矩阵中获取Fkn=xe×Q。

其中,xe∈{0,1}1×m是试题的独热编码表示,Fkn∈(0,1)1×k。

其他因素采用:试题难度hdiff∈{0,1}1×k、试题区分度hdisc∈(0,1)。

hdiff=sigmoid(xe×B)

(7)

hdisc=sigmoid(xe×C)

(8)

其中,B∈Rm×k和C∈Rm×1。

(3)交互函数。

交互层的输入受到MIRT模型的启发,输入为:

x=Fkn∘(Fs-hdiff)×hdisc

(9)

接下来的两个全连接层和最后的输出层为:

f1=φ(W1×xT+b1)

(10)

f2=φ(W2×xT+b2)

(11)

f3=φ(W3×xT+b3)

(12)

其中,φ表示激活函数,这里采用sigmoid函数。

该文采用了一个比较简单的方法来满足单调性假设:就是限制W1,W2,W3的每个元素为正。

模型的损失函数采用输出的预测值和真实值之间的交叉熵:

(13)

上述提到的A,B,C都是可训练的参数矩阵,分别代表学生对知识点的掌握程度、试题和知识点的相关度和试题的区分度。

4 实验结果

4.1 实验评价指标

该文选用Precision,Recall,F1_score和Accuracy 4个指标作为模型误差分析的评判标准:

(14)

(15)

(16)

(17)

其中,TP代表被模型预测为正类的正样本,FP代表被模型预测为正类的负样本,FN代表被模型预测为负类的正样本,TN代表被模型预测为负类的负样本。

4.2 实验结果展示

图5为4个模型在相同测试集上的Precision,Recall,F1_score和Accuracy。可以看出:

图5 不同模型测试集结果展示

在Precision上:IRT>NeuralCD>MIRT>DINA;

在Recall上:NeuralCD>IRT>MIRT>DINA;

在F1_score上:NeuralCD>IRT>MIRT>DINA;

在Accuracy上:NeuralCD>IRT>MIRT>DINA。

综合4个指标来看:

NeuralCD>IRT>MIRT>DINA

NeuralCD模型效果最好的原因是它采用神经网络为核心结构,通过神经网络强大的拟合能力使其能够从数据中学到更为复杂且贴近现实的交互函数,因此它比其余3个模型具有更强的泛用性,也具有更强的拟合能力,效果也更好。

4.3 可解释性分析

IRT模型是基于单维性假设和独立性假设的,因此在该模型中得到的学生能力参数,是一个具体的数值,该数值仅描述的是当前学生在当前这一道试题上的能力。

MIRT模型是对IRT模型的一个扩展,因为在实际的认知诊断过程中,试题之间是存在关联的。而要正确回答一道试题需要学生多方面能力间的相互作用。所以MIRT模型会得到的学生能力参数向量,表示该学生在多个维度上分别的能力值。

这两个模型理论上只是根据我们训练集的数据训练得出学生的“能力值”,尽管MIRT模型可以将维度的大小定为总的知识点个数,但是并没有体现出学生对于这个知识点的具体掌握程度。

而DINA和NeuralCD这两个模型,加入了知识点和每一道试题之间的关系,即人工标注的Q矩阵(描述了每道试题考察了哪些知识点)。

DINA模型虽然引入了Q矩阵,但是从结果上来看,将学生对知识点的掌握程度进行0/1划分,即对于一个知识点只有掌握和没掌握这两种情况。虽然有效解决了IRT模型和MIRT模型无法体现对知识点掌握情况的这一问题,但是最后体现的掌握情况过于绝对,不符合实际的教学评估标准。

最新提出的NeuralCD模型利于神经网络的架构来进行认知诊断,但是NeuralCD模型与传统的神经网络认知诊断最大的不同在于它打破了神经网络难以获得可解释性结果的特性。在输入层中包含知识熟练度向量Fs和试题相关向量Fkn按元素相乘得到的结果,即保证Fs中的每一维和Fkn中对应维的知识点是相对应的,同时在连接层通过单调性假设使得可以输出学生的知识掌握程度。

因此,从模型得到的结果的可解释性角度来看,IRT模型和MIRT模型得到的结果仅仅是学生能力的描述,没有引入试题和知识点的关系,因此并没有体现出学生对知识的掌握情况。DINA模型虽然体现了掌握情况,但0/1描述过于绝对,不符合现实情况下对学生学习状态的评估。而NeuralCD模型得到的学生认知状态是用连续值进行描述,更加准确具体,具有高度的可解释性。

所以在可解释性上:

NeuralCD>DINA>MIRT>IRT

4.4 结果分析

经过对4个模型的分析,得出以下结论:

(1)IRT模型、MIRT模型和DINA模型都是传统的认知诊断模型,其中IRT模型和MIRT模型基于连续值,DINA模型基于离散值。而NeuralCD模型是基于神经网络架构的。

(2)在交互函数上3个传统认知诊断模型依赖于人工所定义的函数,采用逻辑回归函数或者是向量的内积,而NeuralCD模型是通过神经网络去学习数据,不再依赖于人工定义的交互函数。

(3)IRT模型和MIRT模型诊断的结果表现为学生的“能力”值。因为两个模型并未引入Q矩阵,所以并不能准确体现出学生对知识点的掌握情况。

(4)DINA模型和NeuralCD模型引入Q矩阵后实现了学生对于知识点的掌握,但是DINA模型得到学生对于一个知识点掌握的结果只是0(未掌握)和1(掌握),而NeuralCD模型得到的结果是[0,1]这个区间内的值,符合现实教育中对于知识点的掌握是阶段性的实际情况。

(5)将NeuralCD模型的Q矩阵变为一个等维度的单位矩阵,将多层神经网络求和后再使用sigmoid函数激活,NeuralCD模型就变成了MIRT模型。

(6)IRT模型诊断的其实是学生的单一做题记录,MIRT模型、DINA模型和NeuralCD模型诊断的是学生的多个历史做题记录,是多交互的诊断过程。

上述结论也并不表示NeuralCD模型就可以完全替代其它3个模型所具有的效果。从目前在教育领域的认知诊断来看,有整体的诊断,也存在对具体一个阶段的诊断,因此,对于认知诊断模型的选取有如下建议:

(1)NeuralCD模型适合用于大样本数据,是对学生之前历史做题记录的总结诊断,并且知识点覆盖是较大的,全面的诊断工作。

(2)IRT模型适合用于在教育中对具体一个知识点相关的习题测试中,根据学生对习题回答的正确与否来估计学生在这一知识点上所具有的能力值。

(3)MIRT模型适合用于在知识点个数已知,考查学生在与这些知识点相关联的习题中的作答情况,分析出学生在这几个知识点上所具有的能力值。

(4)DINA模型适合用于对二值计分测验进行认知诊断,如一场考试中的判断题只有两种答案的场景,用DINA模型可以获得较高的认知准确度。

5 结束语

首先,介绍了认知诊断的基本概念、研究目的、历史发展以及研究现状;接着,基于研究开源的数据资料建立了IRT等4个认知诊断模型,并对4个模型在相同数据集上的认知准确度和模型可解释性能力进行对比;最终,得出NeuralCD模型认知准确度最高且具有最好的可解释性的结论。此外,通过调研和实验总结出不同模型的适用场景,为认知诊断研究提供了新视角。

但是,该文仅研究了学生的答题准确率与学生能力水平以及题目信息的关系。未来,希望探究不同因素对学生知识点掌握程度的影响以及学生掌握知识点的普遍练习次数等,从多因素多角度进行认知诊断,推动认知诊断研究领域的发展。