改进混合萤火虫算法求解CVRP

白雪媛,张 磊,李 琳,武文喆

(1.沈阳航空航天大学 理学院,辽宁 沈阳 110136;2.沈阳航空航天大学 电子信息工程学院,辽宁 沈阳 110136)

0 引 言

有容量约束车辆路径问题(CVRP)是NP-hard问题,其目标函数为车辆服务完全部客户后,所有车辆所走路程最短或所用费用最少[1]。目前,该问题求解方法有精确算法、启发式算法和元启发式算法。

因使用精确算法在可接受时间内无法求得大规模CVRP最优解,国内外学者多采用启发式或元启发式算法进行求解[2]。黄戈文等[3]利用整数编码和先路由后分组实现解的转换,提出自适应遗传灰狼优化算法(AGGWOA)以研究CVRP。邵可南等[4]提出模拟退火-遗传混合算法(GA-SA)解决带硬时间窗和容量约束的单中心车辆路径问题。Francesco等[5]用K-Means聚类提出CC-CVRP,将客户点分为不同集群,将CVRP转化为多个TSP。

萤火虫算法(Firefly Algorithm,FA)是Yang[6]开发的启发式算法。FA和不同方法结合,衍生出许多解决NP-Hard问题的算法[7]。标准萤火虫算法因每只萤火虫迭代寻优时都会随机移动,寻优搜索过程复杂,算法收敛速度较慢,易陷入局部最优。为提高算法性能,许多学者对FA做出多方面改进。

Mohammadi等[8]用FA在考虑订单的交货时间和成本基础上最小化总完成时间。李媛媛等[9]以K-Means聚类中心作为寻优萤火虫,结合邻域与随机吸引(N-R吸引)提出了KNRFA模型。闫军等[10]将K-Means聚类和Q-leaning自启发式引入蚁群算法,求解带时间窗同时取送货车辆路径问题。

Li等[11]在FA中加入自适应对数惯性权重,用步长减小因子动态调整随机步长,提出LWFA。Mohsen等[12]为解决TSP将FA与局部搜索算法(2-opt和3-opt),遗传算法中的变异交叉因子相结合,提出离散混合萤火虫算法(HDFA)。Matthopoulos等[13]结合贪婪算法提出混合萤火虫算法,解决异构固定车队VRP。Jaradat等[14]首先利用K-Means聚类将TSP分为子问题,再利用FA在每一类中寻找最优路径。

Altabeeb等[15-16]将FA与局部搜索(改进的2-opt和2-h-opt)、变异交叉算子结合提出CVRP-FA,用田口方法统计确定参数的最佳值。但因CVRP-FA在2-h-opt处理后只接受有改进方案,算法易陷入局部最优,无法产生更好的解,故将2-h-opt作为一种变异,而非局部搜索,提出CVRP-CHFA。该方式使算法可接受2-h-opt产生的所有解。该算法还引入合作岛模型概念,保持解的多样性,避免算法陷入局部最小值,达到加快算法收敛速度的目的。

该文提出一新的混合萤火虫算法(KM-HFA)求解CVRP。引入有约束条件的K-Means聚类,以聚类结果为基础构建较好可行解作为萤火虫寻优初始解。结合部分匹配交叉和Intra-Swap,Inter-Swap变异算子,防止算法陷入局部最优。引入2-opt和2H-opt局部搜索算法提高算法收敛速度,将算法用于求解标准算例。

对A,B,P,E组数据集72组算例,算法KM-HFA所得可行解比文献[5]提出的CC-CVRP、文献[13]提出的HFA结果好。当客户点逐渐增多时,KM-HFA的计算稳定性显著优于HFA,最优解与经典解的百分比差异要比另两种算法求解的百分比差异小得多,算例验证了文中算法的有效性。

1 CVRP描述和数学模型

CVRP是经典VRP,其定义在图G(N,E)上,节点集为N={0,1,…,n}。节点0为仓库(配送中心),节点{1,2,…,n}表示需服务客户点,i∈N{0}的需求为qi,从节点i到j的运输成本为Cij。K为仓库所拥有的车辆集合,Q为车辆最大载重。

CVRP数学模型描述如下:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

目标函数(1)为最小化车辆总运输成本,约束(2)和(3)保证节点仅被访问一次,约束(4)保证车辆运输过程中载重不超过车辆最大载重,约束(5)保证车辆从仓库出发并最终回到仓库。

2 改进混合萤火虫算法

FA作为元启发式算法,随机生成初始解,但寻优结果在很大程度上依赖初始解,初始解较好时,其寻优结果会更好。该文提出的KM-HFA先引入带约束条件K-Means聚类,以聚类结果为基础,构建较好可行解作为萤火虫寻优初始解,克服寻优结果依赖初始解的问题。为增加萤火虫种群的多样性,将GA的部分匹配交叉和2H-opt交换算子与FA结合,进行可行解间操作。最后,引入局部搜索算法2-opt和两种变异算子提高算法收敛速度,防止其陷入局部最优。KM-HFA的伪代码如下,各步骤将在后续部分中具体说明。

KM-HFA算法

Begin

Input: 目标函数f(S);

Output:全局最优解S*;

Initialize:MI,C-R,M-R;

t=0; /*t代表迭代次数*/

初始种群P:S=(S1,S2,…,Sn);

Fori=1-P-Sdo

计算萤火虫Si的目标函数f(Si);

找出初始种群内最优解S*;

End for

计算汉明距离和亮度

whilet≤MI do

fori=1 toP-Sdo

forj=1 toido

IfIi>Ijthen

2H-opt procedureSi;

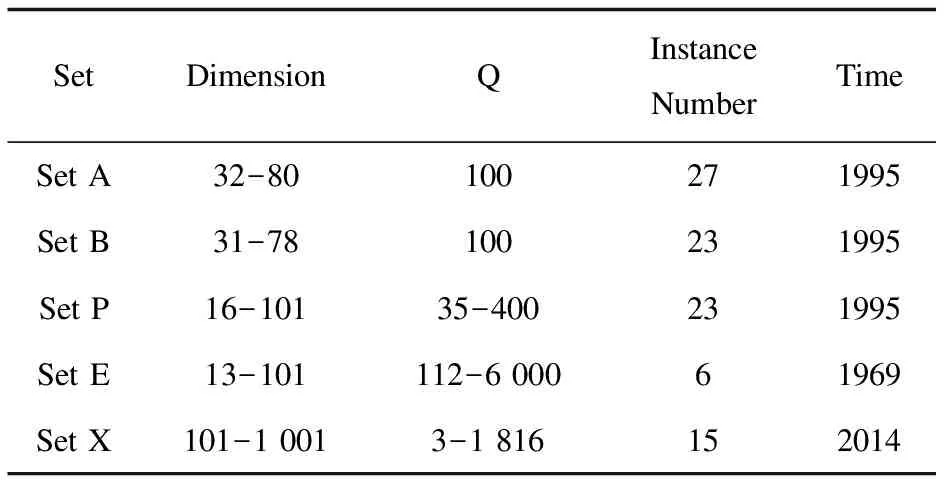
If rand

PMX procedureSi;

End if

2-opt procedureSi;

mutation procedureSi;

End if

End forj

End fori

排序,找出当前最优萤火虫;

t=t+1;

End while

返回全局最优解S*;

End

2.1 路径编码转换

在计算过程中,可行解由K条(K为所用车辆数目)路径组成,每条路都由n个点构成,表示该路径所分配到的客户点个数。该文在计算萤火虫亮度和可行解之间的操作时,需将多路径CVRP转换为单路径TSP,进行路径编码转换(见图1)。在完成可行解间操作后,编码方式转换回多路径编码,再对各可行解内的路径进行局部搜索和变异操作。

图1 路径编码转换

2.2 有约束的K-Means聚类构建初始解

标准FA的寻优随机生成初始解,寻优结果对初始解有较强依赖性,当初始解较好时,最终可找到更好解。该文先引入K-Means聚类,聚类后的客户点间距离较接近,再进行路线构建。聚类使距离较接近的客户点归为一类,利用该特性进行路线构建得到的初始解比随机生成的初始解好,将聚类后构建的解为启动萤火虫寻优算法的初始解。

2.2.1 K-Means聚类

K-Means聚类采用距离作为对象相似性的评价指标,两个点离得越近就越相似,相似度和距离成反比。两点间距离采用欧氏距离来计算:

(7)

每类有且只有一个聚类中心,该中心是类内所有数据的平均值,计算点与聚类中心的距离,判断出该点属于哪一类。最终所有数据点被分为独立的,由距离相近的点所组成的K类。K-Means聚类的K值需预先设定。为满足车辆载重约束,K值由客户点总需求和车辆最大载重计算,结果向上取整,即:

(8)

K-Means聚类的步骤为:

(1)计算两点间欧氏距离;

(2)由公式8设定聚类数K,并随机选取K个客户点作为聚类中心Ci;

(3)将客户点分配给距离其最近的聚类中心,直至所有客户被分为K类;

(4)更新类的中心点,并重复步骤3直至簇不再发生变化。

2.2.2 构建初始种群

初始种群由多个可行解构成,每个可行解都按如下步骤进行构建:

(1)派出一辆车从仓库出发随机选取一类CLi进行服务;

(2)在该类内随机选择一个客户点并将该客户点从列表删除,以免重复服务;

(3)将选中的客户点加入到该路径;

(4)判断加入该客户点后的车辆是否超载,若车上的载重未超过最大载货量则重复步骤2和步骤3;否则将车辆返回仓库,并派出下一辆车继续服务;

(5)当该类客户都服务完,找到和该类中心最近的下一类中心Cj,对CLj类内的客户进行服务;

(6)重复操作至数据集内客户点都服务完。

上述步骤每进行一次则得到一个可行解,多次重复后得到初始种群,即后续萤火虫寻优算法的初始解。对每个可行解计算目标函数,即车辆行驶的总距离。初始种群中,萤火虫的亮度和目标函数值成反比,目标函数值越大亮度越小,目标函数值较低的可行解就是更具吸引力的萤火虫。根据亮度对初始种群内的可行解进行排序,目标函数值最小的萤火虫作为当前的最优解Sbest。

2.3 亮度计算

该文使用汉明距离(Hamming Distance,HD)计算寻优过程中的萤火虫亮度。HD为两相等长度字符串对应位元素不同的数量,即比较两种可行解对应位置的客户是否相同,若客户相同则两者间的汉明距离不增加,若不同则汉明距离加1。

图2展示了计算汉明距离的例子,Si和Sbest都有12个客户点,在客户点中,对应位不同的客户共7个,两者之间的汉明距离为7。

图2 汉明距离计算

设萤火虫i的亮度为1到HD之间的随机数:

Ii=Random(1,HDi,best)

(9)

比较两只萤火虫的亮度,对亮度大的萤火虫进行后续操作。

2.4 可行解间的交换

2H-opt交换和部分匹配交叉都是针对整个可行解进行处理的变换,涉及到路径转换,所以将2H-opt和部分匹配交叉放在一起进行操作,可避免多次路径编码的转换增加算法复杂度。在可行解间进行2H-opt交换和部分匹配交叉可增加萤火虫种群的多样性,扩大寻优范围,增加找到更优解的可能性。

2.4.1 2H-opt交换

2.4.2 部分匹配交叉

交叉是遗传算法中的操作算子,它可以挖掘种群的多样性,克服启发式算法容易陷入局部解的问题。该文将Si和Sbest作为父代,对两者进行部分匹配交叉(Partially Matching Crossover,PMX)操作,具体步骤通过图3中的例子展示。

图3 部分匹配交叉

在两个父代中随机选取两者中相同位置的基因片段进行交换,图中灰色片段被交换;如图3所示,由于交换后染色体中可能会出现如基因5,8,3等与交换片段所重复的基因,所以需要染色体进行重复检测并进行去重处理;交换的片段建立映射关系,如基因5的映射点为基因3;重复的点将会由其映射点替换,注意此时替换的是未被交换的基因,被交换的基因不做任何处理;将重复的点全部替换完成后,最终形成两个子代。交叉后得到两子代,计算两子代目标函数值,与Si目标值比较,若子代中有更小的解则更新Si,否则不更新。

2.5 可行解内部交换

可行解内变换利用局部搜索和变异算子对可行解内路径进行处理,不仅可以提高算法的收敛速度,维持萤火虫种群的多样性,从而获得更优可行解,还能避免萤火虫算法寻优过程陷入局部最优。

2.5.1 局部搜索

用局部搜索2-opt算子在种群内产生新可行解。在可行解内随机选取某一条路径,在该路径中随机选取两个客户点,将这两点间的子片段进行反转操作后重新插入到该片段中,即可产生新的可行解。

2.5.2 变异算子

变异能维持萤火虫种群的多样性,一定程度克服FA易陷入局部最优的缺陷。给定变异率,在区间(0,1)内产生随机数,当随机数小于设定变异率,利用变异算子产生新的可行解。该文采用两种变异算子:Intra-Swap是在可行解内随机选取一条路径r1,随机选取该路径的两个点c1,c2进行交换得到新的可行解;Inter-Swap是在可行解内选取两条路径r1,r2,在r1中随机选择一客户c1,在r2中随机选择一客户c2,将c1,c2进行交换,得到新的可行解。

3 实验及结果分析

文中算法用Python在Intel i5 1.8 GHz和4 GB内存计算机上实现。测试实例包括以下在http://vrp.galgos.inf.puc-rio.br上公开提供的实例:客户数量在100以下的小规模数据集A,B,P,E,共79组实例;客户数量为101-1 001的中规模数据集X,选取其中15组实例。KM-HFA对每个实例独立运行10次,最大迭代次数为1 000。该算法参考了Altabeeb等[17]通过田口统计实验所提出的参数值,种群数为20,变异率为0.1,交叉率为0.95。

表1列举了文中所用数据的相关信息,其中Set为数据集名称,Dimension为数据维度,Q表示该数据所用车辆的容量,Instance Number为从数据集中选取实验实例的个数,Time为该数据集创建时间。

表1 数据相关信息

文献[5]利用K-Means聚类将客户分为不同集群,提出CC-CVRP算法,把CVRP转为TSP,对Set A, X进行求解;文献[13]结合贪婪算法提出HFA对Set A, B, P, E进行求解。该文将KM-HFA同上述两种算法进行比较,比较各算法得出的最优解所需的路径距离(Best)及与网站公布的已知最优解(B-K)之间的百分比差异(Gap/%)。

表2～表5为KM-HFA同CC-CVRP和HFA计算79组小规模实例的结果比较,表6为KM-HFA与CC-CVRP计算中规模数据集X中15组实例结果比较。其中,第一列为CVRP实例数据,第二列为公布的已知最优解,第三、四列为HFA最佳结果和它与最优解的百分比差异,最后两列为KM-HFA求得的最好解和它与最优解的百分比差异。表中加粗部分为与其他算法相比该算法结果更好,“*”代表和经典解有相同路径数的更优新解,“**”代表比经典解增加一条路径,车辆行驶总距离更小的新解。

表2 数据集A的KM-HFA与其他算法结果比较

由表2知,对A组27个实例,KM-HFA的结果26个优于HFA和CC-CVRP的解,且A-n33-k5的解几乎接近经典解。值得注意的是,对实例A-n33-k6和A-n37-k6,在同路径数条件下,KM-HFA找到了比经典解更好的新可行解。路径展示如图4所示。

(a)A-n33-k6

对表3展示的B组23个实例,KM-HFA可行解有21个优于HFA得到的可行解,且计算B-n50-k8的解几乎接近经典解。对B-n31-k5和B-n34-k5两个实例,文中算法得到了与经典解相同的结果。

表3 数据集B的KM-HFA与混合萤火虫结果比较

KM-HFA和HFA对P组23个实例计算结果如表4所示,KM-HFA可行解有21个显著优于HFA的可行解。对实例P-n21-k2和P-n22-k2,两种算法都搜寻到经典解。KM-HFA算法在计算P-n16-k8,P-n19-k2,P-n20-k2时,在不增加路径数的同时得到比经典解更好的方案;在计算P-n22-k8,P-n23-k8两组实例时,KM-HFA算法在比经典解增加一条路径的前提下,找到了车辆总行驶距离更小的解。

表4 数据集P的KM-HFA与混合萤火虫结果比较

各实例对应解为:P-n16-k8共8条路线:0-5-14-0; 0-1-0;0-4-11-0; 0-3-8-0; 0-10-12-15-0; 0-7-9-13-0; 0-2-0; 0-6-0; P-n19-k2共2条路线: 0-18-5-13-15-9-7-2-6-1-0;0-4-11-14-12-3-17-16-8-10-0; P-n20-k2共2条路线: 0-19-5-14-16-9-13-2-7-6-0;0-1-10-8-17-18-3-12-15-11-4-0; P-n22-k8共9条路线0-9-2-1-10-0;0-18-17-0;0-14-0;0-16-0;0-5-7-0;0-19-21-20-0;0-4-3-6-8-0;0-11-13-0;0-12-15-0; P-n23-k8共9条路线: 0-5-14-22-0;0-6-16-0;0-7-20-0;0-8-2-0;0-4-11-0;0-21-0;0-3-19-18-0;0-17-9-13-0;0-1-10-12-15-0。

表5呈现E组6个实例结果,其中KM-HFA的可行解有4个明显优于HFA的解。但在计算E-n33-k4实例时,HFA搜寻到经典解,但是KM-HFA得到的最优可行解也与经典解非常接近。

表5 数据集E的KM-HFA与混合萤火虫结果比较

表6是X中15个实例结果,其中KM-HFA的可行解有7个都优于CC-CVRP的解;但CC-CVRP有8组实例结果更好;表明KM-HFA在计算中规模数据实例时,计算质量有所降低。分析数据发现,是因为中规模数据相比于小规模数据,客户数量较多、位置较分散。客户点较分散时,K-Means聚类不能将客户进行更有效的分类,导致萤火虫算法不能以较好的初始解开始寻优,算法计算性能下降。

表6 数据集X的KM-HFA与CC-CVRP结果比较

4 结束语

该文提出KM-HFA求解CVRP。通过引入K-Means聚类算法获得更好初始解,将所得解作为萤火虫寻优初始解。结合遗传算法中的PMX交叉在种群内产生新的子代,以及两种变异算子Intra-Swap、Inter-Swap,防止算法陷入局部最优。为提升萤火虫种群的多样性,增强算法的局部搜索能力,加入2H-opt交换算子和2-opt局部搜索算子。

采用小规模数据79组,中规模数据15组,共94组数据检验KM-HFA的计算效果。实验结果表明:在72组小规模实例中,KM-HFA得到的可行解比文献[5]提出的CC-CVRP、文献[13]提出的HFA得到的结果好。且当客户点增多时,KM-HFA计算稳定性显著优于HFA的,得到的最优解与经典解的百分比差异要比另外两种算法求得的解的百分比差异小得多。在15组中规模实例中,由于客户数量较多、位置较分散,K-Means聚类不能将客户进行更有效的分类,导致萤火虫算法不能以较好的初始解开始寻优,最终使KM-HFA的计算质量有所降低。

KM-HFA在计算5组小规模实例A-n33-k6,A-n37-k6,P-n16-k8,P-n19-k2,P-n20-k2时,不增加路径数的同时得到比经典解更好的方案。在计算实例P-n22-k8和P-n23-k8时,比经典解路径数增加了一条的前提下,找到了车辆行驶总距离更小的解。

提出的KM-HFA还可应用于解决其他VRP,例如VRPTW、绿色车辆路径问题等。未来将研究如何把该算法与其它精确求解算法相结合,得到运算效果更好的混合算法。