基于非负矩阵分解的均方残差多视图聚类算法

郝敬琪,胡立华,张素兰,张继福

(太原科技大学 计算机科学与技术学院,山西 太原 030024)

0 引 言

聚类分析作为机器学习的主要研究分支,是一种广泛使用的无监督学习技术。在没有使用任何先验知识的条件下,按照对象间的相似程度,将不同的对象划分为不同的簇,确保每个簇内的对象尽可能相似,而不同簇间的对象尽可能相异。目前,聚类分析已广泛应用在科学数据分析[1]、商业[2]、生物学[3]、医疗诊断[4]、文本挖掘[5]等领域。

多视图聚类(Multi-View Clustering,MVC)主要包括基于k-means的方法[6]、基于图的方法[7]以及基于子空间的方法[8]等。相较单视图聚类,多视图聚类方法充分考虑到数据的多样性和多面性,能够处理异常值和噪声,从而获得更好的聚类性能,因此成为聚类分析中的研究热点。然而,针对高维、海量的数据,现有的多视图聚类方法中仍然存在以下问题:(1)多视图数据集维度过高时,现有的多视图聚类方法很难发现隐藏信息;(2)大多数多视图方法融合过程仅考虑各单视图内部的局部特征,无法平衡每个视图的重要性。

针对上述问题,结合非负矩阵分解和均方差残差思想,提出了一种基于非负矩阵分解的均方残差多视图聚类方法。该方法首先采用非负矩阵分解思想,在相关误差矩阵中加入鲁棒低秩约束,使系数矩阵的内部结构信息和误差矩阵中一些有用的判别信息得到充分的挖掘,并解决维度过高无法发现隐藏信息的问题;其次利用均方残差对每个视图结构进行自适应融合,使不同视图的结构在算法更新过程中得到融合和改变,从而平衡各单视图之间的重要性。

论文的创新点包括:(1)设计了一种改进的非负矩阵分解方法,提高单视图矩阵分解的鲁棒性和稀疏性;(2)提出了一种自适应单视图融合方法,改进了各单视图之间融合的效果;(3)结合上述方法,提出了一种基于非负矩阵分解的均方残差多视图聚类方法;(4)采用标准数据集和古建筑图像,验证了算法的有效性。

1 相关工作

随着信息技术的飞速发展,数据的规模出现海量、多源、异构、高维等特点。针对上述数据,传统的单视图聚类存在聚类效率低、聚类效果差等问题,而多视图聚类方法可从不同角度分析数据,进而提高聚类效果,因此,受到了研究者的广泛关注。

目前,多视图聚类算法可分为三类:基于k-means的方法、基于图的方法以及基于子空间的方法。

(1)基于k-means的方法:该方法首先对多视图数据的各单视图采用k-means聚类生成单视图聚类结果,然后对各单视图的聚类结果进行融合,最后得到最终聚类结果。典型方法有:2004年Bickel等人[9]提出了扩展的k-means的方法,处理具有两个条件独立视图的情况。但是该方法只能处理两个视图的情况,无法处理三个或更多视图的情况。为了解决三个或更多视图聚类的问题,2016年Rai等人[10]将部分视图聚类(PVC)算法扩展到k部分视图场景。其次扩展了k部分视图算法,包括将视图拉普拉斯正则化。使得该算法能够利用每个视图中数据分布的内在几何结构。2018年Zhang等人[11]提出了一种基于k-means的两级加权融合多视图聚类方法,有效解决了三个及以上视图的情况,但没有考虑各单视图的结构和不同视图的融合。

(2)基于图的方法:该方法的核心思想是将多视图聚类问题转化为图分割问题[12]并进行谱聚类操作。但是,该类算法也存在一些问题,图谱聚类的最终结果完全依赖于构造的相似矩阵,然而不同的构造方法会影响聚类结果,因此构造理想的相似矩阵成为研究热点[13]。近年来,许多学者对谱聚类算法中相似矩阵的构造方法做了进一步研究与改进。典型方法有:2000年Shi等人[7]通过高斯核函数构造相似矩阵。2001年Ng等人[14]提出NJW算法,通过高斯核函数构造相似矩阵,并采用全连接构造方法。2010年Zhang等人[15]利用两个样本点之间的局部密度求相似矩阵。2016年Nie等人[16]通过局部连通性为每个数据点分配自适应和最优邻居来学习相似矩阵。2018年Xie等人[17]采用样本点与样本点的近邻点之间的欧氏距离作为局部标准差构造相似矩阵。2018年Zhan等人[18]联合优化图矩阵,充分利用视图之间的数据相关性进行多视图聚类,并且可以处理任意数据集,即使它们包含负值。2020年Liang等人[19]构造每个视图的邻接图来保持每个视图的几何信息,并推导出相应的基于交替迭代规则的乘法更新算法。然而这些文献中构造的相似矩阵都是固定的,不能很好地挖掘和利用数据结构。

(3)基于子空间的方法:该方法试图揭示多视图共享的公共潜在子空间,子空间多视图方法利用矩阵分解来设计。利用各种矩阵分解方法,可寻找出隐藏在原始数据中的低维结构,便解决了“维度魔咒”的问题。典型方法有:2016年Zhou等人[20]提出稀疏多视图矩阵分解算法,旨在根据方差的视图特异性对特性进行优先级排序。2017年Zhao等人[21]提出了一种通过图正则化半非负矩阵分解的深度多视图聚类算法,关键是通过半非负矩阵分解构建深层结构,以寻求具有一致知识的公共特征表示,从而促进聚类。2020年Chen等人[22]提出了一个统一的框架,联合了学习潜在嵌入表示、相似信息和聚类指标矩阵。然而,上述方法应用到高维海量多视图数据中,存在以下问题:利用非负矩阵分解的子空间聚类算法进行降维时,不仅会丢失数据的隐藏信息,而且降维维度的不确定性也导致了后序算法的不稳定性;并且大部分多视图聚类算法没有平衡每个视图的重要性,仅仅考虑了各个视图内部的局部特征,没有考虑到视图之间的联系。

2 基础知识

2.1 非负矩阵分解

给定矩阵X∈Rm×n,m为对象特征个数,n为对象数量,将其非负矩阵分解[23]为基矩阵U∈Rm×k和系数矩阵V∈Rk×n,k为分解维度,具体定义如下:

定义1(非负矩阵分解):给定一个矩阵X,其非负矩阵分解过程可描述为:

X≈UV

s.t.U≥0,V≥0

(1)

定义2(非负矩阵的误差Ex):Ex为给定矩阵X与基矩阵系数矩阵乘积UV之间的误差,Ex的计算公式如下:

s.t.U≥0,V≥0

(2)

其中,*表示点积。

2.2 流形正则化

流形正则化[24]是由Tenenbaum等人于2000年提出的一种方法,具体定义如下:

定义3(流形正则化O2):设Vi和Vj表示系数矩阵的第i列和第j列。利用F-范数计算列之间的偏差,以测量多视图中的低维表示的平滑度。流行正则化过程定义为:

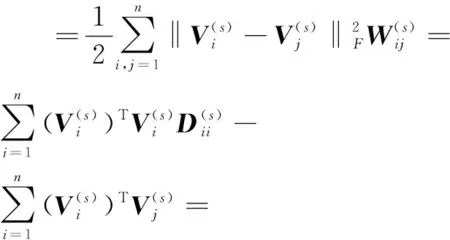
(3)

2.3 希尔伯特-施密特独立性准则

希尔伯特-施密特独立性准则(Hilbert-Schmidt Independence Criterion,HSIC)[25]是一种基于核的独立性度量方法,具体定义如下:

定义4(HSIC的一般形式):给定n个样本点和不同视图V(s),V(w),则视图V(s)和视图V(w)的关联性HSIC被定义为:

HSIC(Z,V(s),V(w))=

(n-1)2tr(K(s)HK(w)H)

(4)

其中,Z:={(x1,y1),(x2,y2),…,(xn,yn)}∈V(s)×V(w),hij=δij-1/n是中心矩阵,δij为n阶单位阵,K(s)和K(w)是两个内积矩阵。

3 文中算法

3.1 问题定义

基于图正则化概念分解的多视图聚类方法采用非负矩阵分解方法实现数据从高维到低维的映射表示,利用视图之间的数据相关性进行多视图聚类,从多视图数据中学习亲和图,以解决视图之间的相关性问题,同时避免利用单个图构造亲和图。然而针对高维海量数据,该算法具有以下问题:(1)非负矩阵分解将矩阵X分解为基矩阵U和系数矩阵V的乘积,但是,此过程是近似分解,导致数据缺失从而增加矩阵分解的误差;(2)使用低维系数矩阵V代替高维矩阵X进行多视图聚类时,视图内部潜在信息存在难以解释的问题,使得低维数据不能完全映射高维数据;(3)现有的多视图聚类算法不能充分挖掘视图之间的差异性和互补性,导致了聚类结果不准确。

3.2 算法步骤

针对上述问题,提出了基于非负矩阵分解和均方残差的多视图聚类方法(MSRNMF)。首先,对多视图数据中各单视图矩阵进行改进后的非负矩阵分解,得到各单视图的系数矩阵;其次,为了保持多视图内部结构和视图之间的联系,使用流形正则化和HSIC以自适应的方式获得潜在表示,得到改进后的系数矩阵;然后,对多视图下各单视图进行谱聚类;最后,依据各单视图聚类结果,再结合均方残差的思想对聚类结果进行融合,得到最终多视图下聚类结果。算法流程如图1所示。

图1 算法流程

3.2.1 系数矩阵的改进

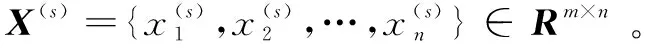
根据非负矩阵分解的特点,矩阵X(s)可以分解为U(s)和V(s)。非负矩阵分解是一种近似分解,为了减少分解过程中的误差,很多算法常使用定义2最小化误差矩阵。然而,Ex忽视了数据间的稀疏性和鲁棒性,增加了矩阵的误差。

针对上述问题,在误差Ex中使用L21范数代替F-范数,以提高分解的稀疏性和鲁棒性。为了充分利用数据的内在信息,添加了给定矩阵X和基矩阵U之间的误差,即误差矩阵Eu,并对其使用核范数。结合上述改进思想,提出了一种改进的非负矩阵误差。具体的:

定义5(改进的非负矩阵误差O1):

O1=‖Ex‖21+‖Eu‖*

(5)

s.t.Ex=X-UV,Eu=X-U,U≥0,V≥0

由于改进的非负矩阵分解没有考虑视图内部数据间结构特征的完整性,低维潜在表示存在难以解释的问题,进而导致视图内部联系不紧密、结构不一致。为保证每个视图内部的局部几何结构,针对上述问题,利用流形正则化以保持矩阵内部结构的不变性。为了进一步加强不同视图之间的相互学习和双向融合,添加了HSIC模块,以便于在模型优化过程中实现视图之间的互连、相互学习和信息集成。

综合改进的非负矩阵分解、流行正则化和HSIC三部分知识,更新系数矩阵V(s)的目标函数可由以下公式给出。

定义6(更新系数矩阵V(s)的目标函数):

(6)

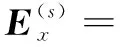
式中有三个正则化参数,其中λ1用来测量稀疏表示的重要性,(α(s))γ和λs分别是平滑项和反向回归项的权衡相关性。更新V(s)需固定变量U(s),Ex(s),Eu(s),(α(s))γ,则式6的优化问题转化为:

(7)

其中,λ和μ是拉格朗日参数。将式7中关于V(s)的导数设为0。根据Karush-Kuhn-Tucker条件,可以写成:

F1V(s)+V(s)F2=F3

F1=μ(U(s))TU(s)+λ,F2=α(s)L(s)+λs

(8)

3.2.2 多视图聚类融合

对V(s)利用谱聚类算法得到各单视图下的聚类结果C(s)。接着利用双聚类的概念,计算具有高相似性分数即均方残差得分的子集。通过向重复簇所在矩阵中添加非重复簇的方式,判断添加后相似性是否提高。

定义7(均方残差得分):对于矩阵C(s),假设X为一组行集,Y为一组列集,cij为矩阵C(s)第i行j列下的数据值,I∈X和J∈Y是行列的子集,子矩阵(I,J)具有均方残差得分H(I,J):

(9)

计算各单视图的聚类结果C(s)中重复簇的均方残差得分H(I,J)并取均值,将其定义为XH。接着考虑是否将非重复簇添加到重复簇所在的矩阵中,计算添加后的均方残差得分H(I,J)并取均值,将其定义为YH。若XH-YH<θ,则将此簇添加入重复簇中,如此迭代,则可得到最终结果。在后续实验中得出θ=0.02效果最佳。

4 实验结果与分析

4.1 环境设置

古建筑多视图数据集构造方面采用Ubantu 18.04.6 LTS操作系统,intel Core i7-7800X处理器 (CPU@3.50 GHz×12),32 GB内存,选择Python语言进行实验。多视图聚类算法采用Windows11操作系统,AMD处理器(CPU@3.25 GHz×8), 16 GB内存,选择Matlab语言进行实验。

4.2 数据集

为了验证算法的效率,以5个标准的多视图数据集和古建筑数据集为对象进行验证。

4.2.1 标准数据集

(1)ORL数据集:包括40个不同主题的10个不同灰度人脸图像。

(2)3-Sources数据集:涵盖BBC、路透社和《卫报》报道3个在线新闻来源,包含416例病例。

(3)MSRCv1数据集:由7类210幅场景识别图像组成。

(4)Yale数据集:由15个受试者的165张原始像素图像组成。

(5)BBCSport 数据集:来自BBC体育网站的体育新闻文章的集合,包含282个报告的3个视图的数据集。

4.2.2 古建筑数据集

古建筑数据集采用中科院金光寺数据集中的金光寺主建筑图片进行实验,如图2所示。

图2 金光寺图片

对上述两幅古建筑图像进行多视图数据集的构建,首先对每幅图像选取11 320个特征点,其次提取特征点的位置、颜色、纹理、轮廓、领域和SIFT特征,即可构建一个高维海量的多视图数据集。

4.3 评估指标

对于定量性能评估,使用以下7个众所周知的评估标准。它们分别是聚类准确度(ACC):用于衡量聚类算法得到的聚类结果的准确率,取值范围为0到1;归一化信息(NMI):用于衡量两个聚类簇中所包含的数据点之间的相似性,取值范围为0到1;纯度(purity):反映聚类结果中所有样本中被正确聚类的样本比例,取值范围为0到1;精度(precision):表示预测为正确的数据中,真实值为正确的比例,取值范围为0到1;召回率(recall):表示在所有的真实值为正确的数据中,预测正确的比例,取值范围为0到1;F-score:将精度和召回率结合起来综合评价分类或聚类结果的指标,取值范围为0到1;调和兰德指数(ARI):用于衡量聚类算法的聚类结果与真实类别之间的相似度的一种常用外部评价指标,取值范围为-1到1。

4.4 实验结果

4.4.1 标准数据集下的结果

将MSRNMF与部分多视图聚类方法(GPMVNMF)[10]、多视图聚类的自适应结构概念分解方法(MVCF)[18]、图正则化部分共享非负矩阵分解方法(GPSNMF)[19]、基于深度矩阵分解的多视图聚类方法(DMF)[21]、潜在嵌入空间中的多视图聚类方法(MCLES)[22]进行比较,结果如表1～表5所示。

表1 ORL数据集实验结果

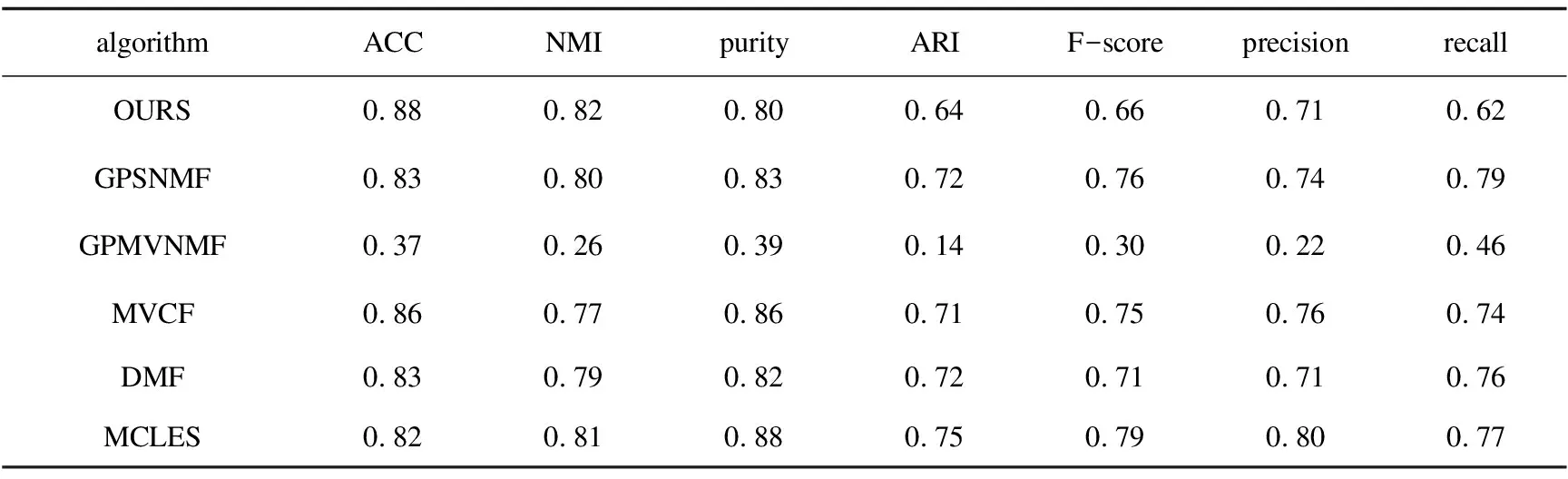
表2 MSRCV1数据集实验结果

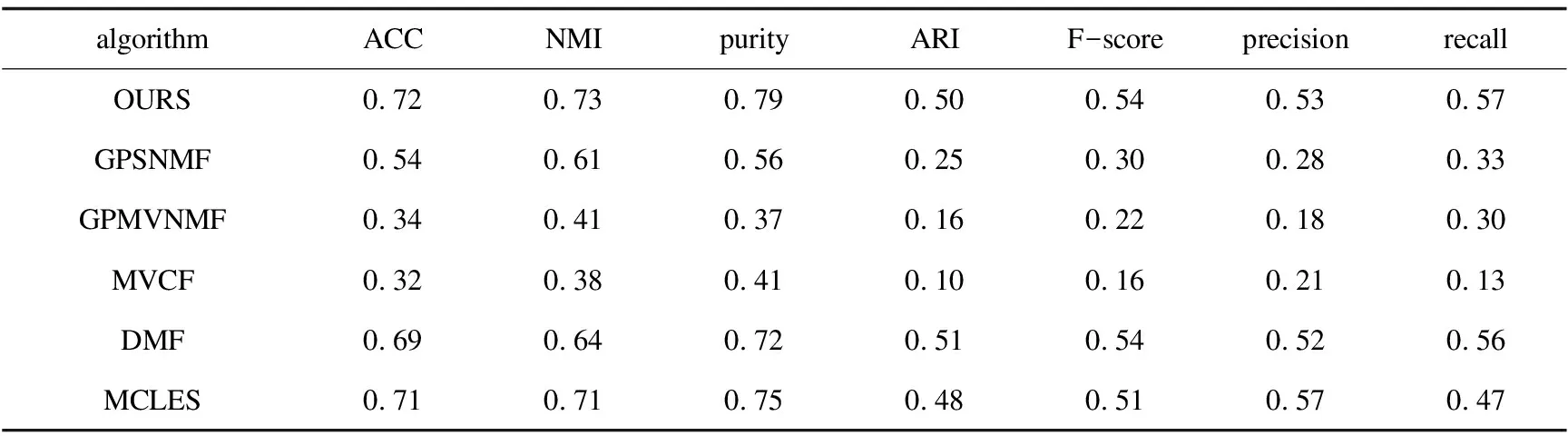
表3 Yale数据集实验结果

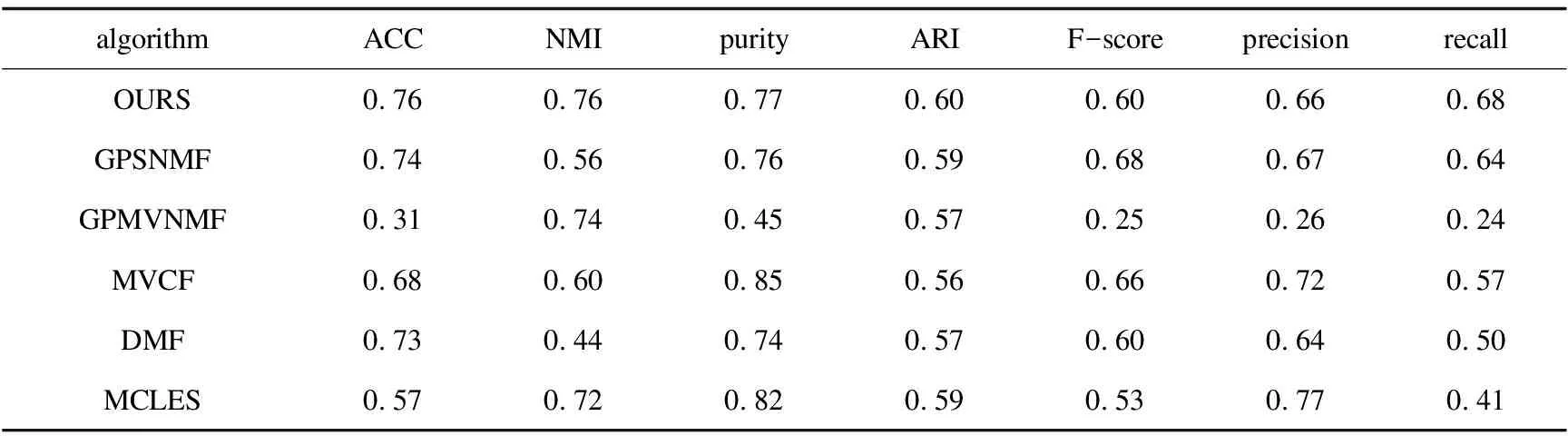
表4 3-Sources数据集实验结果

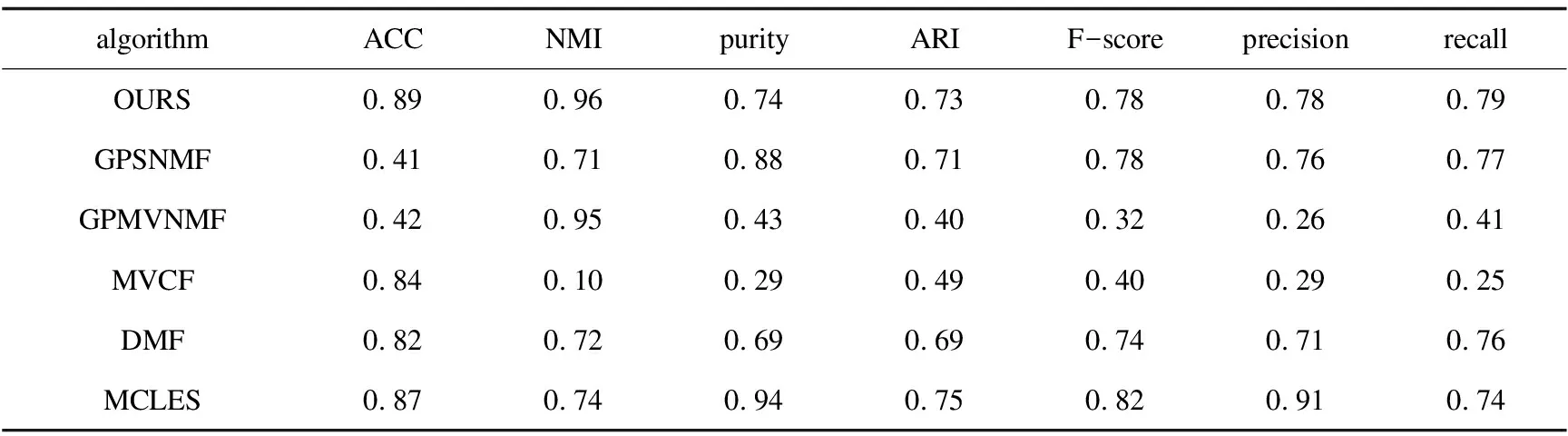
表5 BBCSport数据集实验结果

(1)针对图像数据集ORL,MSRCv1和Yale,MSRNMF相较于MVCF,GPSNMF,GPMVC和MCLES在ACC与NMI两个聚类指标上得到了显著改进,较最优算法至少提升了0.1左右,MSRNMF与MCLES在ACC与NMI两个聚类指标上相差不大;在purity,ARI,F-score,precision和recall上,MSRNMF不都是最优算法,但是相较GPMVNMF得到了明显改进,至少提升了0.2。

(2)针对文本数据集3-Sources和BBCSport,MSRNMF相较于MVCF,GPSNMF,GPMVC,DMF和MCLES,在ACC上至少提升了0.2;相较于GPSNMF和MVCF,在NMI上得到了显著改进,至少提升了0.1;在purity,ARI,F-score,precision和recall上,MSRNMF较最优算法最多相差0.2,MSRNMF较GPMVNMF得到了明显改进,提升了0.3以上。

4.4.2 古建筑数据集下的结果

以金光寺为对象,聚类数选择6和8,MSRNMF的结果如图3和图4所示。

图3 聚类数为6时金光寺聚类结果图

图4 聚类数为8时金光寺聚类结果图

从图3和图4可以看出,簇数为6,8时,MSRNMF对非负矩阵分解的目标函数添加L21范数和核范数,剔除了图像噪声,提高了古建筑多视图聚类的鲁棒性;结合MSR融合各单视图聚类结果,进一步平衡了各单视图的重要性,最终得到一个较好的聚类结果。

5 结束语

针对海量高维数据,现有多视图聚类方法很难发现数据的隐藏信息,无法平衡每个视图的重要性。针对上述问题,提出了一种基于非负矩阵分解和均方残差的子空间多视图谱聚类算法(MSRNMF)。该方法设计了一种改进的非负矩阵分解误差,提高了矩阵分解的鲁棒性和稀疏性;引入流形正则化和希尔伯特-施密特独立性准则,加强了视图内部和视图之间信息的联系和融合。以标准数据集和古建筑数据集为对象,MSRNMF与MVCF,GPSNMF,GPMVC,DMF和MCLES相比,在ACC与NMI两个聚类指标上得到了显著提升,MSRNMF产生了显著改进的结果。