集成学习方法的应用与比较

成 佩，孟 勇

（山西财经大学a.应用数学学院；b.财政与公共经济学院；c.资源型经济转型发展研究院，太原 030006）

0 引言

机器学习方法在处理复杂数据、构建高精度模型方面具有显著优势，在不同领域的研究中都得到了广泛应用[1]。在车险损失的预测中，已有很多学者利用不同的机器学习方法对车险损失进行预测[2—4]，并将预测结果与广义线性模型（Generalized Linear Models，GLM）作了比较，这些文献表明，机器学习方法中的神经网络、装袋法、梯度提升树等模型提高了对车险损失的预测精度。还有学者对比了不同机器学习方法对车险损失的预测结果。如孟生旺等（2017）[5]将支持向量机、神经网络、梯度提升树等多种机器学习方法应用于车险损失的预测中，采用均方根误差和KL 散度指标评价了各模型对累积赔款的预测效果，结果表明支持向量机和梯度提升树在不同评价指标上表现均相对优越。有学者收集了包含国内外车险数据的七个数据集，比较了五种流行的机器学习方法和广义线性模型的预测能力，发现除了神经网络之外的四种机器学习方法的预测效果均优于广义线性模型，但无法在随机森林、梯度提升树、深度神经网络三种方法中得到统一的最优预测模型。以上研究表明，在车险损失的预测中，装袋法、随机森林、梯度提升树等集成学习方法均表现出一定的优越性，但基于常用的评价指标无法比较哪种模型更适用于预测车险损失。

此外，现有文献的研究大多关注车险损失的预测精度，而缺少对影响车险损失的风险变量重要性测度的研究。张碧怡等（2019）[6]基于XGBoost和随机森林对车险风险因子重要性测度作了比较研究，表明排在前三位的重要变量基本一致。但关于影响商业车险和交强险的风险因子的重要性测度对比分析目前还未有研究。

为了探析哪一种集成学习方法对车险损失的预测更有效，本文在常用的评价模型预测水平的平均绝对误差和均方根误差的基础上，提出了综合平均误差及稳定性指标，分别用于评价不同集成学习方法的预测效果及稳定性，从而在多个预测模型中选出最优车险损失预测模型。另外，为了对比影响不同险种的重要风险变量，本文分别以商业车险和交强险累积索赔额为被解释变量建立预测模型，进而分析比较影响不同险种损失的风险变量的重要性，以期为承保公司对个体风险进行分类提供依据，以提升不同险种定价的合理性。

1 集成学习预测模型

集成学习是通过采用某种策略将多个“基学习器”组合成一个预测效果优良的“强学习器”来完成学习任务的，通常集成以后可以获得比单个“基学习器”显著优越的泛化性能。装袋法、随机森林和梯度提升树是典型的集成学习方法，决策树是最常见的“基学习器”。

下面主要介绍决策树及装袋法、随机森林和梯度提升树这三种集成学习方法建立的车险累积索赔额预测模型、生成规则及主要参数。

假设数据集D={(xi，yi)，i=1，2，…，n} 由n份保单构成，其中表示第i份保单有p个特征变量（如车价、车龄等），yi表示第i份保单的累积索赔额。

1.1 决策树（Tree）

数学模型：

其中，M表示生成的决策树有M个叶节点，分别用L1，L2，…，LM表示；为第m个叶节点Lm中所含保单的平均累积索赔额；示性函数I(xi∈Lm)表示生成的决策树对第i份保单累积索赔额的预测值。

生成规则：预测累积索赔额决策树在每次分裂生长过程中，从所有特征变量中任意选择第j个特征变量x(j)及临界值s，将当前节点分成两个对应子节点，分别为R1(j，，进一步计算分裂后两个子节点离差平方和之和，即：

其中，=ave(yi|(xi，yi)∈R1(j，s))表示R1(j，s)中所含保单的平均累积索赔额，=ave(yi|(xi，yi)∈R2(j，s))表示R2(j，s)中所含保单的平均累积索赔额。遍历所有特征变量和临界值，选择使式（2）达到最小的特征变量和临界值作为最优分裂变量和最优临界值，对当前节点进行分裂。如此递归，直至满足条件才停止分裂，得到叶节点，这样就生成了一棵决策树。

1.2 装袋法（Bootstrap aggregating，简记为Bagging）

数学模型：

其中，B表示最优决策树的数量；表示第b棵最优决策树对第i份保单累积索赔额的预测结果；表示Bagging 模型对第i份保单累积索赔额的预测结果。

Bagging 模型中B棵最优决策树的生成规则：采用自助抽样法对数据集D={(xi，yi)，i=1，2，…，n}进行有放回的再抽样，得到B个自助样本，第b（b=1，2，…，B）个自助样本可以表示为，每个自助样本都包含n份保单。第b棵最优决策树是基于第b个自助样本D*b中的n份保单按模型（1）自然形成的，其中每个内部节点分裂时，是从所有特征变量及临界值中选择使式（2）最小的变量和临界值，无须剪枝。

Bagging模型的主要参数包含决策树的数量（B）、叶节点最小样本点（nodesize）。

与单棵决策树相比，Bagging 的优点是降低了测试误差。Bagging 将多棵决策树的预测结果进行平均，降低了估计量的方差。每棵树尽情生长不需要剪枝，降低了每棵决策树的偏差。

1.3 随机森林（Random Forest）

数学模型：

其中，B表示最优决策树的数量；表示第b棵最优决策树对第i份保单累积索赔额的预测结果；表示Random Forest对第i份保单累积索赔额的预测结果。

Random Forest 模型中B棵最优决策树的生成规则：采用自助抽样法得到B个自助样本。与Bagging模型不同的是，在基于第b个自助样本n}按模型（1）形成第b棵决策树的过程中，每个内部节点依据式（2）最小原则进行分裂时，是从所有特征变量中随机选取一部分变量作为分裂候选特征变量。

Random Forest参数有决策树的数量（B）、叶节点最小样本点（nodesize）、备选特征变量个数（mtry）。

Random Forest 与Bagging 数学模型相似，但为了降低最优决策树之间的相关性，每棵最优决策树的生成过程有所不同。例如，如果车价是所有特征变量中影响累积索赔额的最主要变量，那么Bagging 模型中大多数树都会在最初节点分裂中选择车价作为最优分裂变量，从而导致Bagging 模型中决策树之间存在较高的相关性。Random Forest在不同节点仅采用随机选取的部分特征变量作为候选分裂变量，从而可以保证至少有一些树在最初节点分裂中选择了除车价之外的其他变量作为最优分裂变量，降低了B棵最优决策树之间的相关性，进而有效降低了估计量方差。另外，由于在每个节点分裂时未使用全部信息，因此会增大偏差。

1.4 梯度提升树（Gradient Boosting Tree，简记为GBT）

数学模型：

GBT生成过程如下：

（1）利用所有保单构成的数据集D={(xi，yi)，i=1，2，…，n}生成一棵仅有一个叶节点的决策树：

对任意xi（i=1，2，…，n），有：

（2）第b（b=1，2，…，B）棵决策树的生成迭代过程如下：

利用损失函数沿负梯度方向下降最快的原理，计算损失函数的负梯度在当前模型的值=yi-fb-1(xi)（i=1，2， …，n），即当前模型对第i份保单累积索赔额的预测误差；由第i份保单xi及其对应的误差构成新数据集在Db下利用模型（1）拟合第b棵决策树f̂b(tree)(·)，其中每个内部节点依据式（2）最小原则选择分裂变量和临界值进行分裂。

以学习率ηb为步长更新当前模型fb(xi)=fb-1(xi)+ηb，进入上述迭代过程。直至第B棵决策树生成，迭代停止，这就形成了GBT模型。

GBT模型参数包括决策树的数量（B）、树的交互深度（depth）、叶节点最小样本数（nodesize）、学习率（shrinkage）。

GBT的基本思想是通过拟合之前决策树的残差，使以后生成的决策树修正之前决策树的错误。与Bagging 和Random Forest 相比，GBT 模型中的B棵决策树是依次而种，相对位置不能随意更改。由于每棵树纠正了上一棵树的错误，因此可以有效降低偏差。

从上述四种机器学习方法的数学模型可以看出，机器学习方法无须设定模型的函数形式，且可以从车险数据中自动识别变量存在的交互效应及非线性关系，因此更具灵活性。另外，从模型的作用机制可以分析出，Bagging、Random Forest、GBT 这三种集成学习的预测效果优于单棵决策树，但从理论上无法判断哪种方法具有绝对的优势。

2 集成学习预测模型的评价

常用的评价不同集成学习方法预测性能的指标主要有平均绝对误差、均方误差、均方根误差，除此之外，本文还提出了综合平均误差和度量模型稳定性的σ2。

（1）平均绝对误差（Mean Absolute Error，MAE）

（2）均方误差（Mean Square Error，MSE）

（3）均方根误差（Root Mean Square Error，RMSE）

以上是目前通常采用的评价预测模型的指标，与MSE相比，MAE和RMSE的计算结果与目标变量的量纲保持一致，因此更常用，但两者又存在一些缺陷。MAE选择的最优模型对离群点不敏感，RMSE选择的最优模型则是以牺牲正常点的拟合效果为代价，对离群点容易产生过拟合。本文以车险损失数据为实证分析对象，但车险损失数据中仅有少数数据属于离群点，绝大多数车险损失为0，数据具有极不平衡的特点。若采用某种单一指标评价车险损失的预测模型，则可能导致预测结果偏大或偏小。针对研究问题的特殊性及MAE、RMSE 两个指标的特点，本文构造了一个新指标，即综合平均误差。

（4）综合平均误差（Composite Mean Error，CME）

该指标是MAE 和RMSE 的等权重平均值，对两者在离群点和正常点的惩罚权重做了平滑处理。采用CME评价预测模型，既考虑了异常损失带来的重要风险影响，又不会产生对离群点过拟合的结果，使得预测结果更准确。因此本文采用该指标对比不同机器学习方法在车险损失预测方面的效果。

（5）模型稳定性σ2

考虑到在集成学习方法中，Bagging、Random Forest 及GBT均是以决策树作为“基学习器”，其中决策树的生长存在分裂方式上的不唯一性，即在最优参数下，得到的最优模型具有一定的随机性。因此，需要提出一个指标来衡量最优模型的波动性水平。为了讨论这三种机器学习算法的稳定性，本文提出了σ2指标。

3 数据介绍及模型最优参数

3.1 数据介绍

本文选取了国内某保险公司2018—2020年的商业车险和交强险损失数据，数据的分布情况见表1。

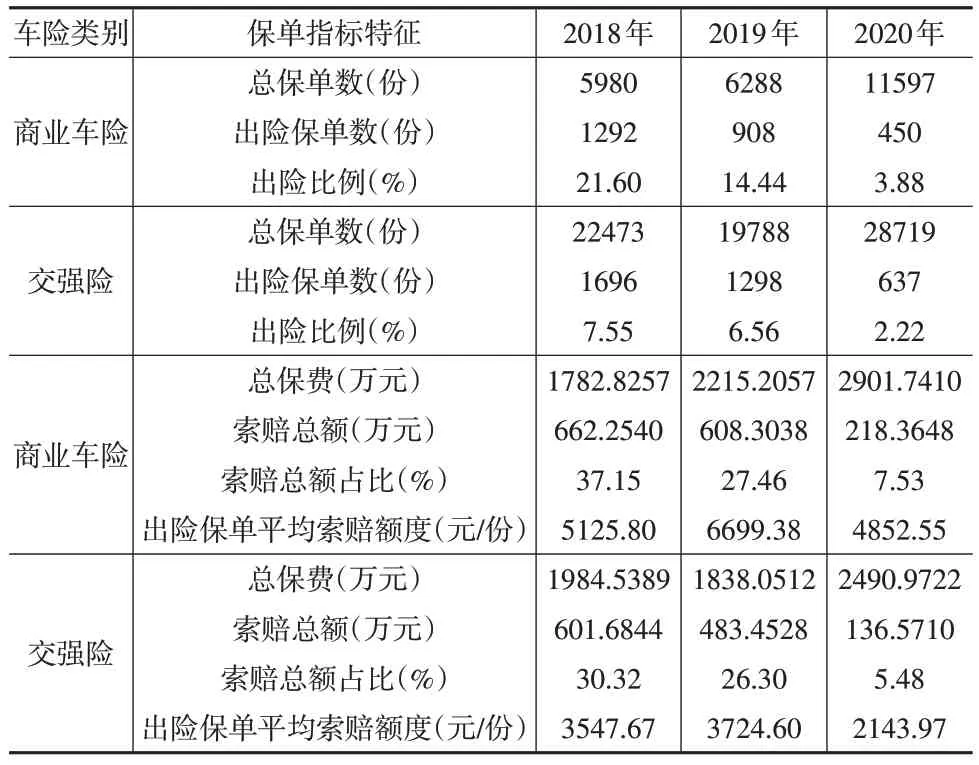
表1 保单在各保险年度出险的数据分布

从表1中不难发现，2018—2020年商业车险的出险比例均高于交强险，说明商业车险发生索赔的可能性要高于交强险。对于出险的保单，商业车险的平均索赔强度要高于交强险，这主要是因为商业车险保障范围及保障强度都大于交强险。由此可提出假设，风险变量对不同类别车险未来累积索赔额的影响程度不一样。因此，本文分别对商业车险和交强险进行预测建模，探索在不同保险类别中风险变量对累积索赔额的影响。

数据集共有9 个变量，其中被解释变量是累积索赔额，解释变量有8个，具体如下页表2所示。

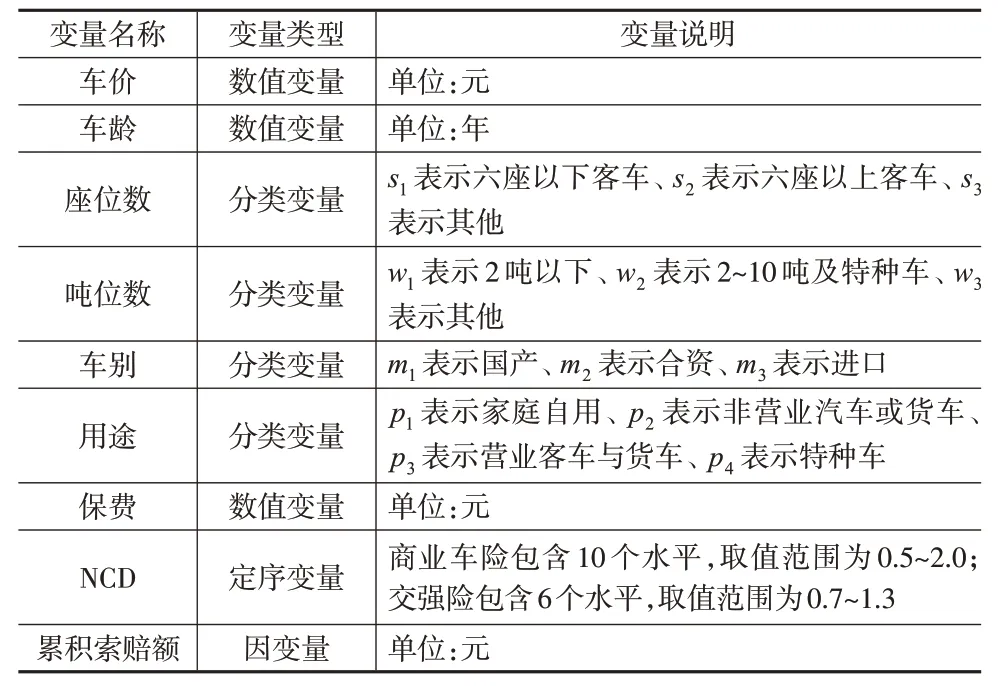
表2 数据集的变量列表

3.2 数据预处理及数据集划分

从表1中可以看出，数据集中出险保单与未出险保单的比例严重失衡，说明样本数据是不平衡的。在实际应用中，针对不平衡数据进行调整的方法主要有两种：一种是欠抽样，减少未出险保单的数量，使之与出险保单数量相当，两者合并得到一个较为平衡的样本；另一种是过抽样，通过增加出险保单的比例来实现样本平衡。由于本文选取的数据集规模并不是很大，因此采用过抽样的方法调整不平衡，避免因删除一部分数据产生信息损失问题。

将处理后的数据集按7：3 划分为训练集和测试集。利用训练集训练模型，并基于交叉验证调节最优参数，在测试集上检验最优参数下模型的预测水平。

3.3 模型最优参数选择

由于Bagging、Random Forest 及GBT 模型中含有多个参数，因此为了得到最优拟合模型，需要对各模型的参数进行网格搜索，并通过交叉验证得到最优参数。表3显示了参数调优的选择范围及得到的最优参数。表3 中最后一列是在2018年商业车险数据集上得到的各模型对应参数的最优取值。

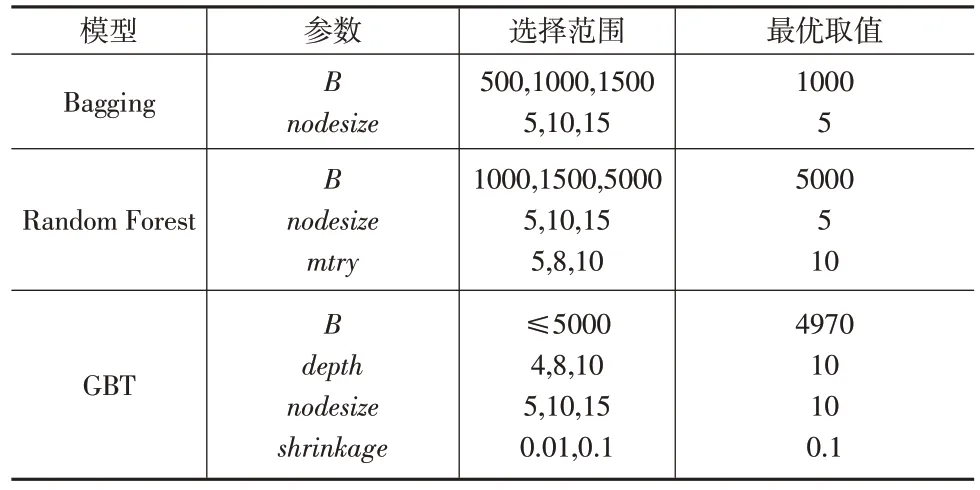
表3 参数调优的选择范围及最优参数

4 实证结果

本文采用广义线性模型、决策树、装袋法、随机森林及梯度提升树分别对2018—2020年商业车险和交强险单位风险的累积索赔额进行预测建模。

4.1 预测效果比较

在比较不同模型的预测效果时，采用了常用的MSE、RMSE和MAE，以及本文构造的CME和σ2，这些指标的取值越小，说明模型预测效果越好。

表4 至表6 为各模型在2018—2020 年商业车险数据集上的预测结果。可以看出，在商业车险累积索赔额的预测模型中，四种机器学习方法的预测效果均表现得更好，其中单棵决策树的预测效果稍差一些。在三种集成学习方法中，以MSE 和RMSE 作为评价指标，2018—2019 年数据集上GBT 模型预测效果最好，2020 年数据集上Random Forest 模型预测效果最好；以MAE 作为评价指标，Bagging模型表现最好。

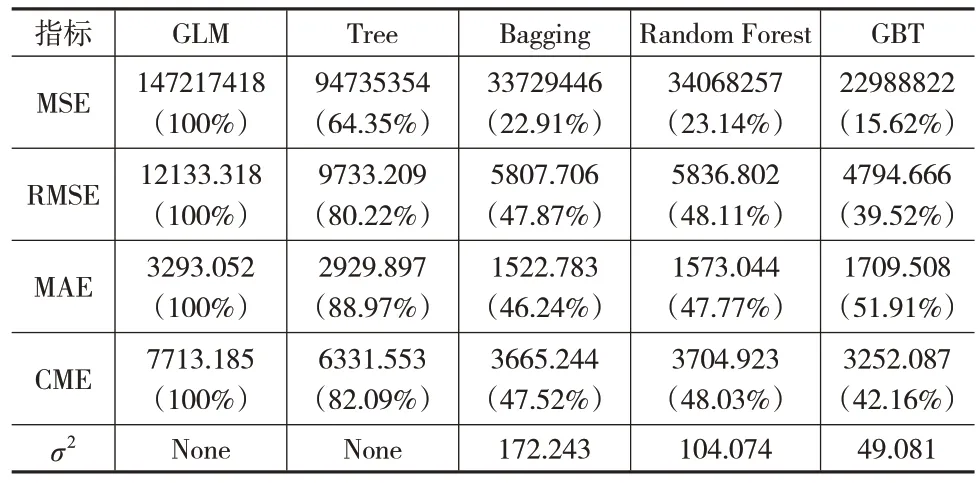
表4 2018年商业车险各模型预测结果对比

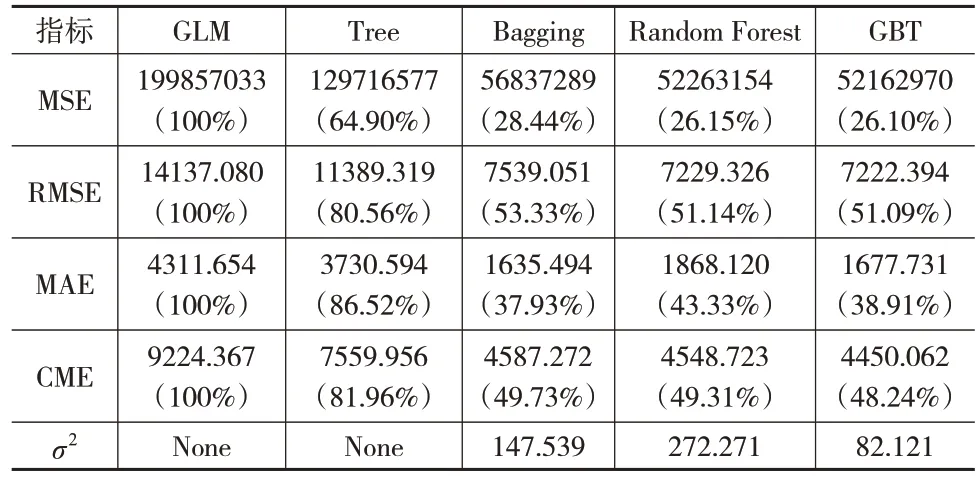
表5 2019年商业车险各模型预测结果对比

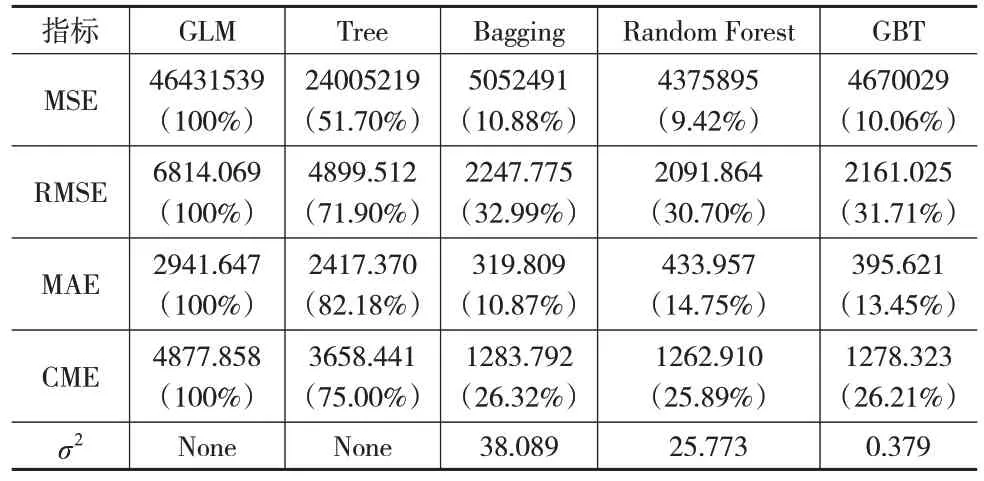
表6 2020年商业车险各模型预测结果对比

图1 展示了采用CME 指标对比不同模型对商业车险累积索赔额的预测效果。直方图的高度是以GLM模型的CME 为基准，不同模型与之相比预测效果提升的程度。高度越高，提升的程度越大，说明预测效果越好。

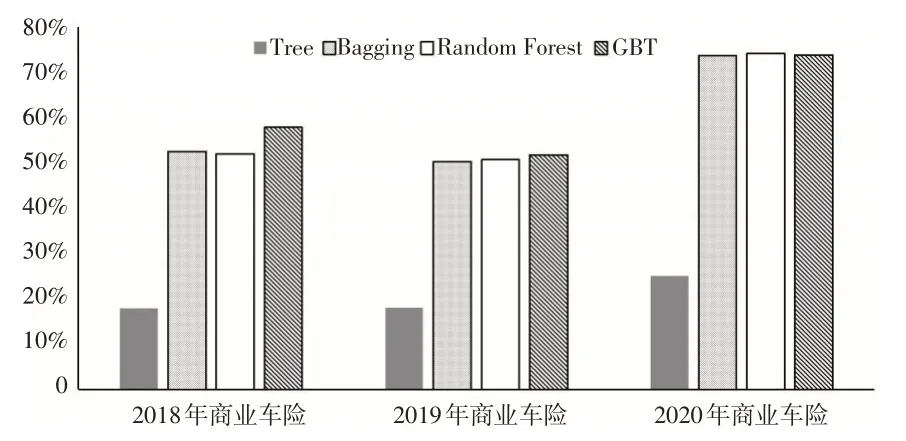
图1 商业车险中机器学习与GLM关于CME指标的比较

将CME 作为评价指标，结合图1 可以看出，机器学习方法的预测效果比GLM 模型提高了不少，其中三种集成学习方法的提高幅度都超过了50%。在2018年数据集上GBT模型预测效果最好，相比另外两种集成学习方法优越性较突出，在2019 年和2020 年数据集上，分别是GBT 和Random Forest模型表现最优，但三种集成学习方法的预测效果相差并不明显；将三种集成学习方法3年数据集上的CME指标进行平均，发现GBT模型的对应值最小，即GBT模型的平均预测效果最好。对比三种集成学习方法的稳定性，表4至表6中一致认为GBT模型的预测波动方差最小、最稳定。因此与其他模型相比，GBT 模型对商业车险累积索赔额的预测效果要更好。

表7 至表9 比较了各模型在2018—2020 年交强险数据集上的预测效果。

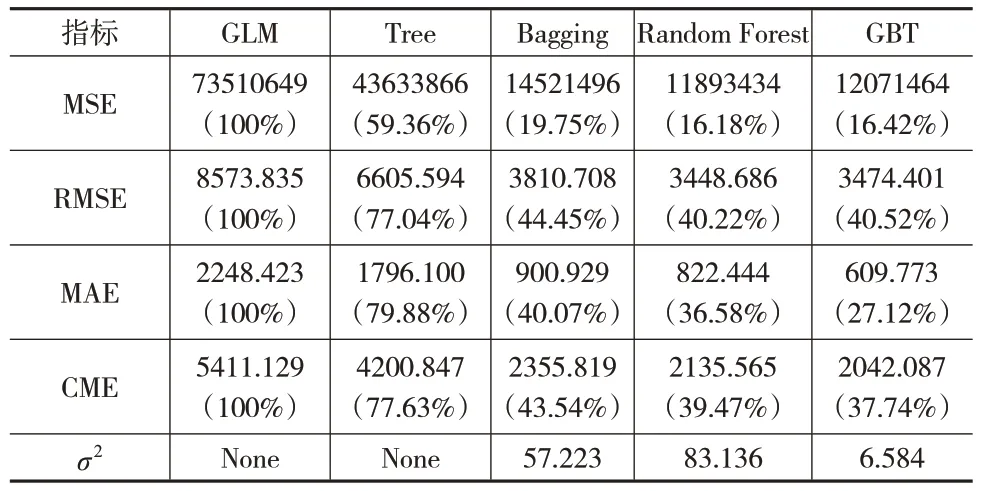
表7 2018年交强险各模型预测结果对比

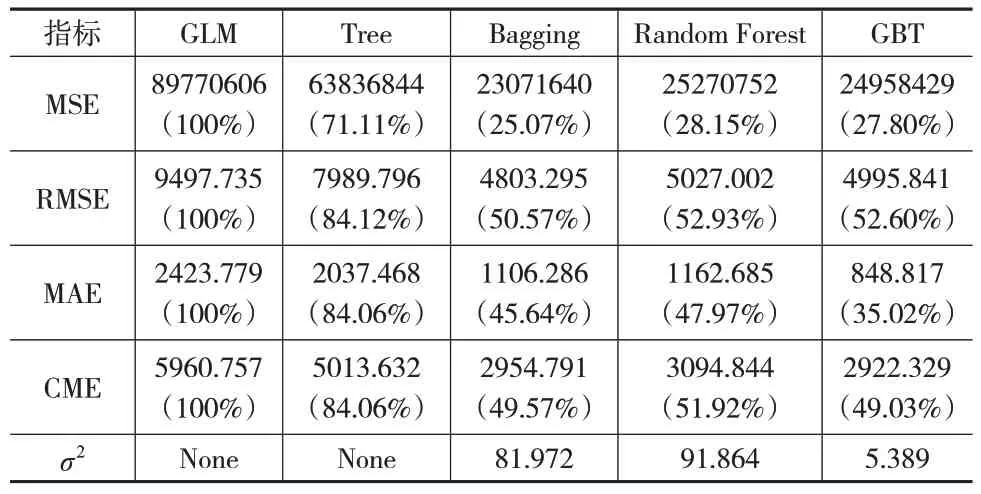
表8 2019年交强险各模型预测结果对比

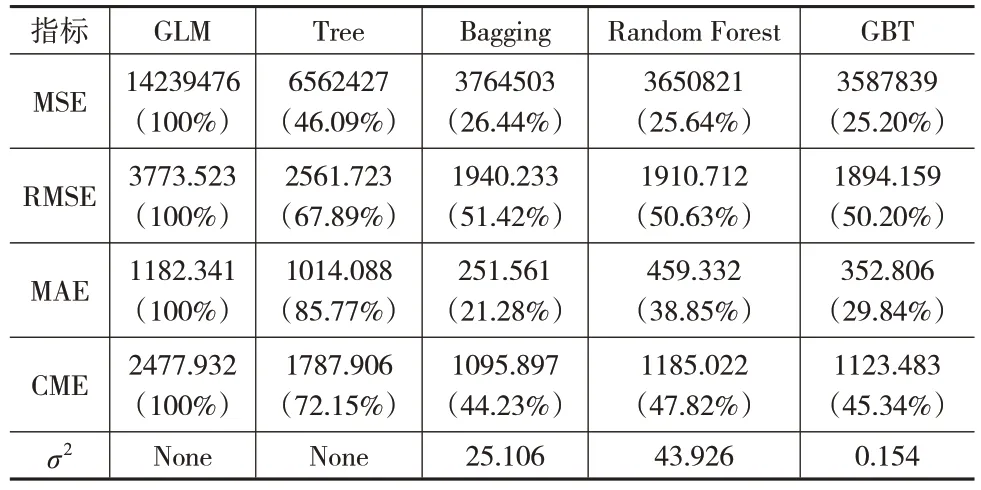
表9 2020年交强险各模型预测结果对比

可以看出，集成学习方法预测效果要优于单棵决策树和GLM 模型。三种集成学习方法中，以MSE 和RMSE 作为评价指标，在2018—2020 年数据集上预测效果最好的模型分别是Random Forest、Bagging、GBT。以MAE作为评价指标，在2018—2019年数据集上GBT模型表现最好，在2020年数据集上Bagging模型表现更好。

图2 展示了采用CME 指标评价不同机器学习方法对交强险累积索赔额的预测效果，直方图的高度说明同图1。

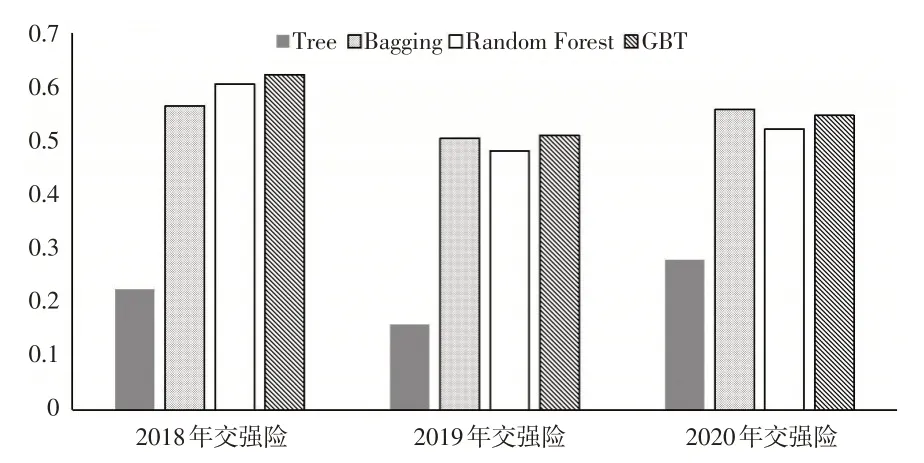
图2 交强险中机器学习与GLM关于CME指标的比较

将CME 作为评价指标，结合图2 可以看出，在2018—2019 年数据集上GBT 模型预测效果最优，尤其是在2018年数据集上其与Bagging 模型相比优越性较突出，在2020年数据集上Bagging 模型预测效果更优，但GBT 模型的预测效果和Bagging 模型的差距并不明显；将三种集成学习方法3年数据集上的CME指标进行平均，发现GBT模型的对应值最小，即GBT 模型的平均预测效果最好。对比三种集成学习方法的稳定性，表7至表9一致认为GBT模型的波动方差最小、最稳定。因此整体上GBT 模型对交强险累积索赔额的预测效果最好。

4.2 不同险种的变量重要性排序

集成学习方法在预测不同险种的累积索赔额时，虽然无法像GLM 模型一样给出拟合模型的显性函数表达式，但可以度量不同风险变量对累积索赔额的影响程度。通过在所有数据集上比较CME 和σ2两个指标可以发现，GBT 模型的预测效果更好。因此本文基于GBT 模型的预测结果，分别在商业车险和交强险两类不同险种下，讨论各风险变量的相对重要性。在R 中，GBT 模型通过summary（）可以得到各个风险变量相对影响的百分比，取值越大，说明该变量对累积索赔额的影响效应越大。。

通过图3可以看出，在2018—2020年商业车险数据集上，一致认为排在前三位的重要变量分别是保费、车价、车龄。其中，保费和车价对商业车险累积索赔额的影响程度要明显强于其他变量，车龄和NCD有一定的影响作用，其他变量的影响效应相对微弱。

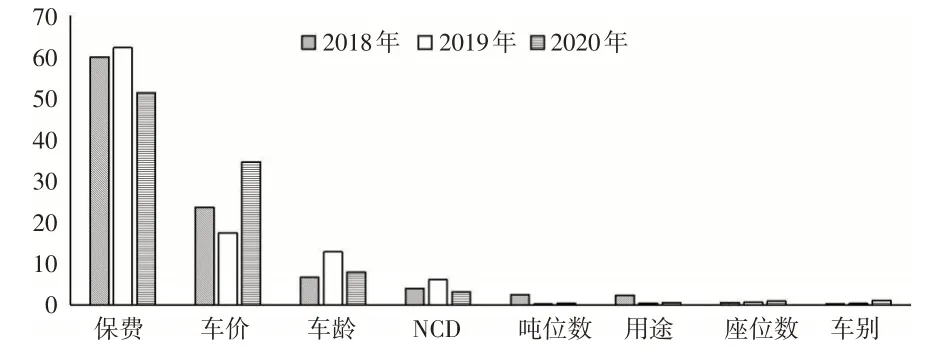
图3 影响商业车险累积索赔额的变量重要性排序

下页图4 描述了影响交强险保单累积索赔额的变量重要性排序。在2018—2019 年数据集上，一致认为排在前三位的重要变量分别是车价、车龄、保费，在剩余变量中，NCD的影响效应相对较强，其他变量的影响不明显。在2020年数据集上，变量重要性顺序发生了很大变化，排在前三位的变量分别是车价、车别、车龄，其中车价的影响程度较前两年有所上升，车龄的影响效应较前两年则有所下降。

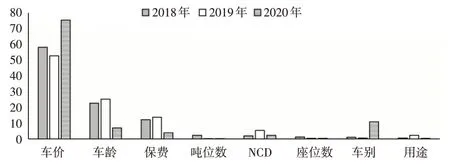
图4 影响交强险累积索赔额的变量重要性测度

下页图5 至图7 分别比较了在2018—2020 年数据集上，同一风险变量对商业车险和交强险这两个不同险种的重要性。从图5至图7可以看出，同一风险变量对不同险种累积索赔额的影响效应是不同的，尤其是排序靠前的风险变量对不同险种累积索赔额的影响效应差异性很大。其中，保费对商业车险累积索赔额的影响明显强于交强险；车价对交强险累积索赔额的影响显著高于商业车险；车龄对交强险累积索赔额的影响更大，但对两者影响的差距随时间推移逐渐缩小；NCD对商业车险累积索赔额的影响要大于交强险；车别对两种保险累积索赔额的影响随时间推移差距逐渐扩大。

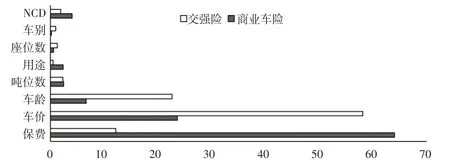
图5 风险变量对2018年商业车险和交强险累积索赔额的影响效应比较

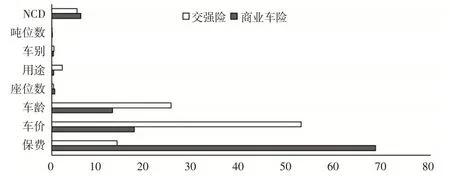
图6 风险变量对2019年商业车险和交强险累积索赔额的影响效应比较

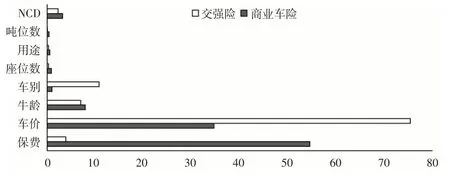
图7 风险变量对2020年商业车险和交强险累积索赔额的影响效应比较

5 结论

本文通过使用2018—2020年商业车险和交强险数据集，基于广义线性模型、决策树、装袋法、随机森林及梯度提升树分别对商业车险和交强险单位风险的累积索赔额进行建模预测，发现在三种集成学习方法中，梯度提升树适合在车险领域建立损失预测模型，其不仅能提高对未来累积索赔额的预测精度，还具有较高的稳定性。进一步利用该模型对比了影响商业车险和交强险累积索赔额的重要风险变量，发现不同险种的重要风险变量排序不同，且排序靠前的重要风险变量对两种险种未来累积索赔额的影响效应有明显差异，对改善不同险种的保费厘定结构具有重要的应用价值。