基于LSTM的政策效应预测模型及其应用

李树娴，张晓骏，胡成雨

（1.武汉工商学院 经济与外语学院，武汉 430065；2.中南财经政法大学 统计与数学学院，武汉 430073）

0 引言

作为政策科学的重要组成部分，政策评估成为衡量政策效能的重要手段。比较分析政策效应可以实现精准的宏观经济调控。目前，已有许多文献研究政策效应评估方法的评估精度。双重差分法（DID）和合成控制法（SCM）因其简便易用的特点，被应用于多种政策评估。周朝波和覃云（2020）[1]运用DID和稳健性检验研究碳交易试点政策对中国低碳经济转型的影响；柳天恩等（2019）[2]使用DID 评估了国家级新区设立政策对地区经济发展的影响；武剑和谢伟（2019）[3]运用SCM对上海、广东、福建、天津自由贸易试验区政策的经济效益进行了评估；丛树海和黄维盛（2022）[4]使用多事件合成控制法评估了重大疫情冲击对财政可持续性的影响。其中，DID 通过赋予对照组等权重，对处理组信息与共同变化趋势的对照组信息作差分来计算平均处理效应，但共同趋势假定太过严苛；SCM 通过赋予对照组不等权重来构造与处理组个体相似的单元，要求权重非负且无法处理具有大量协变量的情况，回归控制法（HCW）放松了权重非负要求，但当对照组个体数量太多时AIC信息准则会失效。

随着信息化时代的到来，具有精准样本匹配和优良预测性能的机器学习方法[5,6]逐渐引起学界的关注，机器学习模型能够通过对复杂关系建模实现反事实推断的精准预测，从传统计量经济方法到机器学习方法的应用已经成为重要的发展趋势。钱佳丽和黄先军（2022）[7]使用VAR 模型分析了货币供给政策、物价水平和外贸进出口之间的变动关系；张铭茗（2021）[8]使用SVAR 模型和格兰杰因果检验分析了人民币汇率政策与进出口贸易增额之间的关系。沈艳等（2022）[9]对比了传统计量方法和机器学习方法在面板数据下的效应识别，提出了基于面板大数据的因果效应估计和推断方法建议。钱浩祺等（2021）[10]分析了因果推断的主流框架和内在联系特征，提出了将机器学习融入样本匹配和反事实预测，以增强因果效应识别能力。现有的政策评估方法改进主要聚焦于处理组、对照的多样性、信息的有效性等[11,12]，为了提高机器学习反事实预测精度，实现更好的政策效应评估，本文融合了深度学习技术和反事实因果推断，提出一种基于长短期记忆神经网络（LSTM）的政策效应预测方法，将深度学习方法应用到因果效应识别的样本匹配，同时发挥模型精准的预测能力，以湖北省政府优惠贷款利率政策为例，测定其对湖北省外贸经济的效益影响。

本文主要从两个方面进行了拓展：（1）结合深度学习技术，利用LSTM神经网络的非线性拟合能力测算处理组的反事实预测结果，检验其在政策处理效应中的应用。（2）结合SCM 方法的优良特性，提出基于合成控制的LASSO回归方法，通过机器学习中的交叉检验来确定最佳参数以及最优模型。

1 研究设计

1.1 SCM-LASSO回归

1.1.1 LASSO

LASSO是筛选模型中重要协变量的常用方法，通过在最小二乘法中引入惩罚项来实现变量选择和参数估计[13]，通过构造惩罚函数可以将变量的系数进行压缩并使某些回归项系数趋近于0，从而达到降维和变量筛选的目的。考虑线性模型的参数估计：

其中，y是n×1的观测向量，X为n×p的设计矩阵，β是p×1的未知参数向量，ϵ为随机误差项，σ2为误差的方差。利用最小二乘法，使得误差向量ϵ=y-Xβ尽可能小，即：

达到最小，Lasso回归在目标函数Q(β)后添加L1范数得到Q(β)'：

其中，惩罚项系数λ可以用来控制变量筛选的系数程度。最小化目标函数即可得到筛选后的变量和回归项系数。L1 正则项使得原先处于零附近的参数β往零移动，使得部分参数为零，降低模型的复杂度，从而防止过拟合，提高模型的泛化能力。LASSO 的应用可以在进行参数估计的同时实现变量的选择，较好地解决回归分析中的多重共线性问题，同时得到较好的解释结果。

1.1.2 SCM合成控制法

合成控制法是多数文献常用的政策评估模型之一，该方法相比传统计量模型的优势在于防止了人为选择对照组的主观误差，构造的对照组较为客观和透明。SCM的思想是选择一组与处理组具有相似因素特征、但在过去一段时间内未受到政策干预的对照组，通过对选取的对照组进行线性组合，构造一个近似处理组的合成控制组，用以衡量控制组未受到干预时的变量值。假设处理组受政策干预前各预测变量值为向量x1，对照组相应的预测变量值为矩阵x0，则有：

使得加权构造的对照组变量值与控制组变量值近似,找出最佳权值矩阵ω，权重参数的求解为具有约束的加权平方和最小化问题：

其中，V是K×K对角矩阵，J为对照组数量。求出权重矩阵ω即可得到构造的处理组，与处理组变量值作差即可得到平均处理效应，进而估计政策效应。

1.1.3 SCM-LASSO回归

本文将LASSO 变量筛选思想引入SCM 合成控制法中，对政策干预前的对照组个体进行变量筛选，拟合对照组与处理组之间的变量关系，预测政策干预后的处理组变量值。具体设计思路为：假设共有N=D+1 个个体、T个时期的面板数据，设Cit=1 表示个体i在t时期受到政策约束，Cit=0 表示未受到约束；及表示个体i在t时期受到政策约束和未受到政策约束的潜在结果，Yit表示个体i在t时期的实际观测数据，根据事实结果，有：

假设T0为政策干预时点，则对于处理组个体来说，有：

对于D个对照组个体有：

本文以对照组D个个体信息为基础，利用SCM 思想为每个个体赋予不等权重，结合LASSO 回归系数惩罚项（λ为调节系数）对对照组个体进行控制筛选，从而构造与处理组较为相似的单元信息Yi0t（t=T0+1，…，T），并以此作为处理组的反事实结果。由此即可得出政策约束对处理组的处理效应τ1t以及平均处理效应

1.2 LSTM长短期记忆神经网络

LSTM 长短期记忆神经网络是一种循环递归神经网络，所有层共享相同的权值，通过引入记忆细胞特殊类神经单元来控制长距离信息的输入，弥补了普通神经网络无法依赖长时信息的缺陷，该记忆单元在下一个时间步长将拥有一个权值并联接到自身，拷贝自身状态的真实值和累积的外部信号，因此更加适用于时间序列数据预测。LSTM单个神经细胞主要包含四层结构：遗忘门、输入门、输出门和一个单元状态[14]。通过控制门来对细胞单元进行信息的添加和删除，通常由一个sigmoid神经网络层（见图1）和一个成对乘法操作组成，sigmoid 层将学习到的特征信息压缩到0至1范围内，决定了当前门单元通过信息的多少。通过输入当前时刻的网络输入值xt、上一时刻网络的输出值ht-1和上一时刻的单元状态Ct-1来得到当前时刻网络的输出值ht和单元状态Ct。具体结构如下页图2所示。

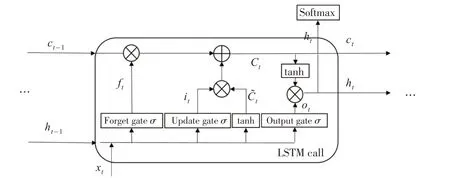
图1 LSTM单元细胞结构

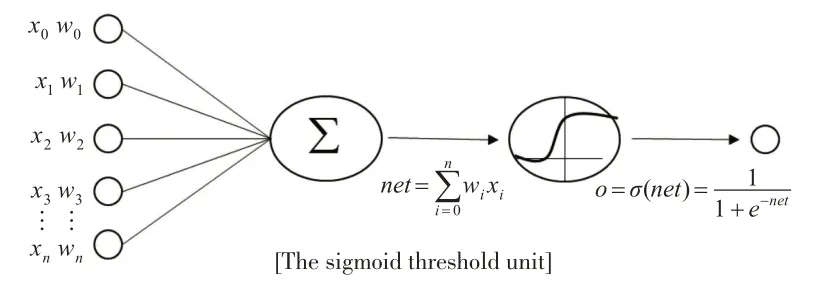
图2 sigmoid(σ)层函数结构

门结构的主要计算公式为：

其中，Wf、Wi、WC和WO分别表示遗忘门、输入门、输出门和计算单元状态的权重矩阵，bf、bi、bc、bo表示对应门的偏置项，ft表示上一时刻单元状态通过率，it表示输入门更新值，Ct表示当前状态的候选值，ht表示当前网络的输出值。遗忘门根据网络上一时刻输出值ht-1和当前输入值xt来决定上一时刻单元状态Ct-1有多少信息保留到当前状态，0 表示全部遗忘，1 表示全部保留；输入门通过sigmoid层函数与tanh层函数产生网络更新值与状态候选值Ct,组合决定当前网络输入值xt有哪些保存到当前单元状态Ct，即给当前细胞添加多少新的信息，通过遗忘门和输入门可以对当前细胞信息进行交替更新和保留；输出门通过控制单元状态ht-1和当前输入值xt决定LSTM网络的当前输出值ht[14,15]。Sigmoid层计算得到输出门的判断条件，tanh 层得到当前细胞状态的向量值，两层相乘即可得到当前单元的输出。模型通过误差项的反向传播及时调整各门的权重矩阵，最终达到设定好的迭代次数或者最优值才停止学习。本文利用LSTM 的负责建模能力，将其应用到因果推断的样本匹配和反事实推断预测，从而得到更为精准的平均处理效应预测，以更好地评估政策方案带来的效应。

1.3 评价指标

为了验证所提方法的有效性和鲁棒性，本文使用误差指标来计算模型预测值与实际观测值之间的差距，以此度量不同模型的预测精确度，包括相对误差、均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）。相对误差可以用预测值与实际值的差值，再除以实际值计算得到，用以衡量单个预测目标的精准度。均方误差（MSE）用于评估模型预测值与实际观测值之间差异的平均大小，数值与原始观测值的单位的平方相同，通过计算预测值与实际观测值之间差异的平方的平均值得到，容易理解，但是受异常值影响较大。均方误差（MSE）的计算公式如下：

RMSE是在MSE的基础上计算平方根，数值与原始观测值的单位相同，可以更好地衡量模型的预测精度，但同样易受极端值影响，对于较大的误差单元，权重较高。均方根误差（RMSE）的计算公式如下：

平均绝对误差受极值影响较小，用于衡量预测值与真实值之间的平均绝对差值，但未考虑差异的平方，没有对差异值进行放大。平均绝对误差（MAE）的计算公式如下：

四个误差指标值越小说明模型的预测效果越好。

1.4 数据来源

本文所用数据来源于中国统计数据应用支持系统提供的湖北省2008 年1 月至2021 年10 月的（境内目的地货源地）外贸进出口总额数据。由于2020年1月至2月中国各省份受新冠肺炎疫情影响，进出口总额数据存在缺失，因此本文采用二期移动平均法对缺失值进行补充，并进行标准化处理。本文利用处理后的数据进行建模，由于《湖北省进出口政策性优惠利率贷款贴息实施方案》的发布时点为2018年3月，故本文以2008年1月至2017年2月的数据集训练模型，以2017年3月至2018年2月的数据集评估模型。

2 实例验证

本文使用SCM-LASSO 回归和ANN 人工神经网络来对比验证LSTM模型的预测精度和鲁棒性。最后，以湖北省政府贷款利率优惠政策为例，检验LSTM模型在政策效应预测中的有效性。

2.1 模型预测对比分析

2.1.1 基于LSTM的模型预测

使用LSTM 神经网络对湖北省外贸进出口总额数据进行拟合，以2008年1月至2017年2月外贸进出口总额数据为训练集进行模型拟合，以2017年3月至2018年2月数据作为测试集进行预测和评估。采用三步滑窗方式[15]，以前三期历史数据作为解释变量，以后一期数据作为被解释变量构造滑动窗口，初始化隐藏层单元个数并进行参数调优，设置隐藏层神经单元个数为1，逐步递增以进行参数调优，以判定系数R2作为准则，筛选出最佳神经元单元个数为3，设置模型学习迭代次数为100，留一比率为0.1。得到模型拟合结果如图3所示。

图3 LSTM神经网络预测结果

图3中的竖虚线为训练集与测试集的分割线，以时间点2017年3月为分割点，将2008年1月至2017年2月的数据划分为训练集，2017年3月至2018年2月的数据划分为测试集，即虚线之前为训练集，虚线之后为测试集。由图3可以看出，在训练集数据上，LSTM可以很好地拟合数据的水平趋势和垂直波动，预测值与实际值变化趋势一致。LSTM 模型在训练集前期拟合效果略有不足，存在较大的波动误差，与实际值相比略微滞后，但在后期拟合效果较好，与实际值几乎重合。这是由于LSTM具有长距离信息记忆的特性，模型可以选择性地保留上一时刻单元信息和当前输入数据信息，输出当前的最佳拟合值，而后期可利用时刻数据信息较前期更多，因此拟合效果更优，输出值更精准。此外，还可以发现，在测试集数据上，LSTM精准拟合了数据变化趋势，拟合偏差也较小，输出测试集上2017 年3 月至12 月的10 期预测数值，表1 整理了测试集上的模型预测结果。由表1 可以看出，LSTM 方法预测的绝对误差和相对误差较小，模型预测的均方误差为1.36，平方绝对误差为1.28，说明模型预测误差保持在较小的范围之内，模型拟合效果较好。

2.1.2 模型对比

为了检验LSTM的预测精度，本文将LASSO惩罚项引入SCM 合成控制法中，筛选最佳对照组个体来构造处理组信息，构造SCM-LASSO 线性模型来对比预测平均处理效应，同时使用ANN人工神经网络作为对比模型，对训练集上的数值进行拟合，并与先前建立的LSTM神经网络进行比较。使用网格搜索算法遍历模型参数，选取LSTM和ANN 人工神经网络的最佳参数，同时利用机器学习交叉验证算法，对模型进行20折交叉验证，使用坐标轴下降法计算调节系数α的正则化路径，以确定方程均方误差随α数值的变化，从而挑选出LASSO 回归方程均方误差最小的α系数。计算log(α)与回归方程MSE 的变化关系，发现随着α的增加，方程的均方误差呈逐渐上升趋势，最小均方误差对应的log(α) 值为-0.2142，即α最佳数值为0.6106。最终得到各模型的超参数设置见表2。

在测试集上检验SCM-LASSO、ANN 人工神经网络和LSTM 不同模型的预测效果，发现三种模型均可以很好地拟合长期趋势，其中SCM-LASSO 的水平波动较大，LSTM模型在训练集上的拟合效果较ANN 人工神经网络略差，但是在测试集未知数据上表现较好，说明LSTM模型的方差更小，稳健性更强。通过计算得到SCM-LASSO模型10期预测的平均相对误差为6.47%，MSE 为9.28；ANN 的平均相对误差为3.59%，MSE 为2.98；LSTM 的平均相对误差为2.28%，MSE 为1.36，由此可得LSTM 的预测效果较好。表3 显示了不同模型在20 折交叉验证测试集上的预测误差，包括均方误差MSE和平均绝对误差MAE。由表3可以看出，SCM-LASSO的均方误差和平均绝对误差最大，分别为6.20和2.98，预测精度最低；其次是ANN，分别为3.20和1.96；最后为LSTM，分别为2.57 和1.43。且LSTM 的误差标准差也最小，由此可见长短期记忆模型预测精度更优，鲁棒性更强，因此更加适用于反事实结果的预测。

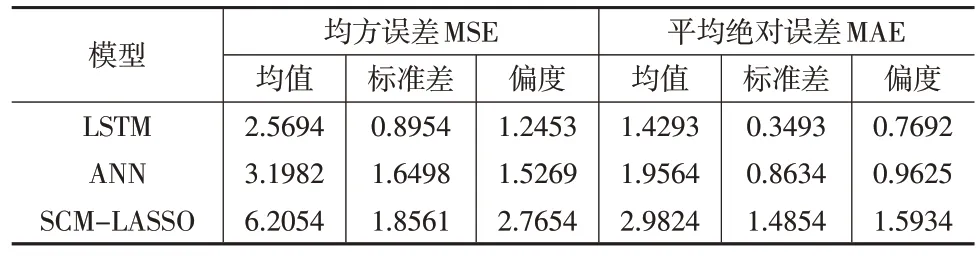
表3 模型交叉验证预测误差对比

2.2 政策效应评估应用

2.2.1 评估应用

反事实预测是政策效应评估中的关键环节，将反事实预测结果与实际值作差即可得到平均处理效应[15,16]，而RDD、DID和SCM方法的反事实预测结果均存在一定的误差效应，本文引入LSTM 深度学习网络提高预测精度，并剔除模型的误差效应，改善评估结果。由于在政策干预时点附近模型的预测误差具有一定的普适性，因此可以在政策干预点前设置一段测试集，预先测定模型在测试集上的误差效应。将政策干预后的平均处理效应与测试集上预先测定的误差效应作差，即可得到政策效应的有效评估。基于此，本文测定模型政策效应为平均处理效应与模型误差效应的差值，即政策干预后若干期实际结果与模型反事实预测结果的平均相对误差与政策干预时点前测试集上模型预测结果的平均相对误差的差值。

2.2.2 结果分析

本文以湖北省财政厅2018年3月公布的《湖北省进出口政策性优惠利率贷款贴息实施方案》为例，测定该政策方案对湖北省外贸进出口的政策效应，该方案引导湖北省进出口银行投放更多优惠贷款金额，促进企业高新技术产品、关键资源、技术以及零部件的进口，通过省内外工程承包、股权收购等经济活动来刺激贸易额的增长，对于湖北省外贸进出口总额增长具有一定的促进作用。观察相关数据可以发现，政策发布节点前后湖北省外贸进出口总额发生了较大幅度变化，说明该项政策具有一定的政策调控效应。基于此，以2018年3月作为政策干预点对数据进行划分，分别使用构造的LSTM、SCM-LASSO 和ANN 对政策干预前的外贸进出口总额进行训练拟合，对政策干预后的结果进行反事实预测，测算出模型平均处理效应。选定政策干预后的10 期数据计算平均处理效应，由于测试集的数据时点（2017 年3 月至2018 年2 月）与政策干预节点（2018年3月）极为接近，因此本文以测试集上模型的平均相对误差作为政策干预后10 期数据的误差效应，并以此量化估计该项方案带来的经济效益。图4 展示了不同模型在测试集上的相对误差。

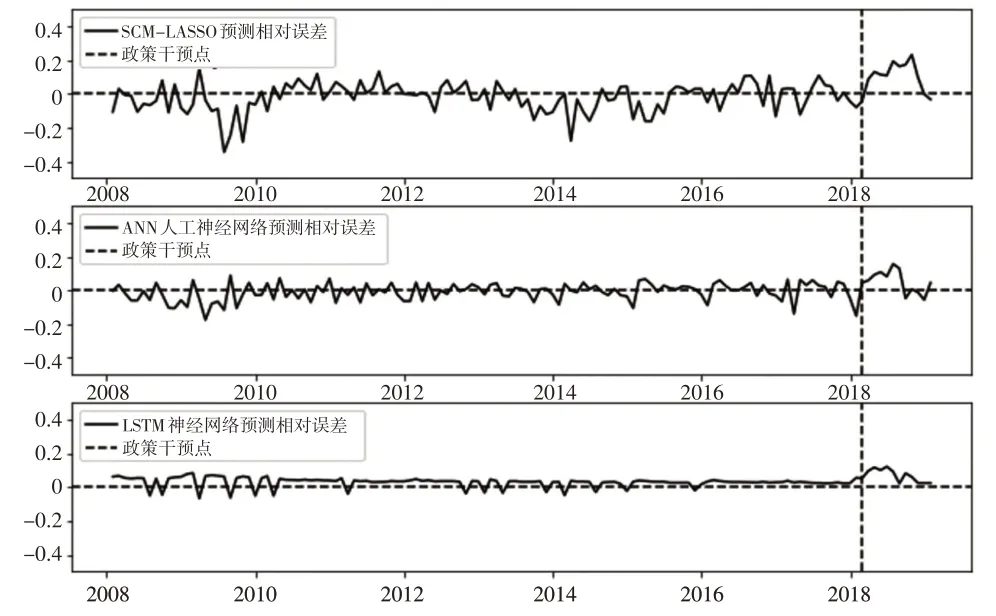
图4 预测模型的误差效应

图4 中的横实线为各模型预测外贸进出口总额时的相对误差，竖虚线为进出口优惠政策干预时点，可以看出，三条误差线与0值线存在一定的偏离，说明三种模型均具有一定的误差效应，其中LSTM 的预测误差偏离最小，波动性最小，稳健性最强，拟合效果最好。此外，通过观察发现，三条误差线在政策干预时点处均具有较大幅度的波动，说明除误差效应外，该项进出口优惠政策对湖北省当期外贸经济活动也产生了较大影响，即波动项包含了模型误差效应和政策调控效应。为此，需要将模型误差效应剔除以获得更为精准的效应评估结果。将不同模型预测得到的平均处理效应和误差效应作差，即可得到对应的政策效应评估结果。表4 列出了三种模型测算的政策效应结果以及对应的平均处理效应和误差效应。

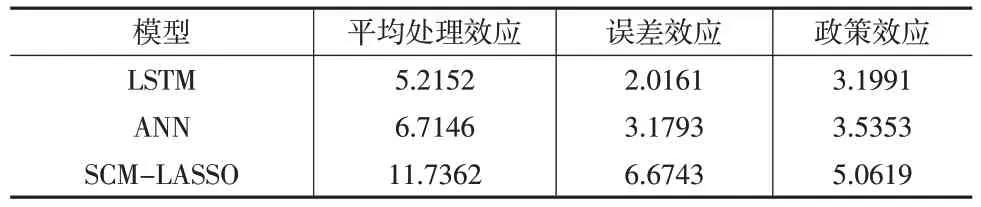
表4 三种模型测算的因果效应 （单位：%）

由表4 中的结果可以发现：首先，从平均处理效应预测结果来看，LSTM预测得到的平均处理效应和ANN人工神经网络测算结果较为接近，而SCM-LASSO 的评估结果为11.74%，说明SCM-LASSO对该项外贸政策的效益评价可能存在高估。其次，从误差效应结果来看，LSTM的相对误差最小，为2.21%；ANN 其次，为3.18%；SCM-LASSO 最高，为6.67%。说明LSTM 的预测误差更低，稳健性更强。最后，从政策效应评估结果来看，若不考虑模型误差效应，LSTM 的测算结果显示该政策为湖北省外贸经济带来了5.22%左右的经济效益增长，ANN 和SCM-LASSO 则分别估计出6.71%和11.74%的增长效益，通过考虑三种方法的误差效应，发现LSTM 的最终评估效益为3.20%左右，而ANN与SCM-LASSO评估结果为3.54%和5.06%，比较可知LSTM的修正效应最小。由此可见，本文构造的基于LSTM的政策效应预测模型精度更高，适用性更好，可以有效地测算优惠贷款利率政策对湖北省进出口贸易总额的影响。

3 结束语

本文提出了一种基于LSTM的政策效应评估方法，融合机器学习和政策评估应用，利用机器学习的优良预测性能对政策方案的平均处理效应进行预测，同时剔除预测模型的误差效应，最终测算得出有效的评估结果。以2018年3月公布的《湖北省进出口政策性优惠利率贷款贴息实施方案》为例，本文使用LSTM 模型对该方案的政策效应进行了预测和评定，同时构造了基于合成控制思想的SCM-LASSO 回归和ANN 人工神经网络作为对比模型进行了比较，利用交叉验证选取不同模型的最优参数。基于湖北省2008 年1 月至2021 年10 月的外贸进出口总额数据，本文从实证角度比较分析了构造模型的政策效应预测精度。研究结果如下：（1）LSTM 由于存在长期记忆性特性，在训练集前期可借鉴信息较少，拟合效果较ANN 略差，但是在训练集后期以及测试集未知数据上表现优良，说明深度学习技术的引入可以显著提高反事实结果的预测精度。（2）基于合成控制思想的SCM-LASSO预测模型具有良好的数据拟合效果，但是在预测精度上与ANN、LSTM还存在一定的差距。（3）LSTM 的估计结果显示，外贸贷款优惠利率政策为湖北省外贸经济带来了3.2%左右的经济效益增长，而SCM-LASSO 高估了其带来的经济效益。基于深度学习方法的预测精度更高，误差效应更低，修正效应最小，效应评估结果更为准确。

本文提出的模型误差效应是对政策因果效应评估方法的一种尝试，由于多数研究均通过测算平均处理效应来衡量政策效应，而忽略了模型预测本身带来的误差效应，因此，本文以政策干预点附近测试集的平均相对误差作为政策干预后模型预测的误差效应，结合平均处理效应可以得到更为准确的政策效应评估结果，在一定程度上可以避免模型本身带来的评估误差。