矩阵方程X+A*(R+B*XB)-tA=Q的Hermite正定解
黄玉莲, 罗显康
(1.宜宾学院 理学部, 四川 宜宾 644000; 2. 宜宾市南溪职业技术学校, 四川 宜宾 644100)
0 引言
研究非线性矩阵方程
X+A*(R+B*XB)-tA=Q
(1)
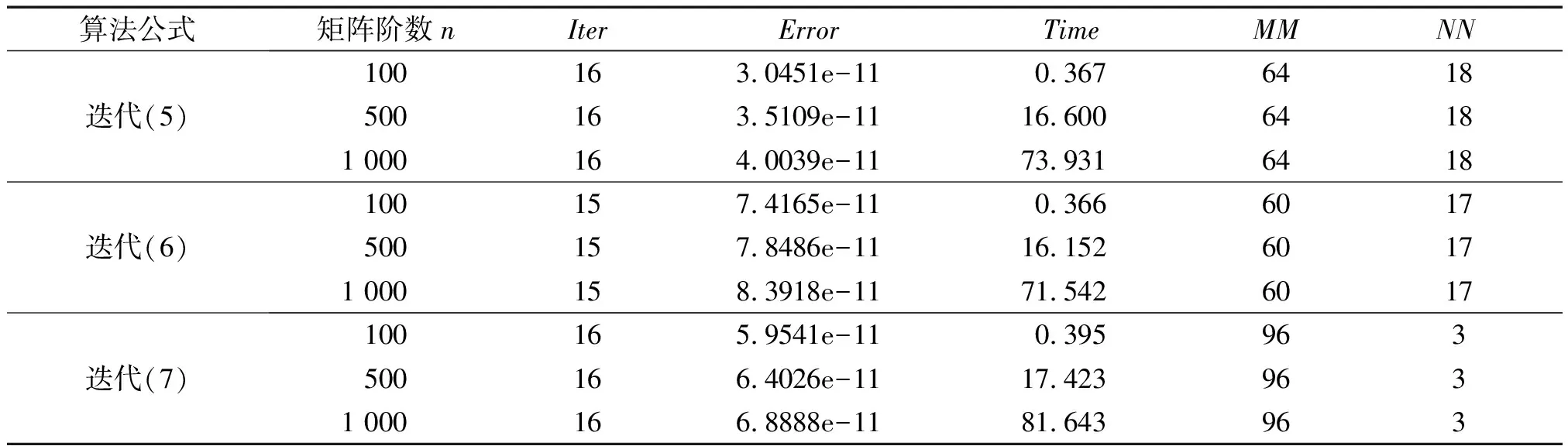
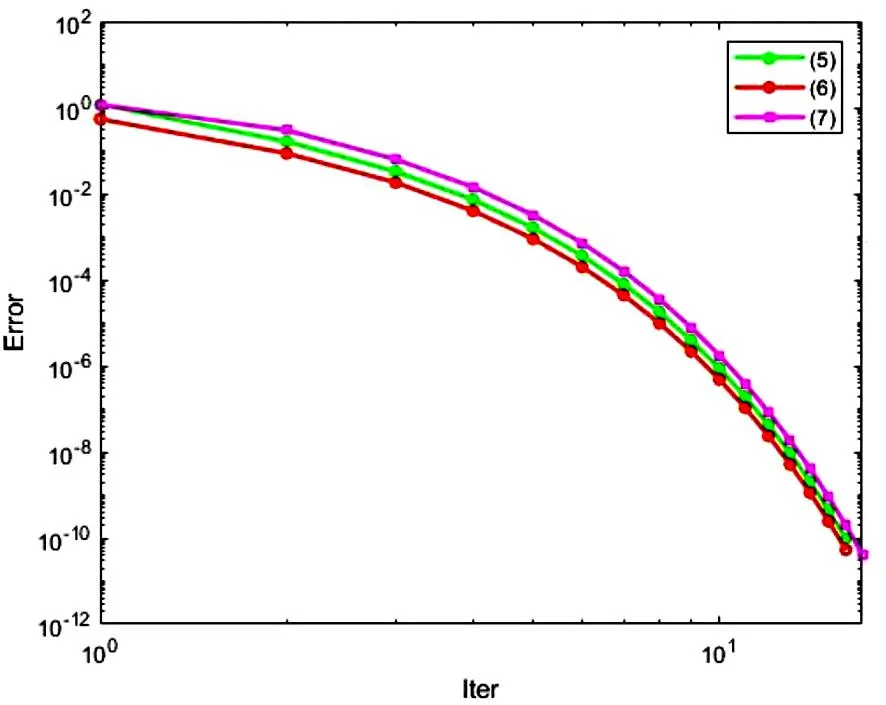
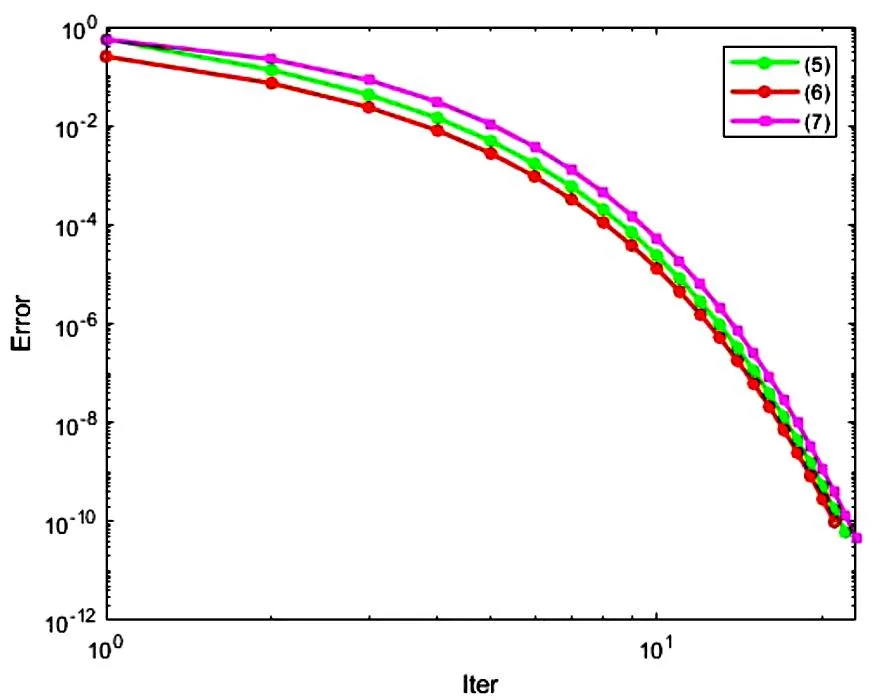
的Hermite正定解, 其中t≥1是正实数,A,B,R,Q是n阶非奇异复矩阵且R,Q正定. 非线性矩阵方程是数值代数的研究热点之一, 在最优控制理论、动态规划、统计学、随机过程、动态规划和梯形网络等领域的应用十分广泛[1-5]. 矩阵方程(1)是时间代数Riccati方程特殊情形的推广, 众多专家学者对其各种简化形式进行了讨论[6-8]. 近年来, 不断有学者对形如方程(1)的非线性矩阵方程进行了系统研究, 取得很多丰硕成果. 文献[9]利用Thompson度量的性质和系数矩阵的特征值刻画了矩阵方程X-A*(R+BXB*)-tA=Q的Hermite正定解, 构造出带步长参数的迭代算法. 文献[10]给出方程X=H+AHX(I+GX)-1A存在Hermite正定解的充分条件, 提出了一种加速算法. 文献[11]利用矩阵方程X=Q-A*(Im⊗X-C)-tA的等价形式, 提出计算方程Hermite正定解的牛顿迭代法. 文献[12]构造出几种求解矩阵方程X+A*(R+B*XB)-tA=Q(0 符号说明: 本文用M>0(M≥0)表示M是正定(半正定)矩阵,M>N(M≥N)表示M-N是正定(半正定)矩阵,A*表示复矩阵A的共轭转置. 对于正定矩阵Q, 用λmax(Q)和λmin(Q)分别表示矩阵Q的最大特征值和最小特征值. ‖H‖表示矩阵H的谱范数.B-*=(B-1)*. 本节先给出方程(1)存在Hermite正定解的充分条件, 证明在给定条件下方程存在唯一Hermite正定解. 同时得到方程Hermite正定解的取值范围及性质. 引理1[3]若A>B>0(A≥B>0), 则当α∈(0,1]时, 有Aα>Bα>0(Aα≥Bα>0); 当α∈[-1,0)时, 有0 引理2[3]对任意正定矩阵E,F≥bI>O及正数t, 都有 引理3[3]若C和P是相同阶数的Hermite矩阵且P可逆, 则CPC+P-1≥2C. 引理4[13]设A,B是Hilbert空间H上的正算子, 且满足M1I≥A≥m1I,M2I≥B≥m2I和B≥A≥O, 则对任意的t∈[1,+∞), 有 引理5[13]设矩阵A,B,D∈Cn×n, 且A,A-BD和DA-1B-I非奇异, 则 (A-BD)-1=A-1-A-1B(DA-1B-I)-1BA-1. 定理1若方程(1)存在Hermite正定解, 则 (B*)-1[(AQ-1A*)1/t-R]B-1 证明因X是矩阵方程(1)的Hermite正定解, 则有 X 因此(R+B*XB)-t<(A*)-1QA-1, 从而(R+B*XB)t>AQ-1A*. 再根据引理1, 有 X>(B*)-1[(AQ-1A*)1/t-R]B-1. 于是(B*)-1[(AQ-1A*)1/t-R]B-1 定理2若(AQ-1A*)1/t>R且 显然Ω是一个非空的有界闭凸集, 且F(X)在Ω上是连续的. 因为 则对任意的X∈Ω, 都有 (2) 又因为F(X)=(B*)-1[(A(Q-X)-1A*)1/t-R]B-1>(B*)-1[(AQ-1A*)1/t-R]B-1>O, 则有F(X)∈Ω.因此F(X)⊆Ω, 由Brouwer不动点定理知,F(X)在Ω上存在不动点, 即X=F(X)=(B*)-1[(A(Q-X)-1A*)1/t-R]B-1. 此不动点即为矩阵方程(1)的一个Hermite正定解. 由定理1知∀X1,X2∈Ω, 有X1,X2≥(B*)-1[(AQ-1A*)1/t-R]B-1, 那么 (R+B*X1B),(R+B*X2B)≥ (AQ-1A*)1/t≥λmin(AQ-1A*)1/t, (3) 令λmin(AQ-1A*)1/t=b, 由(3)式和引理2可知 定理3若矩阵方程(1)有Hermite正定解X, 则X∈[N,M]. 其中 证明由定理1知 (B*)-1[(AQ-1A*)1/t-R]B-1 则有R+B*XB 于是有 进而 因此 即有 A*(R+B*QB)-tA=M. 由引理5得 (R+B*XB)t=A(Q-X)-1A*=A[Q-1-Q-1(XQ-1-I)-1XQ-1]A*=AQ-1A*-AQ-1(XQ-1-I)-1XQ-1A*=AQ-1A*-AQ-1(Q-1-X-1)-1Q-1A*=AQ-1A*+AQ-1(X-1-Q-1)-1Q-1A*>AQ-1A*+AQ-1(B[(AQ-1A*)1/t-R]-1B*-Q-1)-1Q-1A*. 因此 X>(B*)-1[[AQ-1A*+AQ-1(B[(AQ-1A*)1/t-R]-1B*-Q-1)-1Q-1A*]1/t-R]B-1=N. 即X∈[N,M]. 证毕. 定理4若矩阵方程(1)存在Hermite正定解, 则有 证明因X为矩阵方程(1)的Hermite正定解, 即X+A*(R+B*XB)-tA=Q.则有 0 由引理1得 X>(B*)-1[(AQ-1A*)1/t-R]B-1. 因此 R+B*QB>R+B*XB= [A(Q-X)-1A*]1/t> [A(Q-(B*)-1[(AQ-1A*)1/t-R]B-1)-1A*]1/t. (4) 即 证毕. 本节给出求解矩阵方程(1)的迭代算法, 并分别证明其收敛性. 先讨论如下迭代: (5) 定理5在定理2的条件下, 由算法公式(5)生成的序列{Xk}收敛到矩阵方程(1)的一个Hermite正定解. 证明由定理2可知矩阵方程(1)存在Hermite正定解, 即 X=(B*)-1[(A(Q-X)-1A*)1/t-R]B-1>X0. 根据算法公式(5)知 X1=(B*)-1[(A(Q-X0)-1A*)1/t-R]B-1= (B*)-1[(AQ-1A*)1/t-R]B-1>O=X0,X1=(B*)-1[(A(Q-X0)-1A*)1/t-R]B-1< (B*)-1[(A(Q-X)-1A*)1/t-R]B-1=X. 假设对任意k≥1有Xk-1 Xk+1=(B*)-1[(A(Q-Xk)-1A*)1/t-R]B-1> (B*)-1[(A(Q-Xk-1)-1A*)1/t-R]B-1=Xk,Xk+1=(B*)-1[(A(Q-Xk)-1A*)1/t-R]B-1< (B*)-1[(AQ-X)-1A*)1/t-R]B-1=X. 由数学归纳法和矩阵偏序可知迭代序列{Xk}单调递增有上确界, 收敛于矩阵方程(1)的一个Hermite正定解.证毕. 下面对算法公式(5)进行改进 (6) 对于算法公式(6), 有如下结论. 定理6若存在实数ξ,η(0<ξ≤η<1)满足 则算法公式(6)生成的序列{Xk}收敛于矩阵方程(1)的一个Hermite正定解X, 且有ξQ≤X≤ηQ. 证明因为Q是Hermite 正定矩阵, 则AQ-1A*也为Hermite 正定矩阵, 那么 λmin(AQ-1A*)I≤AQ-1A*≤λmax(AQ-1A*)I. 并且 根据算法公式(6)可知 假设对任意k≥1有Xk≥Xk-1, 那么 Xk+1=(B*)-1[(A(Q-Xk)-1A*)1/t-R]B-1≥ (B*)-1[(A(Q-Xk-1)-1A*)1/t-R]B-1=Xk. 由归纳法知迭代序列{Xk}单调递减有下界ξQ.下面证明迭代序列{Xk}有上界ηQ, 由于X0=ξQ≤ηQ,易知 假设对任意k≥1有Xk≤ηQ, 那么 综上所述, 由算法公式(6)生成的序列{Xk}单调递增有上界, 由单调有界定理知, 序列{Xk}收敛于矩阵方程(1)的一个Hermite正定解, 且满足ξQ≤X≤ηQ.证毕. 定理7若存在实数ξ,η(0<ξ≤η<1)满足 则矩阵方程(1)存在Hermite正定解且有 ‖Xk-X‖≤p‖Xk-1-X‖≤pk(η-ξ)‖Q‖. 证明由定理6知, 算法公式(6)产生的序列{Xk}收敛到矩阵方程(1)的一个Hermite正定解, 令M=A(Q-Xk-1)-1A*,N=A(Q-X)-1A*, 则 M,N≥ξ·B*QB+R≥λmin(ξ·B*QB+R)I. 取b=λmin(ξ·B*QB+R), 对范数‖Xk-X‖进行估计 因此 ‖Xk-X‖≤q‖Xk-1-X‖≤ qk‖X0-X‖≤qk(η-ξ)‖Q‖. 证毕. 为降低运算复杂度, 避免每步迭代过程中矩阵求逆引起的误差, 提出如下免逆迭代: (7) 定理8在定理2的条件下, 由算法公式(7)生成的序列{Xk}和{Yk}满足 证明由定理2知方程(1)的Hermite正定解满足X=(B*)-1[(A(Q-X)-1A*)1/t-R]B-1. 则 X1=(B*)-1[(AY0A*)1/t-R]B-1= (B*)-1[(AQ-1A*)1/t-R]B-1 由引理3得 Y1=[2I-Y0(Q-X1)]Y0= 2Y0-Y0(Q-X1)Y0≤(Q-X1)-1≤(Q-X)-1,Y1-Y0=Y0-Y0(Q-X1)Y0=Q-1X1Q-1>O. 则有 X0 假设 Xk-1 那么 Xk+1=(B*)-1[(AYkA*)1/t-R]B-1< (B*)-1[(A(Q-X)-1A*)1/t-R]B-1=X,Xk+1=(B*)-1[(AYkA*)1/t-R]B-1> (B*)-1[(AYk-1A*)1/t-R]B-1=Xk,Yk+1=2Yk-Yk(Q-Xk+1)Yk≤ (Q-Xk+1)-1≤(Q-X)-1,Yk+1-Yk=Yk-Yk(Q-Xk+1)Yk=Yk[Yk-1-(Q-Xk+1)]Yk>Yk[Yk-1-(Q-X)]Yk>0. 综上所述, 由算法公式(7)生成的序列{Xk}和{Yk}皆单调递增有上界, 根据单调有界定理知, 序列{Xk}收敛于矩阵方程(1)的一个Hermite正定解. 证毕. 本节利用数值算例验证本文的理论成果, 说明所提迭代算法的有效性. 算法实现的软件环境是MATLAB R2018b, PC机为Intel(R) Core(TM) i7-8750H cpu @ 2.20GHz. 实验报告中, 用k、MM、NN、Error和Time分别代表迭代次数、算法所需矩阵乘法运算次数、矩阵求逆次数、终止时的残差和计算所需时间. 算法停止条件为 Rk=‖Xk+A*(R+B*XkB)-t-Q‖≤1.0×10-10. 例1给定n阶复矩阵A,B,R,Q∈Cn×n,且R,Q为Hermite正定矩阵. 试求矩阵方程X+A*(R+B*XB)-1.8A=Q的Hermite正定解. 解当n=5时, 直接验证可知满足定理2矩阵方程存在Hermite正定解的条件. 取ξ=0.1,η=0.7, 满足定理6的条件. 残差与迭代次数结果如图1所示, 迭代计算结果如下: 表1 例1迭代计算结果 图1 例1残差迭代结果 当n=100,500,1 000时, 计算结果如表1所示. 例2给定n阶复矩阵A,B,R,Q∈Cn×n, 且R,Q为Hermite正定矩阵. 试求矩阵方程X+A*(R+B*XB)-3A=Q的Hermite正定解. 解当n=5时, 直接验证可知满足定理2矩阵方程存在Hermite正定解的条件. 取ξ=0.2,η=0.8, 满足定理6的条件. 残差与迭代次数结果如图2所示, 迭代计算结果如下: 图2 例2残差结果 表2 例2迭代计算结果 当n=100,500,1 000时, 计算结果如表2所示. 表1、表2结果显示, 三种迭代算法经较少迭代次数均能达到预设误差精度, 收敛速度较高. 不动点迭代算法涉及的矩阵求逆次数比无逆迭代算法次数多, 但涉及的矩阵乘法次数较少.迭代公式(6)在选取适当参数时, 其收敛速度更快, 迭代公式(7)的优势在于每步迭代过程中仅涉及初始矩阵求逆. 非线性矩阵方程X+A*(R+B*XB)-tA=Q是离散时间代数Riccati方程的特殊情形. 本文在一定条件下讨论其Hermite正定解, 给出Hermite正定解的一些性质及其取值区间. 构造出计算此方程的不动点迭代算法和无逆迭代算法, 从降低矩阵求逆运算误差的角度对比分析了两类算法的特点. 数值算例表明, 所提出的算法对求解此类非线性矩阵方程可行、有效.1 解的存在性及上下界估计
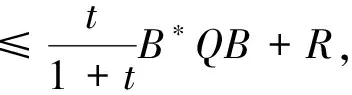
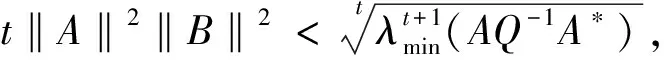
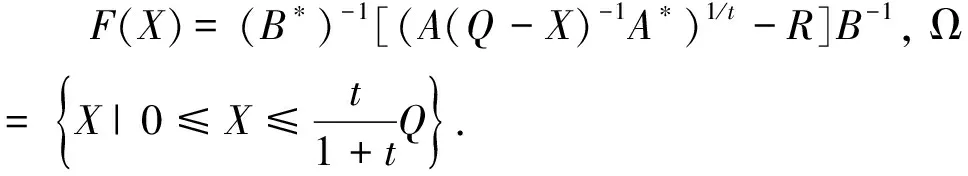
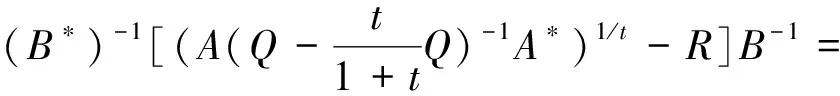



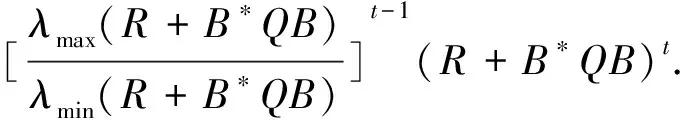
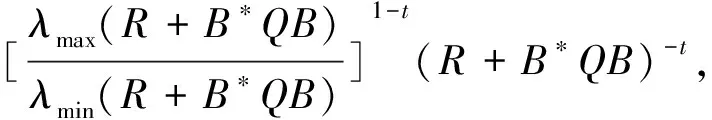
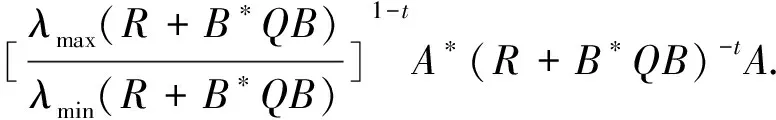
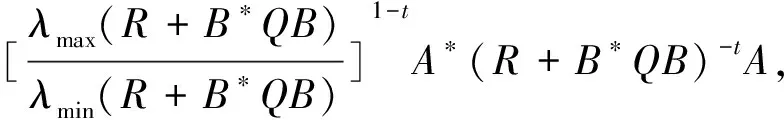


2 求解矩阵方程(1)的迭代算法
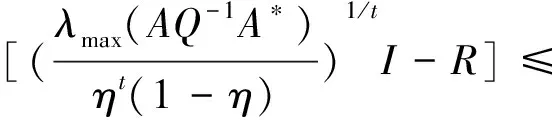
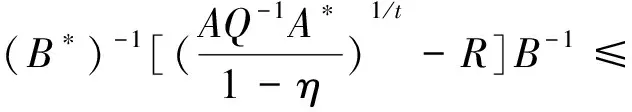
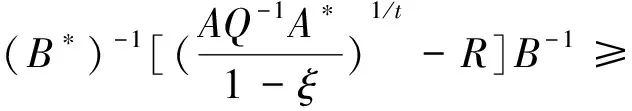
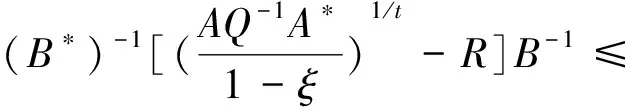
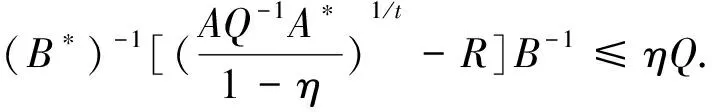
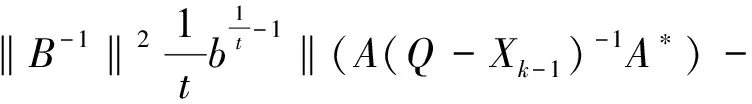
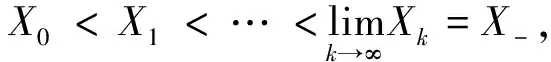
3 数值算例



4 结论

