布尔矩阵的对偶块关系矩阵及其行列空间格的容差关系

王思雨, 罗从文

(三峡大学 理学院, 湖北 宜昌 443002)

0 引言

概念格作为形式概念分析的核心数据结构,能够用来进行分类、聚类和提取规则. Ganter等[1]首先提出了块关系和容差关系的概念,容差关系描述了概念格中概念的归类和划分关系,而块关系反映了形式背景经过变换后形成的概念格中的外延与内涵仍然是原背景中的.已经证明了有一个块关系就存在一个容差关系与之对应,即形式背景的块关系构成的格同构于概念格的容差关系构成的格. 由容差关系可以诱导出商格,得到的商格同构于块关系的概念格. Konecny等[2]将块关系的概念推广到模糊集上,得到块L-关系和完全L-容差的概念,证明了块L-关系的L-集合与完全L-容差的L-集合同构. 杨凯等[3]运用容差关系和块关系一一对应的关系,从概念间亏值的角度出发,通过亏值计算实现了由容差关系找出与之对应的块关系,为亏值理论在形式概念与分析知识体系中的结合与应用提供了扩展和思路. 关于容差关系及其商格的更多结论具体可参见文献[4-5].

仅由0和1这两个元素组成的布尔矩阵有着极其简单、清晰的形式. 在关系理论、逻辑学、模糊数学、图论、格论、代数半群理论、组合论、计算机科学等领域有着密切的联系和应用. 文献[6-9]用矩阵的语言刻画形式背景的概念格,构造了由一个布尔矩阵的特定行指标和列指标对所确定的指标格,得到了布尔矩阵指标格的一些基本性质,研究了有限格同构于布尔矩阵的指标格的充要条件. 以上定义的布尔矩阵的指标格同构于与之对应的形式背景的概念格. 郭玲等[10]将块关系推广到布尔矩阵上,给出布尔矩阵的块关系矩阵的概念,运用布尔矩阵指标格的性质证明了布尔矩阵的块关系矩阵构成的格同构于布尔矩阵指标格的容差关系构成的格. Luo等[6]从对偶的角度刻画了布尔矩阵的指标格也叫作布尔矩阵的行列空间格,给出了布尔矩阵的行列空间格中元素交和并运算、有限格同构于行列空间格的充要条件、同余矩阵构成的格与由同余矩阵诱导的商格的关系. 布尔矩阵的行列空间格对偶同构于布尔矩阵的指标格. 关于格论和布尔矩阵的更多结论具体可参见文献[11-12].

在以上结论的基础上,本文主要研究布尔矩阵的对偶块关系矩阵及其行列空间格的容差关系. 给定一个布尔矩阵的对偶块关系矩阵,如何找到与之对应的布尔矩阵的行列空间格的容差关系;反之,给定布尔矩阵的行列空间格的容差关系,如何找到与之对应的布尔矩阵的对偶块关系矩阵. 在第一部分,介绍了布尔矩阵的行列空间格的概念和基本性质,引入布尔矩阵的对偶块关系矩阵的概念. 在第二部分,首先建立了布尔矩阵的对偶块关系矩阵与其行列空间格的容差关系之间的联系,进而证明了布尔矩阵的对偶块关系矩阵形成的格同构于行列空间格的容差关系形成的格,最后得到了由容差关系诱导的商格同构于对偶块关系矩阵的行列空间格.

定义为(aij∧bij)m×n,其中

1 预备知识

具体可参见文献[7].

由定义1容易得出以下性质.

性质1设A=(aij)m×n∈βmn,对于集合

有:

1)R1⊆R2⟹R2′⊆R1′,

1′)W1⊆W2⟹W2′⊆W1′;

2)R″⊆R,

2′)W″⊆W;

3)R′=R‴,

3′)W′=W‴;

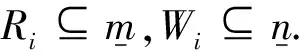
引理1设A=(aij)m×n∈βmn,定义集合

则CR(A)关于运算∧和∨构成一个格,其中∧和∨定义如下:

(R1,W1)∧(R2,W2)=(R1∪R2,(W1∩W2)′′), (R1,W1)∨(R2,W2)=((R1∩R2)′′,W1∪W2),

则称CR(A)是A的行列空间格.

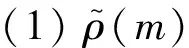
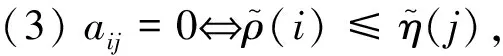
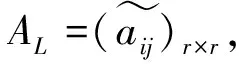
关于性质1、性质2、引理1的具体内容,可参见文献[7].

定义2[1]设V是一个格,V上的一个容差关系θ指关系θ⊆V×V满足自反性、对称性且关于格V的交和并运算相容,即对a,b,c∈V,有

aθb⟹(a∧c)θ(b∧c),(a∨c)θ(b∨c),

容易证明格V上的所有容差关系的集合关于集合的包含关系形成一个格,记作Tol(V)[13].

引理2[1]若θ是格V上的一个容差关系,则有aθb,x,y∈[a∧b,a∨b]⟹xθy.

定义3[1]若θ是有限格V上的一个容差关系,对于任意a∈V,定义:

aθ:=∧{b∈V|aθb},aθ:=∨{b∈V|aθb},

则区间[a]θ=[aθ,(aθ)θ]叫作θ的一个块.

定义4设A=(aij)m×n,B=(bij)m×n∈βmn,称B是A的一个对偶块关系矩阵指下列条件成立:

1)A≥B;

例1设

则A的行列空间格CR(A)如图1所示.容易得出B是A的对偶块关系矩阵.

因为A≥B且对每个

有:

B1*=B2*={67}∈R(A),B3*=B4*={∅}∈R(A),B5*=B6*={12}∈R(A),B7*={1267}∈R(A).B*1=B*2={567}∈C(A),B*3=B*4=B*5={∅}∈C(A),B*6=B*7={127}∈C(A).

即Bi*∈R(A),B*j∈C(A).

图1 矩阵A的行列空间格CR(A)

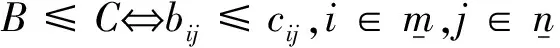
2 主要定理及结论

定理1设A=(aij)m×n∈βmn,θ是CR(A)上的一个容差关系,定义矩阵B=(bij)∈βmn如下:bij=0⟺ρ(i)θ(ρ(i)∧η(j)),则B是A的对偶块关系矩阵.

证明设aij=0,由引理1可知ρ(i)≤η(j).由已知θ是CR(A)上的一个容差关系,所以ρ(i)θρ(i),即ρ(i)θ(ρ(i)∧η(j)),因此bij=0,故A≥B.

要证明Bi*∈R(A),只需考虑这个元素

η(j0)≥∧{η(j)|ρ(i)θ(ρ(i)∧η(j))},

因此有

ρ(i)∧η(j0)≥ ∧{ρ(i)∧η(j)|ρ(i)θ(ρ(i)∧η(j))},

综上所述B是A的一个对偶块关系矩阵.

定理2设A=(aij)m×n∈βmn,B是A的一个对偶块关系矩阵,对任意的(R,W),(U,V)∈CR(A),定义τ(B)如下:

(R,W)τ(B)(U,V)⟺B≤A(R,V)∩A(U,W),

则τ(B)是CR(A)上的一个容差关系.

证明设(R,W)∈CR(A),显然有

RA⊆W⟺WA⊆R⟺A≤A(R,W).

由于B=(bij)m×n是对偶块关系矩阵,则有B≤A≤A(R,W),从而有

B≤A(R,W)∩A(R,W)⟺(R,W)τ(B)(R,W),

则τ(B)满足自反性.

设(R,W),(U,V)∈CR(A),假设(R,W)τ(B)(U,V),则

(R,W)τ(B)(U,V)⟺B≤A(R,V)∩A(U,W)⟺B≤A(U,W)∩A(R,V)⟺(U,V)τ(B)(R,W),

则τ(B)满足对称性.

下证τ(B)对交和并运算满足相容性.

若T是一个指标集,且有元素满足

(Rt,Wt)τ(B)(Ut,Vt),t∈T,

我们的论点如下:由于

(Rt,Wt)τ(B)(Ut,Vt)⟺B≤A(Rt,Vt)∩A(Ut,Wt),

则有B≤A(Rt,Vt),从而有

RtB⊆Vt=UtA⟹RtBA⊇VtA=Ut.

又由于

即

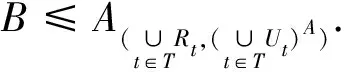
则τ(B)是CR(A)上的一个容差关系.

定理3设A=(aij)m×n∈βmn,则A的行列空间格CR(A)上的所有容差关系形成的格Tol(CR(A))同构于A的所有对偶块关系矩阵形成的格BR(A),即映射:

其中β(θ)=(bij)∈βmn满足:bij=0⟺ρ(i)θ(ρ(i)∧η(j)),是一个格同构映射.

证明令:

下证1θ=τβ(θ),1B=βτ(B).显然β和τ都是保序映射.设θ是CR(A)上的一个容差关系,我们需要证明:

(R,W)θ(U,V)⟺(R,W)τ(β(θ))(U,V),

其中β(θ)=(bij)m×n∈βmn.

根据引理2,不妨设

(R,W)>(U,V)⟺R⊆U⟺V⊆W.

对所有的

即对所有的

bij=0.又

即证1θ=τβ(θ).

设矩阵B=(bij)m×n∈βmn是矩阵A的对偶块关系矩阵,则

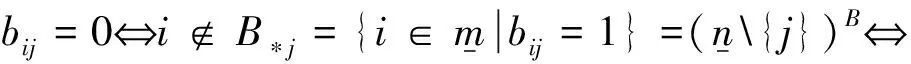
又因为

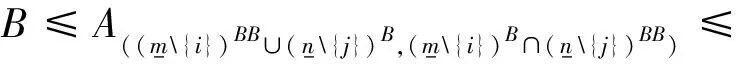
β(τ(B))中第i行,第j列元素为0.

因此B=β(τ(B)),即1B=βτ(B).

定理4设A=(aij)m×n∈βmn,若θ是CR(A)上的一个容差关系且B与θ对应的对偶块关系矩阵,则有CR(A)/θ≅CR(B),更准确地,有:

1)映射[(WA,W),(R,RA)]是θ的一个块当且仅当(R,W)∈CR(B).

证明根据定理3,设

(WA,W),(R,RA)∈CR(A),

且(WA,W)≤(R,RA),则((WA,W),(R,RA))∈θ当且仅当B≤A(R,W),即RB⊆W,WB⊆R.对任意的(X,Y)∈CR(B),则有(X,Y)θ=(XBA,XB)且(X,Y)θ=(YB,YBA),因此((X,Y)θ)θ=(XBB,XBBA).

若令W=XB,R=XBB,根据引理1,有(R,W)∈CR(B),且

[(X,Y)]θ=[(X,Y)θ,((X,Y)θ)θ]=

[(XBa,XB),(XBB,XBBA)]=

[(WA,W),(R,RA)].

3 总结

根据布尔矩阵行列空间格的性质,文章首先给出了布尔矩阵的对偶块关系矩阵的定义. 给定布尔矩阵的行列空间格的容差关系,由性质1、引理1可以得到与之对应的布尔矩阵的对偶块关系矩阵;反之,给定布尔矩阵的对偶块关系矩阵,由性质1、性质2可以得到与之对应的布尔矩阵的行列空间格的容差关系. 因此存在从布尔矩阵的行列空间格上的所有容差关系形成的格到布尔矩阵的对偶块关系矩阵形成的格的映射,并推导出此映射是一个同构映射. 证明了由容差关系诱导的商格同构于对偶块关系矩阵的行列空间格.