双参数Weibull分布尺度参数的Bayes估计和经验Bayes估计

董秋灿, 徐 宝

(吉林师范大学 数学与计算机学院, 吉林 四平 136000)

0 引言

1951年,瑞典物理学家Waloddi Weibull提出了Weibull分布,该分布一经提出就吸引了众多学者的关注.文献[1]研究了Weibull分布在可靠性与生存分析等方面的应用;文献[2]在随机截尾采样下,对Weibull分布失效数据的可靠性进行了分析;文献[3-4]讨论了Weibull分布的矩估计、极大似然估计和区间估计;文献[5]研究了Weibull分布尺度参数变点模型的参数估计问题;文献[6-7]在复合Linex对称损失下,研究了逆Weibull分布尺度参数的E-Bayes估计;文献[8]在平方损失函数下研究了NA样本Weibull分布刻度参数的经验Bayes估计;文献[9]讨论了在删失截断情形下Weibull分布多变点模型的参数估计,并利用MCMC算法验证了估计的精确性,这些成果都丰富了Weibull分布参数估计的研究. 但在加权p,q对称熵损失函数下对Weibull分布参数的Bayes估计和经验Bayes估计的研究较少,因此本文在已有研究的基础上,使用加权p,q对称熵损失函数

(1)

研究双参数Weibull分布尺度参数的Bayes估计和经验Bayes估计. 首先给出了逆Gamma先验分布下尺度参数的Bayes估计的精确形式,然后利用所得Bayes估计得到了Weibull分布尺度参数的经验Bayes估计,最后利用R语言编程进行数值模拟,验证参数估计的精确性.

双参数Weibull分布的密度函数和分布函数分别为

(2)

其中η=θm,m为形状参数,η为尺度参数,记为W(m,η).

1 Weibull分布尺度参数的Bayes估计

首先给出Weibull分布的尺度参数在任意先验下Bayes估计的一般形式.

定理1设X=(X1,X2,…,Xn)为取自Weibull总体(2)的一组简单随机样本,在加权p,q对称熵损失函数(1)下,对于任意的先验分布,尺度参数η的Bayes估计为

证明在加权p,q对称熵损失函数L(η,δ)下,δ对应的Bayes风险函数为

R(δ)=E(L(η,δ))=E(E(L(η,δ)|X)).

由于

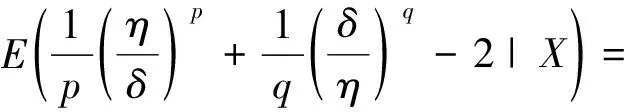
如果使R(δ)达到最小,那么只需让E(L(η,δ)|X)达到最小值,令

针对φ(X)使得对δ求导并令其为0,得到

解得

其次研究Weibull分布在逆Gamma分布下尺度参数Bayes估计的表达式.

定理2在加权p,q对称熵损失函数(1)下,若Weibull分布(2)的尺度参数η的先验分布为逆Gamma分布Γ-1(α,λ),则尺度参数η的Bayes估计为

(3)

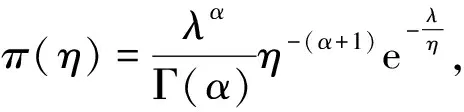
所以参数η的后验分布为

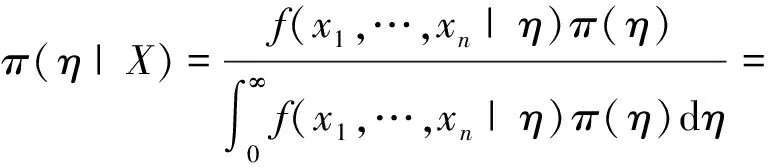
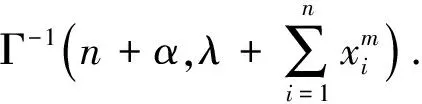
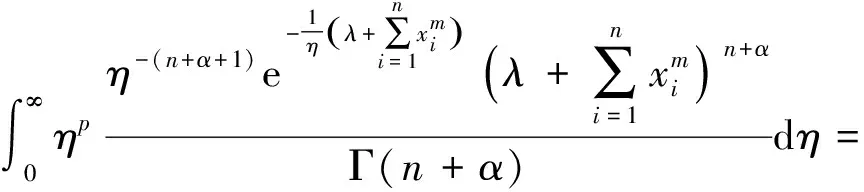
同理得到

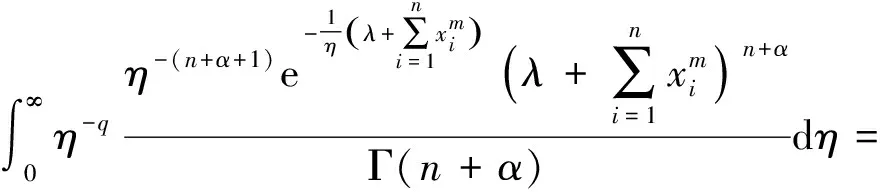
因此可以得到在加权p,q对称熵损失函数(1)下,当先验分布为逆Gamma分布Γ-1(α,λ)时,尺度参数η的Bayes估计为

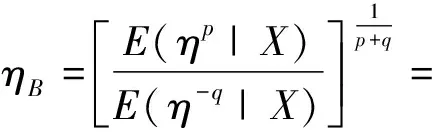
2 尺度参数的经验Bayes估计

经验 Bayes估计[10]是Bayes估计的改进与推广,主要利用历史信息对先验分布或者先验分布的某些数字特征作出直接或间接的估计.

定理3在加权p,q对称熵损失函数(1)下,若Weibull分布(2)的尺度参数η的先验分布为逆Gamma分布Γ-1(α,λ),η的Bayes估计的结果中存在超参数α和λ,当超参数α已知,λ未知时,则η的经验Bayes估计为

证明样本X=(X1,X2,…,Xn)的边缘概率密度函数为

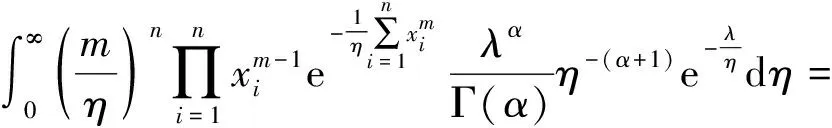
对t(λ|x)取对数,得

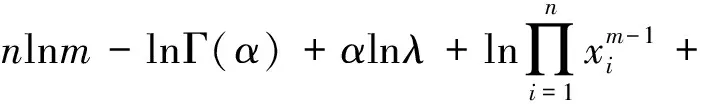
然后关于λ求导令其为0,得

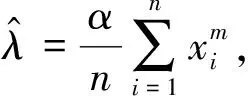
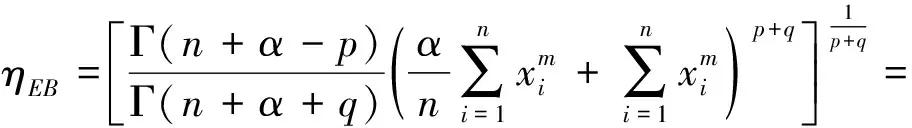
3 数据模拟

为了验证估计的稳健性和精确性,根据上面所得结论,选择真值η=3,m=1,利用R语言编程生成Weibull分布的随机样本.首先选定p=4,q=3,α=3,λ=2,样本容量n为40,60,80,100,120,计算在损失函数(1)下Weibull分布(2)的尺度参数的Bayes估计和经验Bayes估计,运行100次,取平均值,模拟结果如表1和表2所示,其中MSE[11]表示均方误差,Abs[12]表示偏差.

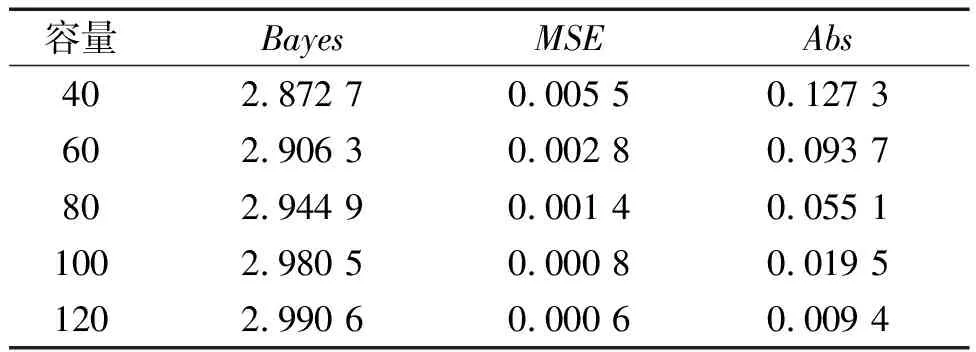
表1 不同样本容量下尺度参数的Bayes估计的模拟结果

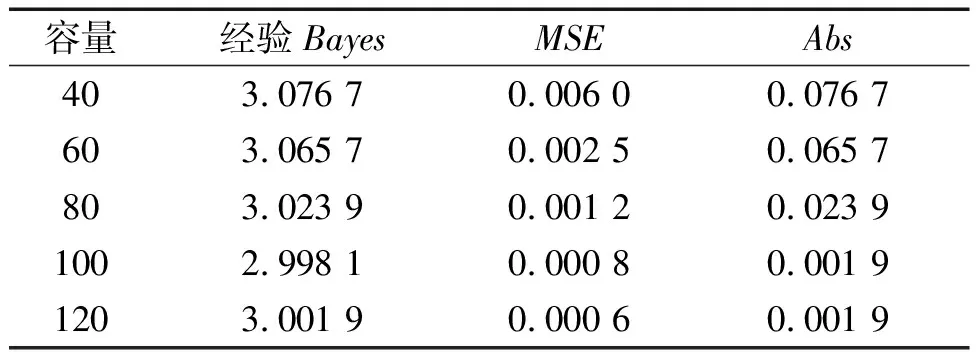
表2 不同样本容量下尺度参数的经验Bayes估计的模拟结果

由表1和表2可知随着样本容量n值的不断增大,在损失函数(1)下Weibull分布(2)尺度参数的Bayes估计值和经验Bayes估计值与真值相差不大,均方误差MSE和偏差Abs较小,模拟效果较好.

下面验证α和λ对Bayes估计和经验Bayes估计的影响,选定α为0.5,1,1.5,2,2.5,λ为0.5,1,1.5,2,2.5,n=100,p=4,q=3,计算尺度参数的Bayes估计和经验Bayes估计,模拟结果如表3和表4所示.

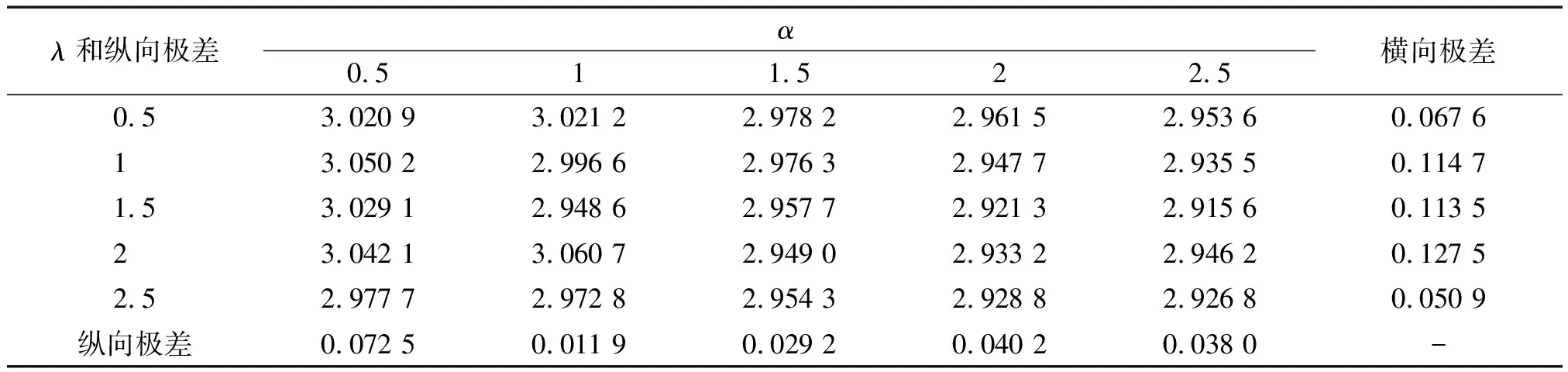
表3 不同α和λ时尺度参数的Bayes估计的模拟结果

表4 不同α时尺度参数的经验Bayes估计的模拟结果

由表3知,尺度参数的Bayes估计值与真值相差不大,模拟效果较好,并且随着参数α和λ的改变,参数的估计值没有太大改变,横向极差和纵向极差不超过0.2,稳健性较好.由表4知,随着参数α的改变,参数的经验Bayes估计与真值相差不大,稳健性较好,精确度较高.

其次,验证p和q对Bayes估计和经验Bayes估计的影响,选择p为1,2,3,4,5,q为1,2,3,4,5,n=100,α=3,λ=2,计算在损失函数(1)下Weibull分布(2)尺度参数的Bayes估计和经验Bayes估计,模拟结果如表5和表6所示.

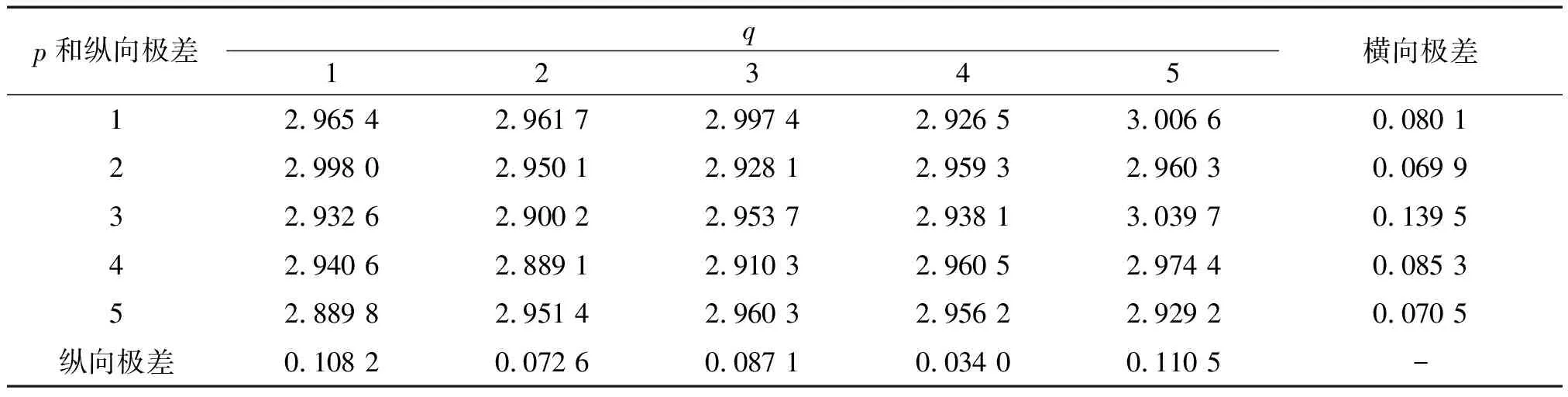
表5 不同p和q时尺度参数的Bayes估计的模拟结果

表6 不同p和q时尺度参数的经验Bayes估计的模拟结果

由表5和表6知,随着参数p和q的改变,尺度参数的Bayes估计值和经验Bayes估计值没有太大变化,横向极差和纵向极差不超过0.2,稳健性较好,精确度较高.

为了更好地比较Bayes估计和经验Bayes估计的精确性,选择α=2,λ=1.5,容量n为100,计算尺度参数的Bayes估计和经验Bayes估计,模拟结果如表7所示.

表7 尺度参数估计的模拟结果

由表7可知,无论从MSE层面还是Abs层面,尺度参数的经验Bayes估计的返真性高于Bayes估计,因此经验Bayes的精确度更高,它可以降低逆Gamma先验分布中的参数对结果造成的影响.

4 结束语

本文在Bayes框架下,使用加权p,q对称熵损失函数,研究了Weibull分布尺度参数的Bayes估计和经验Bayes估计. 首先通过Bayes参数估计方法计算了Weibull分布尺度参数的Bayes估计,其次在所得估计的基础上,给出该分布参数的经验Bayes估计,最后通过数据模拟验证了经验Bayes估计的精确性较高,在一定程度上丰富了Weibull分布在理论上的研究内容.