LNG双液滴蒸发模型及应用

束露露, 费正阳, 邓佳佳

(1.浙江海洋大学 船舶与海运学院，浙江 舟山 316022；2.广西电力职业技术学院，广西 南宁 530007)

0 引 言

为尽快实现“碳达峰”“碳中和”战略目标，国家在各方面均作出相应部署。天然气作为一种优质、易于存储的清洁能源，需求量逐年上升[1-2]。将天然气低温冷却成液化天然气(Liquefied Natural Gas，LNG)是运输、储存效率较高的一种方式，并利于安全使用和环境保护[3]。为防止在预冷过程中因液舱内外温差过大造成安全事故，一般用LNG作为制冷剂对液舱进行喷雾预冷，在预冷前用LNG蒸汽将舱内凝点较高的气体置换出去[4-6]。因此，研究LNG液舱喷雾预冷过程并在工程中的应用十分重要。

LNG液舱在预冷过程中，其起始环境温度远高于饱和温度，传质非常剧烈，高速蒸汽吹拂使边界层加厚，阻碍传热[7-9]，即液滴蒸发产生“吹拂效应”[10-11]。丁继贤等[12]通过建立单液滴蒸发模型，并对其进行数值模拟，得出在高温和强对流环境下增大环境压力可以促进液滴蒸发，而在温度较低的弱对流环境中增大环境压力反而会延缓液滴蒸发。ZHAN等[13]用单液滴干燥(Single Droplet Drying，SDD)装置，模拟脱硫废水液滴在高温气体中的对流蒸发过程，得出液滴蒸发速率随体积温度的升高而升高。随着对液滴的进一步研究，ZHAO等[14-15]将静态液滴相变模型与运动模型相结合，建立单个液滴的运动相变模型。

由于在液舱预冷过程中舱内温度变化幅度较大，且LNG喷淋状态为多液滴并存，而现有的液滴蒸发模型与实际工程应用误差较大，因此建立新计算模型，并对其进行应用模拟。

1 模型建立

对LNG饱和双液滴在其蒸汽中蒸发的过程进行建模，并对网格展开无关性验证。

1.1 假设简化

假设简化条件：①液滴在蒸发过程中维持球形不变；②双液滴的粒径始终相同；③模型中的气体选择甲烷；④由于液滴内部运动对传热与传质产生的影响较小，因此忽略液滴内部运动带来的影响；⑤忽略蒸汽热辐射带来的影响；⑥液滴内部和气液界面处设置为饱和温度。

1.2 数学模型

连续性方程为

(1)

式中：x为径向坐标；ρ为蒸汽密度；vx为轴向速度；r为轴向坐标；vr为径向速度。

动量守恒方程为

(2)

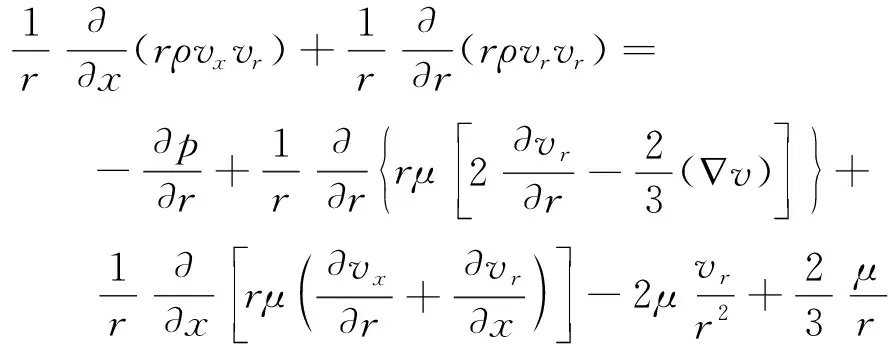
(3)

式(2)和式(3)中：p为压力；μ为黏度；v为来流速度；Fx为浮升力项，Fx=-gαΔT，其中，α为体胀系数，ΔT为温差。

能量守恒方程为

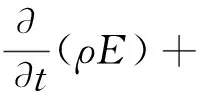
(4)

加入组分方程使液滴能够在混合介质中蒸发模拟。组分扩散方程为

∇(ρvwi)=-∇Ji

(5)

式中：wi为i相的质量分数；Ji为i相的扩散通量。

由气液界面能量守恒定律可知：液滴相变所需的潜热等于蒸汽传递给液滴的热量。液滴表面的蒸汽喷发速度为

(6)

式中：v2为液滴表面蒸汽蒸发速度；q为热流密度；ΔH为液滴蒸发所需的潜热。

选择理想气体模型计算气相介质密度ρ′，即

(7)

式中：pop为操作压力；p1为相对压力；MW为气体介质的相对分子质量；R为普适气体常数。

为了确定上下液滴之间的距离对液滴蒸发的影响，定义无量纲相对距离C：

(8)

式中：S为液滴间距；d为液滴粒径。

1.3 物理模型

由于LNG液滴的喷雾预冷过程是多液滴间相互影响的过程，因此以双液滴为基础，建立上下双液滴二维轴对称物理模型，如图1所示。图2为其网格示例。

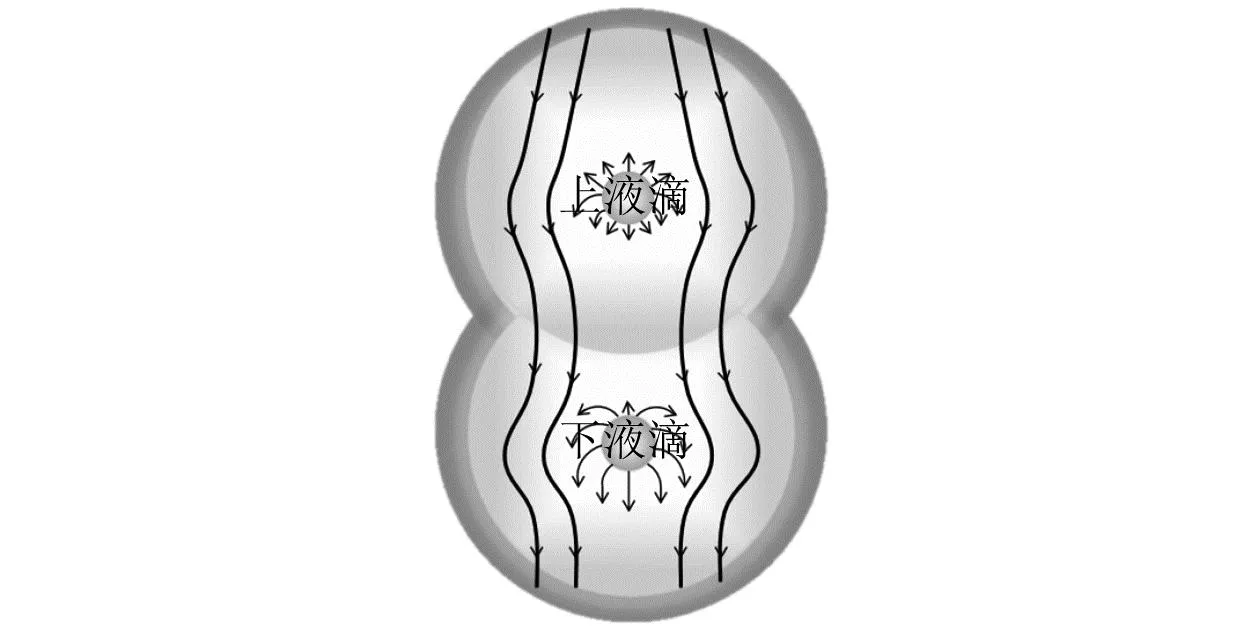
图1 双液滴物理模型

图2 网格示例

2 网格无关性验证

在计算过程中，网格数量对模拟结果的精度具有一定的影响。选择ΔT为190 K、C为30、d=2.5 mm的双液滴模型计算，划分3组不同数量的网格，具体如表1所示。

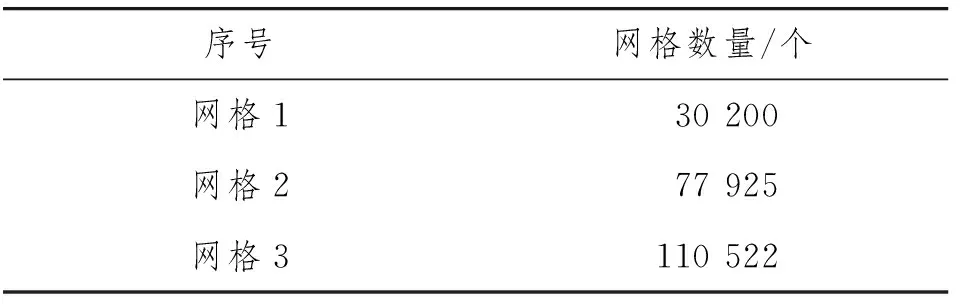
表1 不同数量网格

图3为双液滴在3种网格数量下得到的局部热流密度q随来流夹角φ变化的对比图。由图3可知：网格1不管是上游液滴还是下游液滴的q随φ的变化曲线与网格2和网格3均出现明显分离，而网格2和网格3的曲线基本重合，说明在网格数量为77 925时已满足计算要求，因此为了节约计算成本选用网格2进行后续计算。

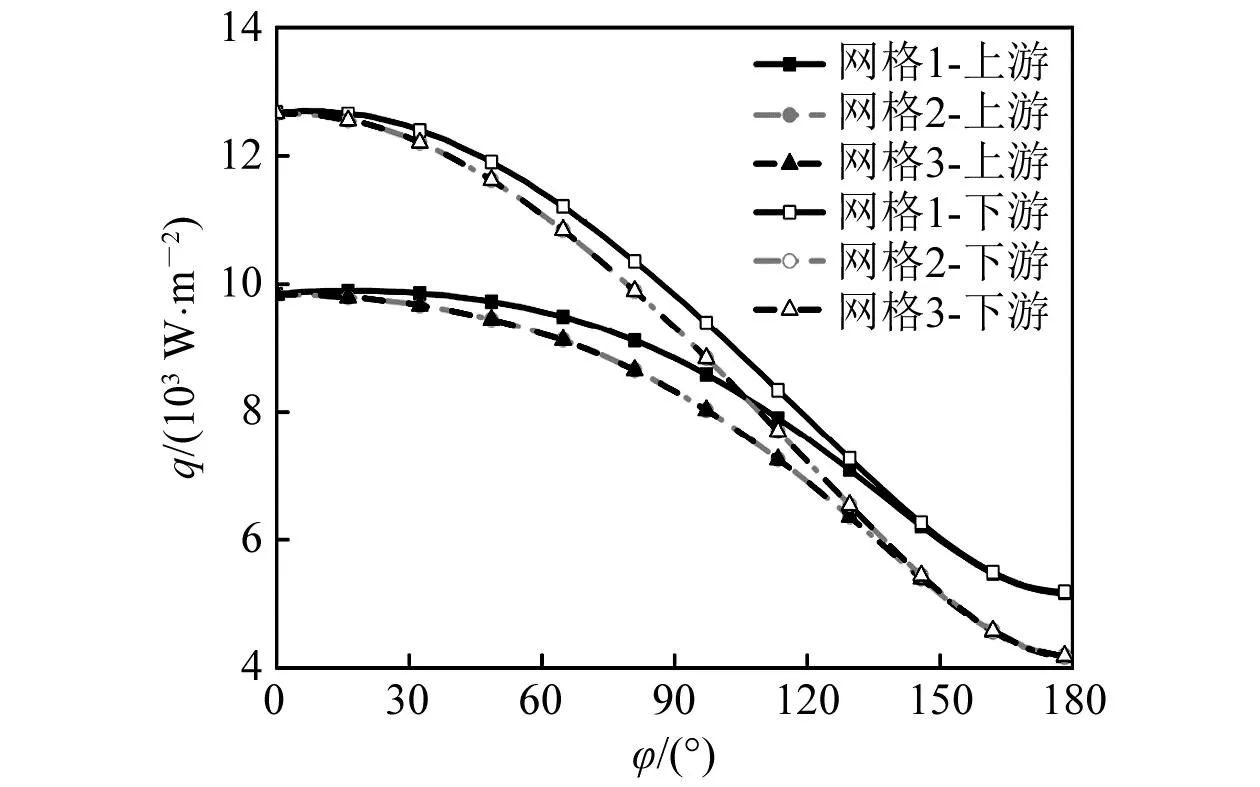
图3 局部热流密度变化曲线

3 液舱预冷应用与分析

为了使所建立的模型能够在工程中实际应用，将双液滴置于一个60.0 mm×60.0 mm×100.0 mm的长方体内，模拟在真实工况条件下液滴的传热与传质过程，进而预测模型的准确性。

3.1 模型设置

图4为模拟的液舱预冷模型网格示例。采用Gambit进行几何建模和网格划分，并对液滴表面进行局部加密处理。模型选用Symmetry对称结构，上液滴中心设置为坐标原点，液滴表面设为速度入口，液舱上顶面设为压力出口，出口温度设为平均温度，其余部分设为液舱壁，z轴负方向添加g=9.81 m/s2。蒸汽起始温度为300 K，液滴表面温度为110 K。使用密度求解器，采用二阶迎风格式离散。

图4 液舱预冷模型网格示例

3.2 液舱预冷过程模拟预测

图5为不同粒径液滴预冷温降曲线对比。由图5可知：液舱内的T在起始50 s内迅速降低，之后随时间的增加缓慢下降。单液滴较双液滴使T的降低速度更缓慢，且单液滴作用下的T大于双液滴。双液滴的C越大，温降速率越大。由图5(a)可知：在d=2.5 mm、C=70、t=300 s时，双液滴作用下的T为95 K。由图5(d)可知：在d=1.0 mm、C=70、t=300 s时，双液滴作用下的T为138 K。随着液舱预冷时间的增大，双液滴作用下的液舱趋于稳定时的T随d的减小而增大。

图5 不同粒径液滴预冷温降曲线对比

图6为粒径对预冷结束时间的影响，其中，单液滴参考文献[16]的研究结果。由图6可知：预冷结束时间随着d的增加而减小，且双液滴的C越大，预冷结束时间越小。在d=2.5 mm工况条件下，单液滴预冷结束时间为333 s，在C分别为10、40、70时的双液滴预冷结束时间分别为299 s、233 s和200 s，双液滴预冷结束时间相比于单液滴分别减少约10%、30%和40%，而C=40的时间相比于C=10缩短约22%，C=70的时间相比于C=40缩短约14%，即双液滴的预冷结束时间小于单液滴，且预冷结束时间随C的增大而减小。在d=2.0 mm工况条件下，单液滴预冷结束时间为438 s，在C分别为10、40、70时的双液滴预冷结束时间分别为394 s、306 s和263 s，双液滴预冷结束时间相比于单液滴分别减少约10 %、30 %和40 %。在d=1.5 mm工况条件下，单液滴预冷结束时间为685 s，在C分别为10、40、70时的双液滴预冷结束时间分别为616 s、480 s和411 s，双液滴预冷结束时间相比于单液滴分别减少约10%、30%和40%。在d=1.0 mm工况条件下，单液滴预冷结束时间为1 552 s，在C分别为10、40、70时的双液滴预冷结束时间分别为1 397 s、1 086 s和931 s，双液滴预冷结束时间相比于单液滴分别减少约10%、30%和40%。因此，无论粒径大小，在C为10、40、70时的双液滴预冷结束时间相比于单液滴均分别减少约10%、30%和40%。

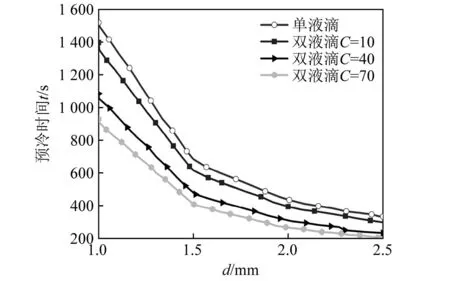
图6 粒径对预冷结束时间的影响

图7为d=2.5 mm工况条件下的液舱起始温度T0对预冷结束时间的影响。由图7可知：单液滴和双液滴的预冷结束时间与T0基本呈线性关系，且随着T0的升高，液滴的预冷结束时间增加。单液滴的预冷结束时间与T0的斜率为1.050 s/K。在C分别为10、40、70时的双液滴预冷结束时间与T0的斜率分别为0.945 s/K、0.735 s/K、0.630 s/K。在T0为220 K时，单液滴的预冷结束时间为249 s，在C分别为10、40、70时的双液滴预冷结束时间分别为224 s、174 s和149 s。

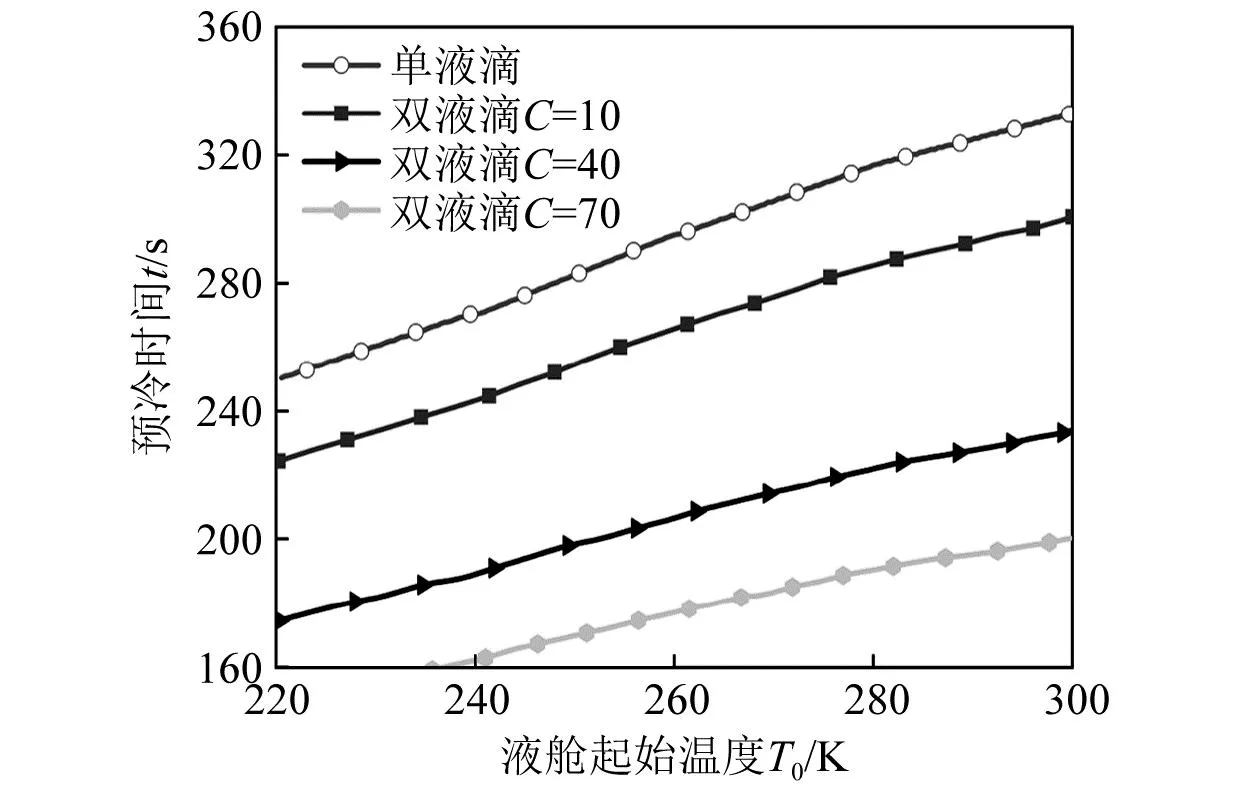
图7 d=2.5 mm工况条件下的液舱起始温度T0对预冷结束时间的影响

4 结 论

运用在不同C条件下的双液滴蒸发模型，建立一个液舱缩尺新模型对预冷过程进行模拟预测，并与单液滴进行对比，得到如下结果：

(1)液舱喷雾预冷时的T在起始阶段下降得较快，随着时间的增加，T的下降速度逐渐变缓，而双液滴的C越大，液舱预冷结束时间越小。

(2)双液滴液舱预冷结束时间与d呈反比关系，与T0呈正比关系。

(3)该新模型以双液滴为基础进行数值模拟研究应用，较常规单液滴模型更进一步接近实际工程应用，具有较高的准确性，从而降低在液舱预冷过程中存在的潜在安全风险，但对于多液滴之间的相互作用方面有待进一步完善。