面向水下焊接电信号的粒子群优化小波软阈值去噪法研究

李康，吕卫文，夏卫生

华中科技大学 材料科学与工程学院 材料成形与模具技术国家重点实验室，湖北 武汉 430074

0 引言

水下焊接技术广泛应用于海洋工程结构的建设和维护，如海洋管道、钻井平台与跨海大桥等［1］。与陆上焊接相比，水下焊接具有条件极为恶劣、焊接热量散失快、水下压力大以及稳定性差等特点。而且在水下焊接视觉质量检测技术中，由于水流导致可见性差，需要架设高速摄像机，实验成本高与难度大。通过实时采集焊接过程的电流与电压信号，开展焊接质量在线评估是一条有效途径［2-3］。而在实际水下焊接过程中，由于水流以及焊接设备电路等噪声因素的干扰，使得所采集的电信号在特征提取和模式识别等存在困难。为此，针对水下焊接电信号进行去噪处理来提取有效的信号特征，对焊接质量在线监测具有重要意义。

小波变换理论具有良好的时频特性，在机械故障诊断、心电信号分析、电力检测等领域广受关注［4-5］。小波去噪方法主要包括模极大值法、小波系数相关法和阈值法等［6］。其中，小波阈值去噪具有易于实现、原始信号特征保留完整等优势，一直是研究的焦点。文献［7］提出了一种经验小波阈值的方法，应用于风机叶片轴承的去除重噪声和提取弱故障信号，具有良好的诊断效果。基于车削振动信号，文献［8］研究了不同阈值函数的原理，提出了一种小波去噪的改进阈值函数，兼具软、硬阈值处理的优点。文献［9］基于VisuShrink阈值开发了一个新的阈值，克服了硬阈值去噪方法的不连续性。文献［10］提出了一种基于蚁群优化小波阈值算法，能有效处理非平稳的变电设备状态信号，降低信号畸变。

本文针对水下焊接电信号，提出一种粒子群优化的小波软阈值去噪算法，选用小波软阈值处理函数结合粒子群优化算法搜索全局最优阈值。为验证算法的去噪效果，采用信噪比和均方根误差作为评价指标，分别进行仿真及实测水下焊接电信号的去噪实验。

1 小波去噪理论

1.1 小波阈值去噪基本理论

通常，叠加高斯白噪声干扰的一维观测信号可以表示为：

式中F（i）为含有噪声的采集信号；f（i）为“纯净”的信号；e（i）为独立同分布的高斯白噪声；ε为噪声水平，信号长度为N。

传统小波分析的基本思想是对信号进行降阶分解，分解成近似分量和细节分量。其中，近似分量主要为低频信号，表示信号的有用部分；细节分量主要为高频部分，表示信号的噪声部分。而小波阈值去噪实质就是保留有用部分，抑制噪声信号。其基本流程如图1所示。

图1 小波阈值去噪流程Fig.1 Flowchart of wavelet threshold denoising

图1中小波阈值去噪的主要流程包括：（1）小波分解：选择合适的小波基和分解尺度，对噪声信号进行离散小波分解，获得一组小波系数ωj，k。（2）阈值处理：对分解的各层系数分别进行阈值λ量化处理，进而获得一组估计的小波系数。（3）小波重构：基于估计的小波系数，通过小波逆变换进行信号重构，获得去噪后的信号（i）。

1.2 去噪评价

对于不同的去噪方法，需要一定的评价指标衡量算法的优劣。常用的评价指标有：信噪比（Signal Noise Ratio，SNR）、峰值信噪比、均方根误差（Root Mean Square Error，RMSE）、归一化均方误差以及平滑度等［11］。其中，信噪比、峰值信噪比等反映算法对噪声的抑制能力，值越大，算法性能越优；均方根误差、归一化均方误差等反映算法对原始信号的破坏程度，值越小，算法性能越优；平滑度反映去噪后信号的平滑程度，值越小，算法性能越优，但是并不适用于相对高频、非稳态的焊接电信号的评价［12］。这些评价指标分别从不同维度反映了算法的去噪能力。综上，本文选取了常用的信噪比SNR和均方根误差RMSE作为去噪评价指标，其中：

（1）信噪比SNR。信噪比的定义为原始信号的平均功率和噪声的平均功率之比，记作SNR或S/R，单位为dB。信号的信噪比反映了对噪声的抑制能力，值越大，说明噪声在信号中占比越小，去噪效果越优。其计算公式为：

式中F(i)为原始含噪信号；为去噪后的信号；N为信号长度。

（2）均方根误差RMSE。均方根误差是指原始信号和去噪后信号之间方差的平方根，反映了对原始信号的破坏程度。一般来说，值越小，对原始信号损伤更小，去噪效果越优。其计算公式为：

2 基于粒子群优化的小波软阈值方法

2.1 粒子群优化小波软阈值原理

由于实际水下焊接电信号属于非平稳信号，采用一般小波阈值算法去噪时，难以获得理想的结果，容易出现阈值选取不当，高频信号被误当作噪声处理。因此，本文通过引入粒子群优化算法（Particle Swarm Optimization，PSO），以目标函数—SNR作为评价指标，快速进行全局搜索最优阈值。

粒子群优化算法是一种发展于计算机智能领域的启发式搜索算法［13］。算法基本思想是个体和群体共享速度和位置，基于不断迭代，搜索获得全局最优值。由于粒子群算法原理简单易实现，且参数较少，因此在函数优化、机器学习模型调优、图像处理等领域应用广泛。PSO算法的基本原理为［14］：

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落：其中，第i个粒子的位置用D维的向量表示为：Xi=（xi1，xi2，…，xiD），初始运动速度用D维的向量表示为：Vi=（vi1，vi2，…，viD），其中i=1，2，…，N。在每次迭代过程中，第i个粒子的最优位置，即个体局部位置最优为：pbest=（pi1，pi2，…，piD）；整个粒子群中，搜索到的最优位置，即全局位置最优为：gbest=（pg1，pg2，…，pgD），其中i=1，2，…，N。

因此，从第t代迭代到第t+1代，粒子的速度vij（t+1）由当前速度、局部最优值、全局最优值三部分共同更新：

同时，粒子的位置xij（t+1）更新为：

式中ω表示粒子的惯性因子，反映粒子的全局搜索能力；c1和c2分别为个体学习因子和群体学习因子，也被称作加速度常数；r1（t）和r2（t）是在［0，1］分布的随机数。

2.2 算法实现

PSO小波软阈值去噪算法的基本步骤为：（1）设定PSO的基本参数：惯性因子ω，粒子群数目N，最大进化代数MaxIt、权重系数ω，粒子的最大速度Vmax；（2）初始化粒子群：随机生成N个初始值，包括每个粒子的速度、位置；（3）以SNR作为目标函数：作为评价每个粒子的适应度值，SNR值越大，适应度越好；（4）更新粒子的局部、全局最优值：通过比较每个粒子的当前最优值和pbest，更新pbest；同理，更新全局最优值gbest；（5）根据式（4）和式（5）更新粒子的速度和位置。对于粒子的速度，若Vi＞Vmax，则Vi=-Vmax；（6）判断PSO算法是否满足迭代条件：如果满足，输出全局最优值SNRbest；否则，转入步骤（3），进入下一步循环迭代。

本文PSO算法的相关参数设定为：粒子群种群大小N=50；最大迭代次数MaxIt=50；惯性因子ω=1；c1和c2两个学习因子，通常设置c2=c2=2。将PSO小波软阈值算法应用于去除水下焊接电信号中的白噪声，其算法流程如图2所示。

图2 PSO小波软阈值算法的去噪流程Fig.2 Flowchart of denoising by PSO wavelet soft thresholding algorithm

3 仿真水下焊接电信号的去噪分析

3.1 信号构造

在实际水下焊接实验中，传感器采集的信号除正常焊接信号外，必然还掺杂大量噪声信号。为验证算法的可行性和有效性，首先构造一个典型的焊接过程仿真电压信号，信号的采样频率为10 kHz，样本数目为20 k，如图3a所示。同时，加入dB=20，服从正态分布的高斯白噪声以模拟干扰噪声，从而所构造的染噪信号如图3b所示。

图3 水下焊接的仿真信号Fig.3 Simulated signals of underwater welding

3.2 去噪效果分析

采用MATLAB作为仿真工具，选用极大极小阈值、启发式阈值、RSURE阈值以及本文提出的PSO小波软阈值算法，分别对仿真的水下焊接染噪信号进行去噪处理。其中，仿真实验的小波基采用sym13小波，分解层数为3层。图4给出了各算法去噪效果。

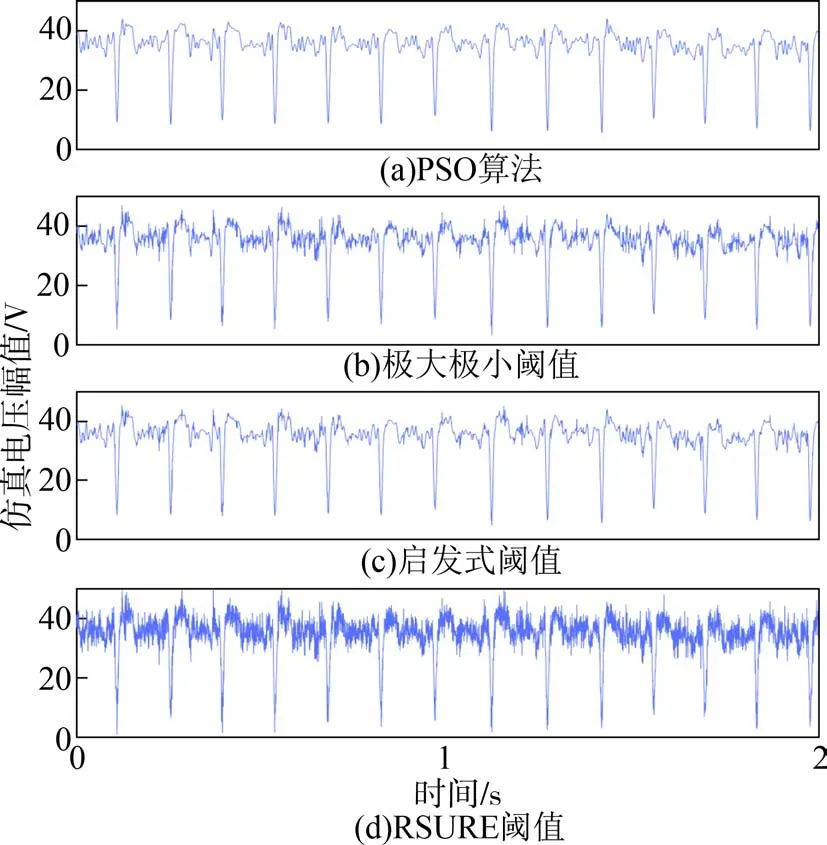
图4 当信噪比为20时各处理算法的去噪效果Fig.4 De-noising results of each processing algorithm under SNR=20

如图4所示，PSO小波软阈值算法和启发阈值方法都能有效去除白噪声干扰，保持一定的信噪比，保留了原始信号的特征，而RSURE阈值方法在去噪效果上较差。

为进一步测试本文所去噪算法的性能，对仿真信号分别加入不同信噪比（dB=8、10、13、15、18、20）的高斯白噪声，经四种去噪方法处理，分别采用信噪比SNR和均方根误差RMSE评价去噪效果，如图5所示。根据图4的去噪效果波形图（SNR=20），结合图5去噪效果评价，对比四种算法的去噪效果，可以得出：

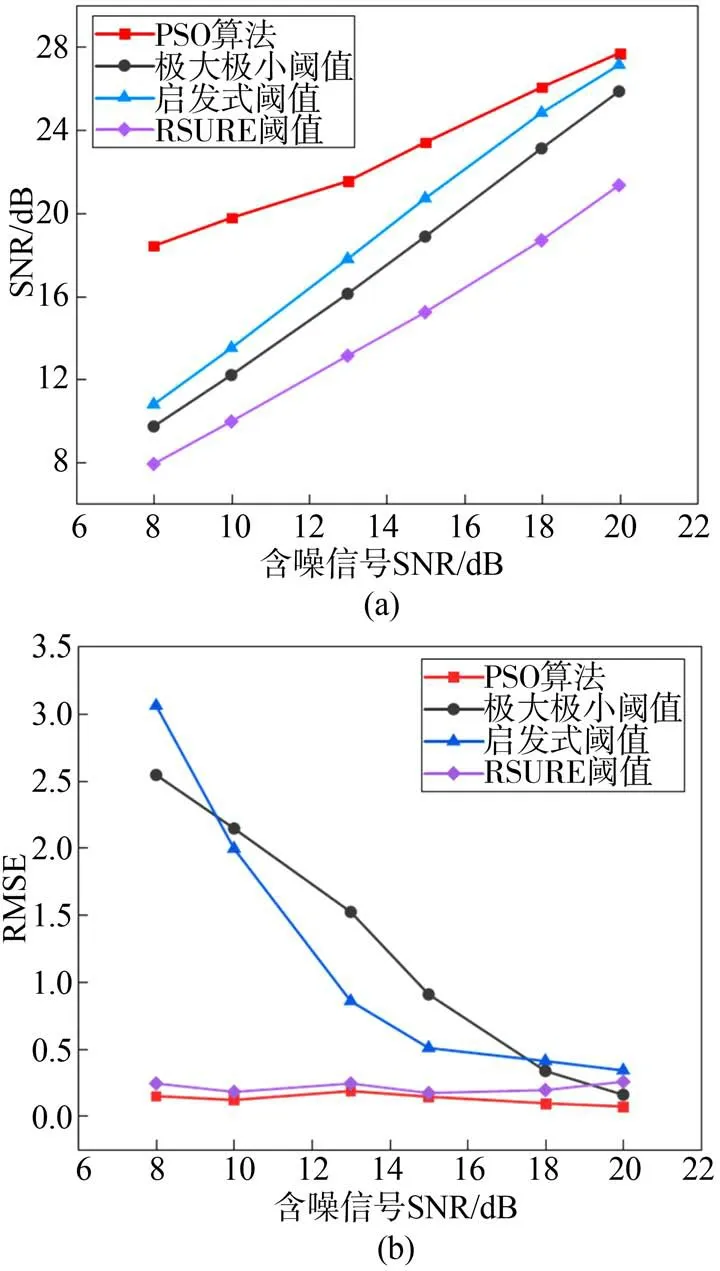
图5 加入不同信噪比白噪声后各算法的去噪效果对比Fig.5 The de-noising results of each algorithm for different SNRs of white noises

（1）如图4b和图5所示，信号通过极大极小阈值方法处理后，信号的SNR和RMSE结果都比较一般，去噪重构后信号整体较粗糙；如图4c所示，信号通过启发式阈值方法处理后，有良好的去噪效果，但RMSE值较大，这说明对原始信号损伤较大，信号的局部特征保留不完整，局部较粗糙；如图4d所示，信号通过RSURE阈值方法处理后，虽然RMSE较小，但整体去噪效果最差。

（2）本文提出的PSO小波软阈值算法的SNR更大，RMSE最小，噪声能被较好地滤除的同时，保留信号细节特征。

4 实际水下焊接电信号的去噪分析

开展水下湿法药芯焊接实验，通过霍尔传感器采集焊接过程电信号，采样频率为10 kHz。每个电信号样本长度为2 s，共计20k个数据点。图6为一个包含背景干扰噪声的水下焊接过程的实测电信号。图7是分别采用本文提出的PSO小波软阈值算法、极大极小阈值、启发式阈值以及RSURE阈值方法的去噪结果。为体现去噪细节信息，对0.7～1.0 s的局部去噪信号进行放大对比。相关的去噪效果特征值对比见表1。

表1 实测水下焊接电信号的去噪效果特征值对比Table 1 Eigenvalue comparison of de-noising results with the measured welding electrical signals

图6 实测水下焊接电信号Fig.6 Measured electrical signals of underwater welding

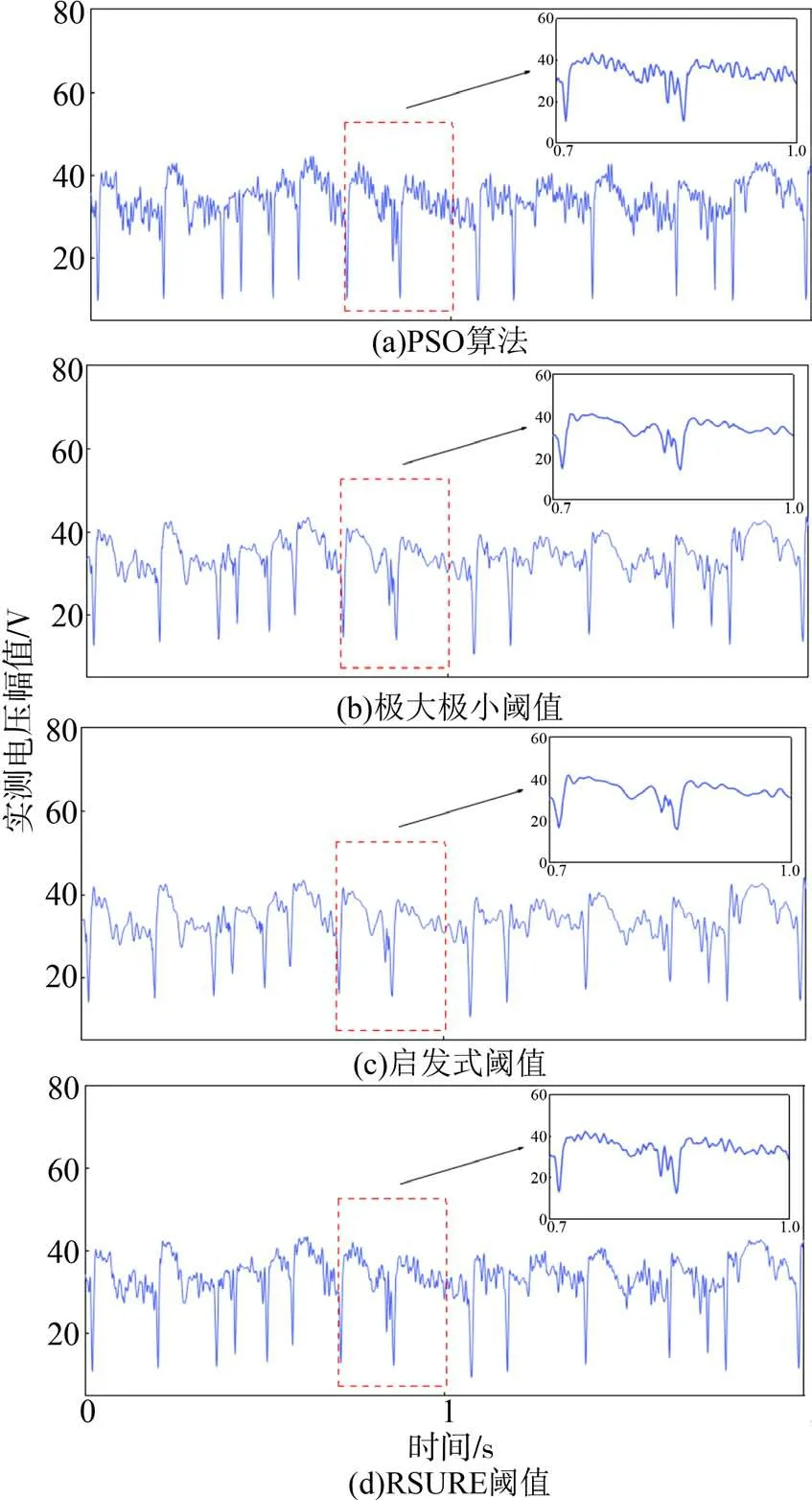
图7 实测水下焊接电信号的去噪效果Fig.7 The denoising results of electrical signals with measured underwater welding

由图7与表1可知，极大极小阈值和启发式阈值在局部细节上处理并不理想，波形的细节受到严重丢失，被过度的平滑，信号的细节特征会丢失；RSURE阈值的处理效果一般，波形细节也有一定的畸变。本文所提出的PSO小波软阈值算法处理后，信号的SNR更大，RMSE更小，在滤除噪声的同时能极大地保证波形的完整性与细节信息，整体去噪效果最好。

5 结论

本文针对水下焊接电信号提出了一种粒子群优化的小波软阈值去噪算法，并与极大极小阈值、启发式阈值以及RSURE阈值方法进行对比来验证所提算法的去噪效果。主要结论包括：

（1）针对染噪的仿真水下焊接过程电信号去噪分析，提出的粒子群优化小波软阈值算法能有效去除白噪声干扰，还原信号特征，减少原始信号畸变。

（2）针对实测水下焊接电信号去噪分析，经粒子群优化小波软阈值算法处理后，信噪比更高、均方根误差更小，且能有效保留信号的细节信息。