基于三元闭包模体的关键节点识别方法

徐 越,刘雪明

(华中科技大学人工智能与自动化学院,武汉 430074)

0 引言

复杂网络能够描述许多真实系统,如社交网络、贸易网络和交通运输网络等,网络中的关键节点与其结构稳定性和系统功能紧密相关[1]。对于关键节点的识别,能够为提高系统的鲁棒性和效率提供针对性建议[2]。例如,在社交网络中,识别出关键用户,能够控制社交信息的交互和传递,从而有效控制网络舆情。在贸易网络中,关键节点的识别能够确定贸易枢纽,对于维持贸易网络的稳定性以及提高贸易效率具有重要意义。在交通运输网络中,关键节点能够影响网络的整体连通性。在经受自然灾害等破坏时,对于关键节点的维护,能够有效保障交通运输网络的顺畅运行。

现阶段有多种关键节点的识别方法。节点的中心性指标,例如度中心性[3]、介数中心性[4]等,是识别关键节点的经典方法。K-shell[5]方法采用逐层分离节点的方式,获取网络中的关键节点。WL[6]方法考虑了节点自身的度和邻居节点的度,认为邻居节点的度越大,节点越重要。映射熵ME[7]方法进一步考虑了邻居节点的影响,通过节点与所有邻居节点的连接情况来评估其重要度。

模体作为一种局部统计显著的特征子图,存在于许多真实网络中,能够有效反映网络的整体功能[8-9]。在大肠杆菌转录调控网络中,每种类型的模体都与特定的基因表达功能紧密相关[10]。在动物社交网络中,模体能够反映动物群体的支配层次结构模式,从而揭示社会秩序的形成过程[11]。在有向生物网络中,能够根据节点在不同类型的模体中出现的次数,来衡量该节点的重要度[12]。

进一步的研究表明,三元闭包模体与网络的异质性以及社团的形成紧密相关[13-15]。许多真实网络中的三元闭包模体数目具有显著性[16]。现有研究还未能考虑三元闭包模体的存在与节点重要度间的关系。本文引入了三元闭包模体权重的概念,以此来衡量该模体在网络中的重要度,并提出了一种结合节点度中心性及其所在三元闭包模体权重的关键节点识别方法。以网络最大连通子图的比例以及全局效率作为评价指标,在6个真实网络中进行了鲁棒性实验。同时,利用传播模型SIR对多种节点排序结果进行评价。实验结果表明,本文提出的方法相比于度中心性DC、K-shell分解、WL中心性、映射熵ME方法,能够更加准确地识别出关键节点。

1 基于三元闭包模体的算法

定义无向无权网络G=(V,E),其中V为网络的节点集,E为网络的边集。图1a展示了网络中三元闭包模体的示意图,该结构具有3个节点,节点之间具有强联系,彼此之间有边直接相连。三元闭包模体中的任意两节点间,都有两条较短的独立路径,兼具鲁棒性和高效性。如图1b所示,在相同节点数和边数情况下,相比于四元闭包模体,三元闭包模体结构异质性更强,对该结构中关键节点的破坏,能够对网络的连通性和效率产生较大影响。

图1 三元闭包模体示例

各个三元闭包模体对网络拓扑连通性的影响不同。节点的重要度不仅与本身的度中心性有关,同时还与其所在的三元闭包模体有关。如图1c所示,节点3和节点5具有相同的度中心性,所属三元闭包模体的数目都为1,但对应三元闭包模体的拓扑位置不同。按度选择节点来对网络进行攻击时,4个节点没有区分度。若删除节点3及其连边,网络中剩余最大连通子图的大小为6。若删除节点5及其连边,网络中剩余最大连通子图的大小为5。类似节点度的定义,本文提出了三元闭包模体权重T(j)的概念,即取模体中所有节点度的均值,具体表示为

(1)

其中,n为属于该三元闭包模体T的节点,kn为节点n的度中心性。

结合节点的度和其所在的三元闭包模体权重T(j),本文提出了一种基于三元闭包模体的节点重要度评估方法NT,可以表示为

(2)

其中,ki为节点i的度中心性,T(j)为节点i所在的三元闭包模体的权重,且节点i是该模体中度最大的节点。以图1c为例,节点3的重要度为NT(3)=3+1/3×(2+2+3)=5.33,节点5的重要度为NT(5)=3+1/3×(2+3+3)=5.67,因此节点5比节点3更重要,这与移除节点5对网络造成的破坏性更大的事实一致。

2 对比算法及评价指标

2.1 对比算法

1)度中心性。度中心性通过统计节点的连接数来衡量节点的重要度。在无权无向网络中,可以表示为

(3)

其中,N为网络的节点数,eij为节点i和节点j之间的连接关系,若有连接则eij为1,否则为0。

2)K-shell分解法。K-shell采用逐层分离节点的方式,对节点进行粗粒化分类。该算法首先迭代删除最外层度为1的节点和它的连边,包括新产生的度为1的节点,直到剩余节点的度都大于1。这些被删去的节点和它们的连边是网络的1-shell,即k=1。利用同样的方式,依次删除度为2,3,…的节点,对网络中的节点进行分类,所在K壳越大的节点越重要。

3)WL中心性。WL中心性方法认为节点所连边越重要,则该节点越重要。首先定义了边的权重,表示为

wij=ki×kj

(4)

其中,wij为节点i和节点j之间连边的权重,ki为节点i的度。节点i的重要度取决于其所有连边的权重,可以定义为

(5)

其中,Γi为节点i的邻居节点集。

4)映射熵ME。映射熵方法考虑了该节点所有邻居节点的度,采用类似信息熵的方式来衡量节点的重要度,具体表示为

(6)

其中,DCi为节点i的度中心性,Γi为节点i的邻居节点集,DCj为邻居节点j的度中心性。映射熵值越大的节点越不重要。

2.2 评价标准

目前评价关键节点识别方法的标准主要有两类:一种是根据节点排序结果,依次攻击网络中的节点,评估节点对网络结构和功能鲁棒性的影响[17]。节点移除后对网络造成的破坏程度越大,则该节点越重要。具体来说,可以通过衡量剩余网络中最大连通子图的比例[18],或者网络的全局效率变化[19]来衡量节点对网络鲁棒性的影响。另一种是基于传播模型SIR,选取不同排序结果的关键节点,通过信息传播的方式,来衡量节点集合对网络的影响程度[20],并以此验证关键节点识别方法的有效性[21]。

2.2.1 鲁棒性分析

1)最大连通子图比例。网络中的最大连通子图与网络功能紧密相关[22],连通子图中任意两节点间至少有一条路径。对网络中的关键节点进行蓄意攻击后,会使得网络碎片化,其最大连通子图的大小也会发生变化[23]。最大连通子图比例定义为

(7)

其中,S为删除一定比例节点后,剩余网络中最大连通子图的大小,N为原始网络的节点个数。依次移除节点,最大连通子图比例下降越快,说明关键节点识别方法越有效。通常用最大连通子图比例变化曲线下的面积,来量化关键节点识别方法的有效性。曲线下的面积越小,对应的关键节点识别方法越有效。

2)网络全局效率。网络的全局效率能够衡量节点间信息交换的情况[24],与节点间的最短路径长度有关。移除网络中的关键节点,会造成节点间最短路径长度增加,使网络的全局效率下降[25]。网络全局效率定义为

(8)

其中,N为网络的节点数,dij为节点i和节点j之间最短路径的长度,V为网络的节点集。依次移除节点,网络全局效率变化越快,说明关键节点识别方法越有效。

2.2.2 传播效果分析

SIR是经典的传染病模型,将节点分为易感染节点S、已感染节点I、免疫节点R[26]。已感染节点I会以β的概率感染易感染节点S,同时以γ的概率恢复为免疫节点R。免疫节点R不会再次被感染。网络的传播率阈值[27]可以表示为

(9)

其中,〈k〉为网络的平均度,〈k2〉为网络的二阶平均度。

通过SIR模型可以衡量关键节点的传播影响。选择top-k节点集合,经过t次迭代实验后,通过统计网络中所有感染节点I以及免疫节点R的数量来衡量该集合的传播影响力[28],影响力越大说明这些节点越重要,具体表示为

(10)

其中,t为迭代次数,k为所选择的初始感染节点数目,NI,NR,N分别为t次迭代后网络中已感染节点I、免疫节点R和整个网络的数目。

3 实验结果

3.1 实验数据集

为了验证NT方法的有效性,在6个真实网络数据集上进行了相关实验。6个真实网络的数据集分别为海豚网络Dolphins、爵士音乐家合作网络Jazz、野鸟网络Wildbird、加州理工网络Caltech、社交网络Reed和友谊网络Friendships,这些数据集都来源于公开的网络数据库[29]。

本文验证了真实网络中三元闭包模体数目的显著性。首先计算了统计量指标z,再通过p值检验了其显著性水平。指标z衡量了该模体在随机网络和真实网络上出现数目的差异情况,计算公式:

(11)

其中,|Treal|和|Trandom|分别为真实网络和随机网络中三元闭包模体的数目,后者取100个具有相同节点数和平均度的随机小世界网络的平均值。std(|Trandom|)为三元闭包模体在所有随机网络出现数目的标准差。通过假设检验的方式,定义原假设为:真实网络所对应的统计量z小于或等于随机网络所对应的统计量z′。总体分布视为正态分布,计算得到p值。若概率较小(p≪0.001),则说明该事件具有统计显著性。

表1展示了6个真实网络的拓扑特征。其中N,M分别为网络的节点数和边数,βth为网络的传播率阈值,指标p和z用于评估三元闭包模体数目的统计显著性[8]。结果表明,在6个真实网络中,三元闭包模体的数目都具有统计显著性。

表1 六个真实网络的拓扑特征

3.2 实验结果分析

3.2.1 鲁棒性分析结果

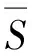
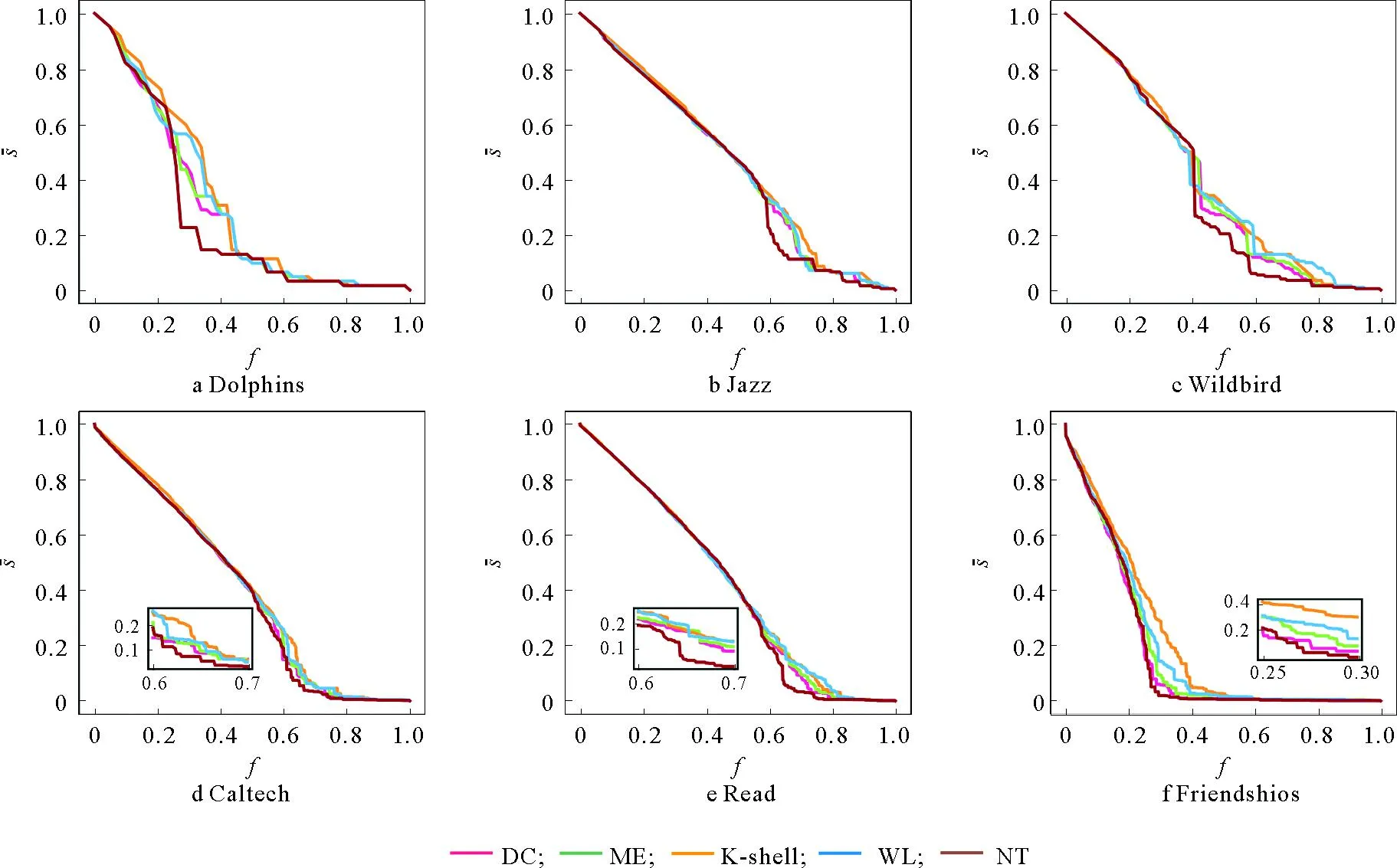
图2 不同攻击条件下,网络最大连通子图比例变化情况

相比于其他方法,根据NT方法对节点的排序结果依次删除节点,能使网络中最大连通子图比例更快下降。尤其在Dolphins和Wildbird网络中,根据NT方法对关键节点的攻击,出现了一阶相变现象。这说明NT方法能够有效评估节点的重要度,并识别出关键节点,删除这些节点能使网络碎片化,从而造成较大程度的破坏。

为量化关键节点识别方法的优劣,计算了网络中最大连通子图变化情况曲线下的面积,结果如表2所示。由表2可知,相比于其他方法,本文提出的关键节点识别方法,能够使网络最大连通子图变化情况曲线下的面积最小,即能够有效识别关键节点,进而破坏网络的连通性。

表2 不同攻击条件下,最大连通子图变化情况曲线下的面积

网络结构的破坏会阻碍节点间的通信,即影响网络的全局效率。在6个真实网络中,根据不同的节点排序结果,从网络中依次删除节点和它的连边,并计算网络全局效率的下降情况。考虑到计算效率,这里采用依次删除1%比例节点的方式进行实验。

实验结果如图3所示,其中横坐标f表示网络中移除节点的比例,纵坐标η表示剩余网络的全局效率。相比于其他方法,根据NT方法对节点的排序结果依次删除节点,能更快地造成网络全局效率的下降。这说明NT方法对关键节点的识别更有效,对这些关键节点的攻击能有效破坏网络的整体功能。

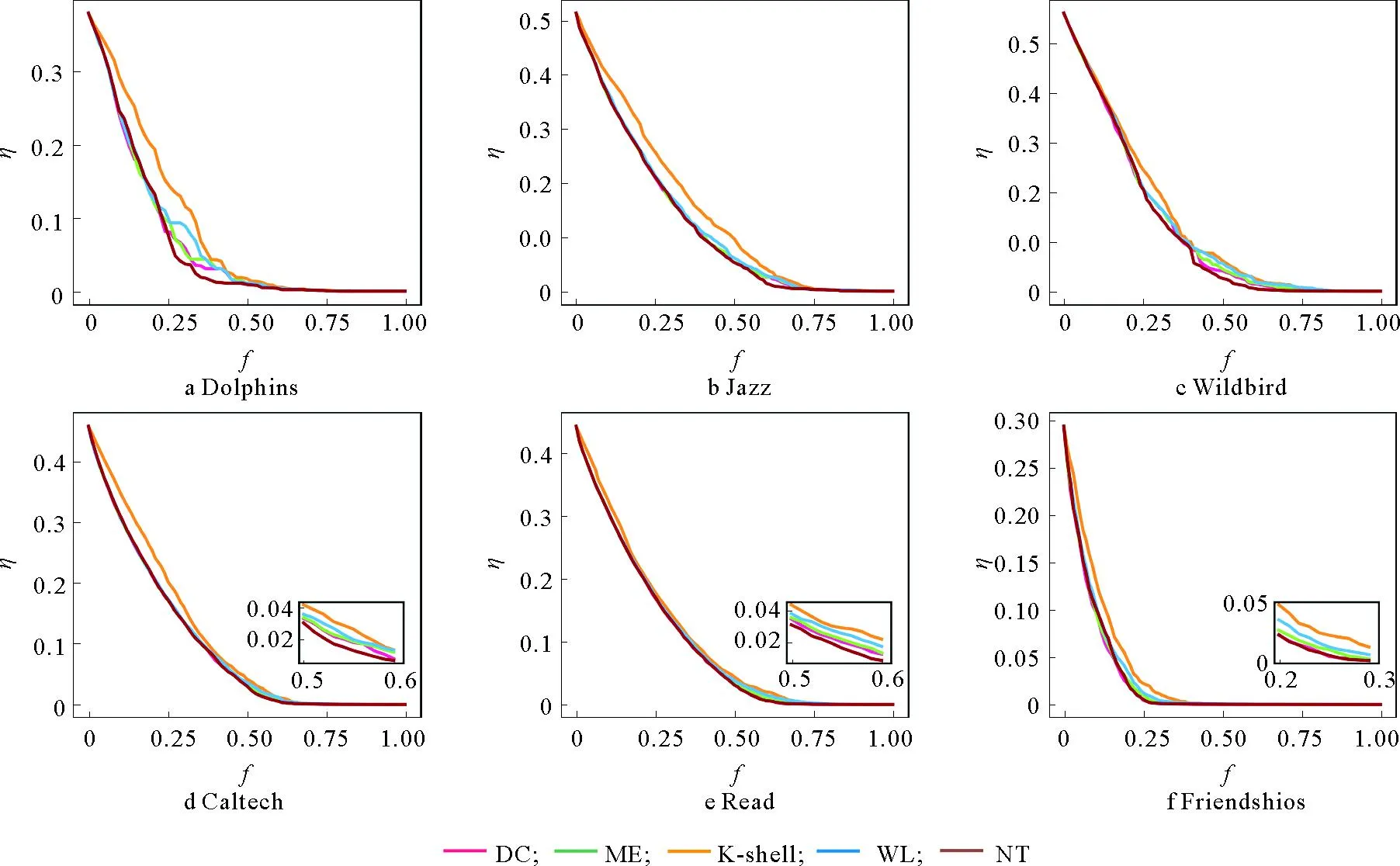
图3 不同攻击条件下,网络全局效率变化情况

3.2.2 传播效果分析结果

为了进一步分析NT方法对网络中关键节点的识别效果,选取了不同排序结果的top-k节点集作为初始感染节点集,在SIR模型上进行了传播实验。本文中迭代次数t取25,初始感染节点数目k取5,β取各个网络的传播率阈值。为了保证结果的可靠性,传播结果取100次实验的均值。实验结果如图4所示,其中横坐标t表示传播的迭代次数,纵坐标St表示网络中感染节点的比例。

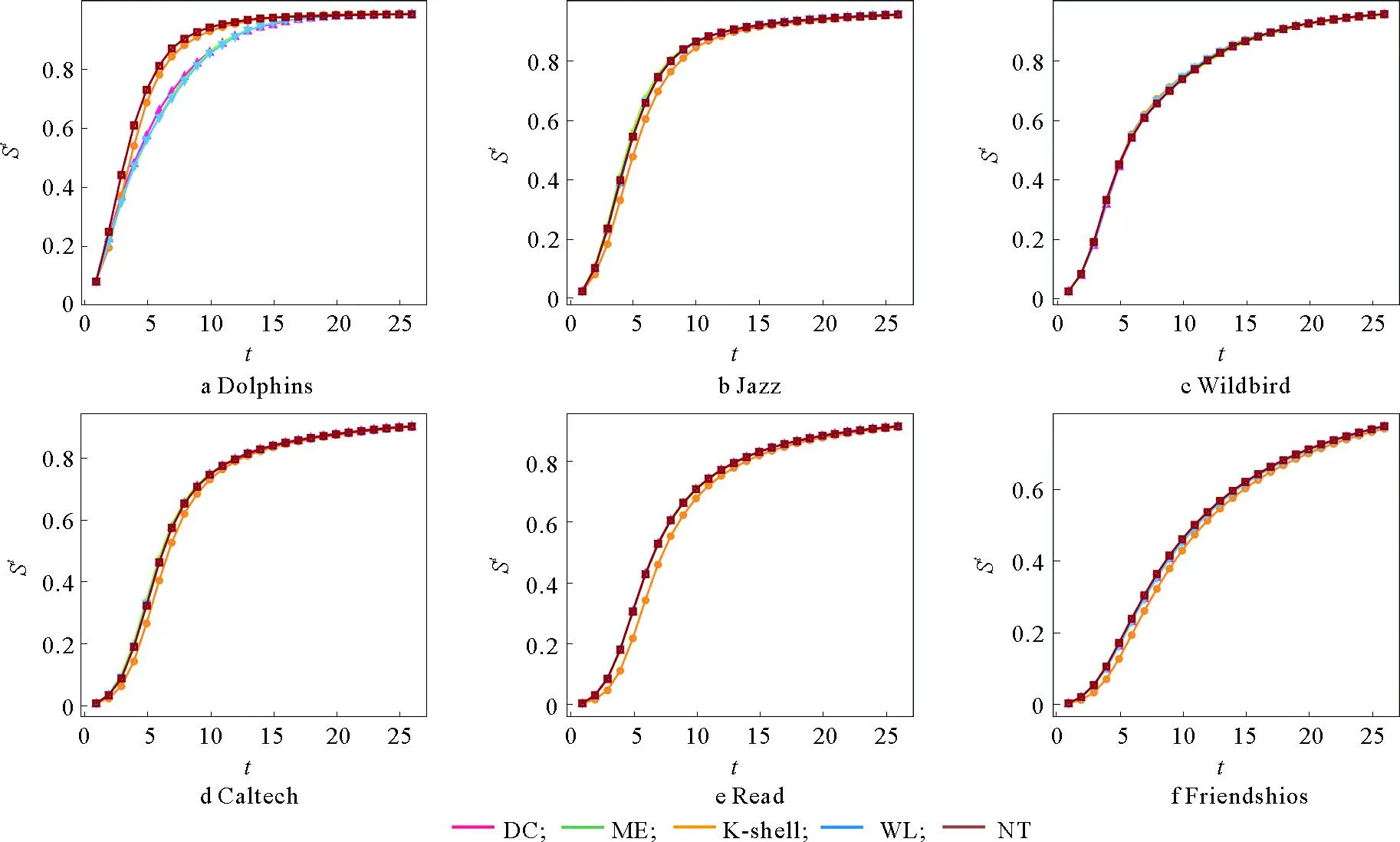
图4 不同条件下,网络中感染节点比例随迭代次数的变化情况

相比于其他方法,NT方法识别出的关键节点集合,能够更快地感染整个网络。这种现象在Dolphins网络中尤其显著,NT方法选择的关键节点能够更有效地传播信息。在其余5种网络中,NT方法的识别效果没有明显优势,但效果也接近于最优的方法。

实验结果说明在6个真实网络中,NT方法对网络关键节点的识别效果优于K-shell方法,这可能与K-shell方法对网络关键节点的识别过于粗粒化有关。整体来说,本文提出的NT方法能够通过节点所在的三元闭包模体及其本身的度中心性来评估节点的重要度,有效识别出关键节点,这些关键节点对网络具有较大的影响力。

4 结论

复杂网络中关键节点的识别,有利于维护网络结构鲁棒性和保障网络功能。本文提出了一种基于三元闭包模体的关键节点识别方法NT,该方法结合了三元闭包模体权重和节点度,来评估节点的重要度,为网络关键节点的识别提供了新思路。在6个真实网络中,进行了鲁棒性实验和SIR传播模型实验。对比于度中心性DC、K-shell分解、WL中心性、映射熵ME方法,NT方法更能有效地识别出关键节点,移除这些关键节点,对网络造成的破坏更大。同时,这些关键节点具有更大的影响力,能够更快地将信息传播到网络中的其他节点。该算法主要适用于无向无权网络,在有向、有权网络上,如何结合网络中的三元闭包模体,对关键节点进行识别,是下一步的研究方向。