展示网络重叠社团结构的可视化布局算法

张铭娜,肖 婧,许小可,2

(1.大连民族大学信息与通信工程学院,辽宁 大连 116600; 2.北京师范大学 a.计算传播学研究中心,广东 珠海 519085; b.新闻传播学院,北京 100875)

0 引言

网络可视化技术以图形化的方式展示了网络数据,直观地呈现出网络拓扑结构信息。网络布局算法是网络可视化的基础,主要通过节点之间的相互作用力更新节点位置,实现网络绘制。最早的布局方法是Eades[1]提出的弹簧布局算法,把网络图形当做物理系统,节点在弹簧弹力的作用下使钢环运动,当弹簧的系统能量达到最小时停止移动,但是他的算法没有遵循胡克定律,而且效率较低。随后Kamada和Kawai对弹簧布局进行了改进,提出了KK算法[2],通过求能量最小值确定节点位置,该算法遵循了胡克定律的偏微分方程,提高了算法效率。Frechterman和Reingold[3]提出了FR布局算法,计算相邻节点之间的吸引力,以及所有节点之间的排斥力,节点在两者合力下更新位置。力导引布局算法易于理解、容易实现、实用性强,是目前最常用的布局算法,但是不利于用户发现社团信息和网络特征。

社团结构是复杂网络的一个重要拓扑结构,即同一社团节点之间高度互连,不同社团节点之间连接密度较低[4]。通过对社团结构进行聚类布局,可以使呈现出的社团结构具有对称性和局部聚合性[5-6]。Nocak[7]提出了Linlog算法,通过计算最小能量来呈现社团结构,虽然达到聚类效果,但是无法验证社团划分结果的有效性。鉴于此缺点,朱志良等[8]将社团抽象为节点,并填充社团内部节点进行网络布局。吴渝等[9]提出社团引力导引的布局算法,在FR算法的基础上加入社团引力,结合k-means[10]算法通过社团引力和斥力更新节点位置,采用边聚类边布局的方式加快了收敛速度。Zhou等[11]在已知社团划分结果的基础上计算社团引力和斥力,进行节点聚类,进而清晰地呈现网络的社团结构。Huang等[12]通过加权排斥力和吸引力对节点位置进行收敛。但是这些社团布局算法主要针对离散社团进行布局,而无法对重叠社团进行可视化呈现。

重叠社团是社团结构的一种特殊形式,对分析网络重要节点在属性上的多重性特征,理解重叠节点与社团之间的归属性,研究社团功能相似性及差异性等具有重要意义[13-14]。由于重叠节点与多个社团相互关联,使得拓扑结构变得复杂,如何从中高效解读和识别重叠节点信息成为人们研究的热点。Vehlow等[15]通过层次网络布局,展示出重叠社团结构,利用视觉映射对重叠社团结构进行编码,但是忽视了社团内部的拓扑结构。针对这一问题,本文先通过重叠社团划分算法对网络进行划分,然后对其硬划分并根据隶属矩阵加权求和确定节点位置,最后对重叠节点进行精确布局,通过饼图颜色分配量化节点信息,实现重叠社团可视化。结果表明本文的算法可以弥补传统聚类布局算法的不足,细化重叠节点位置,呈现出重叠节点隶属情况,凸显了重叠社团结构;而且对比实验证实了本文布局算法符合节点均匀分布、边长一致的美学标准。

1 基本布局算法

基本网络布局算法传统上主要采用力导引布局算法,又叫FR算法[3]。力导引布局算法中节点在引力和斥力作用下进行运动,经过不断迭代,系统最终进入一种动态平衡状态,使得节点分布均匀、边长统一,符合美学原则。FR算法遵循两个原则,有边连接的节点相互靠近,但是任意节点不能离得太近。力导引布局节点之间引力和斥力的定义为

(1)

其中,fa为有边连接节点之间的引力,fr为所有节点之间的斥力,d为2个节点之间的欧式距离,k为节点之间的理想距离,理想距离k由画布的面积和节点的数量共同决定,定义为

(2)

其中,C为常数系数,S为画布的面积,N为节点个数。同时为了限制节点偏移程度,优化网络布局,算法使用了“模拟退火”原则。随着温度降低,节点的移动范围也随之变小,系统能量降低,当引力和斥力达到平衡且系统到达合适的温度时,迭代停止,算法实现收敛,达到最佳布局效果。FR算法易于理解实现,而且对称性和聚合性较好。

2 社团布局算法

社团布局算法主要对节点进行聚类布局,体现节点的局部聚合性[9]。社团布局算法先计算FR算法的引力和斥力,在此基础上计算社团中心点斥力和节点对所属社团中心节点的引力,网络节点在有边连接的节点间的引力、所有节点间的斥力、节点对所属社团的引力来更新节点位置。社团布局算法中社团中心节点之间斥力和节点对所属社团的引力定义为

(3)

其中,fca为节点对所属社团的引力,fcr为社团中心节点之间的斥力,g为引力参数,gc为斥力参数,M[v]为节点的质量,由节点度中心性进行衡量,M[Ci]为社团Ci的质量,du为社团中心节点之间的欧式距离,dv为节点与社团中心节点之间的最小欧式距离,定义为

dv=min(d1,d2,…,dk)

(4)

社团布局算法在FR算法基础上实现,符合节点均匀分布边长一致的美学原则,而且展示出社团的聚合性。算法使得不同社团节点彼此远离,相同社团节点相互靠近,显示出明显的社团结构特性以及社团内节点的相互关系。

3 重叠社团布局算法

3.1 重叠社团划分定义

复杂网络社团划分可行搜索空间如图1所示,可以分为非重叠社团划分、离散重叠社团划分和模糊重叠社团划分3类。非重叠社团划分又称为硬划分,网络中每个节点只能隶属于一个社团,且与所属社团之间具有完全的隶属关系。离散重叠划分又称为脆性重叠划分或非模糊重叠划分,网络中任意节点可以隶属于不同社团,而且对不同社团的隶属程度可以分为完全隶属和完全不隶属[13],隶属度取值为“0”或“1”,即在划分中主要考虑节点与社团的隶属关系。模糊重叠划分中网络中任意节点可以隶属于多个社团,而且重叠节点可以对不同社团有不同的隶属度,隶属度在[0,1]间取值,即在划分过程中细化了节点对社团的隶属程度。

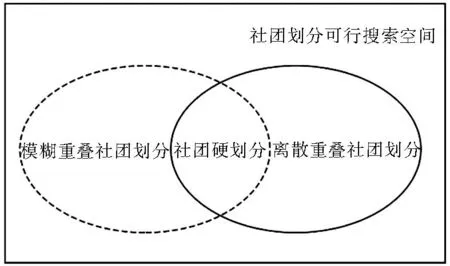
图1 社团划分可行搜索空间

目前国内外绝大多数对重叠社团的研究主要是进行社团检测优化,得到社团划分结果,而没有针对检测结果进行延伸,体现网络节点对社团细致的隶属度分布信息,从而展示重叠社团结构。传统的社团布局主要是针对非重叠社团进行布局,而没有对重叠社团可视化。本文一方面对重叠节点进行精确布局,量化重叠节点对各社团之间的隶属程度,展示重叠社团结构的精确性;另一方面,对非重叠节点进行聚类布局,体现细致、完整的社团结构信息。

3.2 问题提出和改进思路

基于FR算法实现的社团布局算法在一定程度上可以展示社团结构,但是现有社团布局算法主要针对离散社团进行可视化,而没有面向重叠社团结构进行展示。同时主流的FR算法遵循节点分布均匀、统一边长的美学原则,在重叠社团结构上的布局效果并不显著,从而影响用户对网络拓扑结构的分析。目前社团布局算法存在的问题:1)算法不能很好地应用于离散重叠社团和模糊重叠社团布局;2)算法没有针对重叠节点展现隶属度和隶属关系。本文在FR算法的基础上加入社团引力和社团斥力,实现了基于社团的力导引布局算法,同时引入节点隶属度,通过定位模型对重叠节点精确布局,利用饼图体现出多个社团的隶属程度和隶属关系。由于非重叠节点单独隶属于某个社团,而重叠节点则与多个社团间存在隶属关系,所以非重叠节点采用聚类布局的方式保证社团间布局紧密,重叠节点则采取精确定位方式确定节点位置。

3.3 重叠社团布局算法实现

3.3.1 重叠社团节点定位模型

TOA定位算法基于移动终端与基站的信号传播时间,获取终端与基站的距离,通过建立定位关系,获得用户终端位置[16]。复杂网络的重叠节点则是基于节点对社团的隶属度确定节点的准确位置,本文为了精确地对重叠节点进行展示,需要对其位置进行细致的定位,通过重叠节点与社团隶属关系与隶属程度建立定位方程,进而对重叠节点进行精确布局。

1)若网络被划分为2个社团,以社团中心节点C1,C2为圆心,k为两个社团中心的距离,kμ1,kμ2为半径画出两圆,两个距离圆相交的点则是重叠社团节点的坐标,如图2所示。由于网络节点在布局中具有一定的半径,为了满足美学原则,防止节点出现重叠,则使节点布局在交点的垂直线上。

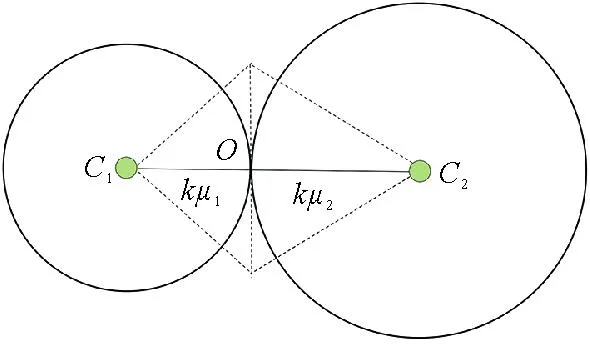
图2 2个社团的重叠节点定位

当节点隶属于2个社团时,由社团中心位置(x1,y1)和(x2,y2)可得出重叠节点位置的数学表达式为

(5)

2)若网络被划分为3个社团,以社团中心节点C1,C2,C3为圆心,k为3个社团中心距离的单位量,以kμ1,kμ2,kμ3为半径画圆,3个距离相交的点则是重叠社团节点的坐标,如图3所示。

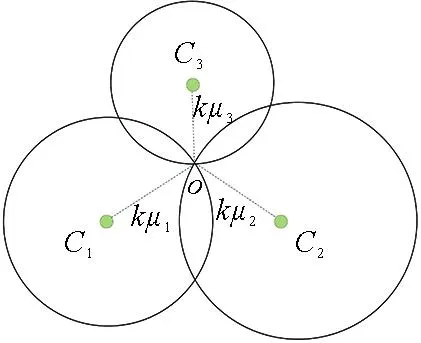
图3 3个社团的重叠节点定位

当网络节点隶属于3个社团(x1,y1)和(x2,y2),(x3,y3)时,重叠节点坐标的数学表达式为

(6)

综上所述,当网络被划分为4个社团时,以社团中心节点C1,C2,C3,C4为圆心,kμ1,kμ2,kμ3,kμ4为半径画出4个圆,4个半径相交于一点就是重叠社团节点的坐标,如图4所示。

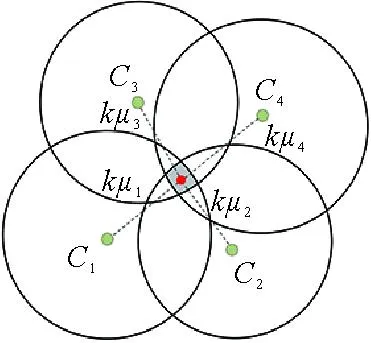
图4 4个社团的重叠节点定位

当网络节点隶属于4个社团(x1,y1),(x2,y2),(x3,y3),(x4,y4)时,重叠节点坐标的数学表达式为

(7)

如果重叠节点隶属社团大于4个,节点位置则难以进行精确定位,可以采用重叠社团算法直接进行布局,通过调整几个社团中心节点的引力和斥力作用确定节点位置。若对离散重叠社团中的重叠节点进行定位,则使得μ1=μ2=…=μm即可确定节点位置。

3.3.2 重叠社团布局算法

传统社团布局算法主要计算社团引力和斥力,通过两者作用力更新节点位置,进行网络布局。为反映重叠社团节点与社团的关系,本文布局算法使用了文献[11]的社团引力和社团斥力计算方式,在此基础上考虑了节点对社团的隶属程度和隶属关系。

设网络G为G(V,E),节点V的集合为{v1,v2,…,vn},节点对应位置为{p1,p2,…,pn},节点之间边的集合为{e1,e2,…,en},首先将重叠社团划分的隶属矩阵{μ1,μ2,…,μm}进行处理,使得节点归属于占比最大的社团,则G可被划分为k个社团{C1,C2,…,Ck},每个社团对应的社团中心为{u1,u2,…,uk},算法将社团内节点半局部中心性最高的节点作为该社团的中心节点。

为了对重叠社团节点进行进一步布局,首先将重叠社团节点归属于隶属度最高的社团,计算公式为

max(μ1,μ2,…,μm)∈Cv

(8)

其中,Cv为重叠节点所属的社团,μi为节点对社团的隶属度,计算得到重叠社团的划分结果。

为了进一步展示社团布局效果,本文为不同社团的中心节点之间添加社团斥力fcr,使得不同社团彼此远离,防止社团之间过度聚集。任意两个社团中心点斥力为

(9)

其中,‖pui-puj‖为ui和uj之间的欧氏距离,N(Ci)和N(Cj)分别为社团Ci和Cj的节点数,由于节点数目越多排斥力越大,则社团斥力与社团的规模呈正比。N为网络的总节点数,gcr为斥力参数,可以阻止不同社团节点过度靠拢,斥力参数值的选取主要取决于节点的数量和画布的大小。

为了使得社团内节点向社团中心靠拢,对社团内的节点与该社团的中心节点之间添加社团引力fcao,定义为

(10)

其中,‖pui-pk‖为节点与社团中心节点的欧式距离,gca为引力参数,通过调整该值控制社团引力的大小,与社团数目成反比,n为社团数目,μm为节点对第m个社团的隶属程度。

本文算法在社团布局算法的基础上添加了节点对社团的隶属度,因此需要先计算FR算法的引力和斥力来维持系统的平衡,随后将重叠社团节点先归属于占比较多的社团,再计算社团中心节点之间的斥力,通过节点对所属社团中心点的引力进行加权求和,节点在两者合力下更新节点位置。对节点位置迭代后,使用重叠社团节点定位模型对节点进行精确定位,使得节点隶属度与布局位置相对应。

3.3.3 重叠社团布局算法步骤

重叠社团布局算法步骤为

输入:网络G(V,E),最大迭代次数N,初始温度T,最小温度Tmin。

输出:网络节点位置坐标{p1,p2,…,pn}。

步骤1 根据输入,随机初始化节点位置,生成位置坐标{p1,p2,…,pn}。根据式8)计算节点所属社团,得到社团划分结果C。

步骤2 根据式1)和式2)计算所有节点之间的斥力和有边相连节点之间的引力,更新节点位置。

步骤3 根据式9)计算所有社团中心节点之间的斥力值,更新节点位置。

步骤4 根据式10)计算所有社团内节点对社团的中心节点的引力值,更新节点位置。

步骤5 若系统的温度小于最小温度或者迭代次数大于最大迭代次数N,执行下一步,否则转步骤2。

步骤6 根据重叠节点定位模型对社团重叠节点进行精确定位,输出所有节点的位置,算法结束。

在重叠网络社团布局算法中,通过FR的模拟退火算法进行收敛,初始温度随着迭代次数的增加而不断下降,当系统温度趋近于0时表示网络布局达到最终的稳定状态。步骤1为所有节点随机生成位置,步骤2至步骤5为循环,通过计算节点的斥力、引力以及社团中心点的社团斥力、节点对社团中心点的社团引力,进而更新节点的位置,直至系统温度小于给定的下限阈值或者迭代次数超过N;否则,继续调整节点位置。最后,通过重叠节点定位模型对节点进行精确定位,更新重叠节点位置。

4 实验结果分析

为了验证重叠社团布局算法的可视化效果,本文选取了FR算法和文献[8]等布局结果进行对比,FR算法、文献[8]和文献[11]算法是先划分社团再可视化布局,CGDA算法[9]是边聚类边布局方式,可以从两个方面与本文算法形成明显对比。由于本文算法采用的社团划分算法为模糊重叠社团发现算法,不同于对比算法硬划分的方式,因此社团划分的结果与之不同,但最终可视化结果主要针对网络社团结构进行有效展示。网络拥挤程度可以刻画节点分布的均匀性,边长偏差可以体现边长的匀称性,为定量分析本文算法的合理性,选取点分布方差、边长偏差、节点分布偏差实验指标进行实验,为真实反映实验结果,算法对比数据源于文献[17]。

4.1 重叠社团可视化结果分析

Dolphins网络数据集描述的是生活在新西兰的62只海豚形成的社会关系网络,节点代表海豚,边代表海豚之间的接触次数,网络包含62个节点和152条边。本文算法与文献[8]算法、CGDA算法[9]在Dolphins网络数据集的布局结果如图5所示。文献[8]算法只能针对非重叠社团进行布局,而且该算法虽然阻止了不同社团节点位置错杂现象,但是网络节点过于拥挤,若无颜色区分,用户很难发现社团结构。CGDA算法相较于朱志良算法清晰地展示了社团结构,但是难以对重叠社团进行展示。本文通过饼图形式精确表示出社团隶属度,直观展示出重叠网络节点以及重叠程度,用不同的颜色标识社团信息,在布局上隶属于某个社团的隶属程度越大则距离该社团更近。从图5c可视化结果中可以看出,节点8,19,20,37,39等节点为网络中的共享节点,这些节点位于社团边界位置,展示了对几个社团的贡献程度和归属关系。本文的重叠社团布局算法能够很好地应用于重叠社团,清晰地展示了重叠社团节点且社团结构较为显著,整个网络图具有很强的对称性。

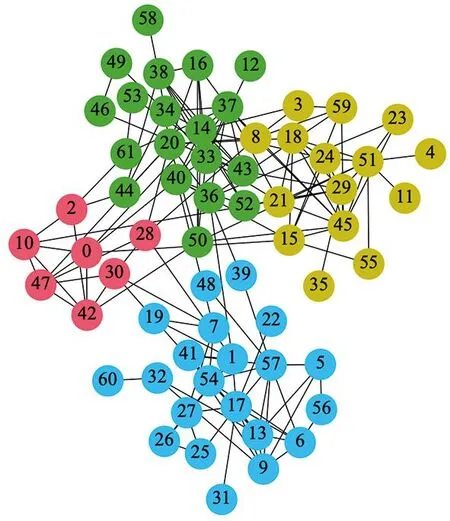
a 文献[8]布局结果

Football网络数据集描述的是美国足球联赛构成的社交网络,节点代表足球队,边代表两只球队进行过一次比赛,网络包含115个节点和616条边。与Dolphins网络相比,数据集较为庞大,需要对网络节点进行缩小来展示。从图6可以看出FR算法无法满足复杂的网络展示的美学需求,难以对社团结构进行展示。文献[11]的算法虽然对网络层次结构进行了明显的区分,但是它只针对非重叠社团结构进行可视化,本文布局算法既展示了网络的层次结构,又对重叠节点的隶属程度和隶属关系进行了很好的呈现。

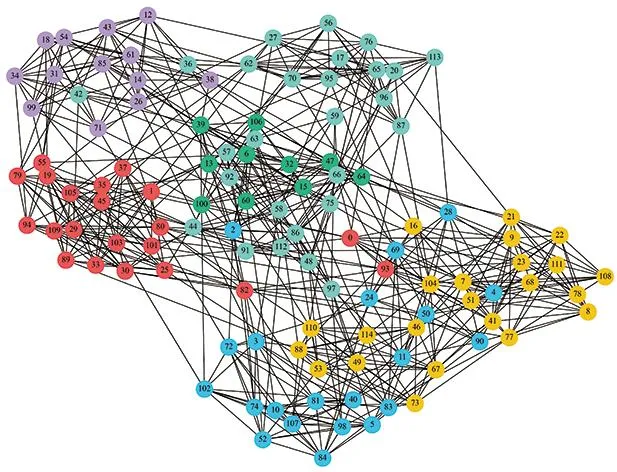
a FR算法布局结果

4.2 实验指标分析

为了验证布局效果的有效性,通过美学标准以及布局结果带给人的直观感受分析布局效果。Sugiyama、Sindre和Purchase等在几年的时间里提出了16项网络绘图的美学标准,其中5项美学标准是普遍适用的,包括最少的边交叉数量、相邻节点位置相接近、直线边、节点密度均匀及对称性[18]。对于网络社团结构可视化而言,希望最终的布局效果尽可能满足上述指标。本文主要通过文献[8]、文献[19]提出的点分布方差、边长偏差、节点偏差对相同数据集进行对比分析。

4.2.1 点分布方差

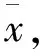
(11)

4.2.2 边长偏差

边长的均匀程度体现了布局算法的美学原则,因此将最小边长和最大边长和平均边长的差值作为衡量标准,将边长记为l,将边长偏差记side_length_deviation。公式定义为

(12)

4.2.3 节点分布偏差

节点的最小距离展现了布局算法中斥力的作用效果,将最佳分布距离减去最小节点距离的绝对值与图的显示面积的比值作为节点分布偏差,记为node_distribution_deviation。公式定义为

(13)

其中,最佳距离为图的显示面积与图节点数量的比值,定义为

(14)

由表1和表2以及可视化结果分析可知,选取相同网络数据集进行实验,本文算法相较于其他算法点分布方差较小,说明算法布局可以有效减少节点错杂以及降低局部拓扑结构的混乱现象。同时本文算法节点分布方差较低,表明节点分布更为均匀,符合网络布局的美学标准,而且可以降低布局的拥挤程度。由于重叠社团布局算法将重叠节点分布在几个社团之间,相较于其他布局算法节点分布偏差较小,对重叠节点进行精确布局可能会使得边长出现少量拉伸现象,但重叠节点相较于整个网络节点较少,尚在用户可接受范围。

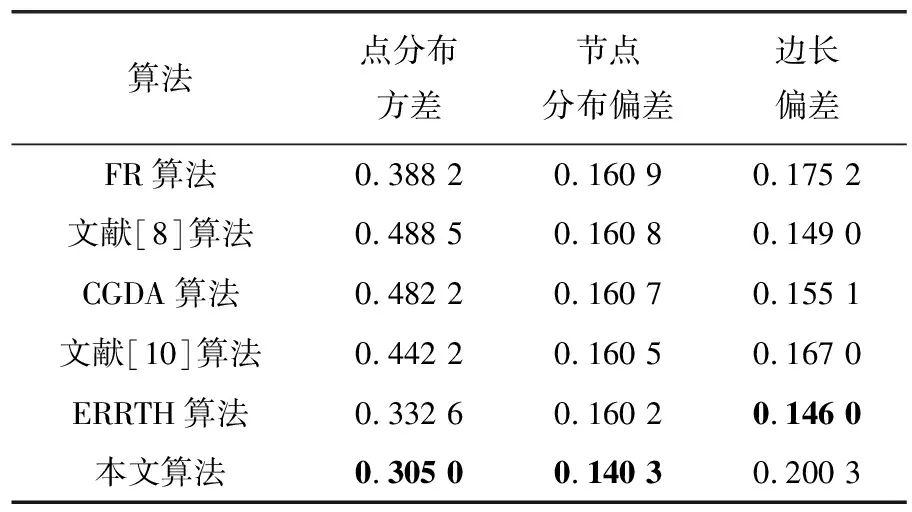
表1 Dolphins网络的实验结果

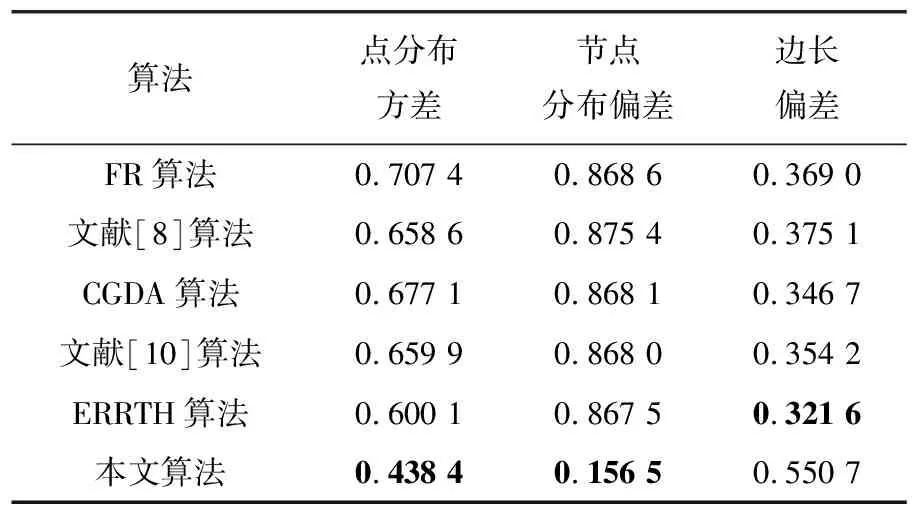
表2 Football网络的实验结果

5 结论

针对复杂网络重叠社团结构的可视化需求,本文在传统的社团结构布局算法基础上融入了社团隶属度,在布局上对重叠节点进行精确布局,在视觉展示上通过饼图对重叠节点进行编码,选取不同颜色对节点隶属程度进行着色。实验结果表明本文算法节点分布均匀,而且降低了节点密集程度,满足了美学标准,在位置布局以及视觉上对重叠节点的展示提高了重叠节点的辨识度,体现出重叠社团的网络特征。与传统社团布局算法相比,本文算法可以直观呈现出重叠社团节点的隶属程度以及隶属关系,同时保留了网络的聚类布局效果,弥补了传统社团布局算法不能对重叠社团结构展示的缺陷,丰富了网络布局。

本文主要针对全局社团结构进行可视化,而没有考虑局部社团结构,区域内的节点聚类是分析网络社团的重要方式。因此,在下一步工作中,可以采用相应布局算法对局部社团结构进行布局,体现出局部拓扑结构信息。本文算法可以对重叠社团进行很好的呈现,但是由于需要对重叠节点进行二次布局,使得该布局算法时间略高于其它布局算法,今后可以结合网络拓扑结构,在社团划分的同时进行布局,加快算法布局速度。