中国铁路快捷货物运输网络复杂性分析

马 亮,金福才,胡宸瀚

(1.西南交通大学信息科学与技术学院,成都 611756;2.国家铁路智能运输系统工程技术研究中心,北京 100844;3.中国铁道科学研究院集团有限公司电子计算技术研究所,北京 100081)

0 引言

地震、风灾、滑坡等自然灾害的发生和线路、信号、供电等关键设备的故障可能会降低铁路运输效率和通过能力[1],甚至会发生大面积车流挤压、列车晚点和运行取消等情况[2]。为降低铁路事故的发生频率和严重度,需要对铁路网络进行建模,并分析铁路网络的静态拓扑特性和动态传播特性,为铁路的日常维护和应急管理提供支持。铁路网络是规模庞大、复杂度高、受外界影响大的巨型动态复杂网络系统[3]。基于复杂网络建模和分析方法,可以从不同的逻辑角度分析铁路网络的静态拓扑特征和动态演化机理,为解决铁路网络发展规划、运营保障和运输组织优化等问题提供理论依据。随着高铁快运、跨境联运等多种新型快运业务的不断增长,对铁路快捷货物运输网络进行复杂性分析有助于提高铁路运营维护和应急管理水平,是铁路运输领域的关键科学问题。

针对铁路复杂网络建模和拓扑结构研究:胡宸瀚等[4]归纳了P,R,L等3种空间下的铁路网络建模方法和特性分析方法;冯佳等[5]在L空间构建了城市轨道交通流网络模型,分析了小世界特性与交通流特性;WANG Li等[6]建立了铁路物理网络和铁路车流网络,基于网络效率贡献度指标对网络中的关键站点进行了定量分析;王小荣[7]和詹斌等[8]分别构建了铁路快速货运物理网络和L空间的无权网络,分析了网络的小世界、无标度和节点中心等拓扑特性。针对铁路网络鲁棒性、脆弱性或者抗毁性分析研究:Yin等[9]提出了地震灾害高发区的地理铁路网的鲁棒性评估方法;Gu等[10]提出了基于聚集社团指标的高速铁路网络鲁棒性评价方法;于宝等[11]通过计算网络效率和最大连通子图得到高速铁路网络在随机攻击下和蓄意攻击下均比较脆弱;刘朝阳等[12]仿真计算了城市轨道交通网络在不同失效策略下的级联失效抗毁性。上述研究取得了较好的成果,然而已有的复杂网络模型中较少考虑货运车流量对车站间连接紧密程度的刻画,导致模型和分析的结论脱离实际。现有无权网络复杂性分析方法已经不适用于加权网络,单一的重要度评价指标与鲁棒性分析方法无法全面分析网络的复杂性,需要继续完善拓扑性能指标、节点的重要度评价指标和鲁棒性分析方法。

本文选取中国铁路快捷货运系统网络(Chinese Railway Express Freight Transportation Network,CREFTN)为研究对象,提出L空间下中国铁路快捷货运系统的无向加权复杂网络模型(Undirected and Weighted Complex Network Model of CREFTN,UWCN-CREFTN)构建方法、节点重要度综合评价方法和基于综合重要度节点失效的网络鲁棒性分析方法。依据实际的中国铁路快捷货运时刻表和车站间日均交互车流量数据,客观全面地定量分析网络的静态拓扑特性和节点重要性;基于加权网络效率指标,定量对比分析节点随机失效和蓄意破坏2个方面4种情形下网络的鲁棒性;最后,给出对网络鲁棒性影响较大的关键车站列表。

1 中国铁路快捷货运加权复杂网络建模

铁路物理网络由车站和线路构成,铁路快捷货运系统是在铁路物理网络的基础上,通过快捷货运组织技术实现零散货物、批量散货、行包、高铁、联运等多种制式的快捷运输,是铁路物理网络和快捷货运列车之间耦合产生的逻辑网络,包括P空间、R空间和L空间等3种逻辑复杂网络模型[1]。为研究CREFTN结构对货物快捷运输效率的影响,在铁路快捷货运列车成对开行和车站间交互车流均衡的前提下,在L空间建立CREFTN的加权复杂网络模型。

令铁路物理网络为G=(P,E),其中P={p1,p2,…,pN}为铁路货运车站集合,N为车站数量,E={eij|i,j=1,2,…,N}为边集合,若车站pi和pj之间存在线路,则eij=1,否则eij=0。令铁路快捷货运列车集合为T={t1,t2,…,tM},M为列车数量,任意列车tk=(Pk,Ck),Pk∈P为列车tk停靠并办理货车中转的车站集合,Ck为列车tk在车站办理货运中转车辆数集合。通过铁路物理网络与铁路快捷货运列车耦合得到L空间UWCN-CREFTN模型记为三元组[1-2]:GW=(P,L,W)=G⊕T,耦合关系“⊕”表示:若G中的两个车站至少是同一趟快捷货运列车连续停靠且办理货运中转业务的车站,则这两个车站之间存在一条边。L={lij|i,j=1,2,…,N}为表征节点间耦合连接关系的邻接矩阵,若车站pi和pj之间存在边,则lij=1,否则lij=0。W={wij|i,j=1,2,…,N}为边的权值集合,元素wij为车站之间日均交互车辆数。若任意两个节点wij=lij时,则为无权网络。如图1所示为UWCN-CREFTN模型建立过程示意图,模型中线条宽度与车站间交互的货运量成正比。由于p1和p4,p3和p4,p4和p6等节点对之间不存在车流耦合关系,因此在模型中这些节点之间的边被约减。由于至少有2趟列车连续停靠车站p2和p4,p5和p7,因此模型中车站p2和p4,p5和p7间的连线较宽。

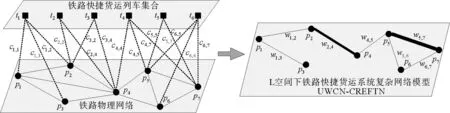
图1 铁路物理网络与铁路快捷货运列车耦合示意图

通过上述建模方法,以“中国铁路95306网站”上公开的161列快运货物班列和362列直达货物班列时刻表,以及车站间日均交互车流量数据为基础,在L空间建立的UWCN-CREFTN模型如图2所示,网络包含了350个节点和468条边,图中红色点表示承担快捷货运中转业务的车站,蓝色连线表示相邻车站之间有快捷货运列车停留并有车流中转业务,连线的宽度与边的权值成正比。由图2可见铁路承担快捷货运的车站较多分布在中国环渤海、长江中游、长三角、成渝、珠三角和中原等城市群或者经济群,与这些区域的经济活跃和铁路货运需求程度相关。

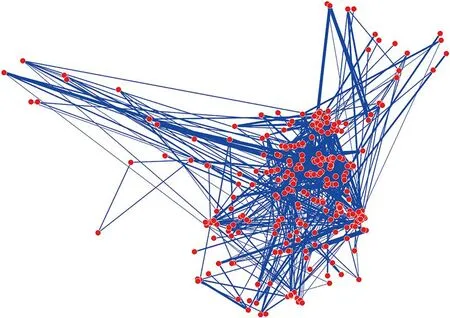
图2 在L空间下UWCN-CREFTN模型结构图

2 铁路快捷货运网络复杂性分析方法

2.1 加权复杂网络性能指标

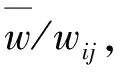
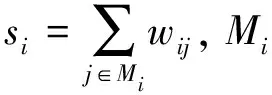
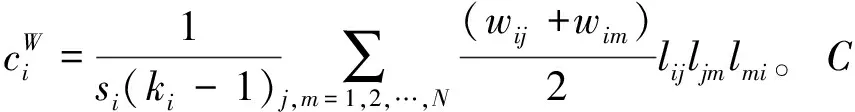
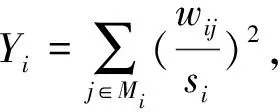
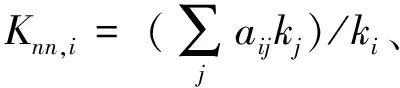
2.2 加权复杂网络综合重要度指标

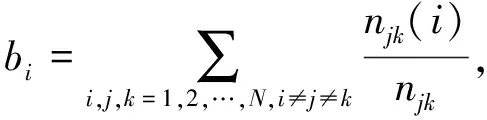
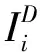
2.3 基于效率的加权复杂网络鲁棒性分析方法

1)节点失效或者遭受蓄意破坏是指车站丧失货运车流中转能力,保留列车接发和通过能力。节点失效之后只影响模型中相邻节点间的车流交互,并不影响其他节点间的车流交互。若在节点被移除之后出现部分剩余节点之间路径不连通时,那么不连通节点之间的效率记为0。

2)节点随机失效下网络的鲁棒性:随机从网络中移除节点,并移除与该节点相连的所有边,计算Ri,直至网络中所有的节点被移除或者效率累积下降率达到100%。为降低随机性,重复多次上述过程,计算节点失效率对应Ri的平均值。

3)从最大加权介数、最大强度和最大综合重要度三种情况分析节点受到蓄意破坏时网络的鲁棒性:对网络中节点按照加权介数(强度、综合重要度)从大到小进行排序,依次移除网络中加权介数(强度、综合重要度)最大的节点,并移除与该节点相连的所有边,重新计算网络的效率Ri,直至网络中所有的节点被移除或者效率下降率达到100%。

3 铁路快捷货运网络复杂性分析

3.1 加权复杂网络模型的拓扑特性分析

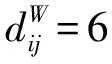
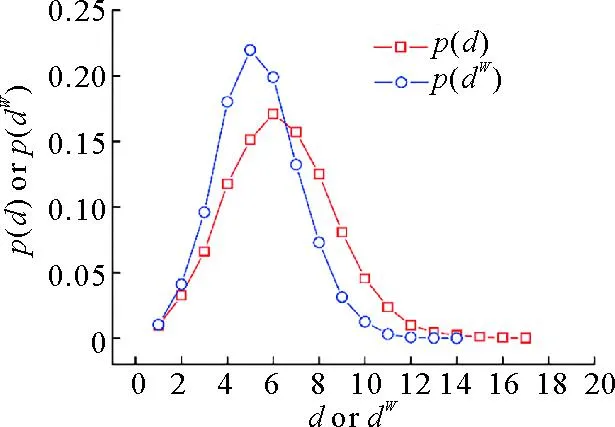
图3 无权网络和加权网络距离概率分布曲线

通过计算得到:网络中所有点的平均强度为105.906,表明每日平均有105.906辆货车到达这些车站,图4所示为UWCN-CREFTN的强度分布曲线图,图5所示为强度区间内车站数分布柱状图,从图4和图5可以看出只有少部分车站的强度较大,绝大部分车站的强度小于350。

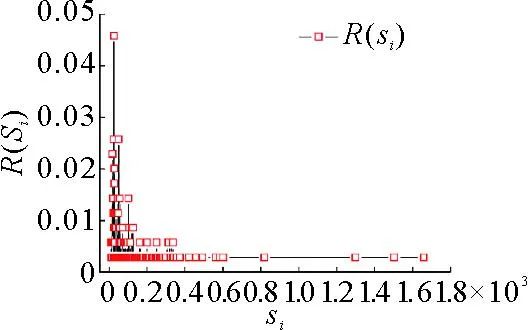
图4 点强度分布曲线图

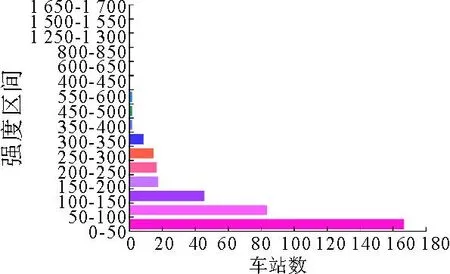
图5 强度区间内车站数分布柱状图

图6所示为节点累积强度分布曲线,经拟合得到具有典型的幂率分布R(s≥si)∝e-0.015 7si,表明:UWCN-CREFTN具有高度的异质性,只有少数车站在货物快捷运输中起到了关键作用,这些车站具有较强的车流处理能力。通过计算得到节点的平均强度与度之间的关系曲线如图7所示,经曲线拟合得到节点的平均强度与节点度之间存在幂律关系:〈si〉∝ki2.372 7,表明:度数越大的节点强度越大,强度的增长快于度的增长,即车站服务能力的增长快于连通度的增长。由此可以说明:在当前铁路网络基础设施条件下,可以通过提高幂指数的取值来提高铁路快捷货运的服务能力,但是物理网络中区间通过能力和车站作业能力的限制使得幂指数的增大受限,需要通过运输组织策略调整和路网结构优化共同来提高运输效率,譬如:调整装车流、优化列车编组计划、优化运行径路、提高瓶颈区段和车站的能力等,实现车流动态分布与路网运输能力的最优匹配。

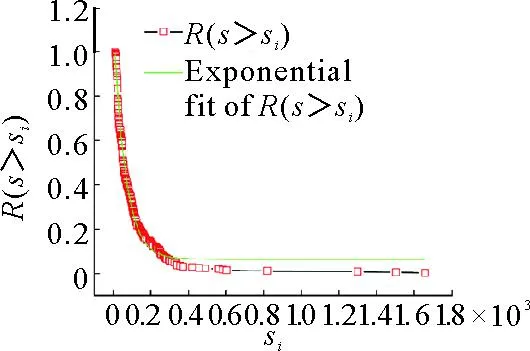
图6 节点累积强度分布曲线

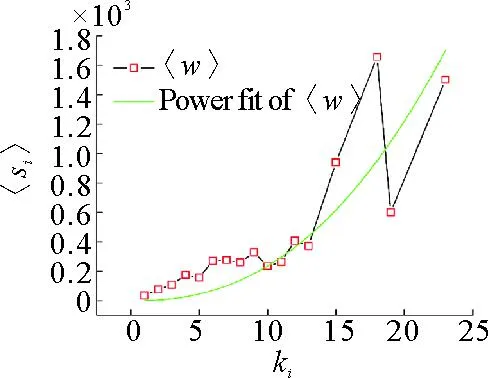
图7 点度数与平均强度关系曲线

通过计算得到:无权网络平均聚集系数C为0.035 3,加权网络聚集系数CW为0.034 7,尽管远小于规则网络聚集系数0.5,但是比随机网络聚集系数0.002 85要大得多,介于规则和随机之间,表明UWCN-CREFTN具有小世界特征[1],即网络中任意两个节点间都可以找到一条相对较短的路径,且节点之间存在较强的聚集性。从图8中聚集系数与度数关系的曲线可得:绝大多数C(k)>CW(k),也就是网络的拓扑聚集取决于权低的边,意味着具有较强车流处理能力的车站偏好与相关车站之间有更多的车流交互,这可以解释为:比较重要的车站形成稳定的集团就能处理更多的车流。

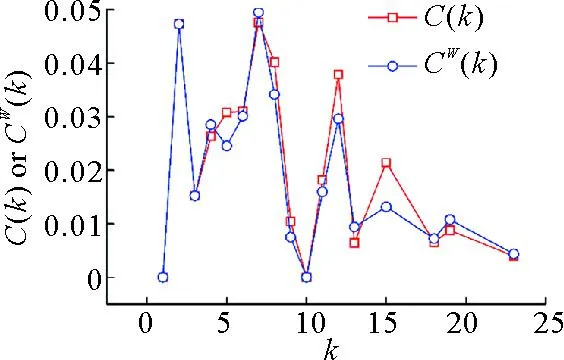
图8 网络平均聚集系数与度数关系曲线

通过计算得到均等性Yi与点度数ki之间关系曲线如图9所示,经曲线拟合得到存在幂律关系:Yi∝ki-0.864 37,接近于ki-1。说明:随着度数的增大,点的不等性下降较快,边的权值对节点的强度贡献度比较均衡,即车站与其相邻车站之间交互车流数比较均衡。

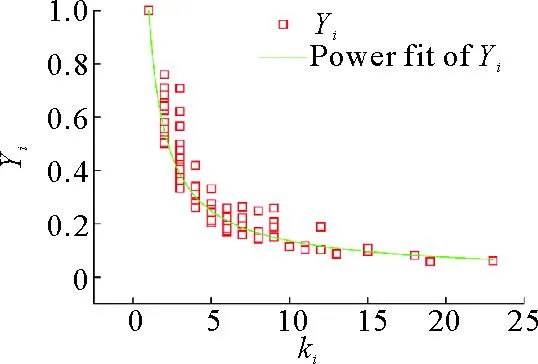
图9 点度数与点权不等性关系曲线

通过计算得到最近邻点平均度与最近邻点加权平均度的关系曲线如图10所示,从图10可以得到:绝大多数强度较大的节点偏好与度数较小的节点相连,节点之间相互作用属于加权非同类匹配性,即绝大多数节点偏好于与度数较小节点连接。通过计算得到节点强度与邻接节点平均强度之间的关系曲线如图11所示,从图11可以得到:不同距离的邻接节点平均强度与节点强度分布趋势比较一致,节点间存在强度-强度负相关性,强度较小的节点偏好与强度较大的邻接节点相连,强度较大的节点偏好与强度较小的邻接节点相连。

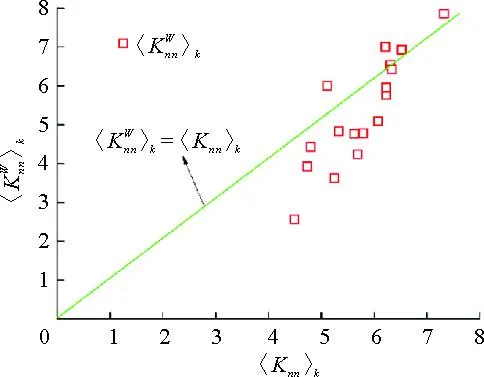
图10 节点间同类匹配关系曲线

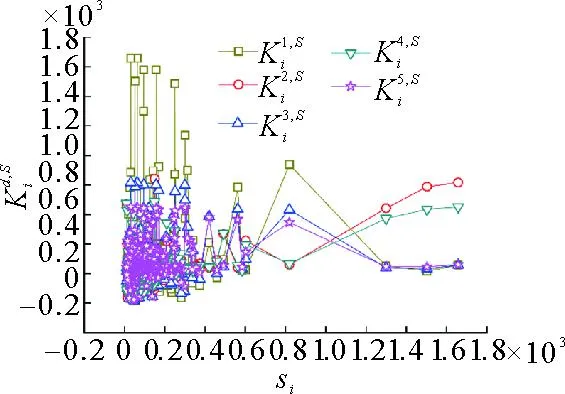
图11 节点强度与邻接节点平均强度之间关系曲线

3.2 加权复杂网络模型的节点重要性分析

表1 综合重要度较大的20个车站表

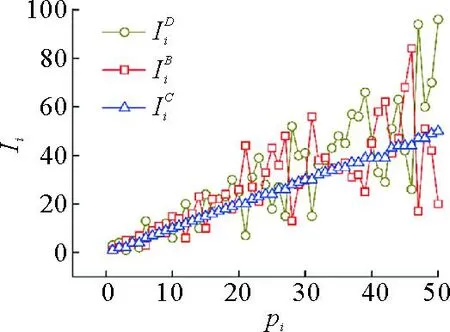
图12 前50个车站对应重要度对比分析曲线图

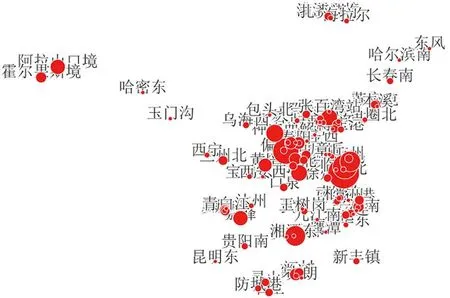
图13 综合总要度较大的前100个车站的分布图

从强度、加权介数和综合重要度3个指标对比分析得到:1)比较重要的车站基本上是大型的技术站和边境口岸站,且集中分布在中国中东部地区,这与相关区域的经济活跃程度和货运需求旺盛正相关,而部分出入境口岸站的重要性大与办理大量的国际联运业务相关。2)绝大多数车站的重要度比较小,少数比较重要的车站成为“中心节点”,部分比较重要的车站之间相互吸引形成集团,这些高等级车站的集中设置,为客户办理货运业务提供了更多的选择。

3.3 加权复杂网络模型的鲁棒性对比分析

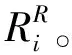
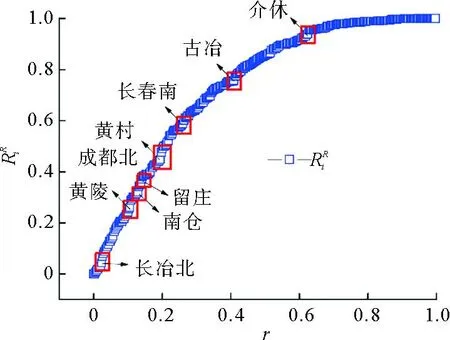
图14 基于随机失效的网络鲁棒性变化曲线

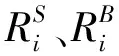
图15 三种蓄意破坏下网络鲁棒性变化曲线

从图15对比分析得到:网络效率下降率与3种破坏的车站比例近似呈指数分布;最大加权介数和最大综合重要度破坏的车站比例为7%,最大强度破坏的车站比例为9.5%时,网络效率下降达到90%;最大强度和最大综合重要度破坏的车站比例达到38%,最大加权介数破坏的车站比例达到99.4%时,网络接近完全崩溃。因此,最大加权介数破坏和最大综合重要度破坏比最大强度破坏使网络变得更脆弱,最大加权介数破坏比最大综合重要度破坏更甚,最大强度破坏和最大综合重要度破坏比最大加权介数破坏更快地造成网络崩溃。

排序前20的车站依次受到最大强度、最大加权介数和最大综合重要度破坏之后,网络的累积效率下降了69.4%,85.1%和85.0%。表2为综合重要度最大的车站依次受破坏后网络效率累积下降率表,这些车站需要重点保护,一旦遭受破坏或者故障会对快捷货运网络的运输效率产生较大的影响。

表2 对网络鲁棒性影响较大的关键车站

4 结论

本文提出了中国铁路快捷货运无向加权复杂网络建模方法、节点重要度综合评价方法和基于节点失效的网络鲁棒性分析方法。通过实例验证表明:与无权网络建模与分析方法相比,本文方法能够更全面、客观和准确地分析铁路快捷货运系统网络的复杂性。在本文研究的基础上,以提高网络的鲁棒性、连通性和效率为目标,通过对比分析新建改造铁路基础设施和调整铁路货运组织方案等措施对网络性能的影响,进而为中国铁路货运系统网络规划和组织优化提供决策支持。