例析函数零点问题的类型及应对策略

广东省佛山市南海区金石实验中学(528225) 徐正印

近年高考试题常常出现确定或证明含有参数的函数零点(交点)的个数或根据含有参数的函数零点的个数求参数取值范围的问题.这类问题通常融合了数形结合、分离参数、等价转化等数学思想方法,能较好地反映学生分析问题(观察能力)和解决问题的能力,突出选拔性,备受命题者的青睐,常常困扰考生无法选择恰当的方法.这类题目一般有两问,我们只须根据题目第一问的设问特点,就能及时选择恰当的解题方法.

标志一题目没有涉及讨论函数的单调性,参数容易分离,且分离后得到的函数的导数容易求出.

应对策略分离参数法,即分离参数,将原函数零点的问题转化为一个函数(该函数求导不复杂)与一条与y轴垂直的直线交点的问题.

例1(2015 年高考新课标Ⅰ卷文科) 函数f(x) =e2x-alnx.

(1)讨论f(x)的导函数f′(x)的零点的个数;(2)略.

解(1) 易知,f′(x) 的零点的个数⇔y= 2xe2x(x>0) 的图象与y=a的图象交点的个数.

设g(x) = 2xe2x(x>0), 则g′(x)=2(1+2x)e2x,在(0,+∞)上,g′(x) > 0,g(x) 单调递增.当x→ 0+时,g(x) → 0+; 当x→+∞时,g(x) →+∞; 函数y= 2xe2x(x>0) 的大致图象如图1 所示.

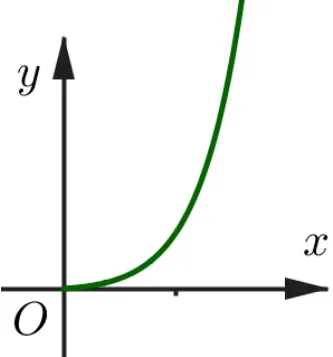
图1

当a≤0 时,y=2xe2x(x>0)图象与直线y=a没有交点,f′(x)的零点的个数为0;当a> 0 时,y= 2xe2x(x> 0)图象与直线y=a的图象有且只有一个交点,f′(x)的零点的个数为1.故,当a≤0 时,f′(x)零点个数为0;当a> 0时,f′(x)零点个数为1.

例2(2018 年高考新课标Ⅱ卷理科第21 题)已知函数f(x)=ex-ax2.

(1)略;(2)若f(x)在(0,+∞)上只有一个零点,求a.

解(2) 当x> 0 时,.f(x) 在(0,+∞) 上只有一个零点只有一个正根的图象与y=a的图象只有一个交点.设, 则, 在(0,2) 上,g′(x) < 0,g(x)单调递减; 在(2,+∞)上,g′(x) > 0,g(x)单调递增;.当x→0+时,g(x) →+∞.因为与y=a只有一个交点,所以.

类似题1.1 (2016 年高考新课标Ⅰ卷理科) 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围;(2)略.

类似题1.2(2022 年高考全国乙卷理科第21 题)已知函数f(x)=ln(1+x)+axe-x.

(1)略;(2)若f(x)在区间(-1,0)、(0,+∞)各恰有一个零点,求a的取值范围.

标志二题目第一问只讨论参数取某一值时函数的单调性,没有讨论参数取其它值时函数的单调性.参数容易分离,且分离后得到的函数的导数容易求出.

应对策略分离参数法,即分离参数,将原函数零点的问题转化为一个函数(该函数求导不复杂)与一条与y轴垂直的直线交点的问题.

例3(2020 年高考新课标Ⅰ卷文科第20 题) 已知函数f(x)=ex-a(x+2).

(1)当a=1 时,讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围.

解(1)略.(2)易知f(-2)=e-20,-2 不是f(x)的零点.当x-2 时,.f(x)有两个零点的图象与y=a的图象有两个交点.设, 则, 在(-∞,-2)、(-2,-1) 上,g′(x) < 0,g(x) 单调递减.在(-1,+∞) 上,g′(x) > 0,g(x) 单调递增.在(-1,+∞) 上,g′(x) > 0..在(-∞,-2) 上,g(x) < 0; 当x→-∞时,g(x) →0; 当x→-2-时,g(x)→-∞;当x→-2+时,g(x)→+∞;当x→+∞时,g(x)→+∞.

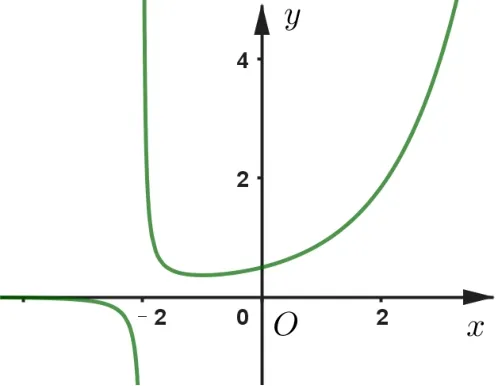
图2

类似题2.1(2018 年高考新课标Ⅱ卷文科第21 题)已知函数f(x)=-a(x2+x+1).

(1)当a=3 时,求f(x)的单调区间;

(2)证明:f(x)只有一个零点.

标志三题目第一问明确讨论函数的单调性.

应对策略利用函数的单调性和零点存在定理.

例4(2019 高考新课标Ⅱ卷理科第20 题)已知.

(1)求f(x)的单调性,并证明f(x)有且仅有两个零点;(2)略.

解(1), 在(0,1)、(1,+∞)上,f′(x)>0,f(x)单调递增.因为

所以f(x)在(1,+∞)上有唯一零点.因为

所以f(x)在(0,1)上有唯一的根.

综上所述,f(x)有且仅有两个零点.

类似题3.1 (2015 年高考北京卷文科第19 题) 设函数,k>0.

(1)求f(x)的单调区间和极值;

(2)求证: 若f(x)存在零点,则f(x)在区间上仅有一个零点.

类似题3.2(2020 年高考新课标Ⅲ卷文科第20 题)已知函数f(x)=x3-kx+k2.

(1)讨论f(x)的单调性;

(2)若f(x)有三个零点,求k的取值范围.

类似题3.3(2021 年高考甲卷文科第20 题) 设函数f(x)=a2x2+ax-3 lnx+1,其中a>0.

(1)讨论f(x)的单调性;

(2)若y=f(x)的图像与x轴没有公共点,求a的取值范围.

类似题3.4(2017 年高考新课标Ⅰ卷理科第21 题)已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围.

类似题3.5(2016 年高考新课标Ⅰ卷文科第21 题)已知函数f(x)=(x-2)ex+a(x-1)2.

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围.

标志四题目中没有要求讨论函数的单调性,参数也不能分离参数或分离参数得到的函数求导复杂.

应对策略解决问题的方法要利用函数的单调性.

例5(2022 年高考全国乙卷文科第20 题) 已知函数.

(1)当a=0 时,求f(x)的最大值;

(2)若f(x)恰有一个零点,求a的取值范围.

解(1)略;(2)

1)当a≤0 时,在(0,1)上,f′(x) > 0,f(x)单调递增;在(1,+∞)时,f′(x)<0,f(x)单调递减;fmax(x)=f(1)=a-1<0,此时函数无零点,不合题意.

2)当a>0 时,

(ⅰ)当0 0,f(x) 单调递增; 在上,f′(x) < 0,f(x) 单调递减.f(1)=a-1<0,当x→+∞时,f(x)→+∞;f(x)仅在有唯一零点,符合题意.

(ⅱ) 当a= 1 时,, 在(0,+∞) 上,f′(x) ≥0,f(x) 单调递增;f(1) =a- 1 = 0,f(x) 有唯一零点,符合题意.

(ⅲ) 当a> 1 时, 在、(1,+∞) 上,f′(x) > 0,f(x) 单调递增; 在上,f′(x) < 0,f(x) 单调递减;f(1) =a-1 > 0,,当n→+∞,;f(x) 在有一个零点, 在无零点,f(x)有唯一零点,符合题意.

综上所述,a的取值范围为(0,+∞).

类似题4.1(2019 年高考新课标Ⅰ卷文科第20 题)已知函数f(x)=2 sinx-xcosx-x,f′(x)为f(x)的导数.

(1)f′(x)在区间(0,π)存在唯一零点;

(2)当x∈[0,π],f(x)≥ax,求a的取值范围.

类似题4.2(2019 年高考新课标ⅠⅠ卷理科第20 题)已知函数f(x)=sinx-ln(x+1),f′(x)为f(x)的导数,求证:

(1)f′(x)在区间存在唯一极大值点;

(2)f(x)有且仅有2 个零点.

类似题4.3(2020 年高考新课标Ⅲ理科第21 题节选)设,若f(x)有一个绝对值不大于1 的零点,证明:f(x)所有零点的绝对值都不大于1.