圆盘弯曲振动固有特性研究

李 亮，王 展，刘富豪，卢小雨

(安徽理工大学 a 力学与光电物理学院；b 机械工程学院，安徽 淮南 232001)

圆盘结构在工程上有广泛的应用，圆盘刀[1]、圆盘剪切机[2]、圆盘换能器[3]、圆盘施肥器[4]等都是其应用实例。研究圆盘弯曲振动特性对于预防结构共振、提高结构强度和使用寿命、设计结构振动控制方案等都具有重要的意义。已有涉及圆盘振动的研究：任红军等[5]使用理论分析、实验测试和有限元仿真3 种方法求解了中心固支旋转薄壁圆盘线性行波特性；邱金波等[6-9]探讨了圆盘振动的主动控制问题，提出了模态空间控制法、自传感电磁控制法、非接触式电磁作动器等控制方案，并对圆盘振动控制问题进行了综述；袁艳玲等[10]研究了圆盘振动特性的理论求解方法，采用多种简化计算方法求解圆盘弯曲振动频率，与实验结果进行对比，探讨了振动参数的设计问题；朱林等[11]对圆盘弯曲振动特性进行了实验测试；冯中营等[12]使用ANSYS 分析了打孔圆盘的振动频率。

由于圆盘弯曲振动的理论精确解难以求解，单独的有限元数值模拟或单独的实验测试又易产生无效的结果，难以确定弯曲振动频率，本研究使用有限元与实验相结合的方法求解圆盘弯曲振动频率和模态。考虑中心固支圆盘弯曲振动约束模态，首先使用有限元方法对弯曲振动频率进行预估计，然后组织实验测试，并根据预估的有限元结果确定实验频率，最后用实验结果对有限元结果进行验证。该方法可应用于实验测试，也可应用于拓展性实验教学。实验设备采用安徽理工大学工程力学系智能结构与振动控制实验室的XL3419 型多功能振动实验教学设备，实验模型采用教学用圆盘模型。计算软件选用ANSYS R17.0数值仿真商业软件。

1 圆盘弯曲振动的有限元分析

实验测试之前，首先进行有限元数值仿真，对圆盘弯曲频率进行估算。分析采用ANSYS R17.0 商业软件。以下各小节给出有限元分析的步骤和计算结果。

1.1 有限元模型

按照实验测试模型的几何参数建立圆盘的三维几何模型，其中圆盘直径为240 mm，中间圆孔直径为10 mm，厚度为3 mm。图1 为所建几何模型的示意图。

图1 圆盘的三维几何模型

1.2 材料参数设置

根据实验模型的材料属性设置圆盘物理参数。圆盘材料为均匀各向同性材料，其密度为7 850kg/m3，弹性模量为200GPa，泊松比为0.3，体积模量166.67 GPa，剪切模量76.9 GPa。

1.3 网格划分

在ANSYS workbench 软件中，对圆盘进行网格划分。圆盘结构非常规则，采用自动划分网格的形式对其进行网格划分，划分结果如图2 所示，节点总数为6 180，单元总数为850。

图2 网格划分结果

1.4 模态分析

考虑圆盘中心固支约束，在Model 模块对圆盘设置Fixed support，对其内圈孔面进行固定。设置好约束后，对圆盘振动模态进行求解，得到有限元计算结果，然后进行后处理工作。对计算所得的整体变形（Total Deformation）图，逐个进行观察，挑选弯曲振动振型和频率。弯曲振动为Z 方向的变形，通过挑选Z 方向的变形，得到圆盘弯曲振动振型。由于动能主要集中在低阶模态，本研究只考虑前三阶弯曲模态。图3 给出了圆盘弯曲振动前三阶振型的有限元结果，图像显示：第一阶弯曲振型只在圆盘中心位置处存在1 个节点，圆盘各点在节点的同一侧振动；第二阶和第三阶弯曲振型分别出现1 个和2 个节圆（图中蓝色圆线），节圆两侧的点分别沿不同方向振动。本文所得圆盘弯曲振动前三阶振型与文献[10-12]所得结果一致。前三阶弯曲振型所对应的频率即为前三阶弯曲频率，其值分别为196.7 Hz、1 124.3 Hz 和3 267.7 Hz。

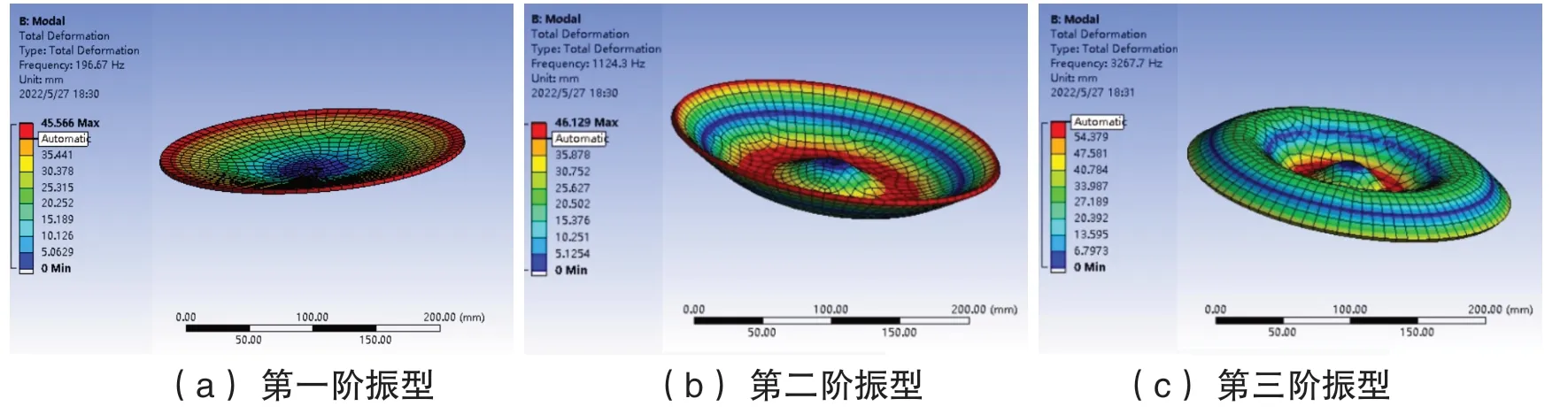
图3 圆盘弯曲振型

2 圆盘弯曲振动的实验测试

实验测试易产生无效的结果，第1 节已使用有限元方法预估了圆盘弯曲振动的固有频率和振型，本节将在有限元数值仿真结果的基础上进行实验测试，通过有限元结果挑选实验结果。固有频率测试有锤击法[13-14]、共振法[15]、超声振动测试法[10-11]等方法，锤击法具有实验设备简单、操作方便等优点，本文采用锤击法进行测试。实验设备及实验模型包括：振动实验台、金属圆盘、加速度传感器、冲击力锤、力传感器、动态数据采集仪、数据分析软件。图4 给出了实验设备和实验模型。

图4 实验装置及实验模型

采用单点拾振法进行测试，其实验原理和理论基础见文献[16-17]。受实验设备限制，本实验只能在64 个位置处敲击，敲击位置划分如下：以圆盘径向(120 mm)为第一坐标，进行四等分；以周向(360°)为第二坐标，进行十六等分；确定出64 个敲击点，即测点，图5 给出了测点的具体分布。P 点为拾振点，采用加速度传感器进行测量。采样频率选取2 560 Hz。触发模式为内触发，触发方向为上升沿，触发极性为正电平，触发电平20%，触发延时为-40，触发通道为力锤输入通道。

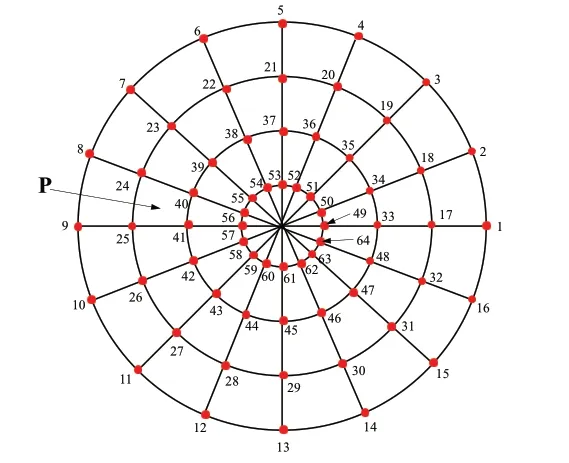
图5 测点分布

依次敲击64 个测点，得到拾振点的振动加速度。通过测试设备自带的模态分析软件进行初始估计，确定模态阶数；本测试选取12 个峰值进行拟合，见图6。通过模态计算和曲线拟合，可以计算出固有频率和振型函数。表1 给出了12 个点预估出的12 个频率值，其中含有非真实的频率和其他变形的振动频率。将实验测试结果与有限元结果作对比，寻找与有限元计算结果相近的测试频率，并观察其对应的振型图像，确定出真实的弯曲频率。表2 给出了2 种方法得到的前三阶固有频率，结果非常吻合。为验证实验测试频率的准确性，图7 给出了2 种方法所得的前三阶振型的对比图，其中上图为实验测试结果，下图为有限元结果。以圆心位置为参考，2 种方法所得的振型节圆个数一致，因而振型一致，有限元方法得到的振型图较为光滑，实验测试得到的振型图不太光滑，这主要是由实验敲击点偏少引起的。

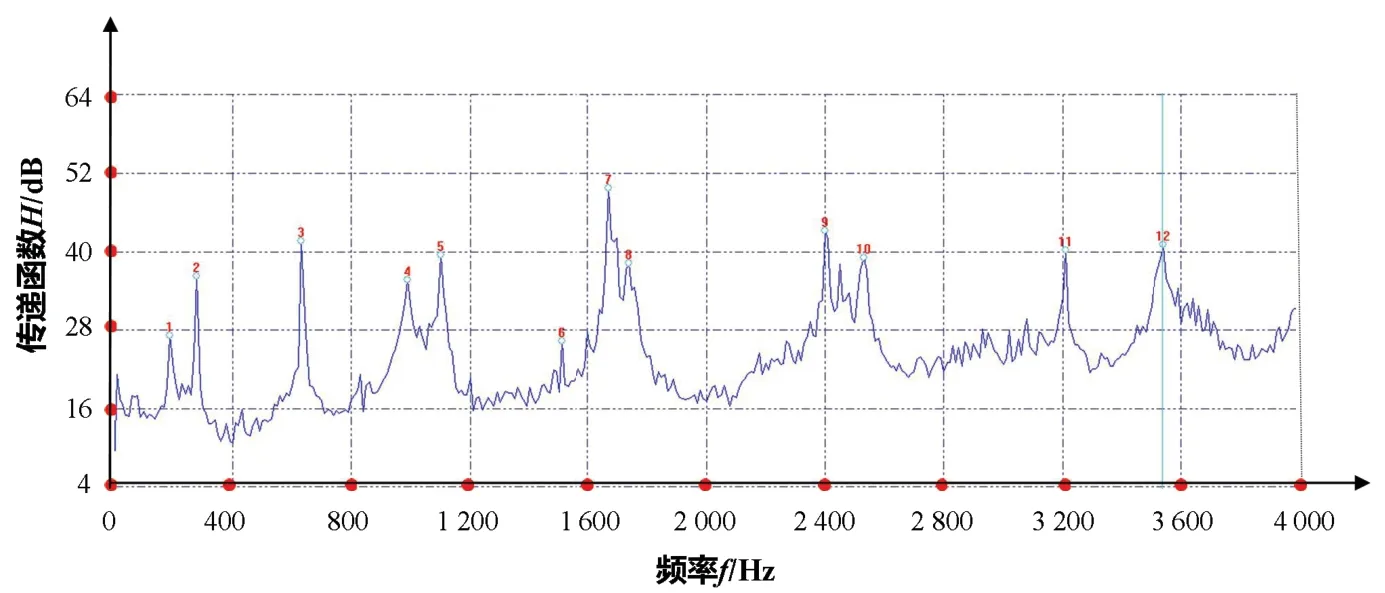
图6 初始估计选取的峰值

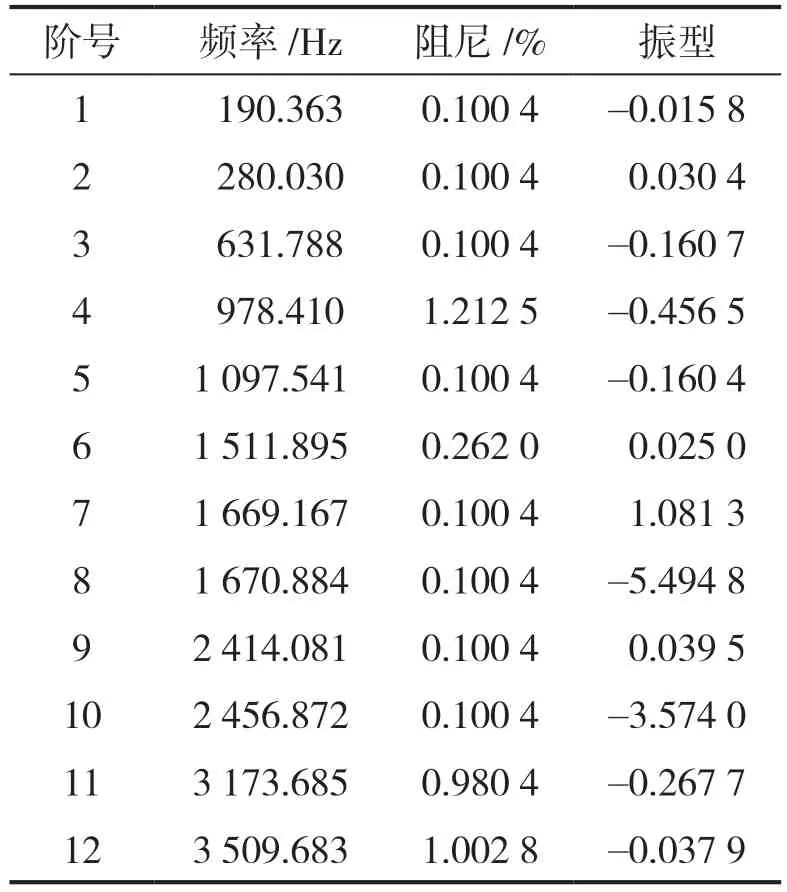
表1 实验测试的预估频率

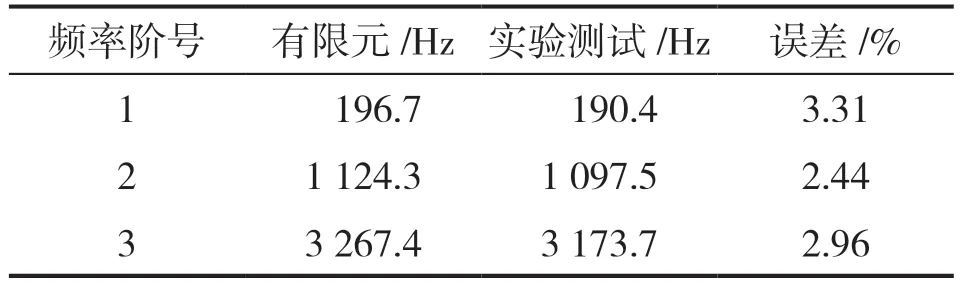
表2 两种方法所得频率的结果对比

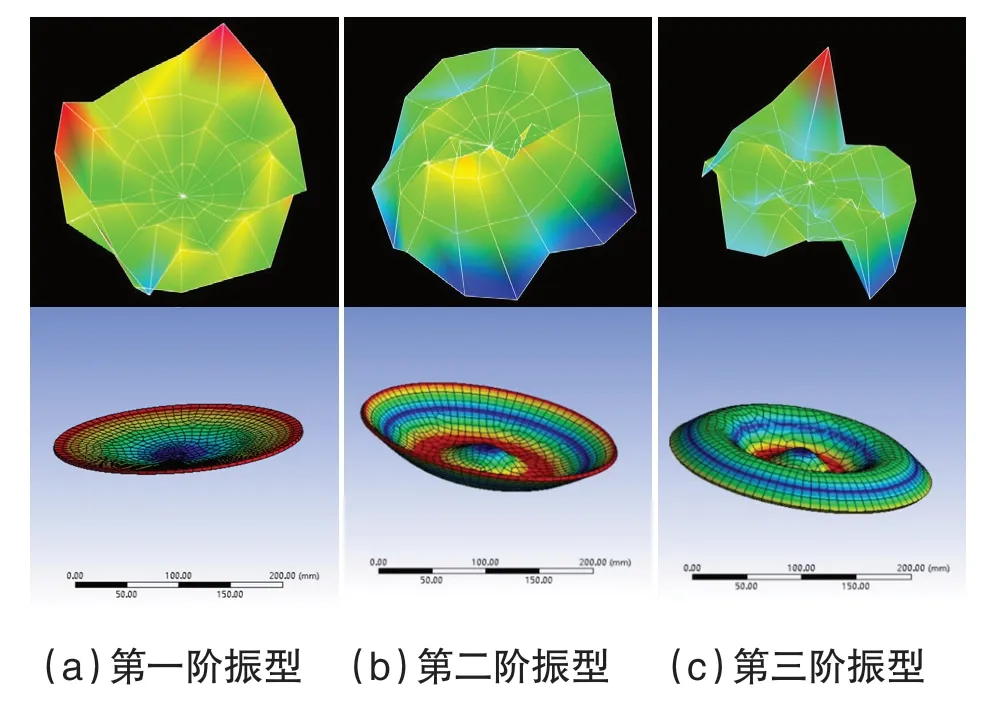
图7 圆盘弯曲振型实验测试（上图）与有限元结果（下图）对比图

3 结论

本文采用有限元数值仿真和实验测试相结合的方法研究了中心固支圆盘弯曲振动特性，首先采用ANSYS 有限元仿真软件对圆盘前三阶弯曲振动频率和振型进行了估算，得到如下结论：

（1）第一阶弯曲振型只在圆盘中心(即约束位置处)存在一个节点，圆盘上各点在节点的同一侧振动。

（2）第二阶弯曲振型除圆盘中心的节点外，出现了1 条节圆，节圆两侧的点沿不同方向振动。

（3）第三阶弯曲振型除圆盘中心的节点外，出现了2 条节圆，节圆两侧的点沿不同方向振动。

在有限元数值仿真的基础上，采用锤击法对圆盘弯曲振动特性进行了测试，测试采用多点敲击单点采集的方式进行，通过与有限元结果对比，从测试频率中选出弯曲振动频率，并对弯曲振型进行了对比。对比显示2 种结果非常吻合。