密闭空间内不同体积分数燃气爆炸特性研究

王丽敏，贾 虎，汪海波，陈 涛，宗 琦

（1.安徽理工大学 土木建筑学院，安徽 淮南 232001；2. 南阳师范学院 土木建筑工程学院，河南 南阳 473061）

城市综合管廊（Utility Tunnel）是埋设在道路下的一种可以容纳电力管线、给排水设施和燃气管道等市政管路的隧道空间。燃气管道的设置依据国家规范单独设置在一个舱室并安设防火门和报警系统[1]，燃气舱内照明系统按规范布置以减少燃气泄漏后发生爆炸事故[2]。若燃气舱的电力系统发生老化或漏电，则会造成燃气泄漏积聚后遇到明火发生局部爆燃。当密闭空间内大部分区域处于燃气爆炸极限的范围时，若气体遇火被引燃将会造成严重的爆炸事故，爆炸所产生的爆生气体和冲击波等破坏因素会造成道路系统瘫痪，以及对居民的生命财产造成巨大损害。因此，对密闭空间内燃气爆炸特性展开研究十分必要。

在密闭空间内气体爆炸数值模拟研究方面，高保彬等[3]利用Fluent 软件采用大涡模拟方法，在三维燃气舱中挡气板不同间距的情况下对预混甲烷体积分数为9.5%的燃气进行爆炸模拟，说明了超压峰值和挡气板间距的关系，挡气板可以减小冲击波在燃气舱中反射拉伸；陈胜朋等[4]采用有限元软件模拟了甲烷在二维圆面爆炸过程中的气流的变化情况，从而得出了在一定的条件下可用状态方程RNG 来描述受限空间可燃气体爆炸过程；毕明树等[5]对圆柱形容器进行了数值模拟，结果表明甲烷体积分数在接近9.5%时，火焰最大速度最大，爆炸最大压力最大，达到最大压力时间最小。在气体爆炸试验研究方面，余明高等[6]搭建简易气体爆炸试验平台对多种不同体积分数的预混气体的爆炸特性进行研究，得到产生的爆炸压力的变化总是先于火焰传播速度变化，因此减小爆炸压力和降低升压速率是抑制爆炸的关键；尉存娟等[7]利用水平管道式气体爆炸装置对5 种不同体积分数的甲烷进行爆炸实验，证明了甲烷体积分数越接近化学当量浓度时升压速率越大，甲烷体积分数偏离化学当量浓度越多，压力峰值时间增长的越为明显；吴建松等[8]、陈卓等[9]和邓成云等[10]开展了燃气爆炸传播特性试验研究，探究了管道内发生爆炸时爆炸冲击波的传播规律和火焰传播速率。

由于综合管廊的燃气舱属于密闭空间，一旦发生燃气泄漏，燃气会积聚形成混合气体，在温度适宜或遇明火时会发生爆炸。现有研究对于密闭空间不同体积分数燃气发生爆炸时的火焰传播特征、超压等特征的描述并不完整。研究采用Fluent 对密闭条件下不同燃气体积分数（8.3%、9.5%、10%、11%）的爆炸过程进行二维数值模拟研究，得到燃气体积分数对舱内气体爆炸火焰速度、爆炸压力、冲击波传播的影响，以期应用于实际工程，为综合管廊燃气舱抑爆提供理论依据。

1 数值模型与设置

1.1 几何模型及测点布置

以某综合管廊燃气舱一个200 m 防火分区为研究对象，建立综合管廊燃气舱内长度方向燃气爆炸二维数值计算模型。鉴于燃气管道内直径较综合管廊燃气舱尺寸小得多，在建模过程中忽略综合管廊中管道及管道架的影响，模型的上壁面为管廊上壁面，下壁面为燃气管道上壁面，长200 m，宽2.1 m，两侧为防火墙（门），考虑采用最不利于管廊内气体通风扩散的静风状态，设置测点的分布与点火位置如图1 所示。

图1 简化计算模型示意图

设置点火位置为直径0.1 m 的圆形，圆心坐标为X=0 m，Y=0 m 处。按照位置不同设置2 组监测点：

1）燃气舱中部：每间隔20 m 布设1 个测点、共5 个监测点，监测燃气舱中部燃气爆炸变化规律，其坐标分别为：X=-20 m，Y=0 m；X=-40 m，Y=0 m；X=-60 m，Y=0 m；X=-80 m，Y=0 m；X=-100 m，Y=0 m。

2）燃气舱顶部：每间隔20 m 布设1 个测点、共6 个监测点，分别为：X=-0 m，Y=1.05 m；X=-20 m，Y=1.05 m；X=-40 m，Y=1.05 m；X=-60 m，Y=1.05 m；X=-80 m，Y=1.05 m；X=-100 m，Y=1.05 m。

1.2 数学模型的建立

燃气爆炸的过程是一种甲烷的单步燃烧反应，流体的流动需要遵守的物理规律有质量守恒定律、动量守恒定律和能量守恒定律，取其相对应的守恒方程。同时研究的问题中还涉及到不同的组分（空气和甲烷） ，因此也要遵守组分守恒定律，并取其相对应的组分运输方程。

组分方程如公式（1）所示：

气体状态方程如公式（2）所示：

式中：ρ为流体密度，kg/m3；t 为时间，s;θa表示组分的体积浓度；Da表示组分的扩散系数；Sa表示组分的源项；R 表示燃气常数，J/（kg·k）；m 表示气体质量，kg；V 表示气体体积，m3。

1.3 模拟设置

（1）网格划分。利用ICEM 软件建立一个长200 m、宽2.1 m 的矩形模型，忽略管壁厚度，将模型中心网格划分长度为10 mm，剩余部分的网格大小采用呈梯度变化的结构化网格，在接近顶部壁面的网格进行加密，网格总数量为789 921 个，局部网格划分示意图如图2所示，最终经检验网格质量为0.9 以上，符合计算要求。

图2 局部网格划分示意图

（2）求解器设置。采用基于压力（Pressure-Based Solver）的求解方式，非稳态，RNG k-ε湍流模型，标准壁面函数。使用结合Arrhenius 公式和涡耗散方程的Finite-Rate/Eddy-Dissipation（有限速率/涡耗散模型）模型进行数值模拟。采用SIMPLE 算法进行迭代求解。步长0.001 s，步数1 400，迭代数30，计算1.4 s 内燃气舱爆炸过程。

（3）边界条件及初始条件。边界条件：模型的四周边界均采用无滑移绝热壁面，壁面粗糙度设为0.002 m，粗糙常数设为0.5。初始条件：分别对综合管廊燃气舱内甲烷体积分数为8.3%、9.5%、10%、11%的甲烷-空气预混气体进行数值模拟。空气中的气体包括氧气、氮气、二氧化碳和其他稀有气体，其中氧气和氮气占比较大，氮气的体积分数约为78%，氧气的体积分数约为21%，因此这里忽略其他气体假设管廊中仅含有甲烷、氧气、氮气三种，各气体的成分比例见表1。

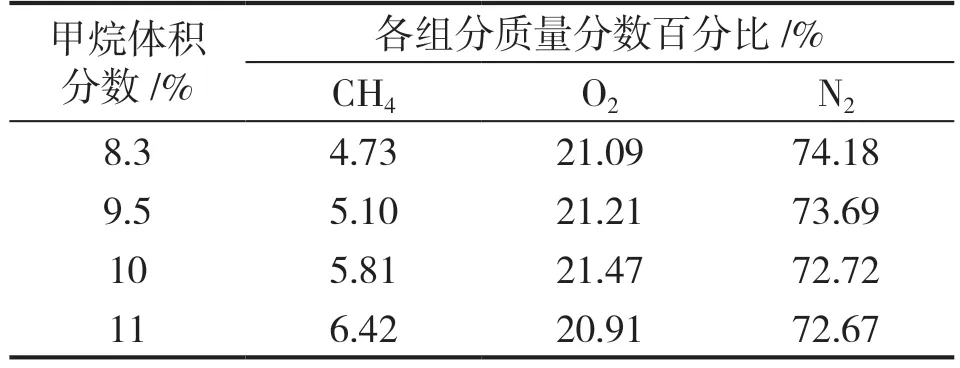
表1 不同CH4 体积分数预混气体的成分比例

假定初始气体混合均匀并均处于静止状态，初始压力为大气压力，初始温度为300 K。在燃气舱的中心坐标为（0，0）位置处设置直径为0.1 m 的圆形高温区，初始压力P=1 000 KPa，初始温度T=2 000 K，根据CH4体积分数不同分别设置CO2质量分数为0.148、0.152、0.159、0.165，H2O 质量分数为0.119、0.12、0.13、0.14。

（4）计算假设。在CFD 模拟软件中，物质的性质是根据模拟环境来设定其相应的条件后输入的。但在实际情况下，管廊内燃气发生爆炸后，舱内环境是持续变化的过程。研究重点关注舱室内发生爆炸后火焰扩散情况及超压影响。同时避免问题的复杂化，在满足工程精度的条件下，对数值模拟作出如下假设：

① 燃气爆炸为甲烷气体单步不可逆反应；

② 将燃气视为可压缩理想气体；

③ 燃气体积分数按照8.3%、9.5%、10%、11%四种工况混合均匀充满舱内。

2 模拟结果与讨论

2.1 燃气舱火焰燃烧速度变化规律

计算得到不同条件下火焰传播特征，对比火焰形态，给出燃气体积分数为9.5%不同时刻火焰传播范围如图3 所示。

图3 燃气体积分数为9.5%时不同时刻火焰传播范围

每个测点的火焰燃烧速度变化规律大致相同：在点火区域温度上升周围燃气被点燃，初期阶段火焰以光滑球形阵面向四周传播，燃烧速度缓慢上升；火焰加速阶段火焰阵面发生褶皱，形状由球形拉伸为锥形，燃烧速度急速增大如图3中0.42 s 所示，这是由于管廊内温度升高气体体积膨胀，使得压强增大，此时火焰传播速度由燃烧波速度和膨胀气体推进速度共同叠加作用；火焰峰值阶段的火焰形状如图3 中0.61 s 所示呈现郁金香形，燃烧速度达到最大；火焰减速阶段由于前期冲击波传播至管廊防火门端产生反射冲击波，此时已燃区的压强减小，点火源附近气体收缩，气体推进速度变为负值，导致燃烧速度下降直至燃气被完全耗尽。

由于点火点位于燃气舱中心点且模型具有对称性，火焰燃烧通过点火中心部位向两侧传播，得到两侧数据高度吻合，因此取点火点左侧中部测点来描述火焰燃烧速度的变化规律，得到在测点3 处火焰燃烧速度最大，图4 为测点3 处不同燃气浓度火焰燃烧速度时程曲线。

图4 不同燃气体积分数火焰燃烧速度时程曲线

由图4，火焰燃烧速度随时间增加呈先增大后减小的趋势，在燃烧初期（0～0.14 s）燃气体积分数10%和11%的火焰燃烧速度相似，燃气体积分数为11%的火焰燃烧速度在0.1 s 处与9.5%相差最大为17.6 m/s，与8.3%相差最大为23.2 m/s；在0.14 s 之后燃气体积分数为9.5%的燃烧速度加速增大，以最大的速率最先到达峰值，9.5%的燃气体积分数火焰燃烧速度在t = 0.44 s 时能达到最大为V峰（9.5%）=275 m/s，10% 的燃气体积分数火焰燃烧速度在t=0.451 s 时达到最大为V峰（10%）=256.5 m/s， 比9.5% 小18.5 m/s，11%的燃气体积分数火焰燃烧速度在t=0.458 s 时能达到最大为V峰（11%）=249 m/s，比9.5%小26 m/s，8.3%的燃气体积分数火焰燃烧速度在t=0.47 s 时能达到最大为V峰（8.3%）=219 m/s，比9.5% 小56 m/s。4 个体积分数相比达到峰值所用时间顺序：t（9.5%）< t（10%）< t（11%）< t（8.3%）。燃气体积分数为9.5%时率先在t=0.91 s 完成燃烧反应，其次分别为10% 在t=0.98 s、11% 在t=1.01 s、8.3%在t=1.15 s 时各自完成燃烧反应，9.5%达到时间比10%早0.07 s，比11%早0.1 s，比8.3%早0.24 s。

进一步得到不同燃气体积分数最大火焰燃烧速度曲线，如图5 所示。可见，最大燃烧速度随燃气体积分数增大呈先增大后减小的趋势即V(9.5%) > V(10%) > V(11%) > V (8.3%)。 这是因为燃气体积分数为9.5%时发生燃烧爆炸反应，气体分子碰撞率和燃烧反应速率达到最大，即单位时间内所产生的热量达到最大，在剧烈的燃烧反应和高产的热量加持下使得火焰向前推进的速度增长迅速，最终导致燃气体积分数为9.5%时燃烧速度最大。

图5 不同燃气体积分数最大火焰燃烧速度

2.2 燃气舱超压随时间的变化规律

综合管廊燃气舱内燃气被点燃后会产生前驱冲击波及火焰压缩波，火焰压缩波在点火点以球形波向外扩展传播，前期火焰阵面燃烧速度较小由此释放的能量也相应较小，因此所产生的前驱冲击波前期相对较小，但是在继前驱冲击波之后所伴随的稀疏波及压缩波的作用下，燃气爆炸超压数值在初期会以小幅波动但接近平滑的状态逐渐增大。由于燃气舱两侧设置防火门位置，冲击波率先到达两侧会因壁面反射叠加作用产生一个与其反向的反射波，反射波与前驱冲击波后的火焰压缩波相互叠加，致使燃气爆炸出现第一个峰值，随着压缩波及反射波传播的继续，超压时程曲线发生震荡。图6 为9.5% 燃气体积分数在燃气舱内发生爆炸0.42 s 至0.48 s 时超压的变化云图。

图6 9.5%燃气体积分数燃气舱超压变化云图

图6 表明燃气舱内的超压随着时间呈现先增大后减小再增大的趋势，在0.48 s 时冲击波达到两侧壁面，在两侧壁面时冲击波传播速度达到最大。由于不断地反射叠加，会逐渐降低其自身能量，最终燃气爆炸超压值趋于一个稳定值。

不同燃气体积分数燃气舱中部、顶部各测点超压随时间变化曲线如图7、图8 所示。不同燃气体积分数燃气舱中部与顶部各测点超压随时间变化的规律相似，初期接近平滑状态增大随后出现锯齿状波动最终趋于稳定。但是图中能看出每种燃气体积分数在燃气舱顶部测点的超压略较中部的大，这是由于火焰压缩波最先到达燃气舱上下壁面并反射叠加，最终导致顶部超压大于中部超压：燃气体积分数 为8.3% 时在 测 点1、2、3、4、5 处顶 部 超压比中部超压分别大0.084 MPa、0.111 MPa、0.099 MPa、0.089 MPa、0.092 MPa；燃气体积分数为9.5%时在测点1、2、3、4、5 处顶部超压比中部超压分别大0.114 MPa、0.131 MPa、0.122 MPa、0.107 MPa、0.095 MPa；燃气体积分数为10%时在测点1、2、3、4、5 处顶部超压比中部超压分别大0.082 MPa、0.103 MPa、0.104 MPa、0.106 MPa、0.099 MPa；燃气体积分数为11%时在测点1、2、3、4、5 处顶部超压比中部超压分别大0.082 MPa、0.099 MPa、0.093 MPa、0.083 MPa、0.094 MPa。可知，在测点2 位置顶部超压与中部超压相差最大，但相差不超过0.131 MPa。

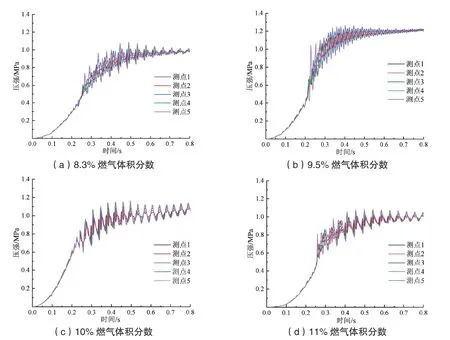
图7 燃气舱中部各测点超压-时间变化曲线

图8 燃气舱顶部各测点超压-时间变化曲线

不同燃气体积分数在测点11 处最大超压分布曲线如图9 所示。

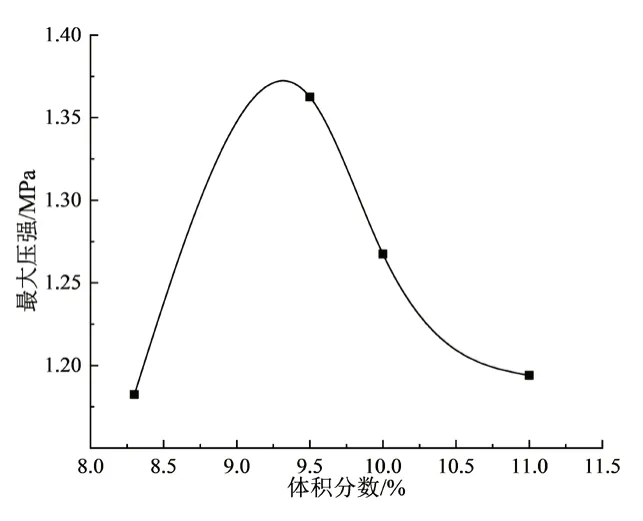
图9 不同燃气体积分数在测点11 处最大超压分布曲线

由图9 所得最大压强随燃气体积分数增加呈先增大后减小的趋势，其中Pmax（9.5%）>Pmax（10%）>Pmax（11%）>Pmax（8.3%）。当燃气体积分数为9.5%时，冲击波和压缩波在相同的时间内反射叠加的次数最多，超压时程曲线发生震荡相隔时间最短，爆炸压强峰值最大可达1.37 MPa，其他测点也遵循这一规律，说明了当燃气体积分数为9.5%时燃烧爆炸反应发生最为完全，能量释放达到最高，所产生的爆炸超压值最大。得到各测点最大超压分布曲线如图10 所示。

图10 不同燃气浓度各测点最大超压分布曲线

由图10 可得各燃气体积分数爆炸最大超压随着与点火点位置距离的增加出现先减小后增大的趋势，在距离点火点100 m 处的防火门处超压值最大。9.5%燃气体积分数不同测点的最大超压在1.20～1.35 MPa 之间，10%燃气体积分数不同测点的最大超压在1.10～1.25 MPa 之间，11%燃气体积分数不同测点的最大超压在1.02～1.16 MPa之间，8.3%燃气体积分数不同测点的最大超压在1.00～1.15 MPa 之间，各体积分数不同测点最大超压的变化在0.15 MPa 左右，11%和8.3%燃气体积分数最大超压变化最为接近。

图11 为不同燃气体积分数最大升压速率分布曲线，图中最大升压速率在燃气体积分数为9.5%时最大可达到3.49 MPa/s，在一定范围内向两侧递减即：△p9.5%＞△p10%＞△p11%＞△p8.3%。这表明在燃气体积分数小于9.5%时燃气爆炸升压速率受燃气体积分数影响较大，当燃气体积分数大于9.5%时影响较小。在9.5%两侧最大升压速率随燃气体积分数的变化近似呈线性关系，因此以爆炸升压速率可直接反映爆炸强度。

图11 不同燃气体积分数最大升压速率分布曲线

图12 为不同燃气体积分数达到最大压强、最大燃烧速度出现的时间分布曲线，可得到以下规律：

图12 最大爆炸压强和燃烧速度出现的时间

（1）不同体积分数燃气在密闭定容爆炸模拟中最大压强及最大燃烧速度所出现的时间不同，均在体积分数为9.5%时出现最早，以9.5%为中心各曲线均在9.5%之前变化梯度比较大，接近直线上升，而在9.5%之后变化梯度较小，呈缓慢下降，这表明各峰值出现的时间在9.5%前受体积分数影响较大，在9.5%后影响较小。

（2）不同体积分数的燃气在发生定容爆炸时最大燃烧速度出现时间滞后于最大压强出现时间，其原因为当发生燃气爆炸时火焰从模型的点火点处向两端传播从而产生大量热，从而使气体膨胀导致测点的压强增大，已燃区与未燃区的压强差使得火焰锋面向前，因此最大压强和最大燃烧速度出现时间分布曲线形状类似，但出现的时间有先后顺序且不同燃气体积分数各参数滞后时间相差不大，所以两曲线走向近似平行。可知，在充满燃气的密闭空间中点火点条件相同的情况下燃气体积分数直接影响着爆炸压强和燃烧速度，且各浓度燃气爆炸压强对火焰的燃烧速度有促进作用。

3 结论

采用Fluent 有限元软件对综合管廊燃气舱密闭空间内充入不同体积分数的燃气后点火爆炸进行了数值模拟，得到了如下结论：

（1）在燃气体积分数为8.3%～11%的范围内的燃烧速度近似成二次函数关系，在燃气体积分数为9.5%时火焰燃烧速度最大可达到267 m/s，燃烧用时最短为0.91 s，燃烧反应最剧烈。

（2）各测点爆炸超压存在不同峰值，随着距点火点距离的增加呈先降低后增大，在防火门处超压峰值达到最大。火焰的冲击波最先到达计算模型的上下壁面并发生反射叠加导致顶部测点压强值略大于中部测点，在测点2 位置顶部超压与中部超压相差最大，但相差不超过0.131 MPa。随着燃气体积分数的增加爆炸产生的最大升压速率、爆炸压强和燃烧速度呈先增大后减小的趋势，在9.5%两侧最大升压速率随燃气体积分数的变化近似呈线性关系，因此以爆炸升压速率可直接反映爆炸强度。

（3）不同燃气体积分数最大燃烧速度出现的时间总是略滞后于最大压强出现的时间，充满燃气的密闭空间中点火点条件相同的情况下，燃气体积分数直接影响,爆炸压强和燃烧速度，爆炸压强对燃烧速度也有一定的影响，可以通过减小爆炸压强限制爆炸火焰燃烧的传播速度从而达到抑爆的效果。