一种考虑孤岛运行和可再生能源出力不确定性的有源配电网供电可靠性分析方法

朱良管，曾平良，刘恺诚，丰俊杰

(1.杭州电子科技大学自动化学院，杭州 310000; 2.中国电力科学研究院有限公司，北京 100080;)

0 引言

为应对气候变化和环境无染，近年来，以风电、光伏为代表的分布式可再生能源发展迅速，截止2019 年底，我国风电、光伏装机容量分别到达210 GW 和205 GW，其中分布式风电和光伏占总装机的25%左右，稳居世界第一。随着可再生能源渗透率的不断提高，近几年来，我国弃风弃光严重，2016 年，我国弃风和弃光电量分别达到497 亿kW·h 和74 亿kW·h，严重阻碍了可再生能源的发展，是亟需解决的关键技术问题之一。发展分布式电源是解决可再生能源消纳和高比例清洁能源发展的重要措施，近几年来，分布式电源得到了世界各国的高度重视而获得了快速发展。分布式电源一般指在用户侧配置的功率较小的发电机组，用来满足一些重要负荷的用电需求，目前典型的分布式电源技术有光伏、风力、小型燃气机组等。由于分布式可再生电源的灵活性、环境友好性等特点，越来越多的分布可再生电源被接入配电网，它使配电网更加灵活，但是，分布式可再生电源固有的间歇性和随机性，对原有配电网的结构和运行带来了新的挑战。因此，研究分布式可再生电源并网后对配电网的可靠性影响至关重要。文献［1-3］采用了最小割集法评估了分布式电源接入后配电网的可靠性，该方法适用于评估复杂的配电网结构。文献［4-5］采用了馈线分析法，该方法能够得到各个馈线供电区域的可靠性指标，提高评估效率。文献［6-7］采用了网络等值法，求解出配电网区域的故障影响模式分析表，该方法的概念简单，求解容易，但是其得到的是中间结果，若要求取最终状态，计算过程较为复杂。文献［8］采用状态空间法，得出了分布式电源并网后，配电网可靠性指标的变化，但是如果配电网的结构较为复杂，元件较多时，该方法将不再适用。

文中提出一种考虑孤岛运行和可再生能源出力不确定性的有源配电网供电可靠性分析方法。首先基于两状态马尔科夫模型建立了配电网设备的可靠性模型;其次，可再生能源场站的出力可靠性模型是由场站设备状态和可再生能源潜在出力概率组成，进而建立了考虑场站设备可靠性的可再生能源场站多状态模型;然后，利用馈线分区的概念划分孤岛运行范围，分析孤岛运行对供电可靠的影响; 最后再结合序贯蒙特卡洛分析方法求得有源配电网供电可靠性。利用IEEE 测试系统对所提方法进行验证，证明方法的准确性。

1 有源配电网可靠性模型

1.1 配电网设备可靠性模型

配电网由各种配电设备组成，元件是配电网可靠性评估的最小单元，假设其中大部分元件都可以被修复，例如: 配电线路、断路器、熔断器、自动重合闸开关等，因此，配电网元件的可靠性评估模型可采用马尔科夫两状态模型，只需要考虑其正常运行状态和故障修复状态［9-10］，如图1 所示，λ 代表元件的故障率，μ 代表元件的故障修复率。

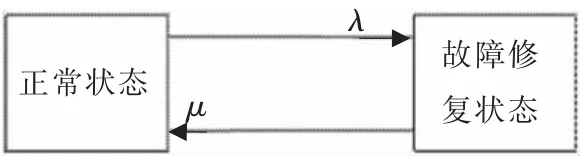
图1 元件的两状态可靠性模型Fig.1 Two-state reliability model for components

元件的两状态模型如式( 1) 和式( 2) 所示，其中MTTF表示元件平均正常运转时间，MTTR表示元件平均故障修复时间。

由于配电网设备元件的故障是随机发生的，设TTF为配电网元件正常工作时的运行时间，TTR为配电网元件的故障修复时间，TTF与TTR随时间的变化而变化，MTTF与MTTR分别为TTF与TTR的平均值，图2 模拟了配电网元件TTF与TTR的循环过程。

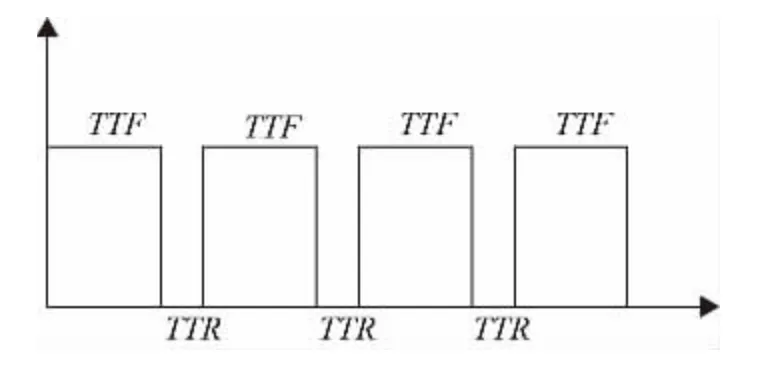
图2 TTF 与TTR 的循环过程Fig.2 Cycle process of TTF and TTR

在配电网可靠性分析中，通常认为配电网设备元件不具备记忆性，即元件任意两次故障之间没有关联性，假设元件故障率λ 和修复率μ 服从指数分布，如式(3)所示:

式中f(t) 为t时刻元件故障的概率，g(t) 为在t时刻元件故障修复的概率。元件正常工作时间和故障修复时间的概率分布函数，如式(4) 所示:

对式(4) 进行求导变化，可得式(5) 为:

式中F'(t) 表示元件正常工作时间为t的概率;G'(t) 表示元件故障修复时间为t的概率。F'(t) 和G'(t) 都是［0-1］之间的数，通过随机抽样也可以产生［0-1］的数，进一步可以将其转化为服从指数分布的随机数，因此元件正常工作的时间TTF，元件的故障修复时间TTR可以表示为式(6) :

式中Rt1和Rt2为计算机产生的［0-1］的数。

1.2 考虑设备可靠性的分布式可再生能源多状态模型

1.2.1 分布式可再生能源多状态模型

可再生能源场站的出力可靠性由场站设备状态和可再生能源潜在出力概率分布组成。可再生能源潜在出力( Renewable Energy Potential Output，REPO) 为可再生能源场站将风光等自然资源转换成电能所发出的功率，取决于风光等资源情况，具有较强的随机性。对于场站设备可靠性，文中采用基于马尔科夫的两状态模型，即正常运行状态和故障状态，假设分布式可再生电源场站设备故障率为λ，修复率为μ，分布式可再生电源场站设备正常工作时间TTFres和故障修复时间TTRres可由式(6) 得出。

针对风光等可再生资源固有的间歇性和随机性，REPO 可用多状态模型进行描述，状态数量一般取决于风光等资源特征和可靠性分析精度。因此分布式可再生能源场站的多状态模型由场站设备和REPO 多状态模型联合组成，如式(7) 所示:

式中S 表示可再生能源场站多状态矩阵;n为REPO 状态数;ρi为REPO 状态i的概率。可再生能源场站多状态模型如图3 所示。

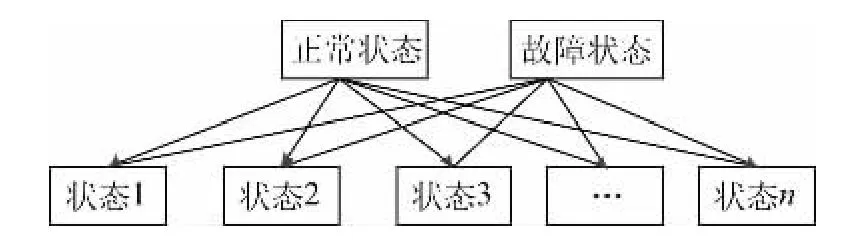
图3 可再生能源场站多状态模型Fig.3 Multi-state model of renewable energy station

由式( 7) 可知，在场站设备故障状态下，无论REPO 处于哪种状态，可再生能源场站输出功率都为0，因此，式(7) 可以进一步简化，如式(8) 所示:

式中，Si表示可再生能源第i个状态，i=1 时，为分布式电源场站出力为0 的概率。

1.2.2 分布式光伏REPO 多状态模型

分布式光伏发电系统的潜在出力特性取决于光照强度、太阳能光伏阵列的温度等因素，其中光照强度是光伏出力的主要因素，本文只考虑光照强度对光伏出力的影响，光伏出力曲线与光照强度的关系如图4 所示［11］。

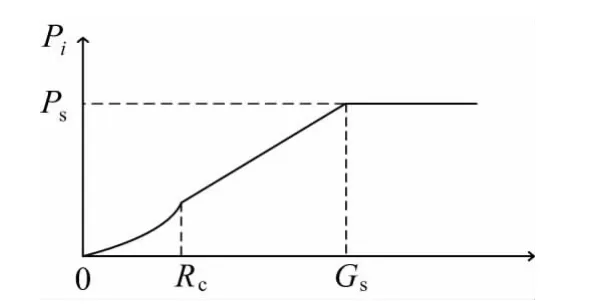
图4 光伏发电系统的出力曲线Fig.4 Output curve of photovoltaic power generation system

光伏发电系统的输出功率可用分段函数近似表示，如式(9) 所示:

式中Pi表示光伏系统的发电功率( MW) ;Ps为光伏阵列的额定功率( MW) ;Gi表示第i时刻的光照强度( W/m2) ;Gs表示在标准环境下的光照强度，一般取1000 W/m2;Rc表示一个特定大小的光照强度，通常取150 W/m2。

考虑夜间没有光照以及白天光照受云层等随机因素影响，光照强度分布一般可用β 分布来描述，如式(10) 所示［12］。

式中Г(z) 为Gamma 函数，α，β 为参数，可以通过对历史光照数据进行拟合获得。x为光照强度与标准环境下的光照强度之比，即:x=G/Gs。

光照强度的累计概率分布为［13］:

式中Bx( α，β) 为不完全β 函数;Ix( α，β) 为正则不完全β 函数。正则不完全β 函数的累计概率为1。

从式(9) 、式( 11) 可以看出，对应每一个光照强度，可以得到相应的光伏出力和累计概率。通过式(9)把相应的光照强度转化为光伏出力，可以从式( 11) 获得光伏出力为P的累计概率分布，即:

式中ω(P;α，β) 为光伏出力累积概率分布函数;xaP表示把光照强度x通过式(9) 转化为光伏出力P。

为提高计算效率，可把光伏出力曲线简化为n个离散功率来表示，每个功率Pi代表光伏的一个出力状态。则光伏出力状态为Pi的概率为:

式中n为光伏出力状态数。

光伏出力状态个数由光伏电站所在区域的光资源特性、可靠性分析精度要求等因素决定。文中设n=5，从而得到光伏REPO 5 状态模型，随着光照强度的不断变化，各个状态之间可相互转化，如图5 所示。当光照强度大于等于标准光照强度时，光伏达到最大出力，此时如果光照强度发生变化，如云层遮掩，光伏出力将会降低，即从状态5 转移到状态4，但是，值得指出的是即使受云层影响，由于光照强度的变化是连续的，光伏出力不能从最大跃变为0，也就是说不能从状态5 直接转移到状态1，同样，光伏出力不能从状态1 直接转移到状态5，因此5 个状态之间不能形成一个闭环。这对采用不同状态个数的光伏可靠性模型同样适用。

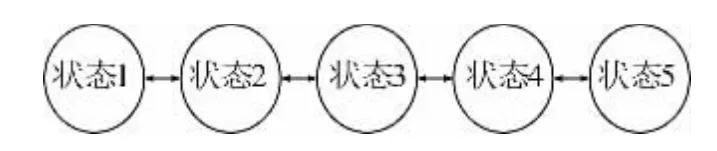
图5 光伏系统五状态模型之间的转化关系Fig.5 Conversion relationship between five-state models of photovoltaic systems

1.2.3 分布式风电场REPO 多状态模型

分布式风电厂出力受风速等自然因素影响。目前，风速概率模型主要有威布尔分布、卡方分布、正态分布等，其中两参数的威布尔分布应用较为普遍，本文采用两参数威布尔函数来描述风速分布。威布尔分布的概率密度及累计概率分布函数分别为式(14) 和式(15) 。

式中k为威布尔分布的状态参数; λ 为尺度参数，反映了风电场的平均风速。计算k和λ 方法有很多，其中主要有HOMER 软件法，平均风速和最大风速估计法、最小乘法等。

风电机组出力的大小主要取决于风速的大小，同时风速具有明显的随机性，风电机组的输出功率与风速之间曲线如图6 所示［14］。

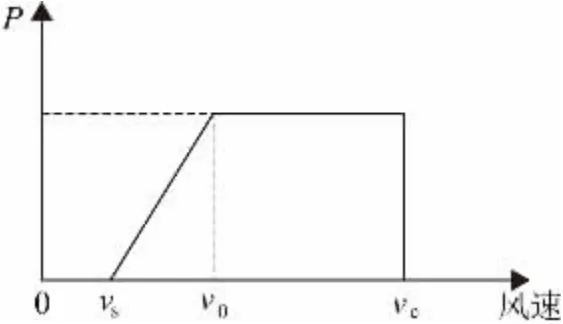
图6 风电机组的输出功率与风速之间的关系Fig.6 Relationship between the output power of a wind turbine and wind speed

风电机组的输出功率与风速之间的表达式可近似表示为:

式中Pv为风电机组的输出功率;vs为风机的启动风速;vo为额定风速;vc为切除风速;Pc为风电机组的额定输出功率。

与1.2.2 节光伏出力多状态模型的推导相类似，风电出力累计概率分布函数为:

式中ζ(Pv;λ，k) 为风电出力累计概率分布函数;vaPv为风速v通过式(17) 转化为风电出力Pv。

当风速大于切出风速vc时，风电出力为0，其概率为:

与光伏REPO 多状态模型相类似，可把风电场REPO 出力简化为由n个离散功率来表示，每个功率代表风电场的一个出力状态，即n个出力状态。则风电场出力状态为Pi的概率为:

当i=1 时，风电出力为0，其概率由风速小于切入风速和大于切出风速两部分概率组成。

风电出力状态个数与风电场风资源特性和可靠性分析精度要求有关。设n=5，得到风电出力5 状态模型，如图7 所示。

可以看出，当风电处于状态5 时，随着风速减小，风电出力将由状态5 向状态4 转移，另一方面，当风速增大，超过切出风速时，风电出力将由状态5 向状态1转移，即从最大出力变为0。值得指出的是，风电出力不能由状态1 向状态5 转移，因为风速具有连续性。因此，风电出力状态之间形成一个闭环转移关系。这是和光伏出力多状态模型不同的地方，是由光伏、风电系统运行特性不同所造成的。

2 孤岛运行方式

当分布式可再生电源并网后，改变了传统配电网的模式，使原有的单电源辐射网络结构转化为多电源网络结构，同时分布式可再生电源与负荷之间的直接相连，使配电网产生了一种新的运行方式—孤岛运行［15］，孤岛运行可分为计划孤岛与非计划孤岛，我国电网公司严格规定不允许非计划孤岛的出现，因此本文所述的孤岛运行模式是一种不间断供电的计划孤岛运行模式，在该孤岛运行模式下，当配电系统中的元件产生故障时，分布式电源不会被解列，而是通过瞬间跳开联络开关，形成孤岛，孤岛内分布式电源能够继续为部分负荷提供所需的电量，此时，孤岛运行过程中的输出功率与孤岛内总负荷的关系如式(20) 所示:

式中n为孤岛内布式可再生电源的总数;Pi为孤岛内第i个分布式可再生电源的输出功率;m为孤岛内负荷的总数;Lj为孤岛内第j个负荷的大小。

3 可靠性指标

在配电系统的可靠性评估中，主要通过可靠性指标来体现，按照评估对象的不同，配电网的可靠性指标通常包括负荷点指标和系统指标。负荷点指标主要用来评估系统中单个负荷点的可靠性程度，系统指标主要用来评估整个配电网系统的可靠性程度，它以负荷点可靠性指标为基础计算出来的。

负荷点可靠性指标主要包括［16］:

1) 负荷点平均故障率λ。

负荷点平均故障率指在统计时间内( 一般时间以年为单位) ，负荷点的停电次数的期望值，单位为次/年。

2) 负荷点年平均停电时间U。

负荷点年平均停电时间指在统计时间内( 一般时间以年为单位) ，负荷点因故障停运持续时间的期望值，单位为小时/年。

3) 负荷点每次故障平均停运持续时间r。

负荷点每次故障平均停运时间可以由负荷点平均故障率与负荷点年平均停电时间计算得出，单位为小时/次。

系统可靠性指标主要包括:

1) 系统平均停电频率指标( System Average Interruption Frequency Index，SAIFI) 。

式中λi为负荷点i的平均故障率;Ni为负荷点i的用户数，SAIFI的单位为次/( 户·年) 。

2) 系统平均停电持续时间指标( System Average Interruption Duration Index，SAIDI) 。

式中Ui为负荷点i的年平均停电时间;SAIDI的单位为小时/( 户·年) 。

3) 系统总电量不足指标( Energy Not Supplied，ENS) 。

式中Li为负荷点i的平均负荷，kW·h/年。

4) 系统平均供电可用率( Average Service Availability Index，ASAI) 。

5) 系统平均电量不足指标( Average Energy Not Supplied，AENS)

式中AENS的单位为kW·h/户。

4 考虑可再生能源出力不确定性的有源配电网可靠性分析方法

针对可再生能源出力不确定性的有源配电网可靠性分析，由于经典的蒙特卡洛法在抽样过程中，将配电网元件及风光出力状态看成是相互独立的。实际上配电网元件与风光出力的状态不是相互独立的，是按照状态转移矩阵从一个状态转移到另一个状态，具有一定的“时序”关系，例如，在元件故障之后，有一个修复时间，才能重新恢复到非故障或其他状态，而不是随机地直接从故障状态跃变到非故障状态，同样，风光出力从0 到最大值需要经过从状态1 至状态2…至状态5的转移过程，而不能随机地从状态1 跳跃至状态5。而序贯蒙特卡洛方法能够根据状态转移关系矩阵对各状态进行准确抽样，可靠性评估结果比经典蒙特卡洛方法更准确，更符合实际。因此文中采用序贯蒙特卡洛模拟法评估，具体的评估流程如下:

1) 根据所选择的配电网的网络结构，读取相应的参数，形成8760 h 的负荷等级水平，确定仿真年数，设定初始时间为0;

2) 假设系统中元件处于正常工作状态，对系统中的非电源元件产生一个［0-1］之间均匀分布的随机数，将其转化为元件的正常工作时间TTF;

3) 通过比较步骤2) 随机产生非电源元件的无故障工作时间TTF，找到最小的TTFmin，此时将时间步长推进到TTFmin;

4) 对步骤3) 找到的元件，随机产生一个［0-1］之间均匀分布的随机数，并将其转化为元件的修复时间TTR;

5) 根据所选的测试系统，寻找受故障元件影响的其他负荷点，并判断这些负荷点是否处于孤岛内。是就执行步骤6) ，否则跳转到步骤7) ;

6) 如果负荷点是否可以通过孤岛运行继续为其供电，在孤岛运行过程中，根据可再生电源的随机处理的特点，需要每小时产生一个［0-1］之间均匀分布的随机数，确定此时孤岛内分布式电源总的输出功率P与孤岛内总的负荷水平L，如果P＞L，负荷点不会停电，如果P＜L，就按照负荷等级的重要程度进行削减负荷，直到满足P＞L为止，并且统计孤岛内负荷点的正常运行时间TTF与故障时间TTR;

7) 如果负荷点不可以通过孤岛运行继续为其供电，统计其正常运行时间TTF与故障时间TTR;

8) 判断总的模拟时间是否大于模拟年数乘以8760个小时，如果是就执行步骤9) ，否则跳转到步骤2) ;

9) 计算可靠性指标。

上述流程下，文中的蒙特卡洛模拟法的流程图，如图8 所示。

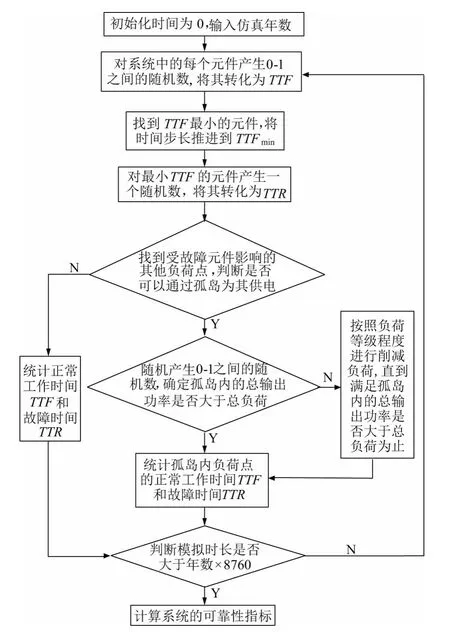
图8 蒙特卡洛模拟法的流程图Fig.8 Flow chart of Monte Carlo simulation method

5 仿真案例

文中采用的是改进的IEEE RBTS Bus6 系统，包括一条33 kV 的母线，30 条馈线、23 个负荷，10 个断路器，5 个分布式电源，为了表明方法的普遍适用性，光伏和风电可以分布在测试系统中所标注的DG 上，若干个隔离开关等，如图9 所示。

1) 系统中元件的故障率:馈线故障率为0.056 次/( 年·km) ，开关的故障率为0.005 次/年，平均修复时间都为3 h，表1 为系统给出的各个馈线的长度。

表1 馈线段长度Tab.1 Length of feeder section

2) 光伏系统数据我国某地区一年的光照强度分布如图10，根据1.2.2 节模型，假设光伏阵列的故障率λ 为3%，额定功率选为10 kW，标准光照强度Gs选取为1000 W/m2，特定光照强度Rc为150 W/m2，可得分布式光伏REPO 5 状态出力概率分布曲线如图11，具体值如表2 所示。

表2 光伏系统五状态模型Tab.2 Five-state model of photovoltaic system

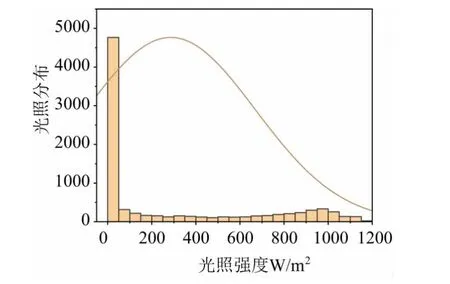
图10 某地区一年的光照强度分布图Fig.10 Annual illumination intensity distribution of a certain region

图11 光伏5 状态出力概率分布曲线Fig.11 PV five-state output probability distribution curve

3) 风电数据是我国某地区一年的风速，其概率分布如图12 所示。风电机组的设备故障率为2%，额定功率为1 MW，切入风速为4 m/s，切出风速为25 m/s，额定风速为10 m/s，则风电场REPO 5 状态出力概率曲线如图13，具体值如表3 所示。

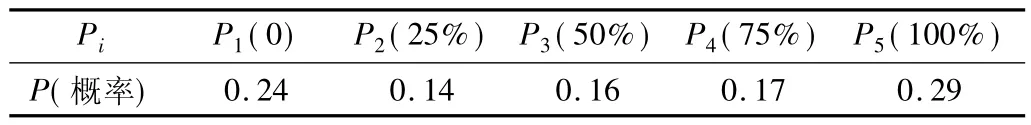
表3 风机出力五状态模型Tab.3 Five-state model of wind turbine output

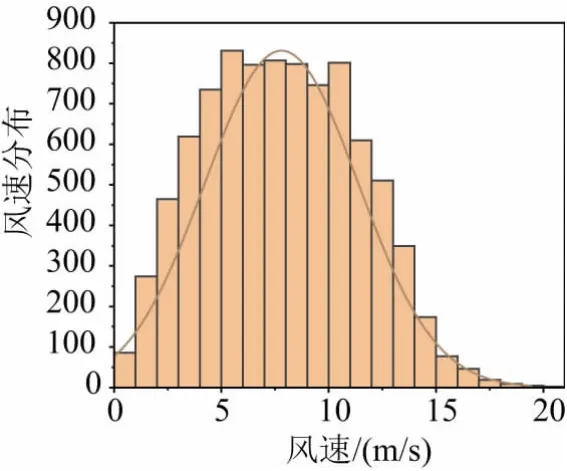
图12 某地区一年的风速分布图Fig.12 A yearly wind speed profile of an area

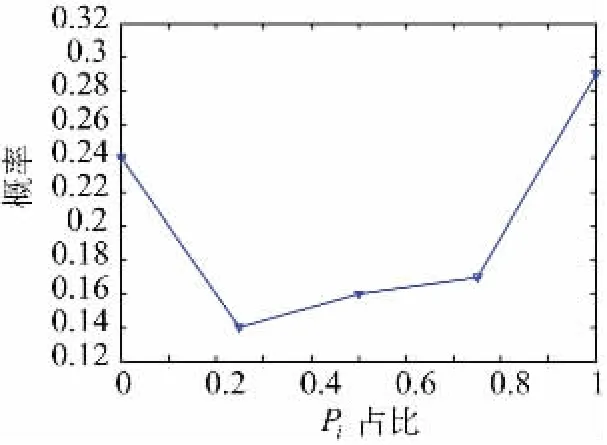
图13 风电5 状态出力概率分布曲线Fig.13 Probability distribution curve of wind power five-state output

4) 本文结合馈线分区的概念来处理孤岛内功率和负荷的关系，如测试系统图9 所示，假设LP7 故障时，断路器6、断路器19 和隔离开关11 进行动作来隔离故障同时恢复非故障区域的供电，由于断路器6 的动作使得LP-LP5 区域，不受故障的影响，能够正常供电; LP6-LP7 区域为故障区，停电时间为故障修复时间; 由于断路器19 的保护动作，使得LP14-LP18 区域形成计划孤岛，孤岛内运行的状态就需要根据式来判断是否需要削减负荷，当前孤岛内总负荷大于总出力时，就需要根据表负荷点的峰值与权重指标进行负荷的削减; 由于隔离开关11 的保护动作，使区域LP8-LP9、LP11-LP13、LP19-LP21 和LP22-LP23 形成了一个大范围的计划孤岛，孤岛的运行机制与LP14-LP18 区域相同。

测试系统图中的23 个负荷点的负荷点的峰值与权重指标，负荷点的权重指标表示负荷的重要的程度，一般超过0.5 表示重要负荷，如表4 所示。

表4 负荷点的峰值与权重指标Tab.4 Peak value and weight index of load point

为了确保评估结果的收敛性和准确性，本文将模拟时间设定为100 年，为分析分布式可再生电源接入对配电网可靠性的影响，文中考虑了分布式可再生电源接入配电网的两种场景，并对配电网可靠性指标进行了计算和比较。

1) 场景1:不考虑分布式可再生电源接入;

2) 场景2:考虑分布式可再生电源接入。

两种场景的分析结果如表5 和表6 所示。

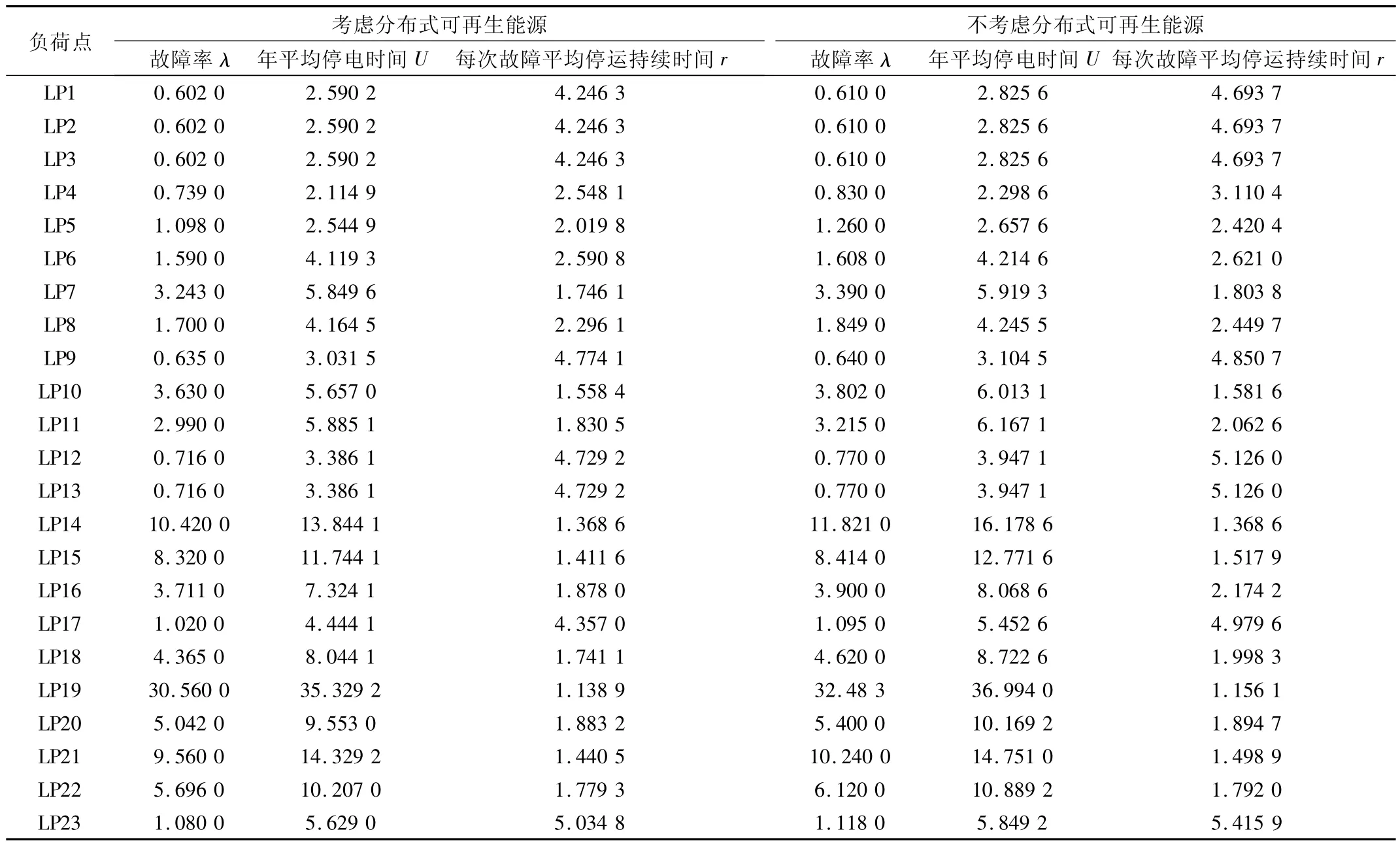
表5 方案1 与方案2 的负荷点可靠性指标对比Tab.5 Comparison of load point reliability indices in scheme 1 and scheme 2

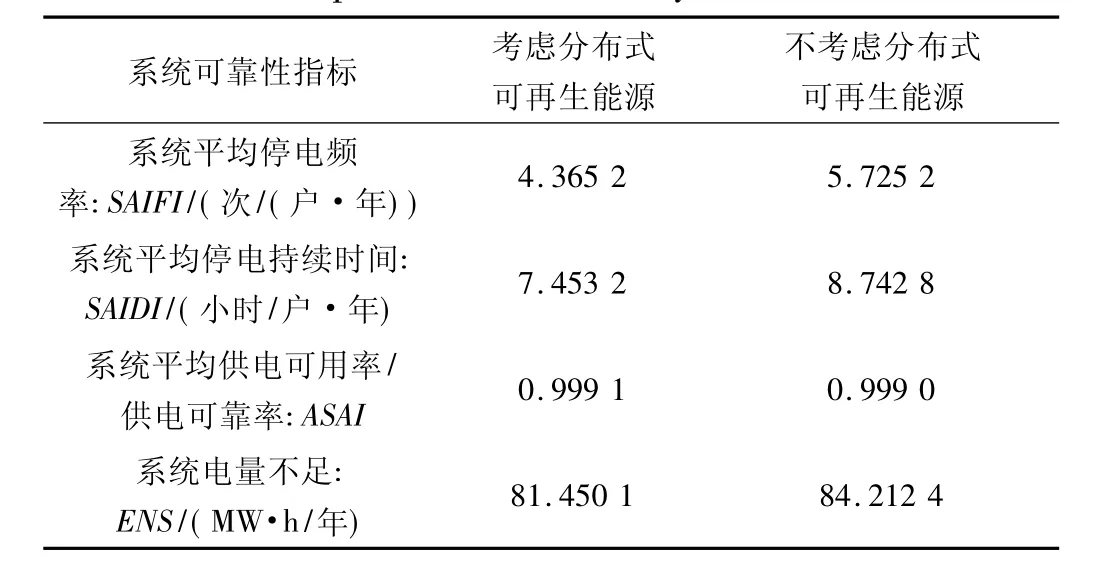
表6 方配电系统可靠性指标对比Tab.6 Comparison of reliability indices of power distribution system

通过对比以上两种场景的可靠性指标，系统平均停电频率SAIFI变化如图14 所示。

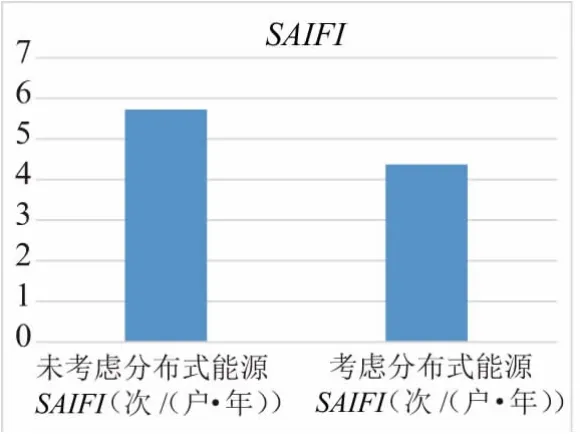
图14 系统平均停电频率SAIFI 变化情况Fig.14 Variation of SAIFI of average power failure frequency of the system

不考虑分布式可再生电源时，SAIFI为5.7252 次/( 户·年) ，考虑分布式可再生电源后，SAIFI变化为4.3652次/( 户·年) ，有效的降低了用户的停电次数，提高配电网的可靠性。

系统的平均停电持续时间SAIDI，在未考虑分布式可再生电源时SAIDI为8.7428 小时/( 户·年) ，考虑分布式电源之后，SAIDI下降到7.4532 小时/( 户·年) ，降低系统的停电时间，提高了配电网的可靠性，如图15 所示。

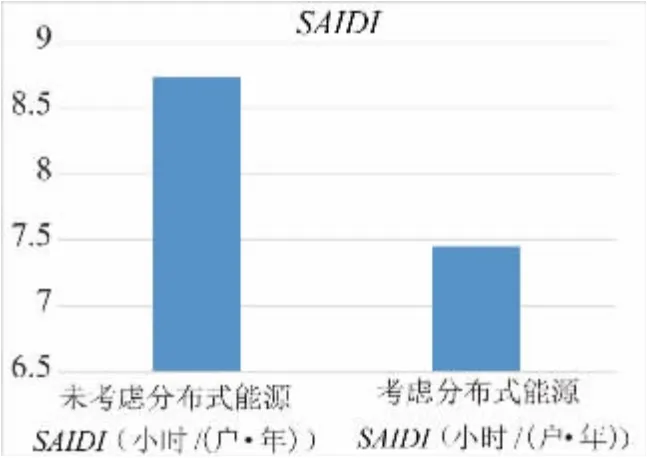
图15 系统的平均停电持续时间变化情况Fig.15 Variation of the average outage duration of the system

在不考虑分布式可再生电源时，系统的平均供电可靠率ASAI为0.9990，在考虑分布式可再生电源之后，系统的平均供电可靠率ASAI上升到0.9991，如图16 所示。

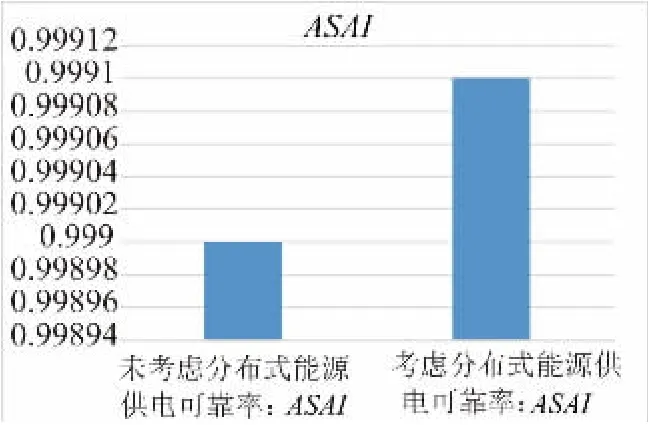
图16 系统的平均供电可靠率变化情况Fig.16 Change of average power supply reliability rate of the system

在不考虑分布式可再生电源时，系统电量不足ENS为84.2124 MW·h/年，考虑分布式可再生电源之后，ENS降低为81.4501 MW·h/年，提高了系统的可靠性，如图17 所示。

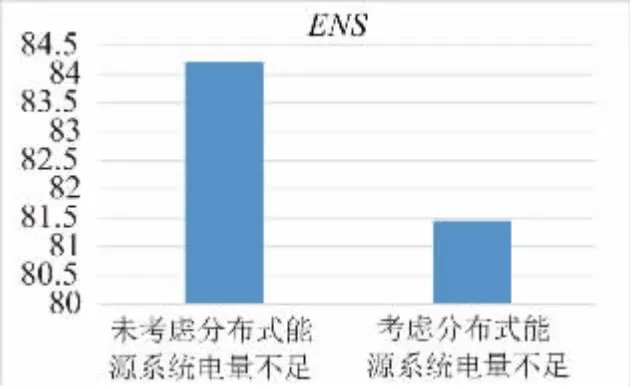
图17 系统电量不足变化情况Fig.17 Change of power shortage of the system

综上所述，在考虑分布式可再生电源之后，系统发生故障时，分布式可再生电源可以形成计划孤岛，可以提高孤岛内负荷点的可靠性，从而整体上改善了系统的可靠性指标，对配电网的可靠性有积极的影响。

6 结束语

文章提出了一种基于序贯蒙特卡罗仿真的考虑孤岛运行和可再生能源不确定性的有源配电网可靠性评估分析法，首先基于两状态马尔科夫模型建立了配电网关键设备和可再生能源场站设备的可靠性模型; 其次，建立了由场站设备状态和可再生能源REPO 概率组成的可再生能源场站通用多状态模型，提出了基于风光资源概率分布函数的风光可再生能源REPO 多状态的划分及其概率计算方法，并进一步提出可再生能源场站5 状态可靠性模型，满足有源配电网可靠性分析要求; 此外，采用馈线分区的概念，划分了孤岛运行的范围，并且根据孤岛内总出力和总负荷之间的关系与负荷权重的大小，进行负荷的削减，提高配电网供电可靠性;最后，通过IEEE RBTS 测试系统分别对考虑和不考虑分布式可再生能源两种场景进行了仿真分析，结果表明，在考虑分布式可再生能源时，所求得的各项可靠性指标都具有明显的提升，提高了配电网的可靠性。同时也验证了所提方法的正确性。