基于分布鲁棒优化的电热综合能源配网系统与氢能源站协同优化

张韶华，王必恒，石城，赵中原

(1.武汉理工大学，武汉 430070; 2.国网宁夏电力有限公司，银川 640000;3.国电南瑞南京控制系统有限公司，南京 211102; 4.南京信息工程大学，南京 210044)

0 引言

近年来，氢能因其高能量密度和无污染，以及在电氢混动汽车等交通领域的潜在应用而受到世界关注［1］。为了降低运输成本，氢气可由氢能源站( Hydrogen Fueling Station，HFS) 现场生产和存储。目前，工业电解的电制氢效率约为70%，耗电量较高［2］。氢能的需求主要发生在白天。为了电力系统的安全运行，HFS通常在午夜或凌晨产生氢气，以避开电力负荷高峰。

在中国西北部，热电联产机组的电力输出取决于热需求。然而，热负荷峰值通常发生在午夜或凌晨，因此，热电联产机组的运行点往往设置在运行区域的边界，降低了热电联产机组的灵活性。此外，对于可再生能源比例较高的电热综合能源配网系统( Integrated Electricity-Heat Energy System，IEDS) 中大量HFS 的安全运行，IEDS 需要更高的灵活性［3-4］。因此，协调运行对于IEDS 和HFS 的经济和安全运行至关重要。然而，HFS 由个人投资和运营，HFS 只与IEDS 共享有限的信息。另一个问题是，整个系统的经济和安全运行对IEDS 中可再生能源的不确定性很敏感。

目前已经针对HFS 的运行调度进行了一些研究。文献［5］提出了多个HFS 的集中式运行优化模型，通过允许过量氢气参与需求响应合同，可以获得额外的收益;文献［6］提出了多个HFS 的分布式双层模型预测控制模型，以在价格不确定的情况下分配能源生产和P2P 交易量的方式使每个HFS 的利润最大化; 文献［7］针对能源市场提出了HFS、新能源电站和电氢混动汽车聚合服务商之间的P2P 储能共享策略，提高了社会福利。然而，这项工作侧重于能源交易网络，而忽略了能源系统的运行约束;文献［8］使用基于纳什议价理论的P2P 交易出清模型来减少HFS 的购电成本，并提高风电的消纳水平。上述研究为降低HFS 的运营成本和提高总利润做出了开创性的工作。然而，除文献［7］外，HFS 被假定仅与电力系统具有能量耦合，而忽略了与其他能源系统如区域供热网络( District Heating Network，DHN) 耦合的潜在影响。

氢能系统中可再生能源的不确定性问题越来越受到人们的关注。为了降低氢能系统的运行成本，文献［9］提出了两阶段鲁棒优化( Robust Optimization，RO)模型。对于该模型，在第一阶段确定了氢能系统的接入位置，在第二阶段将最差风力发电情况下的电氢微网子系统的运营成本降至最低; 文献［10］提出了一种分布鲁棒优化( Distributionally Robust Optimization，DRO) 调度模型，以最小化电力系统和HFS 的运行成本，其中电价的分布受到基于Wasserstein 距离的不确定性集的约束; 文献［11］提出了一种基于Kullback-Leible 散度的DRO 调度模型，用于具有风电不确定性的电力系统和燃气系统的联合运行，其中电力系统和天然气系统通过能源枢纽耦合。然而，这些模型是集中式的，对于具有各种独立实体的能源系统来说忽略了隐私问题。

针对上述问题，文章建立一种IEDS 和HFS 协同的分布鲁棒协同调度模型，并给出分散式协同调度方法。论文的主要创新点: ( 1) 为了经济和安全运行，建立了IEDS 和HFS 的协同调度模型，其中HFS 与热力系统耦合，采用热回收，以降低运行成本并提高热电联产机组的灵活性;(2) 利用数据驱动的不确定集，建立了一个考虑风电不确定性的基于DRO 的协同调度模型，该模型是可分解的并且适用于并行计算;(3) 针对分散式调度，提出了一种改进的Benders 分解( BD) 算法，该算法具有较好的隐私保护和收敛速度。

1 问题建模

1.1 氢能源站运行建模

文中研究的氢能源站的示意图如图1 所示。其中，电能在电解槽( Electrolysis Cell，EC) 中被转化为氢气和热能。氢气储存在氢储能( Hydrogen Storage，HS)中以满足本地氢气需求，或通过燃料电池( Fuel Cell，FC) 转化为电能。

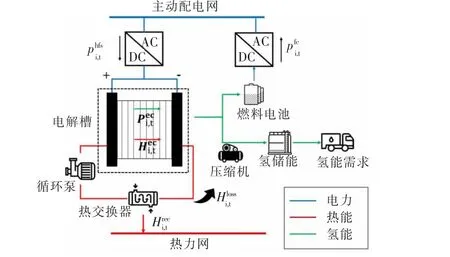
图1 包含P2HH 机制的HFS 示意图Fig.1 Schematic of the HFS with P2HH mechanism

文中假设使用碱性电解槽，利用电转热-氢( Power to Heat and Hydrogen，P2HH) 机制循环利用热能，然后注入DHN 中［3］。IEDS 中有多个HFS，其中第i个HFS的调度问题可以表述为如下的优化问题:

式(1) 为每个HFS 目标函数，其中第一项和第二项分别表示电解槽的运行成本和氢储能中的氢气压缩的成本;T表示调度时长; ρeci和ρhsi分别表示电解槽和氢气压缩的单位成本系数。约束(2) 是基于简化的“T－H－H”可行区域模型，用于计算电解槽输出的氢能和热能，其中a1，i、b1，i、a2，i、b2，i为四个近似参数［9］。约束(3) 描述了电解槽中温度、热损失和循环热功率的热容效应。分别表示热阻、环境温度、热容、热循环效率和电解水产生的热能。约束(4) 为氢储能运行约束，氢储能的气体充入等效功率和气体释放等效功率受压力范围的限制，表示HFS 本地的氢需求、气体常数、氢储能的体积、氢的摩尔质量、燃料电池的效率和氢的低热值。在约束条件中，输入功率燃料电池输出功率、电解槽温度、氢储能充入功率、氢储能释放功率和氢储能压力都是有界的，用带上划线和下划线的符号分别表示相关项的上下值，其简约形式如约束(5) 所示。

1.2 电热综合能源系统运行建模

为清晰表述，第1.2 小节先建立确定风电场景的IEDS 调度模型，考虑风力发电的不确定性的分布鲁棒优化模型将在下节介绍。文中假设IEDS 由主动配电网( ADN) 和DHN 组成，它们由同一公用事业公司管理，并通过热电联产装置耦合。由于风力发电的高渗透性，ADN 采用了智能软开关( SOP) 和静态无功补偿器( SVG) 实现优化潮流和电压分布的分布。采用Dist-Flow 模型［12］表示AND 潮流约束，热网采用恒流变温( CF－VT) 运行模式［13］，建立DHN 的运行约束。确定性IEDS 调度模型如下:

式中上标s、d、S、R 分别为变电站、负荷、供水网和回水网; 下标b 和p 分别为ADN 中的线路和DHN 中的管道;下标pn 和dn 分别为ADN 和DHN 中的母线和热网节点; Ω 为特定设备的集合;［s(i) (e(i) ) ］为支路的结束( 开始) 节点的集合，这些节点是ADN 或DHN 的开始( 结束) 节点。

在目标函数中，第一项和第二项分别描述了网络损耗的成本以及变电站与上游的电力交换。目标函数的最后一项表示CHP 的总运营成本。ρnl和ρex分别表示网络损耗和功率交换的单位成本。变电站注入功率的绝对值形式pst 是用来惩罚逆向潮流。约束描述了CHP 运行成本，其中为凸可行运行区域［14］，Λi和λi是热电联产成本函数的两个系数。基于DistFlow 潮流模型构造约束，其中p、q、P、Q、v、l分别表示注入有功功率、注入无功功率、线路有功功率、线路无功功率、总线电压平方、线路电流平方。约束是SOP 在PQ 控制模式下的工作约束，其中非凸约束可以用分段线性函数［15］来近似。SVG 的无功功率补偿的约束如下所示。约束与采用CF－VT 控制的供水-回水供热管网的DHN有关，其中省略了每个节点的热力站和换热器的内部循环过程。m、T、ψ、c分别表示水的质量流量、温度、传热系数和水的比热容。HFS 回收的热能通过回水网管道注入，可以提高回水网管道的温度，以提供热源［3］。

1.3 氢能源站－电热综合能源系统分布鲁棒调度模型

文章目标是为了找到风力发电最差概率分布下的决策。因此，采用受置信集约束的数据驱动和基于场景的模糊集来覆盖风电出力的任何可能的概率分布［16］。假设存在通过M个历史样本聚类得到的N个离散风电场景。所有N个风电情景的离散概率分布表示为P =[P1，P2，…，PN]。置信集可以用范数L1或范数L∞来定义，如式(15) 、式(16) 所示:

式中Ps，0为根据聚类结果的风电场景s的经验概率;Ps为置信集内风电场景s的概率; α1和α∞是两个常数，代表这两个给定的置信水平。

根据上述公式，基于场景的DRO 调度模型可以表述为如下优化问题:

式中us为风电场景s下调度区间内IEDS 与所有HFS 之间的耦合变量向量;us，i为HFSi的耦合变量;xs和ys，i分别为除耦合变量外的IEDS 和HFSi调度问题中的向量变量;F和Gi分别为IEDS 和HFS 的目标函数向量;fs和gi分别为场景s和HFSi中IEDS 的不等式约束函数。此外，第一个约束对应于式( 9) ～式(13) ，第二个约束对应于式( 2) ～式( 5) ，第三个约束对应式(15) 和式(16) 。此外，考虑风力发电的不确定性，基于式(1) 和式(8) 建立了目标函数。

2 求解方法

2.1 模型分解

由于互斥情景概率，基于场景的DRO 模型独立于风电场景P。因此，在目标函数上的最小化和求和运算可以互换。因而此问题可以重新表述为:

式中φs为场景s中调度问题的最优值，具体形式为:

基于内部场景的最小化调度问题可以并行解决，而外部最大化问题的目标是找出最坏的情景分布。

2.2 基于改进Benders 分解的协同调度算法

在内层问题中，IEDS 和HFS 通过电解槽输入功率和热回收注入功率实现耦合。文中提出了一种改进的基于Benders 分解的算法，以实现一种分散式和可分解的迭代优化框架，得到全局最优解。在求解过程中，IEDS 负责求解ADN 和DHN 的联合调度问题( 即主问题) ，HFS 负责优化了自身运营成本( 即子问题) 。

1)IEDS 主问题:考虑到与HFS 的能量耦合，IEDS 操作员的目标是最小化与ADN 和DHN 对应的运营成本。如第2.2 节中所示的IEDS 的主问题可以重新表述如下:

式中上标(k) 为迭代索引;为由IEDS 对us，i估计的调度结果;为由IEDS 估计的HFSi的运营成本，它受到子问题返回的Benders 割集约束; M，s(k)为主问题的最优值。

2) HFS 的并行子问题:第2.1 节中HFSi的调度问题可重新表述如下:

式中mi、ai、ni、bi、ci是具有相应维数的常系数向量或矩阵。第一个约束是基于HFS 调度模型中的目标函数，而第二个等式约束是由HFSi调度模型中的约束通过添加两个反向松弛转换而来的。

在通过经典的Benders 分解算法接收到来自主问题的能量交换指令后，将在子问题［17］中依次执行可行性检验检查和最优切割生成( 如果有的话) 。在这种情况下，每个HFS 每一次迭代需要解决两个子问题，这是很耗时的，特别是在时间尺度较长的决策调度情况下。论文受文献［18］中松弛变量的启发，将该松弛变量添加到所涉及的约束条件中，以表示主问题和子问题的协同误差。这样就可以将估计成本的可行性纳入可行性检验子问题，并将其转换为一个统一的子问题为:

因此，新的子问题可以被重写为以下紧凑的形式:

因此，在IEDS 操作员将主问题的最优解转移给HFS 后，HFS 管理员只需要解决该子问题一次，并在每次迭代时返回统一的BD 割。所提出的改进的BD 算法可以降低HFS 的计算负担和每次迭代时调度程序的中断次数，总结在表1 中。对于存在多个HFS 的大型IEDS 的情况下，主问题和子问题之间的迭代优化可以采用并行计算加速来进行，而BD 割仅包含对偶变量和耦合变量的值等非隐私信息。

表1 基于改进Benders 分解的协同优化调度Tab.1 Collaborative optimal scheduling based on improved Benders decomposition

3 仿真测试

3.1 测试系统说明

测试系统由改进的IEEE 33 节点ADN 和Barry Island 32 节点DHN 组成，如图2 所示。

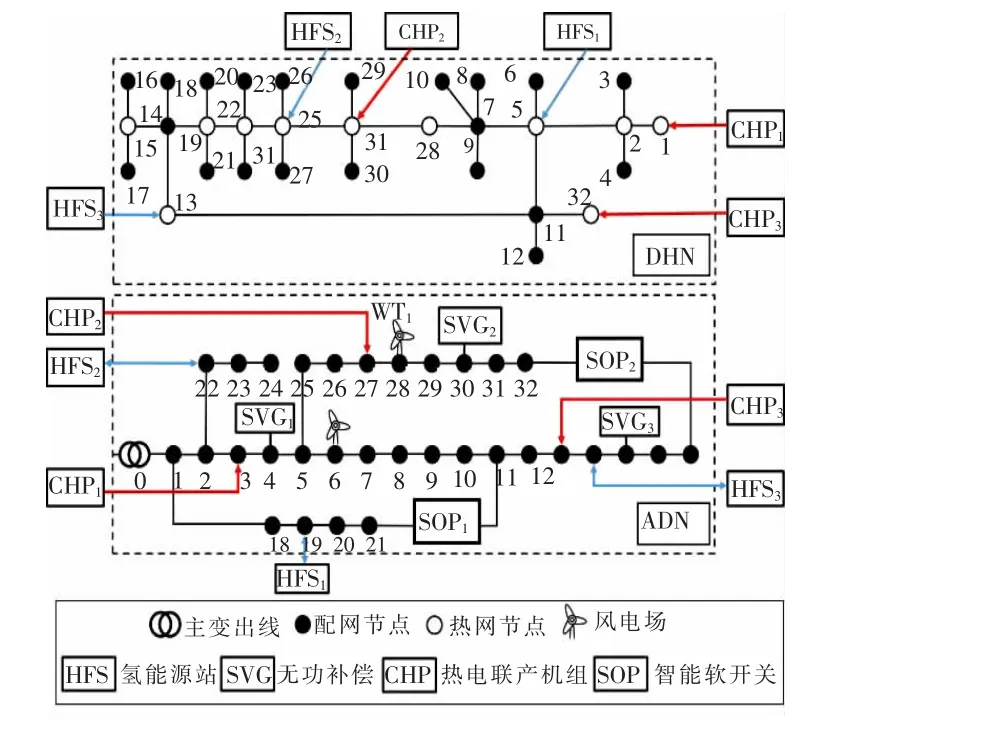
图2 测试系统的拓扑结构图Fig.2 Topology of test system

测试系统中有三个HFS、三个CHP、两个风电场、两个SOP 和三个SVG。测试IEDS 的完整数据可以在［20-21］中找到。两个风电场的容量为1.5 MW。SOP和SVG 的容量分别为1 MV·A 和0.5 Mvar。假设三个CHP 的容量相同为1.5 MW，其成本函数的系数和可行运行区域参考文献［13］。在论文中，三个HFS共享相同的参数，如表2 所示。文章风电数据来源为在线开源数据集文献［22］，并设定目标地点为河北张家口地区，收集2019 年全年风电出力数据。风机模型为Goldwind GW1092500，高度设置为100 m。最后，通过K-means 的时间聚类算法将其聚类为5/10/15/20 种典型风电场景，聚类算法详细步骤可参考文献［23］，这里不再赘述。图3 显示了一天内( 即24 h) 以一小时为时间段的总电负荷、热负荷和氢气需求。环境温度TAt 固定为10 ℃。ρnl和ρex分别设定为0.011 元/( kW·h) 和0.01 元/( kW·h) 。母线电压的变化被限制在［0.95，1.05］p. u. 范围内。仿真采用MATLAB 的YALMIP 工具箱和MOSEK 求解器，在一台3.6 GHz CPU 的个人电脑上进行。修改后的BD 算法的阈值ε 被设定为10－3。

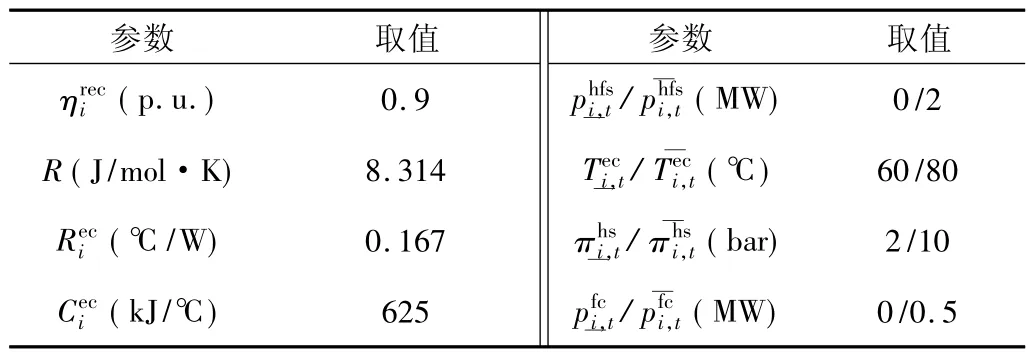
表2 HFS 相关参数Tab.2 Parameters related to HFS

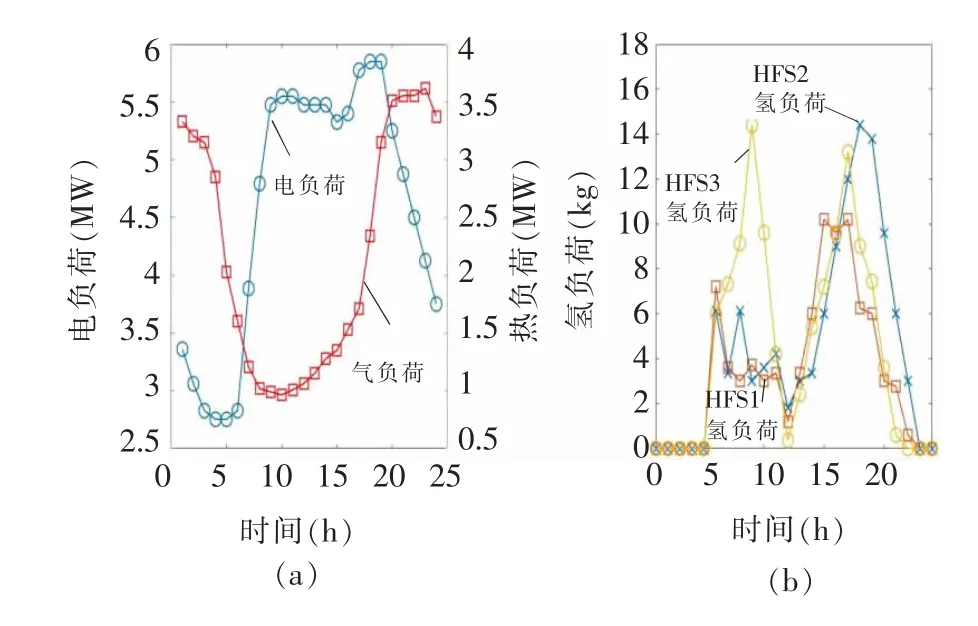
图3 当日电负荷、热负荷和氢气需求Fig.3 Electrical load，heat load and hydrogen demand on that day

3.2 氢能源站－电热综合能源系统协同调度的有效性验证与分析

在某一的风电场景下，研究了测试系统内IEDS 和HFS 的协同调度的有效性和必要性。IEDS 和HFS 的协同调度的最佳运行成本为14.20 ×103$，而仅考虑ADN 和HFS 的调度的最佳运行成本为15.38 ×103$。相比仅考虑与配电网耦合的相关工作［5-8］，文章提出的考虑热网的协同调度运行成本降低了7.8%。图4 显示了热电联产机组在调度范围内的工况点。从图4 中可以看出，在热负荷高峰期，当HFS 中的热量被回收时，CHP1 和CHP2 的热功率输出都有所下降，而当HFS 中没有热量回收时，其运行点达到了功率极限。图4 还显示，运行点从运行区域的边界向内部移动，这提高了CHP 安全运行的灵活性。图5 显示，在1 －7 时刻和20 －24 时刻，当热负荷处于高位时，HFS 制氢过程中的回收热能主要供应给DHN，达到总热负荷的50%。图6显示了测试系统在调度范围内的电量构成。在8－14 时刻和17－19 时刻，电力是通过FC 生产的，作为HFS 对ADN 的电力支持，这意味着风力发电不足以满足电力负荷高峰的需要。图7 和图8 分别显示了在调度范围内HFS 的电力消耗和最佳SOC 状态的曲线。大部分的氢气生产发生在午夜和清晨( 见图7) 。这主要是因为多余的风电应该在低负荷高峰期被HFS 消耗掉，以达到调度范围内的安全水平，如图8 所示。

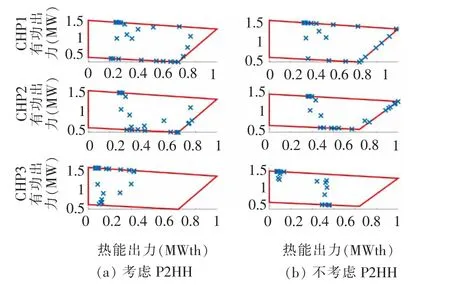
图4 热电联产机组全天的工况点情况Fig.4 Operating points of the CHP units on that day

图5 系统全天热能供应来源的构成Fig.5 Composition of heat supply source on that day

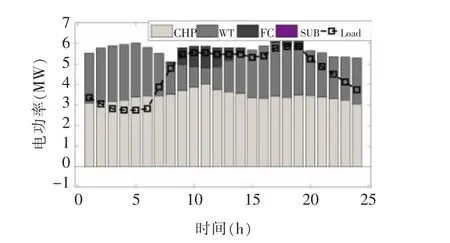
图6 系统全天发电量来源构成Fig.6 Composition of power generation on that day

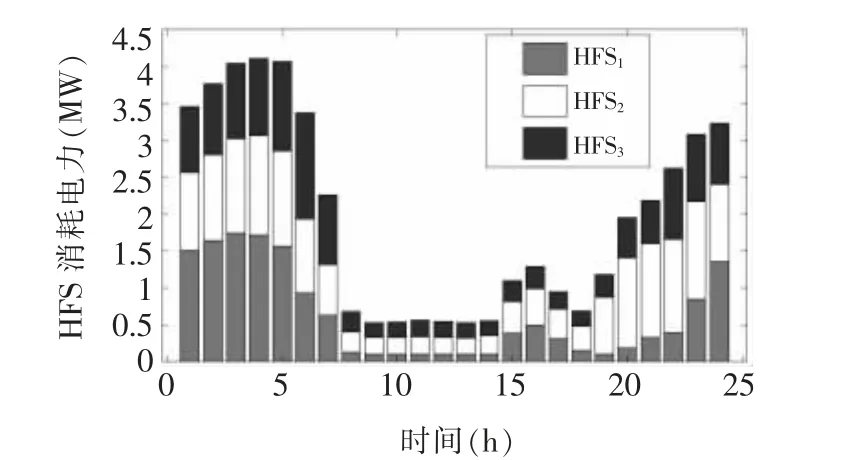
图7 HFS 全天耗电量情况Fig.7 Power consumption of HFSs on that day

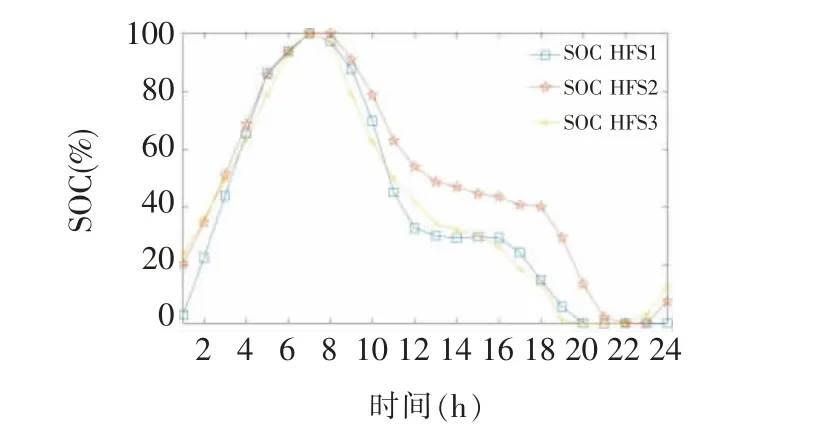
图8 HFS 全天氢储能SOC 状态Fig.8 SOC states of HFSs on that day

3.3 DRO 协同调度应对风电不确定性的优势对比验证与分析

为了验证使用所提出的DRO 协同调度模型处理风电不确定性的有效性，文章总结了不同置信度和范数约束下的最优解，并与另外两种出力风电不确定性的优化模型进行对比，如表3 所示。其中，风电数据被聚类为20 种典型场景。用于对比的模型包括使用蒙特卡洛方法的随机优化( Stochastic Optimization，SO)模型，其1000 个随机场景由使用上述收集的风电数据的ARIMA 模型生成，以及根据每个时隙收集的数据的最大值和最小值的带有盒式不确定集的RO 模型。如表3 所示，随着置信度的提高，最优运行成本更接近于使用RO 模型，否则，最优运行成本将倾向于使用SO模型得到的结果。

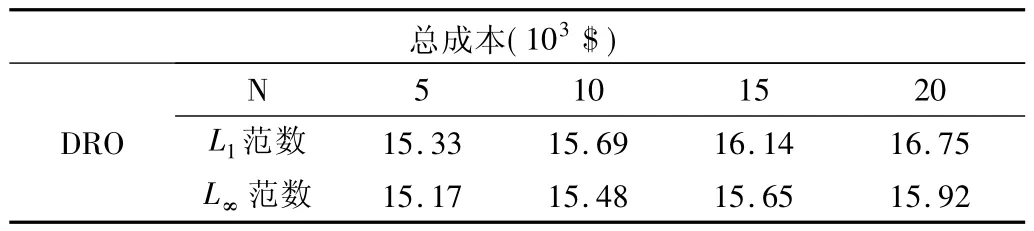
表3 不同场景样本数下的DRO 调度结果Tab.3 DRO dispatching result of under different clustering scenarios with different number of samples

表3 所示的最优解也意味着置信度α1( α∞) 对范数L1得到的最优解的影响比范数使用L∞得到的最优解的影响小。论文还研究了不同风电场景聚类数量下的调度结果，结果汇总于表4。文章按文献［24］中的设置，置信度被设定为0.95。

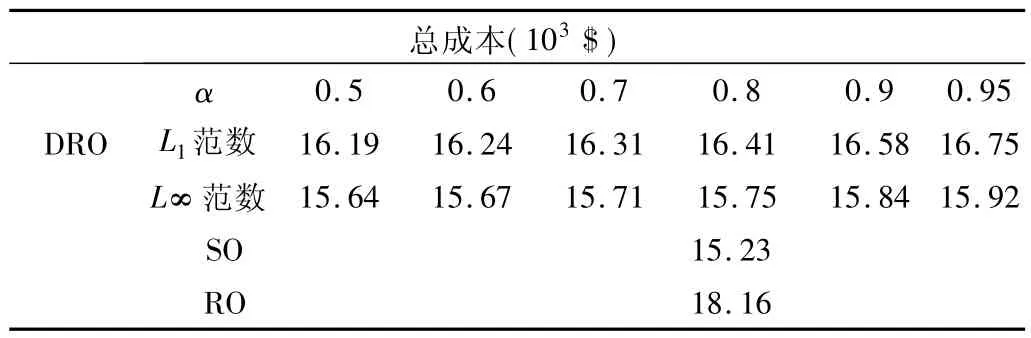
表4 SO 和RO 的性能比较Tab.4 Performance comparison with SO and RO

从表4 可以看出，场景数越大使得最优解越接近于使用RO 模型得到的最优解，相反，场景数越小越接近于使用SO 模型得到的最优解。因此，置信度和风电场景聚类的数量可以被认为是权衡使用SO 和RO 模型的最优解的预算参数。

3.4 改进BD 算法有效性对比分析验证

表5 中总结了不同算法性能比较。可以看出，使用改进BD 算法和经典BD 算法的解决方案都收敛到了最优解。为了获得协同调度问题的最优解，与经典BD 相比，论文方法只需要大约一半的迭代次数，求解时间缩短了约70%。因此，使用改进BD 算法进行日前调度的总CPU 时间是可以接受的，并且可以通过并行计算技术进一步减少。图9 显示了改进BD 算法的迭代过程，可以看出，该算法在大约692 次迭代中收敛到了最优解。

表5 计算性能Tab.5 Computational performance

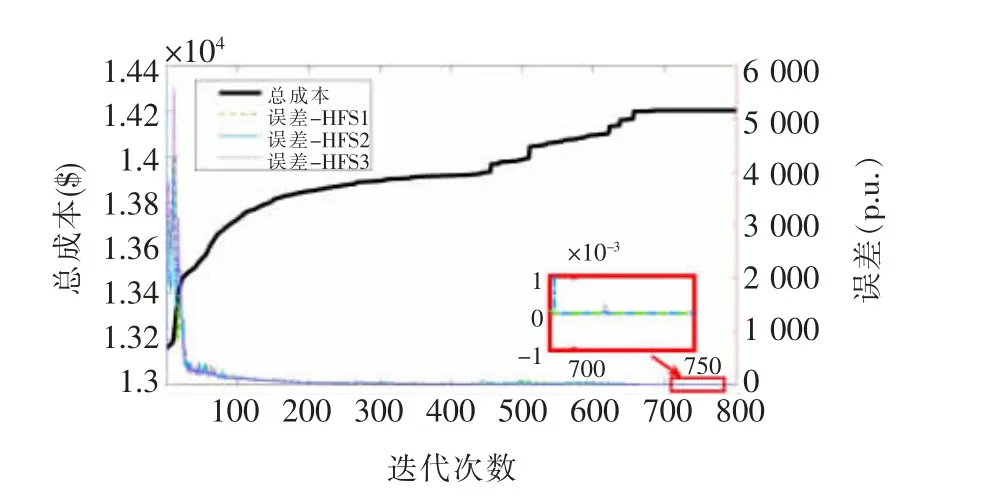
图9 改进BD 算法求解的迭代过程Fig.9 Iteration process of the modified BD algorithm

4 结束语

文中提出了一种用于IEDS 和HFS 运行的分布鲁棒协同调度模型，其中HFS 中产生的热能被回收并注入热力系统，以降低运行成本实现安全运行。该模型采用改进的BD 算法以并行方式进行分解和求解，用于IEDS 和HFS 之间的分散式调度并实现隐私保护。在仿真模拟中，文中给出并分析了IEDS 和HFS 协同调度的优势，应对风力发电不确定性状态的有效性，以及使用改进型BD 算法的良好计算性能。未来的工作将侧重于研究分配协同调度所获利润的策略。