基于系统寿命分布的智能电能表时钟电池欠压预测研究
朱毓,金耀,陶琳,鲍震峰,龚国庆,周尧
( 国网安徽省电力有限公司营销服务中心,合肥 230088)
0 引言
智能电能表是智能电网的重要组成部分[1-2],在贸易结算与管理、用电信息采集、智能用电等方面发挥着重要作用[3]。时钟电池是智能电能表关键器件,若其故障或欠压会导致电能表显示时间复位与时钟紊乱。在推进电力市场现货交易的背景下,会导致费率切换出错,冻结电量转存错误严重问题[4]。国网某省公司2018 年5 月至2019 年10 月现场拆回电能表分拣结果显示,拆回故障表计979196 台,其中因时钟电池欠压拆回的表计达到779139 只,占比79.5%。电池欠压故障在智能电能表现场运行过程中具有普遍性。我国智能电能表挂网数量超过6 亿台,分布地域广,准确研判并预计时钟欠压对保证智能电能表可靠稳定运行和科学制定运维规划具有现实意义。
智能电能表电池欠压主要从欠压对电能表的影响、欠压触发原因、电池寿命三个方面展开研究[5]。在欠压影响方面,文献[6]梳理出电池欠压会引起主站抄读数据错误、电能表报警灯常亮和背光常亮、电表液晶屏显示ERR-04 或ERR-08、电能表液晶屏显示内容固定在一屏、以及电能表进线侧停电时液晶屏黑屏5种故障模式;文献[7]进一步分析电池欠压时频繁掉电对智能电能表计量性能的影响;文献[8]研究了电池欠压对表计误差、表计计时、计费、远程费控、冻结数据5个性能指标的影响,并从硬件、软件、电网选型等多角度提出了电池欠压故障解决方案; 文献[9-10]从电池质量、电池钝化、外围电路漏电、外围器件损伤、软件设计缺陷5 个方面分析了电池欠压触发诱因,提出了减少欠压故障的措施和针对电池欠压的状态监测方案。针对时钟电池寿命,文献[11]通过测量不同放电深度脉冲电压的变化值,通过数据模拟,建立了脉冲电压与剩余电量的数学模型,预测ER 14250 电池剩余电量。文献[12]设计了不同环境温度下智能电能表电池耗电回路的电流试验,利用Adaboost 算法改进BP 神经网络预测模型,建立智能电能表内置电池容量预测模型;文献[13]采用加速测试及半经验方法的建立电池的寿命预测模型。上述研究表明,现有时钟电池欠压量化分析仅能从电池自身失效或退化开展寿命评估与预测,虽然诸多研究成果显示触发时钟电池欠压的若干原因有多种,但如何将多种触发原因纳入到时钟电池欠压量化评估尚缺少有效方法,目前研究尚处于空白.
时钟电池欠压属于可靠性范畴,其触发原因涉及多种类型器件,器件可靠性数据类型具有多样性,如何融合多样可靠性信息开展时钟电池可靠性评估是系统可靠性综合领域的一个难点与热点。从数据基础层面,侧重于利用单元寿命数据、成败型数据、经验数据[14-15]。如文献[16]利用单元成败型数据和Weibull 型数据开展系统可靠性评估。从可靠性测度概率估计结果层面,侧重于给出可靠性测度置信限。通过计算二项、指数型单元组成的串联系统寿命分布,可给出系统可靠性测度精确置信限[17]。若单元寿命分布具有多样性的条件下,则难以计算系统寿命分布,仅能给出系统可靠性测度的近似置信限[18-19]。借助现代计算机技术,利用通用生成函数、P-value 函数、Copula 函数仅可计算系统可靠性点估计,因为不能求解系统寿命分布,尚难以给出置信限估计[20-21]。如何利用单元可靠性信息求解系统寿命分布是该领域研究的难点。
智能电能表组成器件通常批量采购获得,器件可靠性信息由供应商提供,且可靠性信息具有多样性,如寿命型数据、退化型数据、失效分布、或产品手册提供的失效率信息等。因此,如何融合多样性单元可靠性信息求解系统寿命分布,进而预测系统寿命是时钟电池寿命预测的难点。
文中从时钟电池回路出发,从系统层面分析引起时钟欠压的诱发原因,并将多种诱发原因融合到时钟电池寿命预测,提出一种基于系统可靠性综合的时钟电池欠压预测方法,技术路线结构框图如图1 所示,为电能表可靠稳定运行和运维规划制定提供一种新思路。

图1 基于系统可靠性综合的时钟电池欠压预测方法技术路线结构框图Fig.1 Technical route structure block diagram of clock battery undervoltage prediction method based on system reliability synthesis
1 时钟电池回路系统可靠性模型
时钟电池回路如图2 所示。由电源芯片转换得出的主电源电压大于电池电压,二极管D1未导通,电能表内部器件由主电源供电,电池通过放电回路进行较小电流放电,单片机接收电压检测信号实时检测电池电压V1。电路中保护电阻R3的作用是防止二极管失效时主电源对电池快速大电流充电造成危险,起到保护电池的作用。
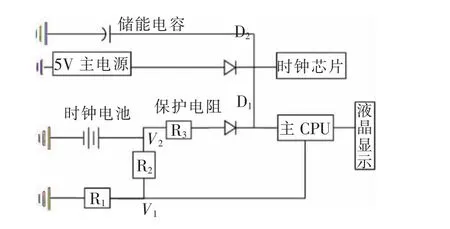
图2 电源回路Fig.2 Power supply circuit
当电能表掉电,进入低功耗工作模式时,转由时钟电池给单片机、停电LCD 显示、时钟芯片供电。此时,若单片机模块没有进入低功耗工作模式,则需要毫安级电流供电,时钟电池很快电量耗尽。若电阻R2和R1短路失效,则时钟电池短路,电量快速耗尽。若二极管D1和保护电阻R3开路,使得时钟丧失电池供电。此外,若电池本身存在质量缺陷,也很快就耗尽电量而失效。据此可知,电池失效、R1和R2同时失效、二极管D1开路、保护电阻R3开路、单片机模块没有进入低功耗工作模式4 种情况中任一情况出现,都会触发电池欠压。
针对电池欠压失效模式,时钟电池回路系统可靠性逻辑关系如图3 所示。
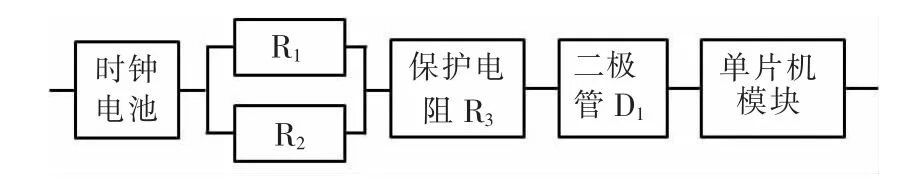
图3 时钟电池回路系统可靠性逻辑框图Fig.3 Clock battery circuit system reliability logic block diagram
构建系统可靠性模型:
式中RS为系统可靠度函数;R电池、RR1//R2、RD1、R3、R单片机分别为电池可靠度函数、R1与R2并联子系统可靠度函数、二极管D1可靠度、保护电阻R3可靠度、单片机模块可靠度函数。
智能电能表时钟电池欠压诱发原因包括电池质量、外围器件损伤、软件设计缺陷、外围电路漏电造成的。软件设计集成于单片机,可与单片机模块集成在一起考虑。因此,评估电能表时钟电池欠压需要综合考虑包括电池在内的时钟电池回路可靠性。
不同型号智能电能表时钟电池回路可能有差异,电源工作模式也有区别,但本部分所提供的系统可靠性建模方法同样适用。只需明确时钟电池回路结构,功能与工作流程,就可阐释清楚组成单元与时钟电池回路系统的可靠性逻辑关系,据此可构建时钟电池回路系统可靠性模型。因此,时钟电池回路系统可靠性建模方法具有普适性。
2 时钟电池回路系统寿命分布
电能表组成元器件由供应商配套,可通过供应商获得各单元的可靠性数据。其次,作为具有长时间运行历史的量测设备,具有一定历史累积数据,可从中提炼出器件的可靠性数据信息。各组成单元可靠性信息具有多源性、多样性,给时钟回路系统可靠性综合带来困难。
2.1 退化型单元寿命分布
性能数据是器件可靠性数据的一种重要形式,如时钟电池放电记录体现了电池容量、电池端电压不断降低至失效的过程,若将该过程视作电压指标的退化过程,则可利用Wiener 过程描述时钟电池电压衰减过程,在获得电压失效阈值的基础上,就可确定时钟电池寿命分布。若t时刻电池电压衰减记为X(t) ,那么{X(t) ;t}服从Wiener 过程:
式中W0(t) 为标准的Wiener 过程;a是漂移参数;σw是扩散参数。当电能表时钟电池电压X(t) 衰减到给定阈值ε 时电池失效,电池寿命定义为:
式中X(t) 服从Wiener 过程,则首次达到阀值时的时间分布为逆高斯分布,其概率密度函数为:
在获得电池电压衰减数据(X(ti) ,ti) 后(i= 1,2,3,…,n) ,可得到电池电压衰减量的条件概率密度函数,假设各电池样本相互独立,则可构建似然函数,并进一步获取对数似然函数,而后分别对参数a,σw求偏微分,则待估参数的极大似然估计值为[22]:
式中n个时间区间的增量为( Δt0,ΔX0) ,…( Δti,ΔXi) ,…( Δtn,ΔXn) ,其中ΔXi=Xi-Xi-1,ΔXi为时钟电池在时刻ti和ti-1区间内的电压衰减量,Δti=ti-ti-1,Δti,为时刻ti和ti-1的时间间隔。
2.2 寿命型单元寿命分布
产品常用寿命分布有指数分布、Weibull 分布、正态分布,其概率密度函数为:
式中λ 为指数分布参数;β 和η 为Weibull 分布参数;μ 和σ 为正态分布参数。获得单元的故障时间数据( τ1,τ2,…,τj,…,τm;m= 1,2,…) ,则可利用产品统计推断方法计算单元寿命分布参数[18]。
2.3 依据预计标准确定电子器件寿命分布
电阻作为典型的电子器件,R1、R2、R3、D1寿命可认为服从指数分布,其分布参数失效率λR1,λR2,λR3,λD1。可通过查找Datasheet 获得性能与环境适应性参数,结合IEC 62059,IEC 62380,GJB 299 或者SN 29500等可靠性预计标准,确定器件失效率。即R1、R2、R3、D1的寿命分布为fR1(t;λR1) 和fR2(t;λR2) ,fR3(t;λR2) ,fD1(t;λD1) 。
依据IEC 62380 标准,确定电阻和二极管失效率。电阻失效率预计模型为:
对于固体低损耗薄膜电阻,πType-I=0.1,πType-II=1.4 ×10-3。对于固体低损耗表面贴装电阻,πType-I=0.01,πType-II=3.3 ×10-3。( πt)i为第i个任务阶段的温度影响因子,πt=,电阻温度tR= tA+85×,tA为环境温度。τi为第i个阶段任务剖面的结温下,器件工作时间比率,按年比率计算τi=。y为划分的任务阶段数,即i=1,2,…,y。τon为器件的总工作时间比例,,τoff为器件在存储或休眠模式下的时间比例,τoff=1 -τon。( πn)i为热循环次数影响因子,它与第i个阶段内年累计热循环次数有关,当年累计温变周期次数ni≤8760 周期/年,,若ni>,( πn)i=1.7 ×。ΔTi为第i个任务阶段内的温度(tae) 的平均变化。πN为电阻网络中电阻数量,对于固体低损耗薄膜电阻πN=1,对于固体低损耗表面贴装电阻,。
二极管失效率预计模型为:
式中πU为使用频率修正因子; λ0为二极管基础失效率;τi为第i个阶段任务剖面的结温下二极管工作时间比率;λB为二极管封装的基础失效率;πI为二极管用作接口时的功能类型修正因子;λEOS为由过电应力引起的失效率,作为保护接口使用时,通常πI=1,λEOS=40 Fit,( πt)i为第i个任务阶段的温度影响因子,它与第i个任务阶段二极管的结温有关,(0.4electron - volt) ,式中tj为器件结温。
2.4 基于时变权重的时钟电池回路系统寿命分布
时钟电池回路系统是典型的串并联系统,其可靠度函数模型如式( 1) 所示。根据可靠度函数与概率密度函数的内在关系,可计算系统寿命分布:
式中CBat(t) 、CCPU(t) 、CR1(t) 、CR2(t) 、CR3(t)和CD1(t) 是时钟电池权重、单片机模块权重、电阻R1权重、电阻R2权重、电阻R3权重和、二极管D1权重,考虑时钟回路系统中各元器件可靠性的差异性,且各元器件可靠性随时间演变的过程,单一的主观赋权方法或恒定赋权方法存在人为因素干扰和整体偏差的局限性。因此,本文提出一种时变权重方法,该方法基于时钟电池回路系统可靠性逻辑模型更新权重,则时钟电池权重、单片机模块权重、电阻R1权重、电阻R2权重、电阻R3权重和二极管D1权重分别为:
式中R(·) 为可靠度函数;F(·) 为不可靠度函数。
2.5 智能电能表电池欠压预测
在获取系统寿命分布密度函数式(12) 基础上,根据可靠性各特征量之间的关系,可得时钟电池回路系统寿命的一阶矩和二阶矩阵为:
在给定时刻t,触发电池欠压时间的概率为:
3 实验验证与分析
某型号电能表时钟电池回路由锂亚电池、单片机模块、电阻R1、电阻R2、电阻R3、二极管D1组成。各组成单元可靠性信息如下。
对8 只额定电压3.68 V 的国产ER 14250 型锂亚电池在室温下进行电池容量试验。将8 块电池与电阻连接为通路置于室内,室内温度为23 ±2 ℃,进行恒电阻放电,负载电阻为7.5 kΩ,精度1%,最大功率1/4 W,直接测量电池负载两端工作电压,全部试验样本的电池负载截止电压为2.8 V。在试验中为加快放电速度,负载电流490 μA,而实际时钟电池工作模式下电流大致为10 μA,试验放电电流相比实际放大了49 倍,可认为试验放电一天相当于工作模式下放电49 天。等比例放大49 倍后电池放电数据如图4 所示。

图4 锂亚电池放电数据Fig.4 Lithium sub-battery discharge data
通过模型计算电池寿命分布时采用上述换算方式计算模型参数。第2.1 节中退化型单元寿命分布模型,利用试验中的电池电压衰减数据,通过式(5) 和式(6) 得出:a=0.000369896,σ2W=0.000140475,取ε=2.8,根据式(4)得到锂亚电池寿命分布概率密度函数如式(22) 所示,式中时间t单位为天,图5 为其概率密度函数图形。

图5 时钟电池低功耗模式工作寿命分布Fig.5 Distribution of working life in clock battery standby mode
电阻R1、R2、二极管D1寿命可认为服从指数分布,其分布参数失效率λR1,λR2,λD1通过查找Datasheet 得到:λR1=12Fit =1.2 ×10-8h-1,λR2=20Fit =2 ×10-8h-1,λR3=16Fit=1.6 ×10-8h-1,λD1=8Fit=0.8 ×10-8h-1。根据式(7) 得到R1和R2的寿命分布概率密度函数fR1(t) 、fR2(t) 、fR3(t) 、fD1(t) 如式(23) ~式( 26) ,式中时间t,单位为小时,图6 为其概率密度函数图形。
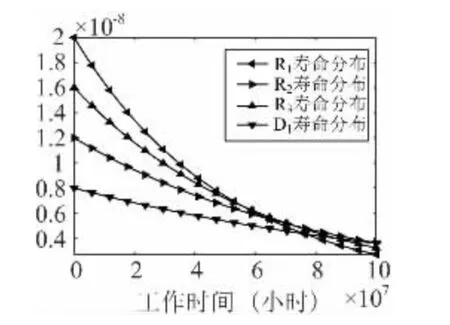
图6 R1、R2、R3、D1寿命分布Fig.6 Life distribution of R1,R2,R3 and D1
通过现场拆回故障数据提取单片机模块故障数据,选择Weibull 分布拟合单片机模块寿命分布,Weibull 分布参数β=1.1566;η=52.6 年。根据式(8) 得到单片机的寿命分布概率密度函数fcpu(t) 如式(27) ,式中时间t,单位为年,图7 为其概率密度函数图形。
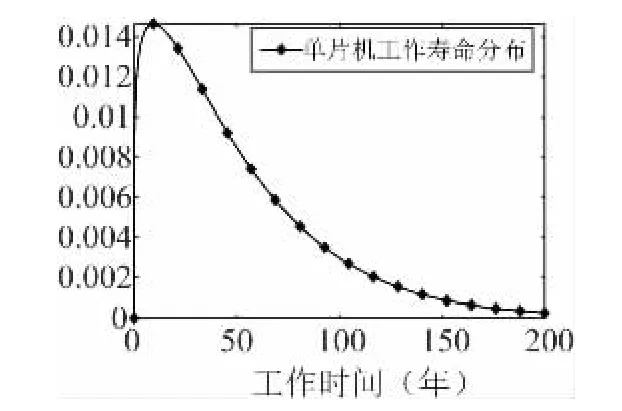
图7 单片机工作寿命分布Fig.7 Microcontroller working life distribution
根据系统可靠性模型可得出系统可靠度Rs及回路系统发生欠压事件概率Fs(t) 与工作时间的关系如式(28) ,根据式(12) 得到回路系统寿命分布概率密度函数fs(t) 如图8 所示。
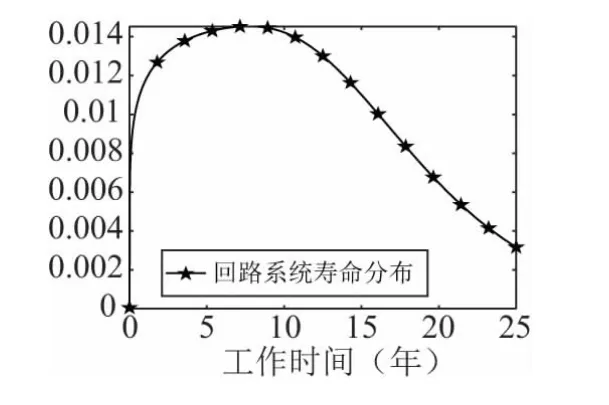
图8 时钟电池回路系统寿命分布Fig.8 Clock battery loop system life distribution
回路各部分及系统可靠度与工作时间关系如图9所示。
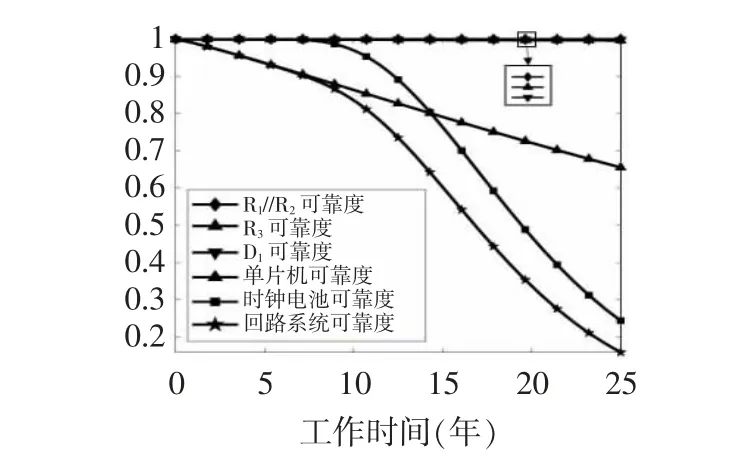
图9 回路各部分及系统可靠度Fig.9 Circuit parts and system reliability
计算时钟电池回路系统平均寿命、可靠度为0.6、0.7、0.8、0.9、0.95 时的可靠寿命如表1 所示。

表1 时钟电池回路寿命预测结果Tab.1 Prediction results of clock battery loop life
给定时间t为4 年、5 年、6 年、8 年、10 年时,回路中电阻R1//R2可靠度RR1//R2、单片机工作可靠度Rcpu、时钟电池可靠度RBat、保护电阻R3可靠度、二极管D1可靠度,系统可靠度Rs与电能表触发电池欠压事件的概率Fs如表2 所示。
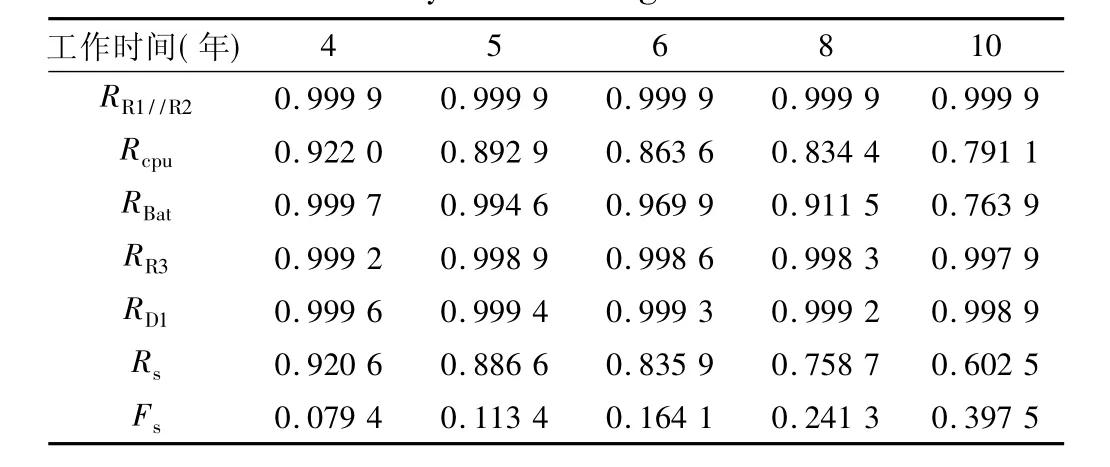
表2 电能表触发电池欠压事件的概率Tab.2 Probability that the electricity meter triggers a battery undervoltage event
以国网某省电力公司2018 年5 月1 号~2019 年10 月14 号拆回分拣4131737 只电能表为数据基础,分析可知其故障表数量979196 只,且按照电能表运行时间统计,现场电能表时钟欠压的故障数据如表3所示。

表3 现场电能表时钟欠压故障数据Tab.3 Electricity meter clock undervoltage fault data on site
将表1 与表2 的预测结果与表3 对比分析发现,时钟电池回路寿命预测结果与现场结果基本一致,体现了文中方法的有效性。
4 结束语
文中针对电能表电池欠压失效模式构建了时钟电池回路系统可靠性模型,提出了一种基于系统可靠性综合的时钟电池欠压预测方法。该方法综合考虑了时钟电池自身以及外围电路对时钟欠压的影响,并创建了预测模型,解决了智能电能表电池欠压事件不能量化评估与预测的问题,有助于科学安排电能表轮换维修等运维规划。此外,结合电能表器件可靠性数据来源具有多样性给统计分析带来困难的问题,文中方法综合利用了时钟电池回路组成单元故障数据、性能退化数据、以及寿命分布信息,创新性地提出时变权重以构建时钟电池回路系统寿命分布,实现了基于系统可靠性综合的时钟电池欠压预测,解决了时钟欠压预测方法工程适用性问题。研究成果可为电池欠压提供一种量化预测技术途径,有助于优化设计减少电池欠压故障的发生,为推进电力市场现货交易建设提供支撑,对智能电网运行稳定性与可靠性也有现实意义。

