区域综合能源系统供需双侧多能博弈互动策略

范宏，袁宏道

( 上海电力大学电气工程学院，上海 200090)

0 引言

随着国家能源市场改革的不断深化，电、气、热等能源已经由垄断逐步走向市场化，由于综合能源市场参与主体众多，因此建立合理的能源交易机制，在保证各市场参与主体安全运行的前提上寻求利益均衡的能源交易优化策略，对推动能源市场的发展具有重要的意义［1］。

区域综合能源系统( Region Integrated Energy System，RIES) 起到“承上启下”的作用，是大电网与用户之间的纽带，能够满足区域内用户的多种用能需求［2］。当前，国内外学者对于RIES 的协同优化和能源市场交易层面已展开了研究。

文献［3］将电转气装置进行精细化建模，计及源荷双侧的不确定性建立两阶段鲁棒模型，寻找可再生能源出力以及负荷最恶劣场景进行优化调节。文献［4］建立了计及可转移负荷的电-气互联系统的多目标优化模型，利用模糊集方法和加权综合指标法进行优化求解。文献［5-7］提出了能源市场参与的RIES 优化调度，但是RIES 仅作为能源价格接受者，没有充分考虑与上级能源经销商以及用户之间的互动，只是通过内部各能源耦合设备的出力来进行优化调节。

随着综合能源市场化的推进，RIES 中各能源主体的交互不断深入，能源价格会影响用户用能需求，用户用能需求也会反作用于能源价格［8］，针对这一利益冲突，现有学者采用博弈论等方法进行研究。文献［9］考虑风电和负荷的不确定性，基于非合作博弈理论建立了电、气网公司净收益模型，力求在不确定因素下保证各能源公司的收益最高。文献［10］建立了一主多从的综合能源系统博弈互动模型，将综合能源销售商为领导者，冷热电联供运营者和用户作为跟随者，来追求各能源主体利益最大时的交易策略。文献［11］重点考虑用户需求侧的能源响应，基于演化博弈理论，分析不同用能方式对于电-气互联系统的影响。文献［12］基于重复博弈理论将微能源网和配电网作为博弈对象，以配电网内电容器的投切来改变对微能源网的供电响应，通过自适应粒子群算法得到两者的博弈均衡结果。文献［13］建立了包含产能基地、系统管理商和用户的供需双侧博弈模型，提出了一种两阶段博弈策略，通过电价型和激励性综合需求响应实现供需双侧联合优化。上述文献虽然已经提出了多能源主体博弈互动框架，但是大多基于电能作为博弈互动对象，未充分考虑电、气、热等负荷及其能源价格对博弈结果的影响，且现有研究大多仅基于能源枢纽与用户之间的互动交易，也未考虑能源枢纽中储能设备对于能源交易的影响。

本文考虑电、气、热负荷及其能源价格，建立能源枢纽供需双侧的多能博弈互动模型。在供给侧，能源枢纽以自身收益最高来决策能源购买量，能源经销商通过调整售能价格来刺激能源枢纽的购能量; 在需求侧，能源枢纽通过调整给用户的售能价格以及各能源转换设备出力使得自身收益最高，而用户通过调节负荷大小来响应售能价格以达到用能成本最小。通过分析证明了所提博弈互动模型存在唯一的纳什均衡解，并采用粒子群优化算法求解。通过算例结果证明了能源枢纽供需双侧的多能博弈互动框架下，RIES 能够实现优化运行的目标。

1 RIES 博弈互动框架

文章构建的RIES 如图1 所示，涉及电、气和热三种能源形式，包含风力发电、能源转换设备以及能源储存设备。RIES 包括了能源经销商( Energy Dealer，ED) 、能源枢纽( Energy Hub，EH) 以及用户( Energy User，EU) 三个能源主体。EH 中主要包括风力发电机、热电联产设备( CHP) 、燃气锅炉( GB) 、电锅炉( EB) 、电转气设备( PtG) 以及储电设备( SE) 。

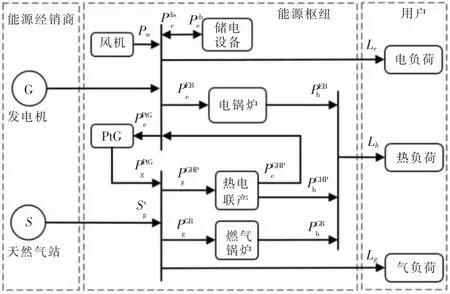
图1 RIES 结构图Fig.1 Structure diagram of RIES

RIES 博弈互动架构如图2 所示，参与博弈的有能源经销商、能源枢纽和用户，能源枢纽作为多种能源转换传输的纽带，在接收到能源经销商的售能报价之后，通过调整购能量和各能源转换设备的出力来使得自身收益最大化，还可以通过制定销售给用户的能源价格来改变用户的用能习惯。能源经销商通过能源枢纽的购能量来调整销售策略，使得自身利益最大化。用户则通过改变用能负荷大小来适应能源枢纽的售能价格，满足自身的用能效益。

图2 RIES 博弈互动架构图Fig.2 Game interaction framework of RIES

2 各能源主体决策模型

2.1 能源经销商模型

能源经销商考虑售能侧出力计划与用户侧用能需求，并制定能源价格，目标是能源经销商的利益最大化，目标函数可表示为:

式中FED为能源经销商的利润;T为总时段数，文中为24 个小时;为t时段能源经销商售能收入;和分别为能源经销商发电机和天然气站的运行费用。

式中Δt为时间长度;和分别为t时段能源经销商发电机组和天然气站的出售功率;和分别为t时段能源经销商的售电价格和售气价格;ae、be、ce和ag、bg、cg分别为能源经销商发电机和天然气站的运行费用系数。

2.2 能源枢纽模型

能源枢纽在确定能源经销商电价以及天然气价格的情况下，调整向用户的售能价格以及内部各个能源转换设备的出力，优化目标为能源枢纽销售收益与运行成本之差最大，目标函数为:

式中FEH为能源枢纽的收益;为t时段能源枢纽售能收入;comc为各能源转换设备运行维护费用;cpec为能源枢纽污染排放费用。

式中λe、λg、λh分别为能源枢纽向用户的售电、售气、售热价格;Le，t、Lg，t和Lh，t分别为t时段用户电、气和热负荷功率实际值;k表示各能源转换设备编号;为k类设备运行维护费用系数;为k类设备t时段出力; ρ 为单位污染排放费用系数;Pw，t分别为t时段风电出力实际值。

2.3 用户模型

多能博弈互动过程中，用户侧在确定电、气、热价格后，用户响应价格调整自身用能需求，还要同时考虑用户的用能满意程度，其模型为:

式中FEU为用户用能成本;fEUt 为用户的用能依赖成本函数，可表示为下式( 12) 各类能源的二次函数表达式，是指用户对于m类能源m∈ {e，h，g} 的需求程度的量化。用户对m类能源的依赖程度越高，则fEUt越大，说明用户愿意承受更高的用能成本来满足用能需求。

式中γm为用户对m类能源的需求程度，表示用户对于该类能源的依赖程度，其值越大，说明用户对于该类能源的需求越高，进而影响用户对该类能源的需求量大小;Dm，t为用户m类能源负荷的初始大小。

2.4 约束条件

RIES 系统需满足各类能源供需平衡约束、能源转换设备运行约束、能源储存设备运行约束以及能源交易约束。

2.4.1 能源供需平衡约束

2.4.2 能源转换设备运行约束

1) CHP 运行约束。

2) GB 运行约束。

3) EB 运行约束。

4) PtG 运行约束。

2.4.3 能源储存设备运行约束

储电设备受到容量和最大充放电约束，并且在同一时刻不允许充放电同时进行，为保证下个调度周期有可调节容量，首末时刻电量应相等。

式中Ee，t和Ee，t－1分别为t时段和t－1 时段储电设备的储电量;和Pdise，t分别为t时段储电设备的充、放电功率; βe为储电设备的容量;和ηdise分别为储电设备充、放电效率;和分别为储电设备的允许充放电功率的最大值;Ee，0和Ee，T分别为储电设备初始时刻和末尾时刻的电能占比;和udise，t为储电设备的状态变量为1 时说明储电设备正在充电，udise，t为1 时则处于放电状态，其他状态表示为0。

2.4.4 能源交易约束

为保证能源枢纽的收益，售给用户的能源价格应满足一定约束，过高会使用户用能成本过高，过低会让能源枢纽的收益难以得到保障; 同时能源经销商的能源售出价格也应满足一定约束，过高会使能源枢纽的能源购入量减小，过低会让能源经销商亏损。

3 博弈互动分析

博弈互动目标是追求能源经销商、能源枢纽和用户各自利益最大化的过程。Stackelberg 博弈唯一最优解为纳什均衡解。

在供给侧博弈中，能源经销商以利润FED最大决策出最优实时电价、最优实时气价，能源枢纽以收益FEH最大决策出最优电功率购入量、最优气功率购入量，直到博弈双方达到纳什均衡解。

在需求侧博弈中，能源枢纽以收益FEH最大决策出出售给用户的最优能源价格，用户以用能成本函数FEU最小决策出最优用能负荷大小，直到博弈双方达到纳什均衡解。

3.1 纳什均衡解存在且唯一证明

当Stackelberg 博弈模型满足以下条件时，则存在唯一的纳什均衡解［14］:

1) 博弈互动对象的取值空间为非空紧凸集;

2) 当博弈的领导者给定策略后，跟随者存在唯一最优策略;

3) 当博弈的跟随者给定策略后，领导者存在唯一最优策略。

根据各能源主体决策模型的约束条件式(13) ～式(19) 可知，各能源主体的决策变量都是有界、非空且紧凸，因此博弈模型满足条件1) 。

需求侧博弈中，用户用能成本函数FEU对用能负荷Lm，t求一阶偏导可得:

令上述一阶偏导等于0 得到用能负荷最优值:

将式(20) 再分别对Le，t、Lg，t和Lh，t求二阶偏导:

因为γm和Dm，t为正值，式( 22) 恒小于0，因此式(21) 为用户效益函数的极大值点。能源枢纽售能价格变化时，极值点可能位于负荷区间的边界上，但无论能源枢纽售能价格取值如何，可得唯一用能负荷最优解。

将最优用能负荷式(21) 代入能源枢纽收益函数式(7) ，再分别对λe、λg、λh求二阶偏导，可得:

式(23) 恒小于0，因此当用户用能负荷确定时，可得唯一能源枢纽售能价格最优解。

供给侧博弈与需求侧博弈同理，当能源经销商售电、售气价格确定时，可得唯一能源枢纽购能量最优解;当能源枢纽购能量确定时，可得能源经销商售电、售气价格唯一最优解，因此本文博弈模型满足条件2)和条件3) 。综上所述，所提Stackelberg 博弈模型存在唯一纳什均衡解。

3.2 求解方法

博弈互动交易模型目标是求解供需双侧各能源主体的纳什均衡解，实际上是求各能源主体目标函数曲线的交点。求解纳什均衡解的过程可理解为是将劣势策略不断淘汰后求得的最佳结果［15］。文中采用粒子群优化算法［16］求解纳什均衡解，求解过程可分为两步，第一步求解得到需求侧纳什均衡解，并将结果代入供给侧博弈互动交易模型中，第二步求解代入之后的供给侧模型得到供给侧纳什均衡解，再将供给侧纳什均衡解代入需求侧模型中循环求解，直到各能源主体利益变化满足条件为止。RIES 博弈求解流程图如图3 所示。

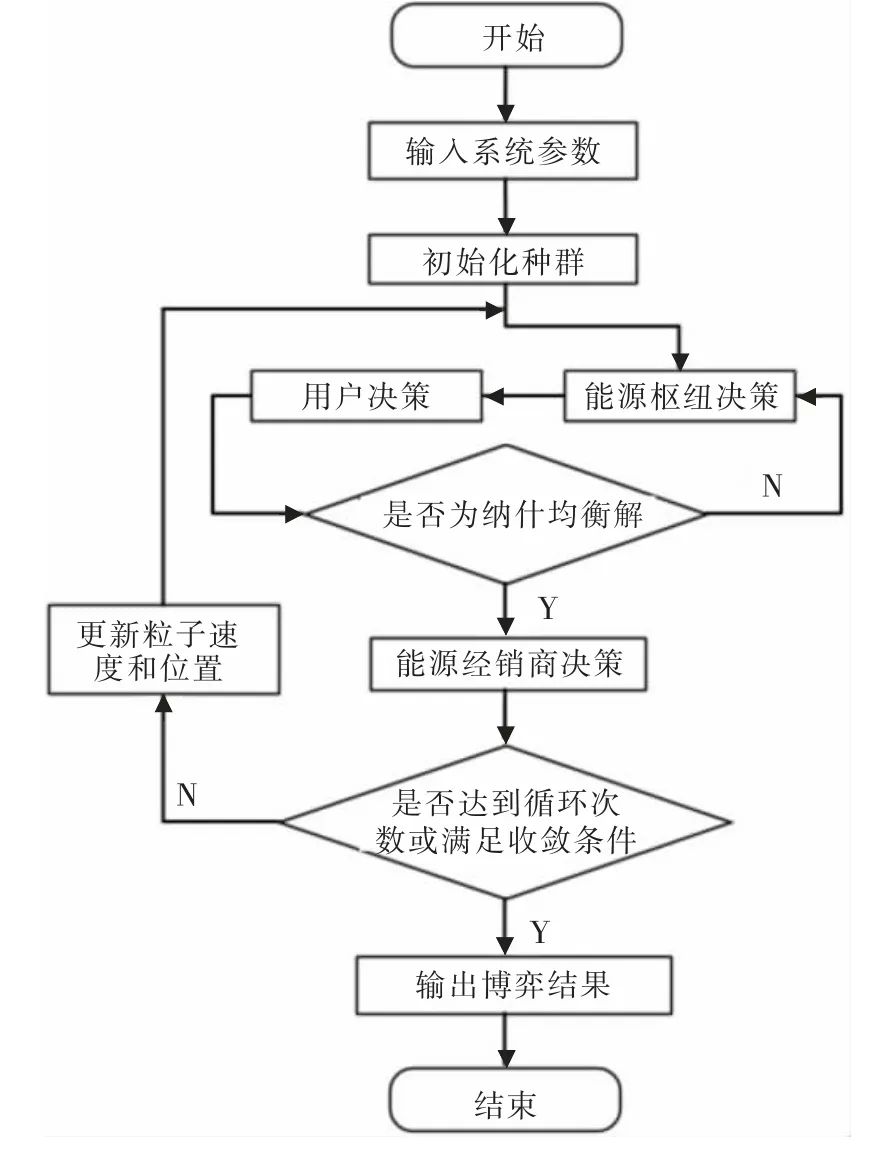
图3 RIES 博弈求解流程图Fig.3 Game solving flow chart of RIES

在求解流程中，外层循环采用粒子群优化算法对能源经销商售能价格和能源枢纽购能量进行优化，粒子适应度为能源经销商利益目标，适应度计算通过内层各主体的决策模型计算求得，采用CPLEX 求解器进行求解，以加快算法求解速度并保证结果的精确性。文中RIES 博弈求解步骤为:

步骤1:输入系统参数，包括RIES 各能源转换设备参数、风电和负荷预测数据等;

步骤2:初始化种群。生成能源经销商种群M，共M个粒子，粒子即表示能源经销商售能价格;生成能源枢纽种群N，共N个粒子，粒子即表示能源枢纽购能量;

需求侧博弈中双目标函数可见已经转化为式(24)单目标函数，自变量为能源枢纽售能价格λm，t，需满足式(19) 售能价格约束，其中λm，min和λm，max可表示为:

式中Lm，max和Lm，min分别为用户使用m类能源负荷的上下限。

需求侧博弈模型转化为上述单目标函数后，采用CPLEX 求解器进行求解得到需求侧纳什均衡解。

步骤4:在求解得到需求侧纳什均衡解之后，将需求侧的能源策略作为输入，粒子适应度为能源经销商的利润，进一步求解得到供给侧纳什均衡解。

其中，算法中粒子适应度函数表示为:

式中ck和Sk分别为第k轮循环时能源经销商的售能价格和能源枢纽的购能量;K为最大循环次数。

步骤5:直至达到循环次数或者粒子适应度满足收敛误差要求ε 时，循环结束。否则更新粒子的速度和位置，返回步骤3 进行下一轮迭代计算。

其中，粒子适应度收敛条件为:

步骤6:最后输出RIES 供需双侧博弈结果。

4 算例分析

4.1 算例概述

文中以冬季上海某地工业园区综合能源系统的典型日为例，RIES 系统结构如图1 所示，以全天24 h 进行日前交易决策，基于MATLAB2017a 平台进行仿真。用户侧各负荷需求和风电出力预测值见图4。RIES 中的各设备参数如表1 所示。储电设备的容量为2. 5 MW·h，充放效率为0.9，储电占比上下限分别为0.8和0.2，允许的最大充放电都为0.5 MW，运行维护费用为1.8 元·MW－1。能源经销商的发电机和天然气站运行费用系数如表2 所示。粒子群算法最大迭代次数为300，种群数量为100，收敛误差ε 为10－3。

表1 RIES 设备参数Tab.1 Parameters of units in RIES

表2 能源经销商机组运行成本系数Tab.2 Operating cost coefficient of energy dealer unit

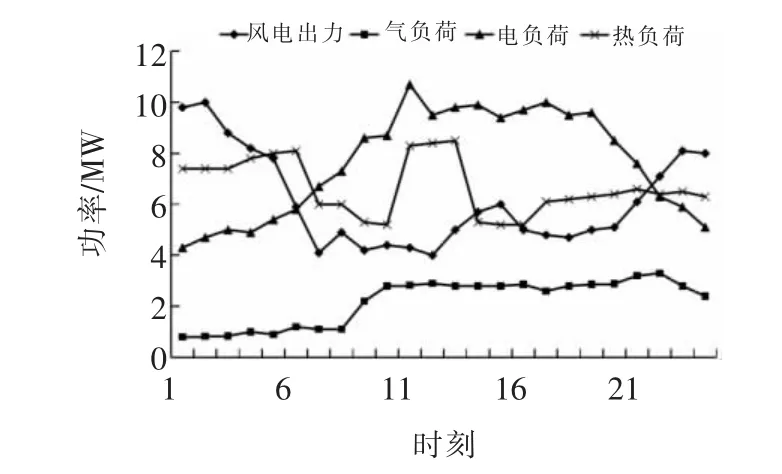
图4 负荷和风电出力预测Fig.4 Prediction of load and wind power output

4.2 结果分析

能源经销商和能源枢纽的售能收益优化迭代结果如图5 所示。博弈初期双方收益函数受到彼此能源策略的影响制约，互动双方的竞争比较激烈，导致售能收益曲线波动较大，第70 次博弈后，博弈已经取得纳什均衡解，售能收益已经收敛。当博弈得到纳什均衡解之后，双方的能源策略不在改变，在此策略下，任一能源主体都不能私自改变能源策略使得自身收益更高。最终，能源经销商与能源枢纽的售能收益分别为102357.7元和69789.2 元。

图5 售能收益优化结果Fig.5 Optimization results of energy sales revenue

能源经销商与能源枢纽的售能价格策略如图6 所示。虚线为各能源价格的上下限，可以看出各能源价格波动趋势与各类负荷变化趋势类似，如能源经销商售电价格和能源枢纽售电价格在11 h －13 h 和17 h －20 h出现两处峰值，这是为了刺激CHP 机组多发电，用户少用电，减少了能源枢纽向能源经销商的购电成本，从而增加收益。气价和热价与电价类似，此处不再赘述。

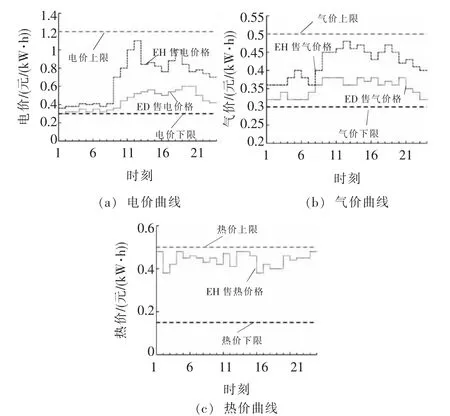
图6 售能价格曲线Fig.6 Energy sales price curve

图7为多种能源参与的能源枢纽供需双侧博弈得到均衡解之后的RIES 电、气、热能平衡结果。

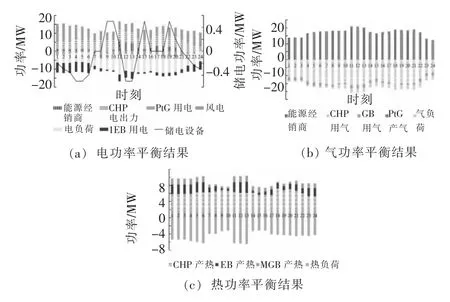
图7 RIES 功率平衡结果Fig.7 RIES power balance results

4.2.1 供给侧多能交易对博弈影响

文章通过4 个不同博弈场景来研究供给侧多种能源参与交易对能源枢纽与能源经销商收益造成的影响。场景一:能源经销商与能源枢纽之间存在电能、天然气博弈交易;场景二:能源经销商与能源枢纽之间存在电能博弈交易，能源经销商售气价格固定;场景三:能源经销商与能源枢纽之间存在天然气博弈交易，能源经销商售电价格固定;场景四:能源经销商给能源枢纽的售电价格、售气价格固定，两者不存在博弈互动。场景二～场景四中的能源固定售价取自场景一中对应能源的平均售价，以上所有场景均存在需求侧博弈互动。

表3 为4 个不同博弈场景下能源经销商与能源枢纽的收益对比。从表3 中可知，仅存在一种能源博弈交易的场景二、场景三对比能源价格完全固定的场景四，能源经销商和能源枢纽的收益更高; 同时存在电、气博弈交易的场景一中两者收益对比仅存在单一能源博弈的场景二、场景三更高，这是因为多种能源参与的博弈形式可以通过不同能源的替代和综合需求响应来实现能源间的协同优化配置。因此，所提的多种能源参与的供需双侧博弈互动模型具有较好的经济性。

表3 不同博弈场景下售能收益对比Tab.3 Comparison of energy sales revenue under different game scenarios

4.2.2 博弈互动下的RIES 调度分析

在1 h－5 h 和23 h －24 h，风电出力满足系统负荷，储电设备为充能状态，将多余电量储存，减少了弃风惩罚成本，利于系统的削峰填谷。在这一时间段内，由于能源经销商售电价格较低，能源枢纽向其购电，不足电量由CHP 机组提供，热能则主要有CHP 机组和EB 机组提供。在11 h－13 h，为了应对热负荷增大的情况，热电联产设备出力增加，能源枢纽购电量进一步增加。在10 h－20 h，用户用电需求较大，能源经销商售电价格高于售气价格，能源枢纽更倾向用CHP 机组产电和产热，热能不足部分则由EB 和GB 机组提供。而8 h－11 h、14 h－16 h 和18 h －21 h 时段电价较高时储电设备释放电能，储电设备的引入利于实现系统的灵活调度。

5 结束语

文章建立了基于供需双侧多能博弈互动的RIES优化模型，通过Stackelberg 博弈实现了能源枢纽与能源经销商以及用户之间的博弈互动，采用粒子群优化算法进行循环迭代求解，分析结果表明:

1) 建立的RIES 博弈互动策略存在纳什均衡解，且模型具有较好的收敛性;

2) 多种能源参与的博弈形式可以通过不同能源的替代和综合需求响应来实现能源间的协同优化配置，具有较好的经济性;

3) 能源枢纽中多种能源转换设备以及储电设备的引入能够使得各种能源间灵活转换，有利于实现源-荷-储协同优化运行。