轮胎侧偏刚度及力的特征函数的分析

王 君，陈仁全，孙 超，邱昌峰，周 磊，贾春辉，孙向阳，仇吉伟，张 超

（1.青岛双星轮胎工业有限公司，山东 青岛 266400；2.青岛轮云设计研究院有限责任公司，山东 青岛 266400；3.双星集团有限责任公司，山东 青岛 266400）

轮胎控制力主要表现在纵向的驱动力、制动力和侧向的转向力。通常，它们影响和作用于车辆的运动，特别是影响车辆的操控稳定性。操控稳定性、舒适性、直线牵引性能都是车辆动力学研究的重要的车辆性能[1-4]。其中，轮胎转向引起的车辆响应主要由轮胎与地面的相互作用产生的转向力控制。研究表明，车辆的不足转向严重影响车辆的操控稳定性，而不足转向的特性是由前后轮胎的侧偏刚度差来决定的。目前，自由滚动轮胎的力和力矩随侧偏角、侧倾角的变化能够充分描述轮胎力和力矩的特性，但是该方法不利于直接描述轮胎的动态特性[5]，因为轮胎稳态测试时力和力矩的变化需要逐点计算，同时轮胎测试的原始数据不能直接应用到特定的车辆中，需要进行简单的数据处理方法才能评估车辆的操控稳定性。

目前，特定车辆的操控稳定性以专业车手的主观性测评作为最终的评估，但是此方法受限于外界条件和人为因素。因此，本工作主要结合设计阶段的车辆模型和轮胎侧偏刚度的分析以及轮胎力的特征函数的数学解析方法，对车辆进行初步评估，从而调节轮胎参数和车辆的底盘参数，以提高车辆的操控稳定性，设计出最合理的方案。

1 实验

1.1 试验轮胎及试验设备

轮胎品牌为DOUBLESTAR，规格为205/50R17，速度级别为V，负荷指数为99。

试验设备为美国MTS公司生产的Flact Trac CT III型轮胎六分力试验机。

1.2 试验方法

按照GMW 15204—2007《轮胎稳态力和力矩测试》进行试验。试验条件为：环境温度 24 ℃，基准试验负荷 4 200 N，数据采集频率 1 024 Hz，轮胎速度 7.2 km·h-1，充气压力 230 kPa。

1.3 测试数据

轮胎力和力矩的测试步骤如表1所示。

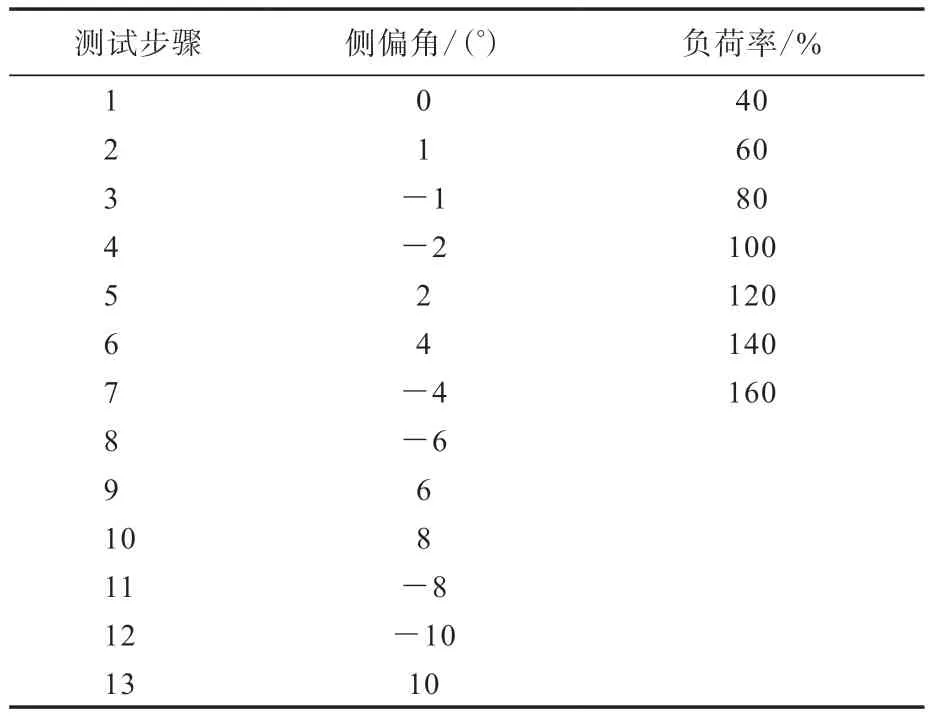
表1 轮胎力和力矩的测试步骤

从表1可以通过测试获得轮胎侧偏角、负荷与侧向力（Fy）的数据，绘制出数据地毯图。通过数据地毯图可以看出不同轮胎侧偏角、负荷以及侧向力的变化趋势，同时能够得到侧向力在线性区域及非线性区域的变化趋势。

2 轮胎侧偏刚度

车辆操控稳定性主要受到轮胎侧偏角、侧倾角、车辆速度以及垂直负荷作用下产生的侧向力和回正力矩的影响。轮胎力和力矩测试数据地毯图如图1所示。

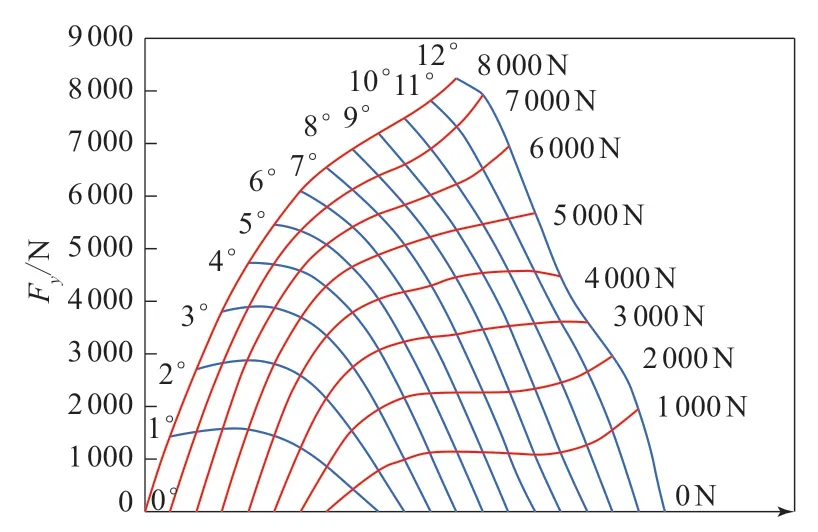
图1 轮胎力和力矩测试数据地毯图

从图1可以看出，小的侧偏角下，轮胎侧向力近似为轮胎侧偏角的函数，在任意负荷下，这种效应可以用轮胎侧向力和侧偏角的比例常数（侧偏刚度）来描述。根据SAE轮胎坐标系，正的侧偏角产生负的侧向力，因此侧偏刚度是侧向力相对于侧偏角导数的负值。在小的侧偏角下，轮胎的横向加速度很小，轮胎的横向负荷转移也很小，因此轮胎负荷接近于车辆作用下的平均负荷。

车辆左右轮胎的侧向力之和等于在相同侧偏角下轮胎平均负荷的两倍。因此在低的侧向加速度下，侧偏角和负荷对轮胎侧向力的影响可以用轮胎平均负荷下产生的侧偏刚度来描述。对于车辆给定的横向加速度，轮胎侧向力与车辆负荷成正比，关系如下：

式（1）可以转化为

由式（2）可知，侧偏角与车辆横向加速度成正比，与轮胎侧偏刚度和平均负荷的比值成反比。因此，随着轮胎侧偏刚度的增大，车辆在任何给定的横向加速度下所需的侧偏角减小，车辆转向时，力和力矩的响应较快，车辆操控稳定性能更好。

3 轮胎力的特征函数

3.1 轮胎侧向力系数

轮胎侧向力系数定义为：轮胎在基准试验负荷和一定侧偏角下的轮胎侧向力与基准试验负荷的比值[6]，公式如下：

式中，F（α）为轮胎侧向力系数，P为基准试验负荷。

在基准试验负荷下，不同侧偏角下的轮胎侧向力系数曲线如图2所示。

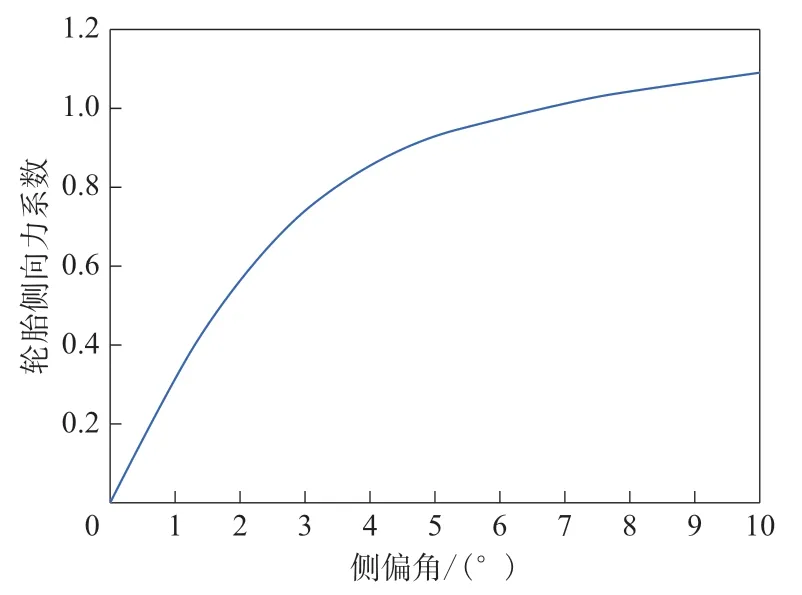
图2 不同侧偏角下的轮胎侧向力系数曲线

从图2可以看出，轮胎侧向力系数随着侧偏角的增大而增大。

经验表明，α＝1°时的F（α）[简称F（α＝1°）]是影响车辆在0～0.3g侧向加速度下操控稳定性的一个重要参数，F（α＝1°）越大，车辆的操控稳定性越好，反之，操控稳定性越差。因此，设计轮胎时可以通过改进轮胎的结构、花纹及配方，使F（α＝1°）增大，从而提升车辆的操控稳定性。

3.2 轮胎负荷灵敏度

轮胎负荷灵敏度定义为：在一定侧偏角下，轮胎在基准试验负荷与80%基准试验负荷时的侧向力差值与垂直负荷差值的比值，公式如下：

式中，H（α）为轮胎负荷灵敏度。

轮胎负荷灵敏度表征轮胎由于负荷的增大而导致其侧向力增大的能力。在基准试验负荷下，不同侧偏角下的轮胎负荷灵敏度曲线如图3所示。

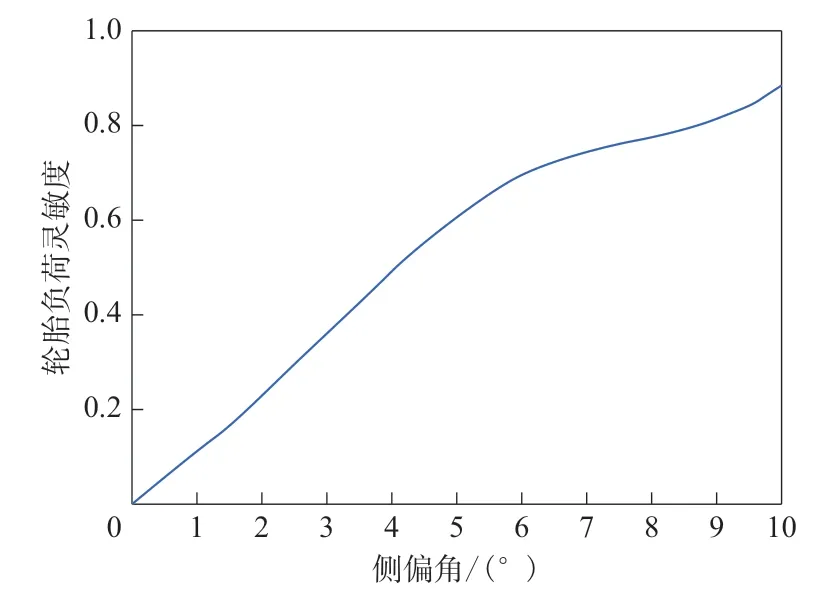
图3 不同侧偏角下的轮胎负荷灵敏度曲线

从图3可以看出，轮胎负荷灵敏度随着侧偏角的增大而增大。

经验表明，α＝1°时的H（α）[简称H（α＝1°）]是影响车辆操控稳定性的一个重要参数，H（α＝1°）越大，车辆的操控稳定性越好，反之，操控稳定性越差。一般轮胎设计人员可通过H（α＝1°）优化轮胎与车辆的匹配性，从而使车辆具有良好的操控稳定性。

3.3 轮胎负荷转移灵敏度

在大的侧偏角下，轮胎的力学特性不能用单一的参数进行描述，主要是由于车辆在特定侧向加速度下轮胎侧偏角的大小、单位侧向加速度下的侧偏角的变化以及轮胎横向负荷转移的影响都是非线性特性[7]。

在车辆行驶的过程中，如果忽略侧向负荷的转移，轮胎侧偏角与车辆侧向加速度的关系可以由车辆平均负荷的侧偏角与轮胎侧向力的特性来确定。当车辆在高速行驶中转动方向时，其左右两侧的轮胎存在负荷的侧向转移，从而影响车辆的稳定性。

为了更好地理解轮胎负荷转移的影响，当车轴上每个轮胎以2 500 N的平均负荷和4°的侧偏角行驶时，如果忽略负荷的转移，每个轮胎将产生2 597.7 N的侧向力；如果车轴存在1 500 N的负荷转移，则外侧车轮在4 000 N的负荷下行驶，内侧车轮在1 000 N的负荷下行驶，外侧车轮会产生3 732.7 N的侧向力，内侧车轮产生1 112.0 N的侧向力，每个轮胎的平均侧向力为2 422.4 N。因此，轮胎负荷的转移会造成轮胎侧向力的损失。

本工作分别在小负荷（2 500 N）和大负荷（6 500 N），负荷转移量为1 500 N，侧偏角为1°，2°，4°，6°，8°，10°下进行测试，从而得出不同侧偏角下轮胎负荷转移造成的侧向力的损失。

小负荷下，轮胎负荷转移造成的侧向力的损失公式为：

式中：F′y1为负荷转移下的轮胎平均侧向力；Fy1，Fy2，Fy3分别为1 000，4 000，2 500 N下的轮胎侧向力；F′y2为负荷转移下损失的轮胎侧向力。

大负荷下，轮胎负荷转移造成的侧向力的损失公式为：

式中，Fy4，Fy5，Fy6分别为5 000，8 000，6 500 N下的侧向力。

负荷转移灵敏度可以表示一对轮胎负荷转移（其中一条轮胎负荷增大，而另一条轮胎减小相同的负荷）的特征，其计算公式如下：

式中，G（α）为轮胎负荷转移灵敏度。

小负荷和大负荷下轮胎负荷转移测试结果分别如表2和3所示。

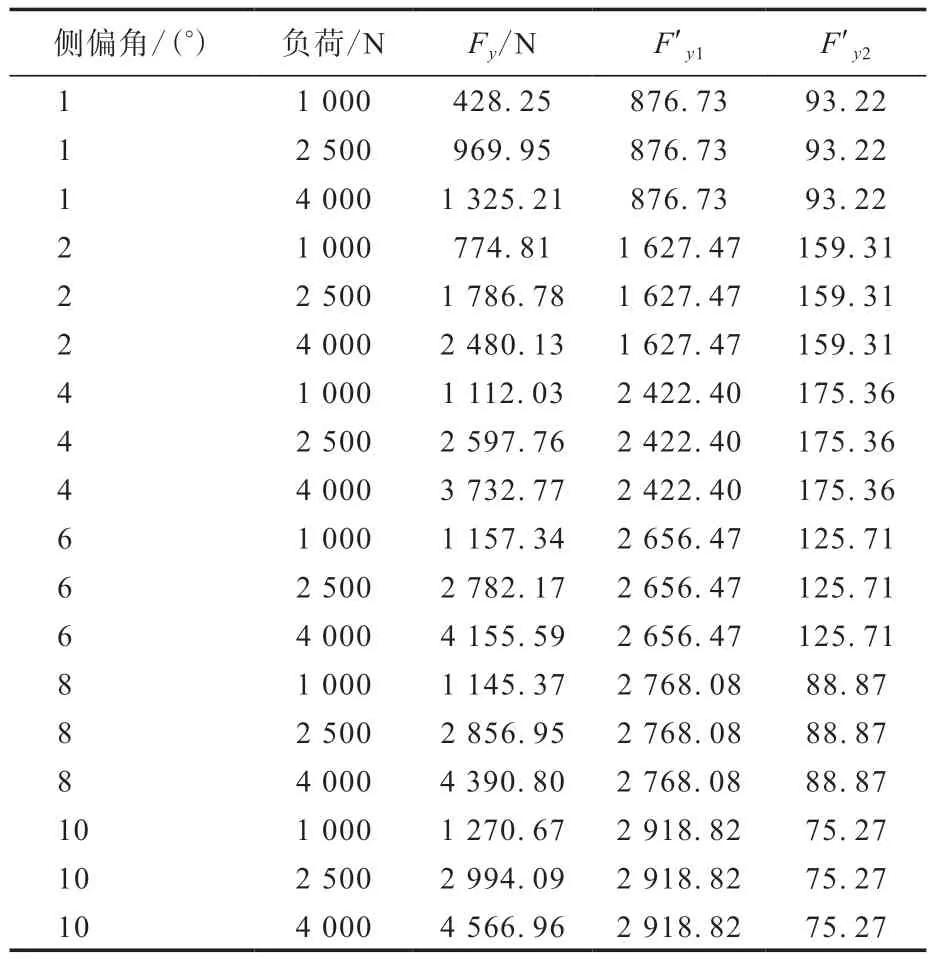
表2 小负荷下轮胎负荷转移测试结果

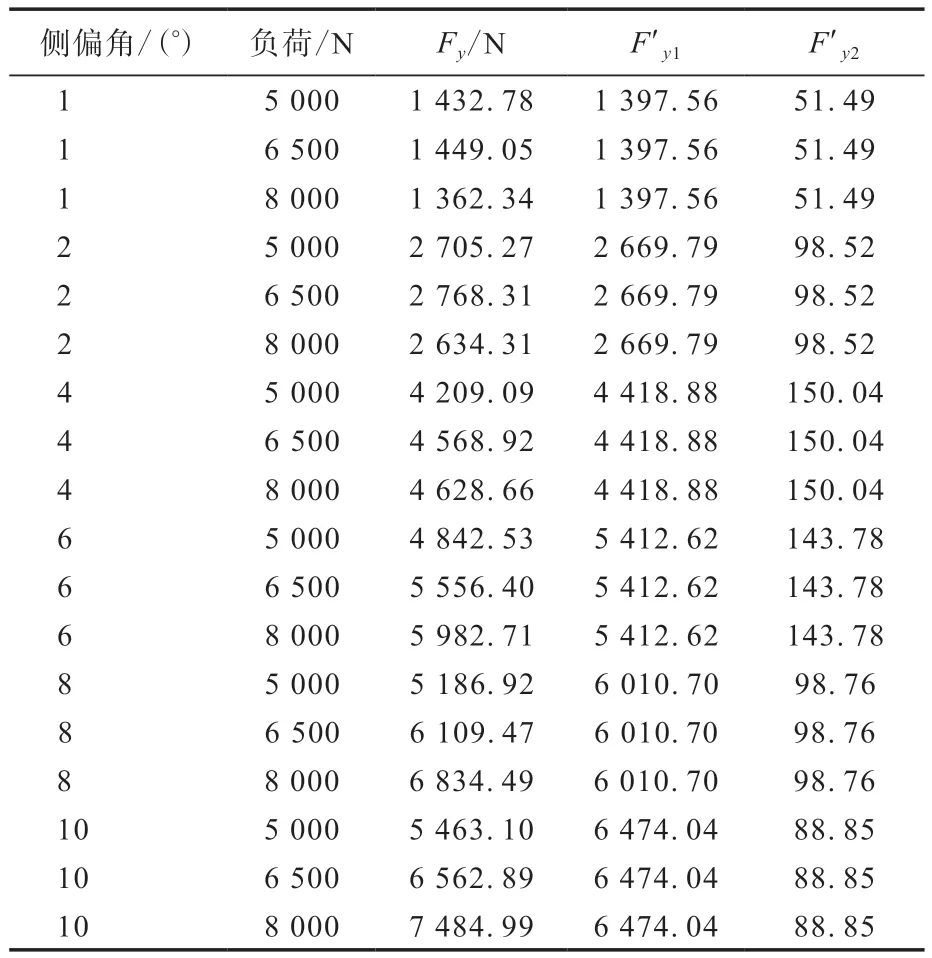
表3 大负荷下轮胎负荷转移测试结果

从表2和3可以得出在基准试验负荷和不同侧偏角下的轮胎负荷转移灵敏度曲线（见图4）。

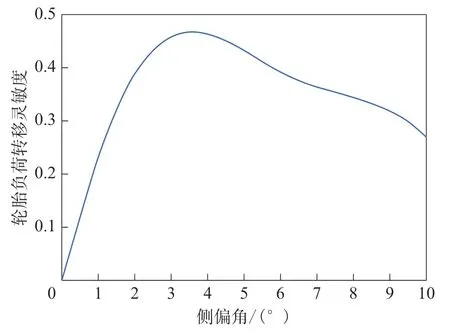
图4 不同侧偏角下的轮胎负荷转移灵敏度曲线

从表2，3和图4可以看出，无论在小负荷还是大负荷下，随着侧偏角的增大，侧向力的损失先增大后减小，在侧偏角为4°时，侧向力的损失接近最大，此时，轮胎负荷转移灵敏度可以表示为G（α＝4°）。

经验表明，G（α）在轮胎侧偏角和基准试验负荷的0.4倍到1.6倍进行评估，因此在计算G（α）时使用基准试验负荷的0.6倍可以准确地表示由于负荷转移而引起的轮胎侧向力的变化，如图5所示。

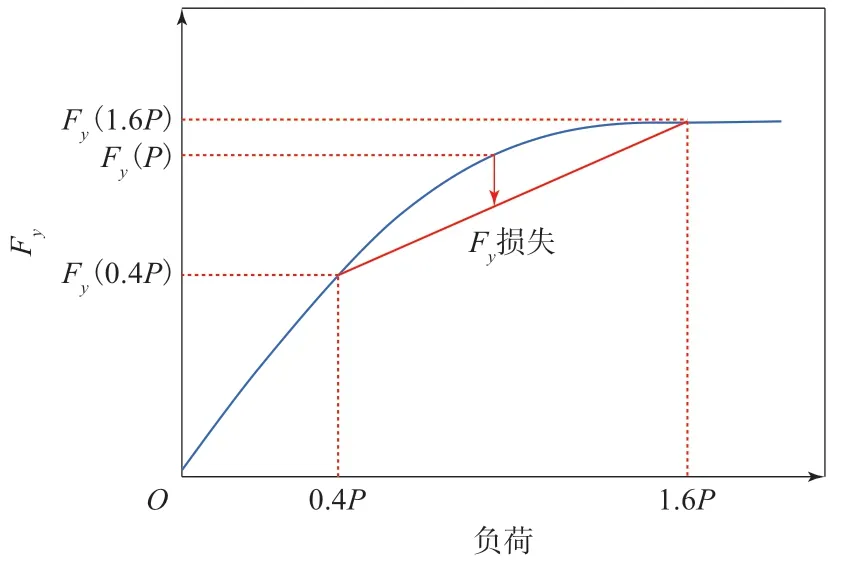
图5 负荷转移引起的轮胎侧向力的变化

4 轮胎侧偏特性对车辆操控稳定性影响

本工作采用的线性二自由度汽车模型如图6所示，图中：O为车辆质心；O′为车辆转向中心；x，y轴分别为车辆纵向和轴向坐标轴；v1为车辆质心速度；u，v分别为v1在x，y轴上的分量；β为质心侧偏角；W1为车辆横摆角速度；δ为前轮转角；α1，α2分别为前轮和后轮的侧偏角；a，b分别为车辆的前轴距和后轴距；L为车辆轴距；Fy11和Fy22分别为地面对前轮和后轮的侧向反作用力；u1，u2分别为汽车前轴和后轴中点的速度；ξ为u1和x轴的夹角。

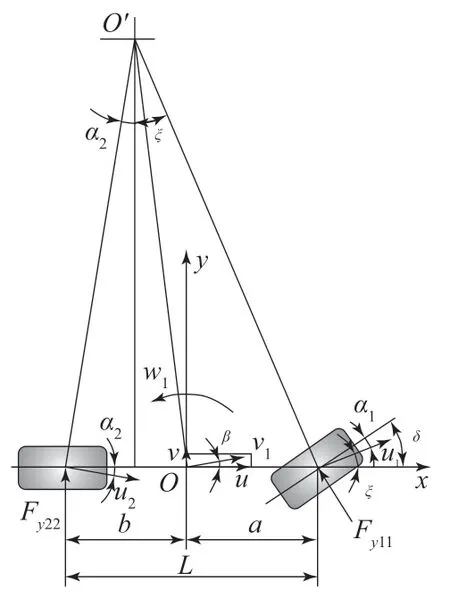
图6 线性二自由度汽车模型

本工作对前轮角输入的响应进行分析，对于转向车辆而言，车辆的转向角并不等同于轮胎的侧偏角，但在实验室采用六分力试验机测试时认为两者相同。

从图6可以看出，存在如下几何关系：

式中，R为车辆的转向半径。

由于通过车辆重心的侧向力惯性与轮胎的转向力相平衡，式（10）可以改写为

式中，Wf，Wr分别为车辆前后轴的负荷；Cαf，Cαr分别为车辆前后轴轮胎的侧偏刚度。

定义稳定性系数（K）为：

由式（12）可以得出：当K＞0时，车辆行驶处于不足转向；当K＝0时，车辆行驶处于中性转向；当K＜0时，车辆行驶处于过度转向。因此，车辆行驶中的稳定性系数主要依赖车辆前后轴的载重和轮胎的侧偏刚度，而轮胎的侧偏刚度主要受轮胎结构及充气压力变化的影响。目前提高车辆不足转向的方法主要如下：增大车辆后轮的充气压力，增大前轴负荷，采用较高侧偏刚度的后轮。

5 结论

（1）随着轮胎侧偏刚度的增大，车辆在任何给定横向加速度下所需的侧偏角减小，车辆转向时，力和力矩的响应较快，车辆操控稳定性能会更好。

（2）F（α＝1°）和H（α＝1°）数值越大，车辆操控稳定性的主观性测试结果越好，G（α＝4°）的数值越小，车辆因为负荷转移引起的轮胎侧向力损失越小，车辆的稳定性越好。在匹配轮胎和车辆的操控稳定性时，可以通过F（α＝1°），H（α＝1°），G（α＝4°）的特征值进行轮胎的结构、花纹、配方的优化，筛选出合理的轮胎设计方案。

（3）车辆稳定性系数越大，车辆不足转向性能越好。