高等数学教学设计探索与实践——以罗尔定理为例

李瑞芬

（金肯职业技术学院 江苏 南京 211156）

当前很多高职院校的高等数学课程教学依然延续传统的讲授模式，强调知识的系统性、严密性，而知识的实用性、文化性及趣味性却无法完全体现出来。2022 年5 月，新修订的《中华人民共和国职业教育法》正式施行，其中强调职业教育“立德树人、德技并修”的人才培养目标，将思想政治教育、职业道德教育、科学文化素养与专业技能培养放在同等重要的位置[1]。基于职业教育的理念与高职学生数学学习情况，高职数学教学更应注重学生综合素质与核心素养的培养。正如李大潜[2]所说，数学是一种先进的文化，数学教学体现了素质教育的精神。在实际教学过程中，要结合知识点蕴含的数学史、数学文化，挖掘学生感兴趣的元素，如此才能使学生爱学、想学，丰富学习内容，提高综合素养。

1 以素质教育为目标的罗尔定理教学实施

1.1 学情分析

微分中值定理理论性强，是教学难点。职业院校学生的基础知识薄弱，对学习缺乏兴趣与毅力，故增加了教学难度。因此，教师在讲授中值定理时应先联系生活，激发学生的学习兴趣，再充分理解定理的内容、证明、条件、应用，并在此过程中体会其中的数学方法。

1.2 教学目标

知识目标：掌握罗尔定理的条件、结论、几何意义及应用。

能力目标：锻炼学生分析问题的能力以及表达能力。

素质目标：培养学生的国家荣誉感、艰苦奋斗、科学精神，提升其综合素养。

1.3 教学重点与难点

罗尔定理的条件与应用是该教学的重点；罗尔定理的证明则是教学的难点。

1.4 教学方法

“讲授法”和“问题教学法”相结合，“互动式”和“启发式”交互进行，采用多媒体动画辅助教学。

1.5 教学过程

1.5.1 课程引入

引例：生活中的垂直上抛运动。乒乓球赛事中，要求发球员用手几乎垂直上抛乒乓球，当球从抛起的最高点下降时，发球员方可击球。乒乓球是我国的国球，通过该项运动可联想到奥运精神，奥运的精神更高、更快、更强在我国的乒乓球运动中得到完美体现。此时可播放视频，我国运动健儿发球和夺冠的精彩瞬间。

设计意图：通过观看视频激发学生的学习兴趣，培养学生的国家荣誉感与艰苦奋斗的精神。

实例：如图1，在某个位置垂直上抛一个物体，然后在同一位置把它接住。在这里，物体沿直线运动，设它的位移函数是x=f（t），物体在开始时刻t=a与结束时刻t=b处于同一位置，即f（a）=f（b），那么在时刻t=a和t=b之间，必定有这么一个时刻t=c，在该时刻，物体的速度为零，即f'（c）=0。这个结论成立吗？

图1 垂直上抛物体示意图

设计意图：此实例和引例对应，均为垂直上抛，垂直上抛运动是生活中出现的现象，数学来源于生活、应用于生活。这个结论的成立可以通过罗尔定理来验证，从而引出罗尔定理。

1.5.2 罗尔定理的定义

罗尔定理的条件：如果函数y=f（x）满足如下三个条件：①在闭区间[a，b]上连续；②在开区间（a，b）内可导；③在区间端点处的函数值相等，即f（a）=f（b）。接下来引导学生给出定理结果，教师可引导学生思考定理的三个条件分别对应什么样的图形特征，请学生看图观察，思考出定理的结论。其中条件①闭区间[a，b]上连续表示图形在区间上是连续不断的，不存在间断点。②在开区间（a，b）内可导表示图形在区间内是光滑的，没有尖点。③在区间端点处的函数值相等，表示函数图形在两个区间端点处到x 轴的高度一致，通过此分析，可以得出函数图形具有如下图2 形状。

图2 罗尔定理条件示意图

让学生观察图形并思考，从图形上能看到何种规律。学生很容易得出结论:左边的图形和右边的图形是中间图形的局部，均满足罗尔定理的条件。左边和右边的图形均有一条平行于x 轴的水平切线，中间的图形有两条平行于x轴的水平切线，因此得出结论：函数图形至少有一条水平切线，且此切线平行于x 轴。

设计意图：“互动式”和“启发式”相结合，激励了学生的学习主动性，同时也增强了学生对罗尔定理的记忆，更便于理解。

罗尔定理的完整表述是：如果函数满足如下三个条件：

①在闭区间[a，b]上连续；

②在开区间（a，b）内可导；

③在区间端点处的函数值相等，即f（a）=f（b），

结论是则在（a，b）内至少存在一点，使得f（'）=0。

1.5.3 罗尔定理的证明

启发式教学方式依然贯穿定理的证明过程，在授课过程中，教师可引导学生由果索因，定理的结论是要证明在区间（a，b）内存在一阶导数为0 的点。此时可以数形结合，如图2，通过图形观察：导数为0 的点可能是最大值点或者最小值点，但是函数在（a，b）内能否取到最大值和最小值呢？条件①告诉我们，函数在[a，b]上连续，闭区间上连续函数的最值性质又告诉我们，函数在闭区间上有最大值和最小值。接下来还有一个问题，最大值和最小值可能相等吗？相等是什么情况？不相等又是什么情况？从而可以得到：

若M=m，则f（x）在[a，b]上恒为常数，因此在（a，b）内，恒有f'（x）=0。

第二种可能，Mm的情况：因为端点函数值由图2 可以看出，最大值和最小值至少有一个不在端点处取得。那我们不妨设大M不在端点处取得，那么就应该在开区间内的某一个位置取得，也就是在（a，b）内必有一点即f（x）在处的值最大。在的邻域内，取一个增量依然在这个领域内，f（x）在处函数值最大，那么是小于等于0 的。所以当大于0时，这个增量之比小于等于0。小于0 时，这个增量之比大于等于0。

条件②告诉我们，f（x）在区间（a，b）内的任意点都可导，那在点当然可导，点的左右导数存在且相等。导数等于这个增量比也就是这个函数的极限。根据极限的局部保号性，左导数大于等于0，右导数小于等于0。因此点的导数等于0。这样，我们就分两种情况证明出了罗尔定理。

设计意图：以学生为主体的启发式教学模式，激发学生的学习兴趣，同时引导学生逻辑清晰的自主思考，将复杂的定理证明简单化，达到了教与学双向的良好效果。

接下来和引例对应，说明开始例子当中的位移函数就是定理中的函数时间间隔对应区间点对应时刻c。由罗尔定理的结论可知，在垂直抛球的过程中，必定有一时刻的速度为0。

1.5.4 罗尔定理的条件分析

罗尔定理的三个条件如果有任何一个不满足，结论都可能不成立，如

图3 例1 函数图象

分析：引导学生观察，f（x）是个分段函数，这个函数有如下特点：在（0，1）内可导，两端点函数值相等，但f（x）在X=1处不连续，故不满足罗尔定理的条件①。从图中也容易看出在（0，1）内不存在导数等于0 的点。事实上，可以求出在（0，1）内，f（x）的导数等于1。

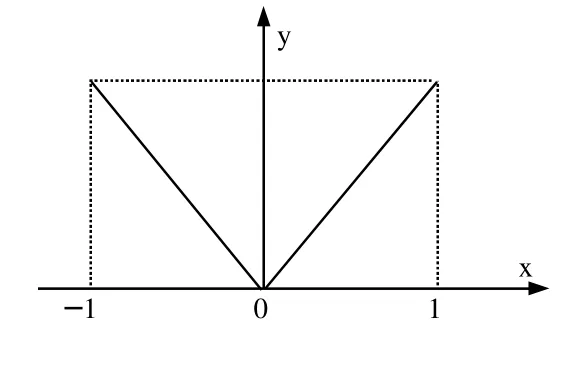
图4 例2 函数图象

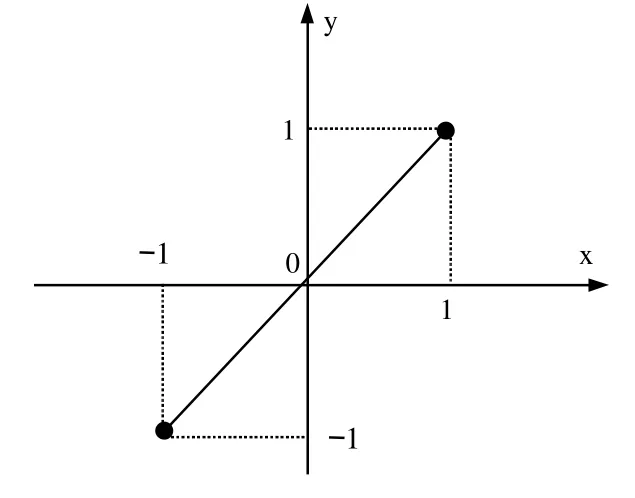
图5 例3 函数图象

设计意图：上述三个例子验证了罗尔定理的三个条件如果有一个不满足，结论可能不成立。即可能找不到使f'（）=0 的点。此三个例题放在一起，分别从定理的三个条件出发，体现了解决问题过程中考虑问题的严谨性、全面性，有助于学生考虑问题时良好习惯的养成。

那能不能认为，如果定理的三个条件不全成立时，一定找不到导数为0 的点呢？我们再来看这样一个例题：

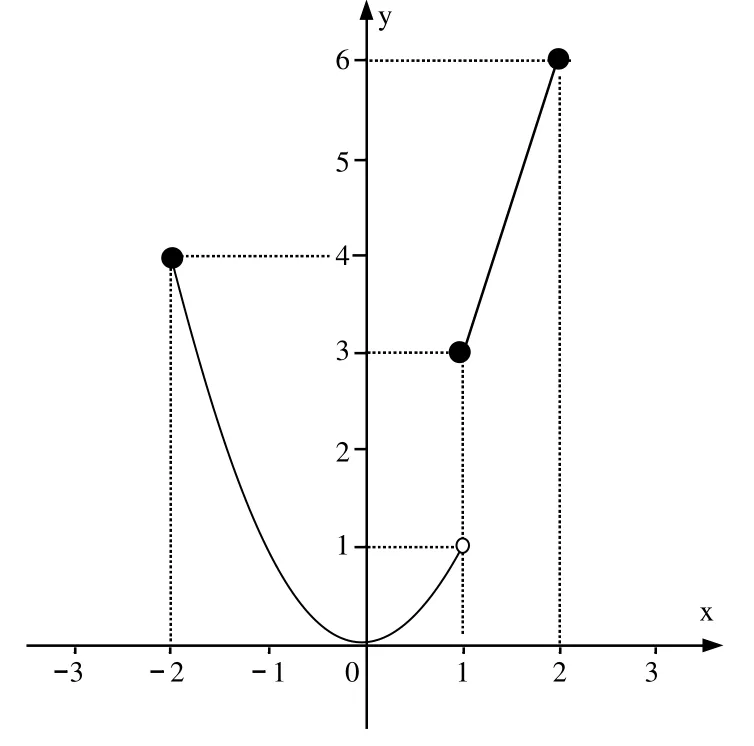
图6 例4 函数图形

分析：引导学生观察，f（x）在[-2，2]上有定义，在x=1处不连续，从而也不可导，两端点函数值也就是说，这里罗尔定理的三个条件均不满足。而我们容易看出，x=0处，f'（0）=0。由此可见，罗尔定理的三个条件，不是结论成立的必要条件，而是充分条件。

设计意图：全面理解罗尔定理的三个条件，解决问题时不仅要考虑问题的充分条件，还要考虑是否为必要条件。考虑问题时不仅要探究问题的广度，深度也同样重要，至此发散学生思维，提高其综合素质。

1.5.5 巩固提高

例5：设f（x）满足以下条件：（1）f（x）在闭区间0,a上连续；（2）f（x）在0,a内可导；（3）f（a）=0；证明：在0,a内至少存在一点，满足

1.2.6 定理的起源

1691 年，法国数学家罗尔在论文《任意次方程的一个解法的证明》中提出，这个多项式方程的两个相邻实根中间，另一个方程至少有一个实根，这个定理是罗尔定理的前身。罗尔当时对微积分的正确性提出了质疑，故此定理的证明方法是纯代数的。一百多年后，意大利数学家贝拉维蒂斯提出了现在的罗尔定理。由于此定理是建立在罗尔提出的定理的基础之上，故贝拉维蒂斯将此定理命名为罗尔定理。

设计意图：讲解罗尔定理的起源，学习科学家的探索精神和诚实谦逊的优良品德。

2 教学反思

学习完“罗尔定理”后，学生做了相关的练习题和调查问卷，总体反映学习效果较好，虽然定理的证明稍难，但是通过教师的引导与启发式教学还是能理解掌握，故本次教学设计符合高职院校学生的学情，教学理念较为新颖，教学方法合理。教学设计中，特别是上课开始引入的乒乓球运动和奥运夺冠瞬间的视频能激发学生的学习兴趣，培养学生的国家荣誉感与艰苦奋斗的精神。课堂中，教师层层递进，抽丝剥茧，能有效引导学生积极参与，认真思考，在此过程中学生能感受到知识点的整体性和学习相应的数学方法。此种教学设计不仅可以提高学生的数学思维，也提高了其综合素质，培养了学生的综合素养。

3 总结与展望

高等数学是一门抽象的学科，这种特点使学生在学习的过程中感觉难度大，因此，在教学过程中合理地使用引导式与启发式的教学方法尤为重要。且提高数学核心素养与解决问题的能力是学生学习教学的主要目的。引导式与启发式的教学方式更能激发学生学习兴趣，提升其学习主动性，从而培养出会思考问题，能解决问题的学生，提高学生的综合素养。