新工科背景下高等数学案例教学设计

周晓杰

（大连大学信息工程学院 辽宁 大连 116622）

2017 年以来，教育部积极推进新工科建设，奏响“复旦共识、天大行动、北京指南”三部曲。新工科建设以立德树人为引领，培养面向未来的创新型卓越工程人才[1]。作为理工科的一门重要基础课，高等数学不但是很多工科专业课程的知识基础，也承担着培养学生科学精神、提升其分析问题和解决问题能力的重要任务。因此，面对新工科建设的机遇与挑战，高等数学教学应做出适当的改革。

教育部2015 年发布的《关于加强专业学位研究生案例教学和联合培养基地建设的意见》文件指出，案例教学是以学生为中心，以案例为基础，通过呈现案例情境，将理论与实践紧密结合，引导学生发现问题、分析问题、解决问题，从而掌握理论、形成观点、提高能力的一种教学方式[2]。案例教学法在法律、医学、工商管理等学科教学中的成功促使我们探索其在大学高等数学教学中的应用[3-4]。

1 案例法引入高等数学教学的意义

1.1 案例教学法能激发学生的学习兴趣

作为地方性普通本科院校，大连大学学生的高考数学成绩普遍不高。以2022 年某理工科专业为例，忽略各省高考试卷的不同，单从分数来看，该专业高考数学平均分仅为91.3 分，不及格率为41.5%，相当一部分同学反映数学是其弱势科目，多年的数学学习以及长期学习受挫的经历磨灭了学生的学习兴趣。通过引入案例教学法，将抽象的理论和专业问题以及生活实际结合起来，让学生认识到数学的应用价值，更能激发学生的学习兴趣。

1.2 案例教学法是以学生为中心理念的体现

传统的高等数学教学侧重讲授概念、性质、定理等理论知识，以及帮助学生理解这些理论的例题及习题。在这个过程中，以教师为主体，学生处于被动接受的地位。而采用案例教学法，通过创设情境，学生主动思考，参与其中，在“做中学”，更能体现以学生为中心的教学理念。在案例教学的过程中，培养学生分析问题、解决问题的能力及创新能力，使学生掌握面向未来的本领，这也是以学生发展为中心教学理念的体现。

1.3 案例教学法有利于课程思政目标的实现

在当前“大思政”的背景下，如何将“全过程育人，全方位育人”的思政元素融入具体的教学设计当中，是每门课程都面临的问题。课程思政讲求“润物细无声”，如“盐溶于水”，在潜移默化中对学生进行正确的价值引导。而如果为了思政而思政，生硬地展示思政元素则可能产生适得其反的效果。采用案例教学，可将思政元素融于案例中、融入故事中，进而相对更好地实现课程思政的育人目标。

2 高等数学案例的整体教学设计

在充分分析高等数学课程的内容及教学要求的基础上，我们收集整理了教学案例库，主要包含概念引入型案例和数学应用型案例，并将思政教学目标融入其中。教材采用大连理工大学出版的《工科数学分析》，全书共九章，案例教学整体实施方案见表1。

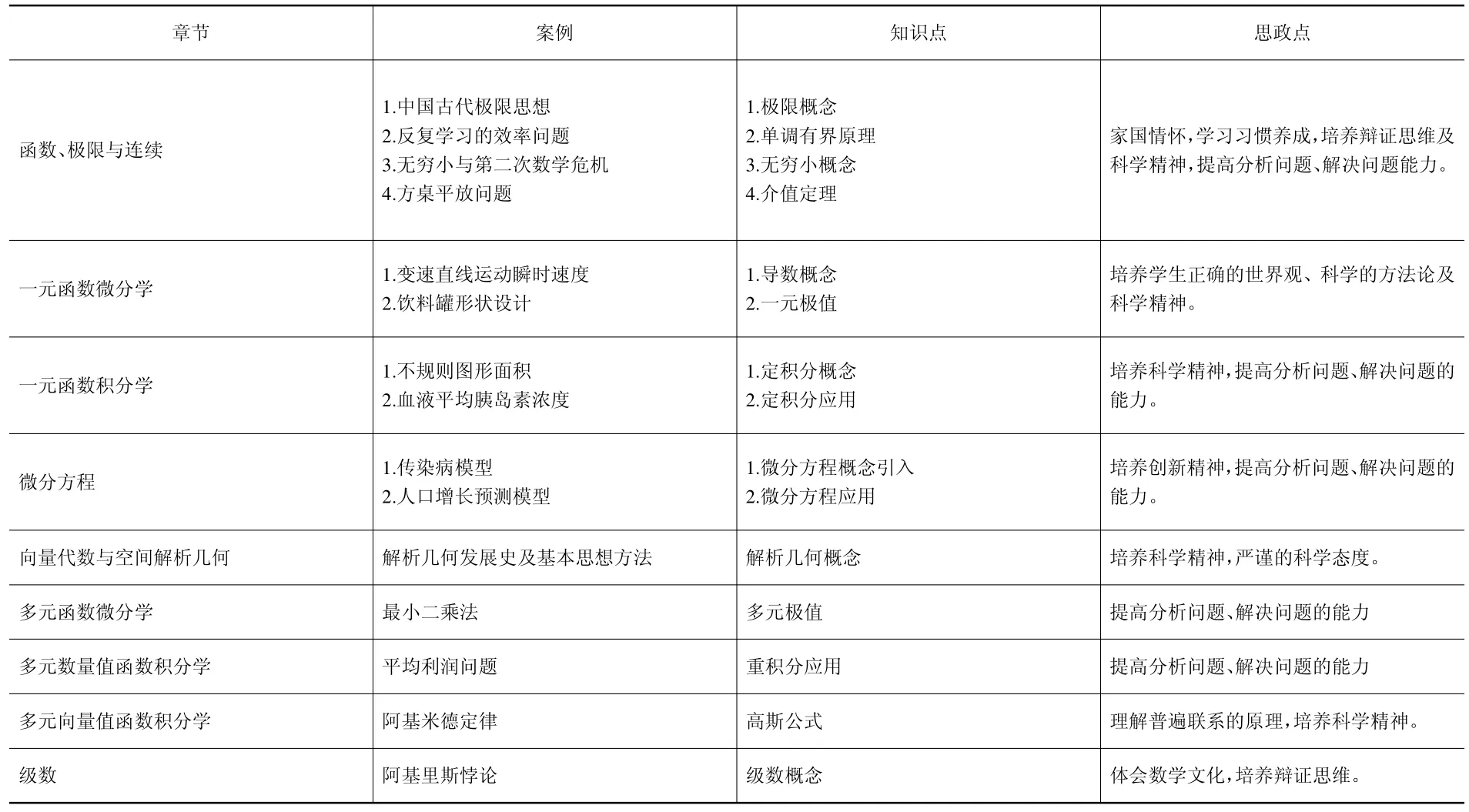
表1 案例教学整体实施方案

3 案例教学举例

本节以高等数学第一章极限部分单调有界原理内容为例，介绍案例教学法的具体实施过程。

3.1 教学分析

经过前面内容的学习，学生已经能够理解极限概念的思想及定义，会用极限的四则运算法则及复合函数极限运算法则计算简单的极限。单调有界原理是一个重要的极限存在准则，也是证明第二重要极限的基础，需要学生理解其内涵并会应用其解决实际问题。刚入大学的学生容易延续高中数学的学习方法，注意力主要放在如何做题上，因此教师宜多培养学生主动思考及分析问题的能力。本节内容的教学重点是对单调有界原理的理解及运用，教学难点是通过案例培养学生分析问题和解决问题的能力。

3.2 教学目标

知识目标：理解单调有界原理的内容，会用单调有界原理解决数列极限问题。能力目标：培养学生分析问题、解决问题的能力。素质目标：培养学生的数学思维和严谨的作风，提高学生的数学素养，引导学生养成孜孜以求的奋斗精神。

3.3 教学方法

以案例教学法为主导，通过案例问题，采用启发式的教学模式，引导学生分析问题，对实际问题进行建模，将其转化为一个数学问题。采用“数形结合”的思想帮助学生理解。

3.4 教学过程

3.4.1 案例引入

心理学研究指出，任何一种新技能的获得和提高都要经过一定时间的学习。我们经常有这样的经历，两人学习某项技能，经过相同时间的学习后，他们对该技能的掌握程度可能有较大的差异，这种现象是如何产生的呢？能否用数学方法加以解释[5]？

3.4.2 案例分析

学习是一个积累的过程，技能的掌握程度不但与学习者的初始掌握程度及学习时间有关，也与其自身的学习效率密切相关。假设b0为开始学习时的技能掌握程度，A 表示经过一次学习之后所掌握的程度，即每次学习所掌握的内容占未掌握内容的百分比。

下面探究数学模型的建立，通过启发式教学与学生共同建立模型。

记bn为经过n次学习后所掌握的程度。则1b0就是第一次学习时尚未掌握的新内容，经过一次学习掌握的新内容为A1b0，于是b1b0=A1=b0，类似有b2b1=A1b1。以此类推，得到经过n次学习后所掌握的程度为bn+1bn=A1bn,n=0，1，2，…，即

bn+1= 1A bn+A，n=0，1，2，

于是，将该技能掌握程度表示成一个数列，通过分析数列，即可得到想要的结论。

3.4.3 案例求解

探究数列特点，可以首先用数形结合的方法，将数列可视化来进行观察。不妨假设b0=0，分别取A为不同值，观察数列的情况如图1。

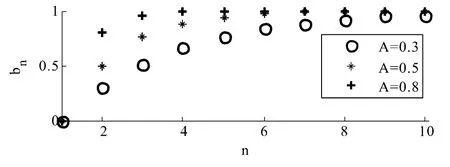
图1 数列元素图示

从图像观察得知：无论A的取值如何，数列都是单调递增的，而且随n着的增大，无限趋近于1，即由此引出单调有界原理这个知识点，并通过数形结合的思想具体讲解两种情况：若数列单调递增且有上界或单调递减且有下界，则该数列必有极限。

回到原问题，从上述建立的数学模型可知，经过同样时间的学习过程，不同的人技能掌握程度产生差异主要是因为学习效率的不同。若掌握95%以上的学习内容则认为该技能基本掌握，则学习效率A=0.8 的同学只需要两次学习即可达到，而A=0.3 的同学则需要9 次学习才能达到。虽然过程不同，但只要通过足够次数的学习都能达到掌握知识的目的，殊途同归。由此我们还可以看出，随着学习的进行，掌握速度越来越慢，入门容易，深入钻研难，要追求卓越就要发扬孜孜以求的奋斗精神。

3.4.4 数学扩展

为了锻炼学生的数学能力，可以用典型的极限问题来讲解单调有界原理的应用。例如，1996 年高等数学考研题：设x1=10，，试证数列{xn}极限存在，并求此极限。做题的同时可以引导学生总结利用单调有界原理解决极限问题的常用情形及具体应用方法。

3.4.5 思考

最后给出两个思考题：①在实际学习过程中，一般要考虑两种机制：知识的获得和知识的遗忘，在此机制下，模型又该如何建立？②若用模型刻画知识的记忆程度，考虑艾宾浩斯记忆曲线，模型又该如何改进？思考题供有余力的同学进行钻研，可进一步提升学生的创新能力。

3.5 教学反思

本小节的教学采用案例教学法，使学生聚焦于分析问题、解决问题的情境中，能够在教师的引导下主动思考，在解决问题的过程中掌握单调有界原理这一知识，并能潜移默化地对学生进行价值引领，实现了预期的教学目标。

4 结语

在高等数学的教学中采用案例教学法，可以提升学生的学习兴趣，培养学生的分析问题、解决问题的能力和创新能力。本文通过单调有界原理小节的教学具体阐述了案例教学的过程及效果。后续还将继续收集教学案例，做好案例教学学时与讲授学时的分配，编制基于案例教学的课程整体教学设计及教学单元设计，力争实现案例教学成效最大化。