高精度单脉冲角度跟踪新方法

张凤珊，陈 拓，陈晓燕，蒋 阳，曾 浩

（1.北京卫星信息工程研究所，北京 100086；2.重庆大学 微电子与通信工程学院，重庆 400044）

0 引言

在雷达、通信、测控等领域中，采用基于相控阵天线的幅度和差单脉冲测角技术被广泛用于目标角度跟踪，具体又分为查表法和公式法[1]。查表法需要建立每一个跟踪轴角度下的差和比曲线，天线测量过程复杂，存储资源消耗大，访问速度慢。而公式法只需要根据子波束接收信号幅度计算目标角度，克服了查表法的不足，所以本文讨论公式法。根据文献[1]，公式法误差来源主要有两个，一是子波束接收信号的幅度估计误差，二是改变波束指向导致的方向图畸变误差。

来波信号的幅度估计是公式法的重要步骤，幅度估计精度将直接影响到目标测角精度，估计方法主要有最大似然估计[2-3]、能量公式估计[4]等方法。利用最大似然法检测强背景噪声中的信号已经成为比较成熟的方法，并得到广泛应用，但该方法要求有用信号已知，并非真正意义上的盲估计算法[5]。利用能量公式法估计信号幅度的复杂度低，且在高信噪比（Signal-to-Noise Ratio,SNR）下幅度估计精度高，但在低SNR 下，易受到噪声的影响。如果可以降低接收信号中的噪声，提高信噪比，那么能量公式法将是一种复杂度低、但估计精度高的幅度估计方法。

另一方面，为了减小方向图畸变对测角的影响，相关学者对此展开了广泛的研究。文献[6-9]通过引入线性约束条件，减小差和比曲线畸变的问题，但约束条件繁琐、复杂。文献[10]建立一种误差补偿的神经网络模型，通过神经网络算法来对差和比曲线进行补偿，但学习复杂度高且样本依赖性严重。文献[11]提出了一种独立于和波束的数字差波束形成方法，相比于传统方法，测角精度提高了1.16 倍。文献[12]提出一种基于虚拟子阵的目标角度估计方法，它将阵列划分为两个虚拟子阵，并利用测量值的相位差来估计目标角度，但涉及矩阵求逆和积分运算，不利于硬件实现。文献[13]提出一种基于扩展卡尔曼滤波的单脉冲角度跟踪方法，其算法鲁棒性高，但很难建立运动目标的精确运动模型，且模型线性化过程复杂。文献[14]针对二维测角方法存在角度估计耦合的问题，提出了一种解耦测角方法。

针对上述问题，本文采用循环位移自相关方法来降低噪声对信号的影响，并利用复杂度低的能量公式估计来波信号幅度。此外，本文利用同心圆环阵在结构上的对称性，从而保持天线的波束形状和增益基本不变[15-16]，最终减小改变波束指向导致的方向图畸变误差。从这两个方面减小误差来源，提高目标角度估计精度。

1 阵列接收信号模型

假设一个具有M层圆环的同心圆环阵，各个圆环半径ρm沿径向依次递增，Nm表示第m层圆环的阵元个数。进一步假设第m层圆环的第n个阵元的方位角为ψmn，其示意图如图1 所示。

图1 同心圆环阵的阵元分布图

由于均匀同心圆环阵需要满足阵元在各个圆环上等间距分布且其相邻圆环间距相等的要求，因此均匀同心圆环阵的阵元方位角位置ψmn、圆环半径ρm和阵元数Nm的计算公式如下：

式中：Δρ表示相邻圆环之间的间距，λ表示来波信号波长。进一步假设窄带远场平面波信号入射俯仰角θs和方位角φs，根据圆心处的阵元接收到的信号：

则第m层圆环的第n个阵元的接收信号可以表示为

式中：m(t) 表示信号复包络，ω表示信号角频率，τmn(θs,φs)表示第m层圆环的第n个阵元相对于圆心阵元接收信号的延时：

由于接收信号一般含有噪声，因此可定义阵列接收信号矩阵为：

式中：V(θs,φs)表示信号方向矩阵，如式（6）所示；N(t)表示噪声矩阵，各个单元噪声独立同分布。

根据和差波束设置，接收机采用数字加权方式同时形成4 个不同指向子波束。记子波束指向为(θ0,φ0)，则对应的权值矩阵为：

此时波束指向(θ0,φ0)的同心圆环阵的波束输出信号为：

式中：W*表示W的共轭，符号“◦”表示两个同阶矩阵的Hadamard 积，sum[]表示求矩阵所有元素的和。d(t)表示不含噪声的子波束输出信号，n(t)表示输出信号中的噪声。

2 二次循环位移自相关幅度估计

幅度和差单脉冲测角技术需要估计子波束接收信号幅度，而带内噪声和杂波是影响估计精度的主要因素。如果接收信号是周期信号，通过循环位移自相关序列进行信号幅度估计，可以使非期望信号（包括带内噪声和杂波）的影响大大减小。

假设子波束接收信号y(t)采样后的离散序列y(k)，其自相关函数ry(m)为：

式中：K表示快拍数，m∈[1-K,K-1]。根据式(8)，ry(m)可以进一步表示为：

式中：rd(m)、rn(m)分别表示期望信号d(k)、非期望信号n(k)的自相关函数，rdn(m)、rnd(m)表示两者互相关函数。根据信号统计特性可知：如果噪声和杂波均为非相关信号，那么rdn(m)、rnd(m)均为零，且rn(m)为Delta 函数。假设d(k)是周期信号，则rd(m)是一个与原信号同周期的函数，幅度大小恒定且由待估计量，即信号d(k)的幅度A决定。显然，对于新的序列ry(m)，由于噪声和杂波的影响仅仅在m=0 一个位置，那么用m≠0 的剩余ry(m)进行幅度估计就可以克服非相关噪声和杂波的影响。

实际上，子波束输出信号y(k)的长度K是有限的，此时ry(m)的幅度不再是定值，而是随着m模值的增大而减小。为了保证ry(m)的幅度基本不变，从而能够高效估计A，本文引入循环位移[4]的概念，即先把序列y(k)进行周期延拓，得到周期为K的新序列：

符号mod(k,K)表示对序号k进行模K运算，再按照自相关定义式（9）计算得到新自相关序列：

不同于ry(m)，循环位移自相关rz(m)的幅度基本上是恒定的，并由A决定。需要注意的是，K的取值不是任意的，K值必须保证周期延拓后的序列在拼接点处相位是连续的。

rz(m)的噪声是由于有限快拍导致的期望与噪声、杂波的互相关rdn(m)和rnd(m)不为零。相同的原理，通过对rz(m)做二次循环位移自相关处理，可以进一步消除噪声和杂波对信号的影响，即取长度为K的rz(m)进行周期延拓，得到：

然后再计算自相关函数：

根据上述分析，如果期望信号d(k)是一个正弦波，对rr(k) 可采用复杂度低的能量公式来估计信号幅度A，即：

3 和差单脉冲测角方法

3.1 子波束建立方法

假设跟踪轴的波束指向角度为(θ0,φ0)，四个子波束的波束指向角度与跟踪轴的俯仰偏角均为θk，方位偏角均为φk。根据前文对阵列权值的表示，四个子波束权值分别为：

进一步假设目标角度为(θs,φs)，目标偏离跟踪轴的俯仰角为θt、方位角为φt，如图2 所示。规定目标在跟踪轴的下侧时θt为正，目标在跟踪轴的右侧时φt为正，显然有：

图2 幅度和差单脉冲测角示意图

如果波束指向跟踪轴的相控阵天线幅度方向图函数为：

根据圆环阵列几何布局特点，幅度方向图函数E(θ,φ)在四个子波束方向具有相同的值，即：

相比于均匀平面阵列，由于同心圆环阵在结构上的对称性，使得式（19）中的四个表达式之间的误差更小，最终导致基于同心圆环阵模型的测角误差更小。

3.2 差和比计算

文献[11]和文献[14]介绍了差和比计算方法的两种经典方法，都可以采用本文提出的幅度估计方法和阵列结构。文献[11]利用阵列法向方向矢量构建方向图函数，文献[14]则直接利用跟踪轴方向矢量，此处仅仅讨论后者。

根据文献[14]，和波束信号幅度、差波束信号幅度，作比得到俯仰维的差和比曲线Sθ(θs)和方位维的差和比曲线Sφ(φs)，即：

式中：

3.3 算法步骤

（1）对来波信号粗捕获，估计得到的目标大致角度(θ0,φ0)，并将该角度作为幅度和差单脉冲测角方法的跟踪轴指向角度。

（2）根据θk、φk以及跟踪轴指向角度(θ0,φ0)，确定四个子波束的波束指向角度，并同时产生四个相应波束指向的子波束。

（3）根据四个子波束的接收信号，采用第2 节的二次循环位移自相关方法估计得到四个子波束的接收信号幅度。

（4）根据式（20）、式（21）计算得到俯仰维的差和比值和方位维的差和比值。

（5）根据式（20）、式（21）分别估计得到目标信号角度。

4 算法复杂度分析

平面阵列模型和信号幅度估计的能量公式法是目前单脉冲相控阵角度跟踪的基本方法，而采用圆环阵列和二次循环位移自相关是本文新方法。这些方法都可以同文献[11]和文献[14]两种经典差和比计算方法结合。为此，定义6 种单脉冲测角方法，并按照表1 关系命名，其对应计算量如表2 所示。

表1 不同方法的解释说明

表2 不同方法计算复杂度对比

比较方法11 和方法21，两种算法复杂度相当，且都不高。但一旦采用二次循环位移自相关方法，则计算量明显增加。此外，相比等面积平面阵，圆环阵的计算复杂度会随着单元数L增加而增加。可以看出，本文所提方法23 是以计算复杂度为代价提高角度跟踪精度。

5 仿真校验

5.1 实验设置

以中低轨道的机载卫通角度跟踪为背景，假设接收点频信号的频率为70 MHz，采样频率为300 MHz，SNR为-10 dB。采用1 024 个快拍数据进行目标角度估计，并做M=500 次蒙特卡罗实验。进一步假设同心圆环阵的圆环层数为5 层，通过式（1）计算同心圆环阵的总单元数，然后开方取整得到均匀平面阵的天线单元行、列数。假设跟踪轴指向角度为(30°,150°)，跟踪轴与四个子波束指向的俯仰偏角θk、方位偏角φk均为3 dB 带宽的一半，目标偏离跟踪轴的俯仰角为2°、方位角为1°。

为了对各算法进行评价，采用角度估计值的均方根误差（Root Mean Square Error,RMSE）来评价算法的测角精度：

式中：θ、φ分别表示目标真实俯仰角、方位角；分别表示第m次目标角度估计值；θRMSE、φRMSE分别表示目标俯仰角估计值、方位角估计值的RMSE。

5.2 循环位移自相关去噪

仿真参数如5.1 节的实验设置所示。对含有噪声的子波束输出信号进行自相关和二次循环位移自相关，其结果如图3 所示。

图3 自相关和循环位移自相关去噪结果

图3 中，横坐标表示采样序号，纵坐标表示信号幅度。从图3（c）可以看出，输出信号的自相关函数的幅度随采样序号的增大而减小，而其二次循环位移自相关函数是幅度基本不变的周期函数，且与原信号具有相同的周期，如图3（d）所示。这说明循环位移自相关方法能够降低信号中的噪声。

5.3 测角精度影响因素分析

现在对来波信号进行角度估计，并分析信噪比SNR、阵列层数M、跟踪轴的方位指向角度φ0和目标偏离跟踪轴的方位角φt这四个因素对测角精度的影响。

5.3.1 SNR 对测角精度的影响

设定SNR 从-25 dB 到10 dB 均匀变化，步长为1 dB，其余参数和5.1 节保持一致。从而六种方法的角度估计RMSE 曲线如图4 所示。

图4 SNR 对测角精度的影响

在中低轨道的机载卫通角度跟踪背景下，接收机的SNR 水平一般在-25 dB 到0 dB。从图4 可以看出，当SNR 为-25 dB 时，本文所提出的方法23 的测角精度是最高的，其空间角度误差不到1°。进一步观察可知，随着SNR 的增大，所有方法的测角RMSE 均会减小，当SNR 足够大时，测角误差收敛。但对于任意SNR，方法23 的测角精度都是最高的。

进一步分析图中曲线，还可以得到如下结论：其他条件一样时，文献[14]差和比计算方法优于文献[11]方法，采用二次循环位移自相关估计幅度方法优于传统能量公式法，采用圆环阵列方法优于平面阵列。这也是本文方法误差最小的原因。

5.3.2 阵列层数对测角精度的影响

设定同心圆环阵的阵列层数M从2 到10 均匀变化，步长为1。由于θt、φt不能超过方向图的3 dB 带宽的一半，因此设定θt、φt均为1°。其余参数和5.1 节保持一致。从而六种方法的角度估计RMSE 曲线如图5 所示。

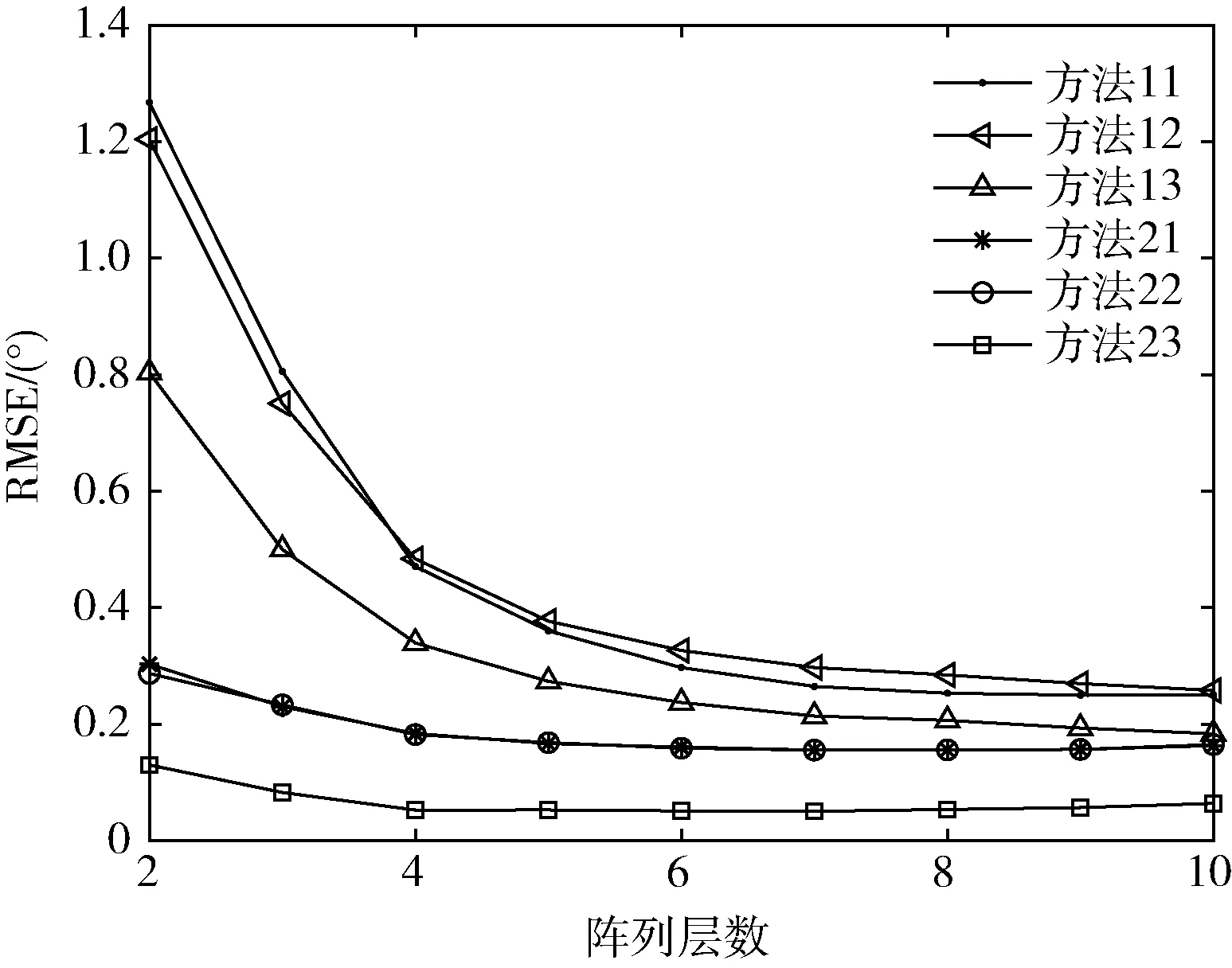
图5 阵列层数对测角精度的影响

从图5 可以看出，随着阵列层数的增加，即对应天线单元数的增加，所有方法的测角RMSE 均会减小。这是因为阵元数越多，方向图的3 dB 带宽就越窄，从而差和比曲线的斜率就越大，测角灵敏度就越高，最终使得测角精度越高。对于任意阵列层数，方法23 即本文方法的测角精度都是最高的，而且可以得到与5.3.1 相同结论。

5.3.3 跟踪轴角度对测角精度的影响

设定跟踪轴的俯仰角θ0固定为30°，方位角φ0从0°到360°变化，步长为10°。其余参数和5.1 节保持一致。从而六种方法的角度估计RMSE 曲线如图6 所示。

图6 跟踪轴角度对测角精度的影响

从图6 可以看出，由于同心圆环阵在结构上的对称性，使得当跟踪轴的波束指向角度发生改变时，其方向图形状基本保持不变，从而使得测角RMSE 基本不变。而基于均匀平面阵模型的测角方法由于改变波束指向导致方向图畸变严重，最终使得测角RMSE 增大。但由于均匀平面阵也具有一定的对称性，因此其测角误差呈现出一定的周期性。进一步观察可知，方法23 即本文方法几乎在整个角域的测角精度都是最高的，而且同样可以得到与5.3.1 相同结论。

5.3.4 φt 对测角精度的影响

设定φt从0°到2°均匀变化，步长为0.2°。其余参数和5.1 节保持一致。从而六种方法的角度估计RMSE 曲线如图7 所示。

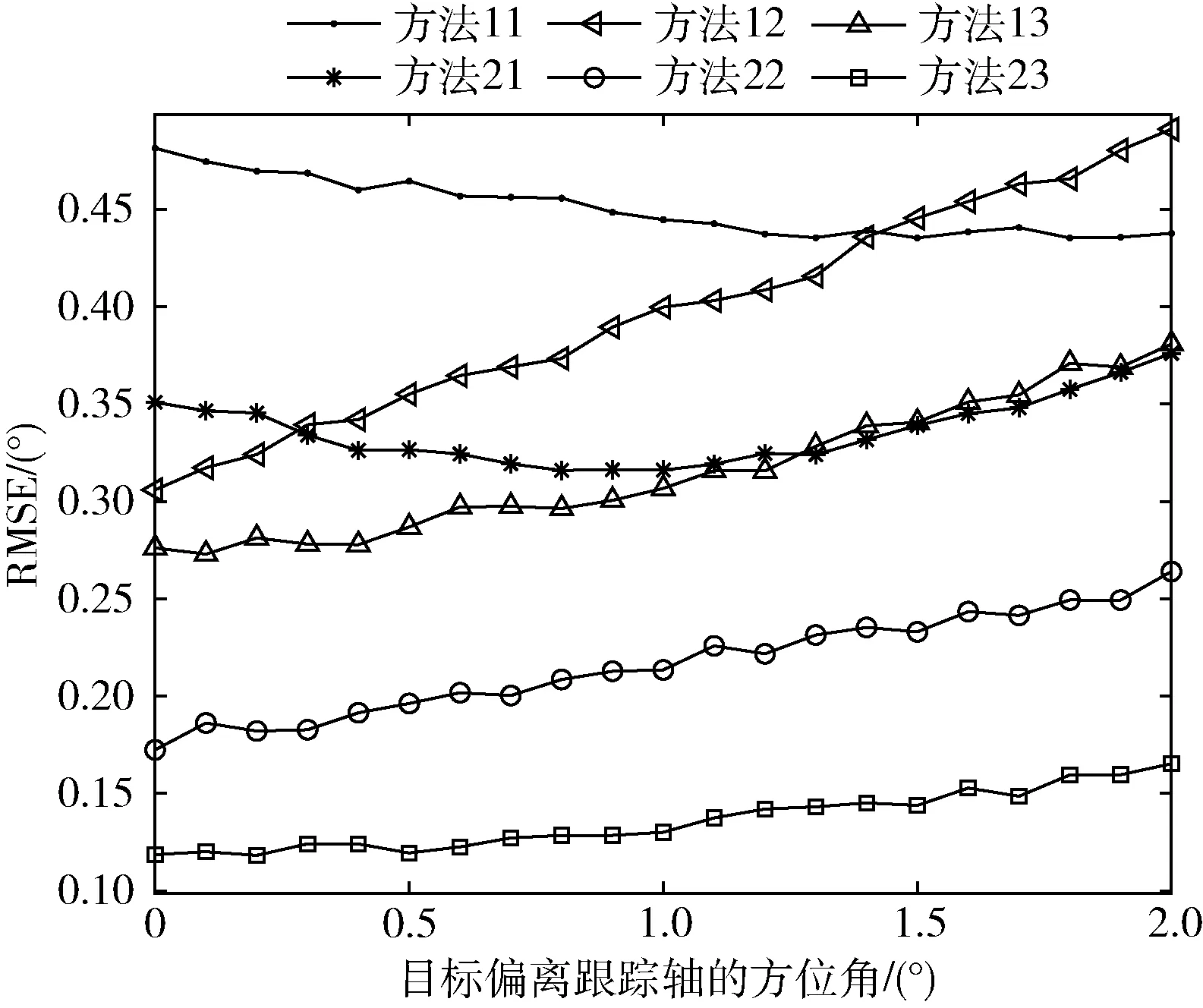
图7 φt 对测角精度的影响

从图7 可以看出，随着φt的增大，除了采用能量公式法估计信号幅度的方法11 和方法21 之外，其余方法的测角RMSE 均会增大。这是因为如果目标偏离跟踪轴越远，那么四个子波束接收信号的SNR 就越低，且受方向图畸变的影响就越大，最终导致测角RMSE 增大。进一步观察可知，对于任意目标偏离跟踪轴的方位角角度，方法23 即本文方法的测角精度都是最高的，这时5.3.1 相同结论还是成立。

6 结论

本文基于相控阵天线基本理论，利用同心圆环阵在结构上的对称性，减小改变波束指向导致的方向图畸变误差。进一步利用循环位移自相关方法降低信号中的噪声，并采用复杂度低的能量公式估计信号幅度。从这两个方面减小误差来源，提高目标角度估计精度。本文方法算法简单，存储空间小，实时性高，可以应用于对目标角度测量有需求的领域。