具有防御能力的Variable-Territory捕食模型平衡态正解分析*
武阳鸽,王利娟,杨 帆,金 露
(宝鸡文理学院 数学与信息科学学院,陕西 宝鸡 721013)
ANDREWS对抑制性基质下的微生物生长进行数学建模时,提出了一种Monod-Haldane型功能反应函数(简称M-H函数)来刻画抑制性基质对微生物的抑制效应,其表达式为φ(S)=S/(m+kS+S2),其中S表示具有抑制性的培养液浓度,k表示抑制常数,m=kkS,kS为微生物的比生长率,表示单位时间内单位质量的微生物所增加的数量[1]。近年来,众多学者在研究捕食模型时发现食饵会对捕食者产生防御现象,这种现象与抑制性基质对微生物的抑制作用相似,因此M-H函数也被广泛用于食饵具有防御能力的捕食模型中[2-7]。其中文献[2]在具有脉冲收获和放养的两物种ODE捕食模型中引入M-H函数,利用Lyapunov函数研究物种灭绝的条件。文献[3]在经典的Lotka-Volterra捕食PDE模型中引入M-H函数,研究了生长率对平衡态正解多重性、稳定性和唯一性的影响。文献[4]在一类年龄依赖的捕食模型中引入M-H函数,研究了模型非负稳态解的存在性和唯一性条件。文献[5]研究了带有M-H反应项捕食模型分歧解的性质,给出了系统分歧解存在和稳定的充分条件。文献[6]研究了由2个猎物和1个捕食者组成的具有M-H和Holling II型功能反应函数的捕食模型,给出了模型正解持久性、局部稳定性和全局稳定性条件。文献[7]研究了基于营养-浮游生物的捕食模型,利用M-H型功能反应函数模拟浮游生物释放毒素的过程,给出了正解的Hopf分岔及其方向、稳定性等结果。另一方面,捕食者也会依据食饵密度来调节自己的捕食效能。如文献[8]提出捕食效能与食饵密度成反比的Variable-Territory捕食模型,并称这种现象为捕食者具有自控能力(self-limitation)。在此基础上,文献[9-11]在齐次Neumann边界条件下研究了一类具有线性功能反应函数的Variable-Territory捕食模型,分析了正常数解的稳定性和渐近行为,非常数正解的存在性和渐近行为。文献[12-13]在齐次Dirichlet边界条件下研究了具有Holling II型的Variable-Territory捕食模型,利用连续延拓技术、分歧理论和扰动理论研究了模型正解的存在性、稳定性以及唯一性。文献[14]在齐次Dirichlet边界条件下研究了一类小扰动下的Variable-Territory捕食模型,利用不动点指数理论建立了正解存在和不存在的充分条件。
本文将利用Monod-Haldane型功能反应函数模拟食饵的防御能力,在齐次Dirichlet边界条件下研究如下Variable-Territory捕食模型
(1)

(2)

(3)
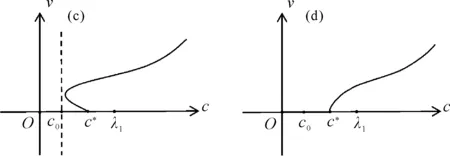
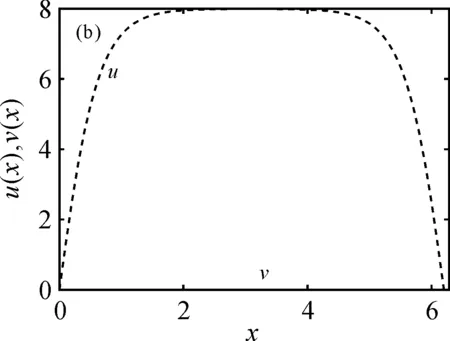
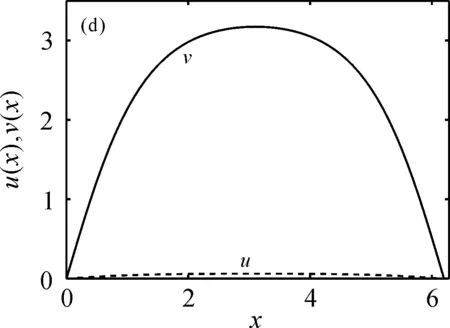
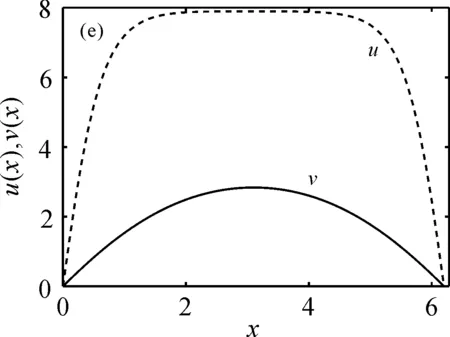
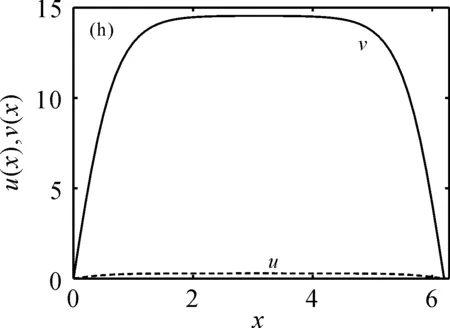
的唯一正解,且0<θa 定义如下特征值问题 (4) 下面给出模型(2)正解存在的必要条件和先验估计。 证明若(u,v)是模型(2)的正解,那么u>0,v>0,x∈(0,l)。 (ⅰ)证明a>λ1。 在模型(2)中第一个方程左右两边同乘以φ1,并在(0,l)上积分得 再由格林公式整理可得 因此a>λ1。 记h=a-u,将u=a-h代入模型(2)中第一个方程,则h满足 有 由于a>λ1,那么(3)有唯一正解θa,因为 u(a-u),x∈(0,l), 所以u是方程(3)的严格下解。又a是方程(3)的严格上解,且u 由于 对上式左右两边同乘以φ1,并在(0,l)上积分得 再由格林公式和φ1>0,可得 (ⅳ)证明m>a2时,c>c*。 在模型(2)的第二个方程两边同乘以χ1,并在(0,l)上积分得 利用格林公式整理得 由m>a2可得 故c>c*。 进一步,可以给出问题(4)中c*的估计式。 定理2设a>λ1,则 证明(1)利用θa的性质以及特征值的单调性即可证明。 左边取下确界得 利用θa g∈C1[0,l],g>0,x∈(0,l), (5) 在模型(2)中,令ω=θa-u,χ=v,则(ω,χ)满足 (6) 其中, 显然N1(0,0)=N2(0,0)=0,D(ω,χ)N1|(0,0)=D(ω,χ)N2|(0,0)=0。 L(c,ω,χ)= 那么结合引理1知L:R×X→X是紧的连续可微算子。记G(c,ω,χ)=(ω,χ)T-L(c,ω,χ)。因此G(c,ω,χ)=0,0≤w≤θa,χ≥0当且仅当(u,v)是模型(2)的非负解。 定理3设a>λ1,则(c*,0,0)是G(c,ω,χ)=0的一个分歧点,也就是说,在(c*,θa,0)的邻域内模型(2)至少存在一个正解。 证明令L1(c*,0,0)=D(ω,χ)G(c*,0,0),L2(c*,0,0)=Dc(ω,χ)G(c*,0,0)。通过计算得 令L1(c*,0,0)(ω,χ)T=0,则 所以N(L1(c*,0,0))=span{(ω1,χ1)T}。另一方面,L1(c*,0,0)的伴随算子为 因此codimR(L1(c*,0,0))=1。 下证L2(c*,0,0)(ω1,χ1)T∉R(L1(c*,0,0))。因为L2(c*,0,0)(ω1,χ1)T=(0,-Kχ1)T,假设存在(ω0,χ0)∈X,满足L1(c*,0,0)(ω0,χ0)=L2(c*,0,0)(ω1,χ1),即(ω0,χ0)满足 在上述第二个方程两端同乘以χ1,并在(0,l)上积分可得 利用格林公式可得 不妨取 Z=R(L1(c*,0,0))= 显然X=Z⊕N(L1(c*,0,0))。 由文献[16]中的局部分歧定理可得,(c*,0,0)是G(c,ω,χ)=0的一个分歧点,即存在ε>0和一条连续可微曲线(c(τ),ρ(τ),π(τ)):(-ε,ε)→R×Z,使得c(0)=c*,ρ(0)=π(0)=0且有 (c(τ),ω(τ),χ(τ))= (c(τ),τ(ω1+ρ(τ)),τ(χ1+π(τ))), 使G(c(τ),ω(τ),χ(τ))=0。记u(τ)=θa-τ(ω1+ρ(τ)),v(τ)=τ(χ1+π(τ)),那么(c(τ),u(τ),v(τ))(|τ|<ε)是模型(2)的解。若取0<τ<ε,则它恰为模型(2)的正解。记 Γ={(c(τ);u(τ),v(τ)):|τ|<ε}, 则分歧点(c*,θa,0)附近的非平凡非负解要么在分支{(c;θa,0):c∈R}上,要么在分支Γ上。 在第2节已经给出了局部分歧解的存在性,现在利用Fredholm算子的全局分歧理论把局部分歧解延拓为全局分歧解。由定理3的证明可知L1(c*,0,0)是一个指标为零的Fredholm算子,利用文献[17]Theorem 4.4(或文献[18]Theorem 1.2)可得到包含如下集合 S={(c,ω,χ)∈ R+×X:G(c,ω,χ)=0,(ω,χ)≠(0,0)} 的一个连通分支C,并且C要么在R+×X上是不紧的,要么包含点(c,0,0),其中c≠c*。记 P1={u∈C1(0,l):u>0, x∈(0,l);u′(0)>0,u′(l)<0}, P={(c,u,v)∈R+×X,u,v∈P1}, C′={(c,u,v):u=θa-ω,v=χ,(c,ω,χ)∈C}。 定义正解分支与负解分支分别为 易知Γ+⊂C′,Γ-⊂C′,且C′∩P≠∅。令C*=C′∩P,则C*在分歧点(c*,θa,0)附近包含局部正解分支Γ+。取C+是C′Γ-的连通分支,易知C*⊂C+,根据文献[17]Theorem 4.4(或者文献[18]Theorem 1.2)可知C+满足下列选择之一: (ⅰ)C+在R+×X中不紧; (ⅲ)C+包含形如(c,θa+u,v)的点,其中(u,v)≠(0,0),(u,v)∈Z。 由此可知(ⅱ)和(ⅲ)都不成立,故只能是(ⅰ)成立,则C+是无界的或C+-{(c*,θa,0)}⊄P。由于C+-{(c*,θa,0)}⊂P,故C+是无界的。 由定理1知, 由Lp估计和Sobolev嵌入定理,存在常数M,N>0,使得‖u‖C1 通过以上分析可得模型(2)局部分歧解的全局结构。 定理4若a>λ1,则模型(2)存在一个从点(c*,θa,0)发出的连续正分支解C*={(c,u,v)}⊂P,它包含了定理3中给出的局部正分支曲线Γ+,且C*在P内或者沿参数c延伸到∞或者沿c-v面延伸到∞。进而当a>λ1,c>c*时,模型(2)存在正解。 定理5设m>a2,则模型(2)存在正解的充分必要条件是a>λ1,c>c*。 证明由定理1可得必要性,由定理4可得充分性。 注1由M-H函数意义可知参数m=kkS,这里k表示防御系数,kS表示食饵的比生长率。故定理5表明,当食饵的防御系数k与食饵比生长率kS之积大于食饵生长率的平方时,食饵与捕食者可以共存的充要条件是它们的生长率适当大。 注2由定理2知c0 图1 全局正分歧解的示意图Fig. 1 The diagram graph of the global positive bifurcation solution 本节讨论定理3给出的正分支解的局部稳定性。令X1=[C2,α(0,l)×C2,α(0,l)]∩X,Y=Cα(0,l)×Cα(0,l),α∈(0,1),i:X1→Y是包含映射。设L是模型(2)在(c*,θa,0)的线性化算子,则由定理3的证明可知, 又因为i(-ω1,χ1)∉R(L),所以0是L的i-单重特征值。 引理20是L的实部最大的特征值。 证明由于0是L的特征值,所以只需证明0是实部最大的特征值。假设λ0是L实部大于0的特征值,(φ,ψ)为对应的特征函数,则L(φ,ψ)T=λ0(φ,ψ)T,即 由引理2和线性算子稳定性理论知,在c*和0的邻域内存在C1函数c→(κ(c),μ(c))∈R×X1和τ→(ξ(τ),σ(τ))∈R×X1,使得 (κ(c*),μ(c*))= (0,(-ω1,χ1))=(ξ(0),σ(0)), 并且 L(c,θa,0)μ(c)=κ(c)μ(c),|c-c*|≪1, L(c(τ),u(τ),v(τ))σ(τ)=ξ(τ)σ(τ),0<τ≪1, 其中,μ(c)=(u1(c),v1(c)),σ(τ)=(u2(τ),v2(τ))。另外κ(c*)≠0,又若ξ(τ)≠0(|τ|≪1),则 (7) 那么(u(τ),v(τ))的稳定性由ξ(τ)的符号决定,当ξ(τ)<0时,局部分支解是稳定的,当ξ(τ)>0时,局部分支解是不稳定的。而ξ(τ)和-τc′(τ)κ′(c*)有相同的符号。下面分析c′(τ)和κ′(c*)的符号,从而确定ξ(τ)的符号。 引理3κ′(c*)>0。 证明由L(c,θa,0)μ(c)=κ(c)μ(c)知, 因为κ(c*)=0,由于|c-c*|≪1,所以|κ(c)|≪1,如果v1≡0,那么u1≡0,矛盾,故v1≢0,因此κ(c)是算子 定理6令 若I>0,则局部正分歧解(u(τ),v(τ))是稳定的,若I<0,则局部正分歧解(u(τ),v(τ))是不稳定的。 证明将正分歧解(c(τ),u(τ),v(τ))=(c(τ),θa-τ(ω1+ρ(τ)),τ(χ1+π(τ)))代入模型(2)的第二个式子,两端同除以τ,再关于τ求τ=0处的导数,得 两边同乘以χ1,在(0,l)上积分,并利用格林公式计算得 当I>0时,c′(0)>0,结合(7)式和引理3知,当τ>0时,ξ(τ)<0,从而局部正分歧解稳定。当I<0时,c′(0)<0,类似的分析方法可知ξ(τ)>0,从而局部正分歧解不稳定。 注3若m>a2,则定理6中的I>0,从而局部正分歧解(u(τ),v(τ))是稳定的。 本节利用数值模拟来检验本文所得条件的合理性, 同时进一步定量分析正解的性质。类似于文献[19]取(0,l)=(0,2π),初值条件为(u0(x),v0(x))=(0.5|sinx|,0.1|sinx|),利用常微分方程求解方法计算可得λ1=0.25。其它参数暂定为 m=5,k=2,b=3,d=8。 (8) (ⅰ)平衡态半平凡解存在性 大量的数值模拟结果可总结为:当a=2,c=-2 图2 模型(2)的半平凡解Fig. 2 The semi-trivial solution of model (2) (ⅱ)平衡态正解存在性 大量的数值模拟结果可总结为:当a=2,c=-0.4,1,10,50,其它参数取(8)时,模型(2)存在正解(u,v),见图3(a-d)。当a=8,c=-0.2,1,10,50,其它参数取(8)时,模型(2)存在正解(u,v),见图3(e-h)。 图3 模型(2)的正解Fig. 3 The positive solution of model (2) 上述参数中,c=-0.4>c1≈-0.827 0>c*和c=-0.2>c1≈-0.479 4>c*,这验证了定理4和定理5,同时印证了模型(2)中c取负值是可以产生平衡态正解的。另外,图3(d,h)中u(x)虽然很小,但不是零解。 (ⅲ)食饵防御能力对模型平衡态正解的影响 用平衡态正解在(0,l)上最大值作为范数,记为‖u‖或‖v‖,观察平衡态正解关于参数c的变化情况。大量的数值模拟结果显示,当达到平衡态时,v(x)不会因c变大而无限增大(见图4),a=2(图4(a)),a=8(图4(b)),其它参数取(8)。特别地,图4(b)中,‖v‖依c增大而先增大再减小。 图4 模型(2)正解关于参数c的变化Fig. 4 The change of the positive solution of model (2) with respect to c 以上结果表明,在共存模式下,当捕食者生长率增大,处于平衡态模式中的捕食者不会无限增大,即食饵具有的防御能力可抵御捕食者。另外,从图4可以看出,在适当条件下,当食饵生长率较高时(如a=8),处于共存模式中的捕食者随其生长率增大而出现先增后减的现象,表明高生长率下食饵抵御捕食者的能力更强。 本文主要讨论了一类带有Monod-Haldane型功能反应函数的Variable-Territory捕食模型平衡态正解性质。在一维空间下利用连续延拓技术来克服自控能力项在齐次Dirichlet边界条件下的奇性。利用特征值问题变分原理和分歧理论给出平衡态正解存在的充要条件。运用稳定性理论分析了局部正分歧解的稳定性。最后通过数值模拟验证了平衡态正解的存在性, 同时对平衡态正解关于捕食者生长率的变化情况做了定量分析。结果表明,平衡态共存模式可由食饵与捕食者生长率决定,食饵的防御能力可以有效抵御捕食者。更进一步, 食饵生长率高低影响防御能力的强弱。1 正解存在的必要条件和先验估计








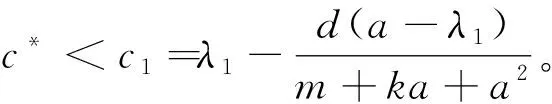




2 正解的局部存在性

g(0)=g(l)=0,g′(0)>0,g′(l)<0。



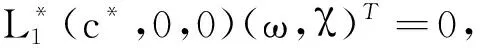



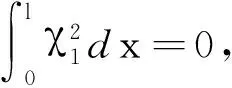
3 正解的全局结构





4 正解的稳定性



5 数值模拟








6 结论

