基于非线性深度递归算法的锅炉模糊自适应控制*

周妮娜

(宝鸡文理学院 电子电气工程学院,陕西 宝鸡 721016)

在研究和分析被控系统时,需要经过模型的构建、分析及设计等几个阶段。实际的受控对象结构日益复杂,如何对具有复杂特征的受控对象开展有效的模型构建,是当前专家学者研究的重点内容之一。锅炉系统具有滞后、非线性等特点,参数之间耦合、关联,系统的实际输出可能并不完全受控于控制器,此时得出的模型参数结果就会出现误差,构建系统模型变得困难。

为了完成对锅炉的有效控制,王朝[1]提出了基于模糊PID理论对集中供热燃气锅炉控制系统进行设计。毛峥[2]提出基于STM32单片机对工业锅炉控制系统进行设计,最大限度地提升系统的可靠性。李丰泽等[3]提出使用模糊自适应PID控制的方法对锅炉燃烧系统进行控制。

本文针对锅炉的非线性特点,提出了一种改进的锅炉模糊自适应控制方法,文中证明了该算法的稳定性,通过结合系统仿真实验,得出了改进型算法的鲁棒性更优、动静态性能更优等结论。

1 锅炉模糊自适应控制方法的相关概念以及计算思路

考虑如下多输入多输出离散系统:

y(k+1)=f(y(k),…,y(k-ny),
u(k),…,u(k-nu))

(1)

其中,u(k)∈Rm,y(k)∈Rn,分别是系统k时刻的输入和输出向量。ny和nu是未知整数。f(·)是一个未知非线性函数,假设f(·)关于u(k)的偏导数连续,且系统(1)满足广义Lipschitz假设,则可以得到定理1。

定理1对满足广义Lipschitz假设且f(·)关于u(k)偏导数连续的非线性系统(1),当‖Δu(k)‖≠0时,一定会存在一个被称为PJM (Pseudo Jacobian Matrix)的时变参数Φc(k)∈Rn×m,使系统(1)转化为如下紧格式动态线性化数据模型(Compact Form Dynamic Linearization,CFDL):

Δy(k+1)=Φc(k)Δu(k)

(2)

其中,Φc(k)∈Rn×m,且

(3)

对任意时刻k,‖Φc(k)‖有界。

基于动态线性化的锅炉模糊自适应控制是运用参数辨识的方法,动态计算PJM时变参数的数值,并在此基础上进行控制的算法设计[4-5]。在现有的方法中,很少考虑了锅炉非线性失控问题。对于实际的物理系统,执行器的执行能力都是有限的,具体体现在控制量的幅度与变化速率的有界性。执行器的执行能力可表示为:

(4)

其中,Δumin,Δumax依次代表了控制量变化速率具有的最大与最小值,uL,uv则依次代表了此时控制幅度具有的最小和最大值。

2 锅炉模糊自适应控制的非线性控制优化方法

本节提出改进的锅炉模糊自适应控制方法,通过分析执行器的执行能力给出控制算法。

2.1 改进的控制器设计

在辨识PJM参数时,采用如下计算方法[6-7]:

(5)

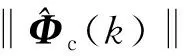
进一步对y(k+1)进行滤波,

(6)

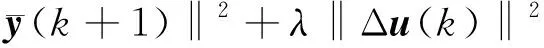
(7)

其中,λ>0为权重因子,可对控制变量的变化幅度进行调整。

设执行器执行能力为:

(8)

则在k时刻控制量增量范围可表示为:

(9)

联立(7)式和(9)式,通过非线性递归方法对其进行求解,可得:

x=-E-1(F+MTx)

(10)

其中,

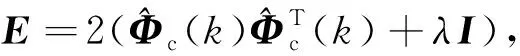
2.2 改进控制算法的闭环稳定性证明

为了对本文所提算法的稳定性进行有效的分析[6],特设定如下假设:

假设1存在这样的λ值,可满足ΦE-1(F+MTx)正定。

假如此时不能够满足假设1的基本条件,则此时说明该算法在非线性失控时,难以有效保障系统的闭环稳定性,则需提高计算的复杂度才行。

通过假设1能够对定理2进行证明。

定理2在非线性系统(1)中,当Δu(k)幅值为有界时,如果此时假设1的条件能够被充分满足,基于文中辨识方案及本文的迭代算法,能够得出,当y*(k+1)=y*=常数时,存在一个正数λmin>0,使得当λ≥λmin时,有:

(2)如果此时的闭环系统是BIBO (Bounded- Input Bounded-output)系统,为稳定的,则此时得到的输出序列{y(k)}和输入序列{u(k)}是有界的。

(11)

则有

(12)

(2)可证明存在λ,使得:

的特征值绝对值均小于1。其中,S(k)是对角矩阵,Si(k)是矩阵S(k)中的第i个对角元素,

(13)

(14)

则进一步有

(15)

(3)证明跟踪误差有界。由(2)知:

(16)

则存在足够小的ε和范数‖·‖,使得

(17)

对任意k取

(18)

(19)

则

(20)

则‖e(k)‖有界,设为f0,即‖e(k)‖≤f0。

(4)由y*(k)有界,能够推导得出此时y(k)为有界的。结合x的求解过程,引入了对控制位置饱和的约束限制,此时的‖u‖是符合当前的约束条件的,能够得出此时的u(k)为有界的。

3 仿真实验

图1 控制性能对比图Fig. 1 Control performance comparison chart

由仿真结果图可以看出,改进的模糊自适应算法响应输入信号速度快,调整时间短,稳态误差小,改进算法的动静态性能较优。

4 结论

本文对锅炉模糊自适应控制中难以有效解决的非线性失控问题展开论述,提出了改进算法,推导过程显示,该算法运算量小,同时对闭环系统中算法的稳定性进行了分析与证明。仿真结果表明该算法具有较好的鲁棒性,对于系统的初始参数不敏感,动态性能好,稳态误差小,较好地解决了锅炉的非线性问题。