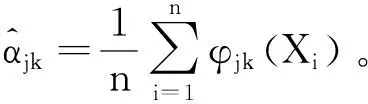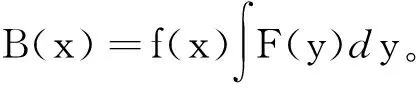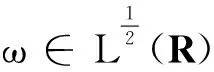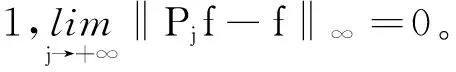负相关随机变量密度小波估计的Lp-相合性*
郝 露,许俊莲
(宝鸡文理学院 数学与信息科学学院,陕西 宝鸡 721013)

1 预备知识
1993年,BOZORGNIA首次提出了负相关随机变量的概念[9]:
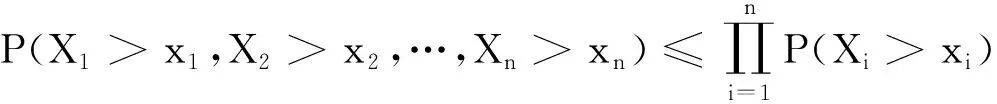
本文将用到下面几个ND样本的相关性质。
性质1[9]设X1,X2,…,Xn是ND随机变量,任给集合{1,2,…,n}的m个两两不相交的子集A1,A2,…,Am以及m个关于每个变元单调非降(非增)函数fi:R#(Ai)→R(1≤i≤m),其中#(Ai)表示集合Ai中元素的个数,则随机变量f1(Xi,i∈A1),f2(Xj,j∈A2),…,fm(Xk,k∈Am)仍然是ND的。
性质2[9]设X,Y是ND随机变量,则
E(XY)≤(EX)(EY)。
性质3[10]设X1,X2,…,Xn是ND随机变量,满足EXi=0和E|Xi|p<∞,则当p≥2时,有
设L2(R)是平方可积函数空间,该空间中的一列线性闭子空间{Vj}j∈Z是其多分辨率分析(Multiresolution Analysis, MRA)指满足[11]:
(ⅰ)单调性:Vj⊆Vj+1,∀j∈Z;
(ⅲ)伸缩性:f(x)∈V0⟺f(2jx)∈Vj,∀j∈Z;
(ⅳ)基的存在性:存在φ∈L2(R),使得{φ(x-k)}k∈Z为V0的标准正交基,其中φ称为该MRA对应的尺度函数。

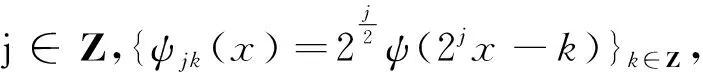
(1)
其中,αJk=〈f,φJk〉,βjk=〈f,ψjk〉。
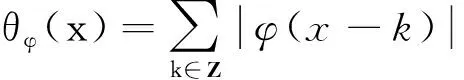
注意到,φ满足(θ)条件蕴含φ∈L1(R)∩L∞(R),从而φ∈Lp(R),1≤p≤∞。正交小波基的重要性在于它不仅是L2(R)中的标准正交基,而且在一定条件下也是Lp(R)(1 记Pj为L2(R)到尺度空间Vj上的正交投影算子,则对于f∈L2(R)及αjk=〈f,φjk〉,有 (2) 对于f∈Lp(R)也有类似于(1)式的展式。进一步当尺度函数φ满足(θ)条件时,(2)式仍然成立。 S条件可推出(θ)条件(见文献[12]引理8.5)。由文献[12]可知,在S条件下,有以下结论成立: 引理1设尺度函数φ满足S条件,则对f∈Lp(R)(1≤p<∞), 其中,Pj为尺度空间Vj上的正交投影算子。当函数f一致连续时,上式对p=∞仍然成立。 |K(x,y)|≤F(x-y)。 (3) (4) 在本文中,AB表示A≤CB,其中C为独立于变量A和B的正常数;AB等价于BA;用A~B表示AB和BA同时成立。 证明根据范数的三角不等式性质, 为了得到相应的结论只需说明 (5) 下面根据p的取值情况分3种情形说明: (1)当p=1时,显然 (6) 以及 可得, 因为尺度函数φ满足S条件,根据引理2,有 |Kj(x,y)|≤2jF(2j(x-y))。 代入上式,经过简单变换可得: (7) 其中, (8) 另一方面,记Yi=Kj(x,Xi),则 因为选取的尺度函数φ是单调的,所以核函数K关于每个变元也是单调的。根据性质1可得随机变量Y1,Y2,…,Yn仍然是ND的。再由性质2有 利用Jensen不等式, (9) 其中, 结合(7)式和(9)式, (10) 另一方面, min[B(x),Cn(x)]≤B(x)∈L(R)。 因此,由Lebesgue控制收敛定理可得 结合(8)式,(10)式和(6)式,(5)式成立。 (2)当p≥2时,由(4)式可知: 记Zi=Kj(x,Xi)-Pjf(x),则上式简化为 (11) 经过计算可得, 故EZi=EKj(x,Xi)-Pjf(x)=0。根据φ的选取以及性质1推出随机变量Z1,Z2,…,Zn仍然是ND的。由于|Pjf(x)|p=|EKj(x,Xi)|p≤E|Kj(x,Xi)|p,故 E|Zi|pE|Kj(x,Xi)|p= (12) 利用性质3及Jensen不等式可知 代入(11)式可得: (13) 又因为 而F∈L1(R)∩L∞(R)可推出F∈Lp(R)(1 综合(13)式可得: (3)当1 由情形(1),(2)可知,(5)式在1 综上可得,对于1≤p<∞,都有 证毕。 下面给出p=∞时的相合性。 证明根据范数不等式, (14) 由(3)式可得, 再根据φ的有界性, (15) 由于Eφjk(Xi)=αjk,利用Jensen不等式及性质2,可知 (16) 又有 结合(15)式和(16)式,得 (17) 显然 (18) (19) 根据已知条件f(x)≤ω(|x|),可得 (20) 将(20)式和(19)式代入(18)式,再结合(17)式有
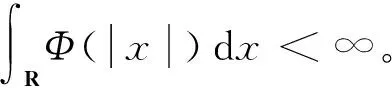

2 主要结论