高速有质量偏心的轴承-转子系统瞬态热效应的研究

富彦丽

（上海应用技术大学 机械工程学院, 上海 200235）

轴承-转子系统的运行稳定性问题一直是转子动力学研究的重要课题之一。20 世纪90 年代，学者们应用非线性转子动力学法研究轴承-转子系统的稳定性[1-3]，这种方法可以解释各种非线性现象，但是不能把复杂的温度变化考虑在计算模型内，因而得到的轴心轨迹与实际有着差别。到了21 世纪，各种计算机辅助工程(computer aided engineering，CAE)分析软件开始出现，并开始应用在轴承-转子系统的稳定性分析中[4-8]，但其也未能准确模拟真实工况下的轴承-转子系统的运行情况。随着计算机技术的继续发展，仿真法开始应用于轴承-转子系统的稳定性研究中[9-10]，仿真法虽然不能对非线性现象做出物理解释，但是能够将温度和压力对润滑油黏度的影响、轴瓦和轴的热变形及受力变形等因素考虑在内，精确地模拟分析转子的轴心轨迹，而且能够考察这些因素对转子轴心轨迹的影响，为工程实际中的轴承-转子系统设计提供相对准确的理论支撑。

本文将用仿真法研究在考虑油膜三维瞬态温度场和轴瓦三维瞬态热传导的情况下有质量偏心的转子运动情况，并和只考虑二维绝热温度场的结果相比较，来说明考虑更全面的因素，建立更全面数学模型的必要性。随着转速的提高，对仿真算法收敛稳定性的要求也提高，在高速下考虑这么全面的因素分析轴承-转子系统稳定性十分困难，本文通过改进Newton-Raphson 算法同时求解雷诺方程和运动方程，来解决高转速下仿真算法难收敛的问题。

1 数学模型的建立

油膜厚度分布方程、三维瞬态油膜能量方程、三维瞬态轴瓦热传导方程、润滑油的黏度和密度随着温度和油膜压力变化方程等都与文献[10]相同，本文着重介绍改进Newton-Raphson 算法用到的方程，即三维瞬态Reynolds 方程和有质量偏心的转子的非线性运动方程。

式中：R、h0分别为轴承半径和半径间隙；η0、ρ0分别为进油温度和压力下的动力黏度和密度；U为轴颈旋转线速度；u0是为了便于编程和对结果讨论而取的速度虚拟参考量；p为油膜压强。且：

其中：

分析转子的受力情况知，转子在油膜压力、质量偏心力和外载荷作用下有如下的运动方程。沿垂直方向和水平方向分别为：

式中：R为轴承半径；L为轴承的宽度；θin、θout分别为进油和出油边；W为载荷，M为转子的等效质量；ub为质量偏心距；U为轴颈旋转线速度。

治疗后，观察组患者的治疗总有效率明显高于对照组患者，差异有统计学意义（χ2=8.4，P＜0.05），见表 2。

这样，有质量偏心的转子系统的瞬态问题与文献[10]研究的瞬态问题的区别，就是用式（4）和式（5）分别代替文献[10]的沿水平和垂直方向的运动方程式；温度场的求解方法与文献[10]也完全相同。压力场和轴心运动轨迹的求解将使用改进的Newton-Raphson 算法[11]。

2 数值方法

Reynolds 方程的离散和边界条件见文献[9]。

将时间离散，在每一时刻，用Newton-Raphson法同时求解轴颈的运动方程和三维瞬态Reynold方程，得到轴心的沿2 个方向的运动速度及动压油膜的压力分布，通过对速度的数值积分和微分得到轴心下一时刻沿2 个方向的位移和运动的加速度。

定义式（1）的左边为P1，右边为P2，则在节点（k，l）处方程可改写为：

用W y代替式（4）的右端，则：

于是得到如下Jacobi 矩阵：

其中方括号内是方阵，大括号内是列矩阵。上面的矩阵简写为：

得到轴心运动的速度后，则2 个方向的运动加速度为：

下一时刻轴心位置为上一时刻的位置加上新的位移：

计算表明改进Newton-Raphson 法用于求解三维瞬态雷诺方程和油膜运动方程在高速下也有很好的收敛性。

计算程序的流程示意图如图1 所示。

图1 程序流程示意图Fig.1 Program flow diagram

3 有质量偏心的转子—轴承系统瞬态性能的分析

程序输入的原始数据与文献[9]相同。

图2 是考虑二维绝热温度场时转子圆周速度为40m/s 时在受到不同的质量偏心力后的轴心运动轨迹。可以看到，几种偏心率的情况下，轴承都由于轴心轨迹范围太大而失效，没有形成最后的极限环轨迹。其原因是轴承发生了热不稳定造成的，从图3 可以看到在轴承失效之前，温度有一个突然上升的过程，在轴承失效时，轴承中的最高温度已经接近140 ℃。计算还发现，继续增大质量偏心率，轴承都会发生温度突然上升而导致失稳现象。这种现象与考虑的温度模型有关，只考虑了油膜的二维温度场，没有考虑轴瓦的导热，因而过高估了油膜的温度。

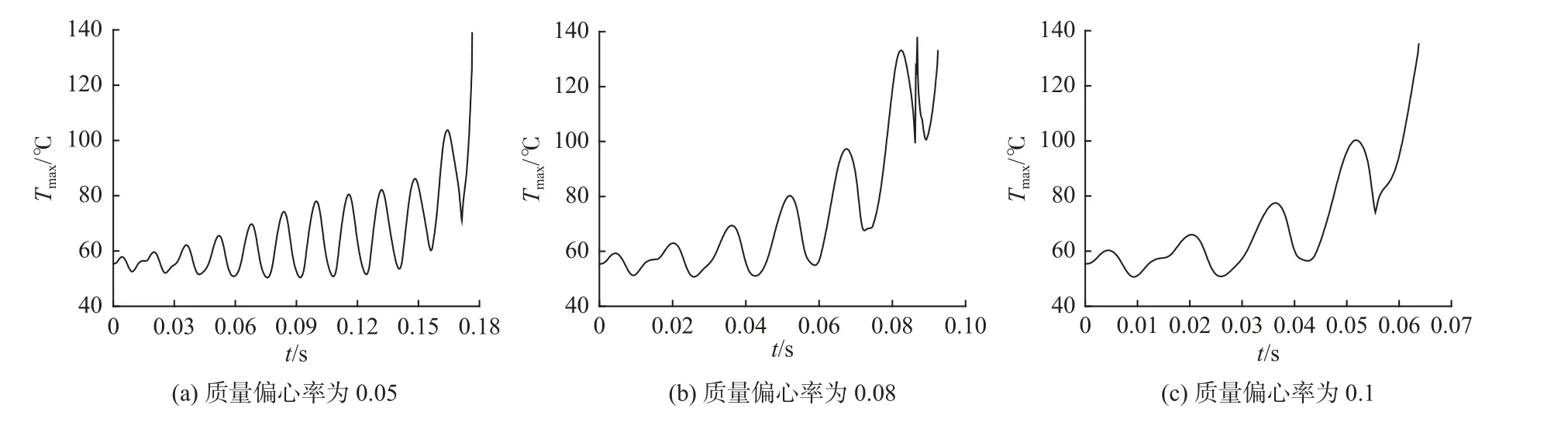
图3 考虑二维绝热温度场时的最高温度响应Fig.3 The maximum temperature response considering two-dimensional temperature

图4 是考虑轴承的三维温度场圆周速度为40 m/s 时在受到不同的质量偏心力后的轴心运动轨迹。经过计算发现，在质量偏心率低于0.19 时轴心经过涡动发散，最后停留在一个极限环上运动，如图4（a）和（b）所示；超过0.19 以后轴心轨迹开始有旋涡出现，说明轴系发生了分岔，并且随着质量偏心率的增大旋涡越来越大，如图4（c）～（e）所示；当质量偏心率超过一定值以后轴心轨迹又恢复到最终在一个极限环上运动，如图4（f）所示。由图4 可知，在某些情况下，随着质量偏心率的增大，轴心轨迹范围反而变小，这说明在考虑三维温度变化时，质量偏心力在某些工况下也会有增稳的作用。在速度为40 m/s 并考虑轴承的三维温度场时，轴承没有失效现象发生，其原因是此时的温度没有升高到发生热不稳定现象，如图5 所示。

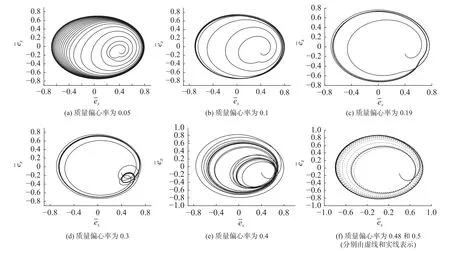
图4 考虑三维温度场时的轴心轨迹Fig.4 The moving trail of the axis considering three-dimensional temperature

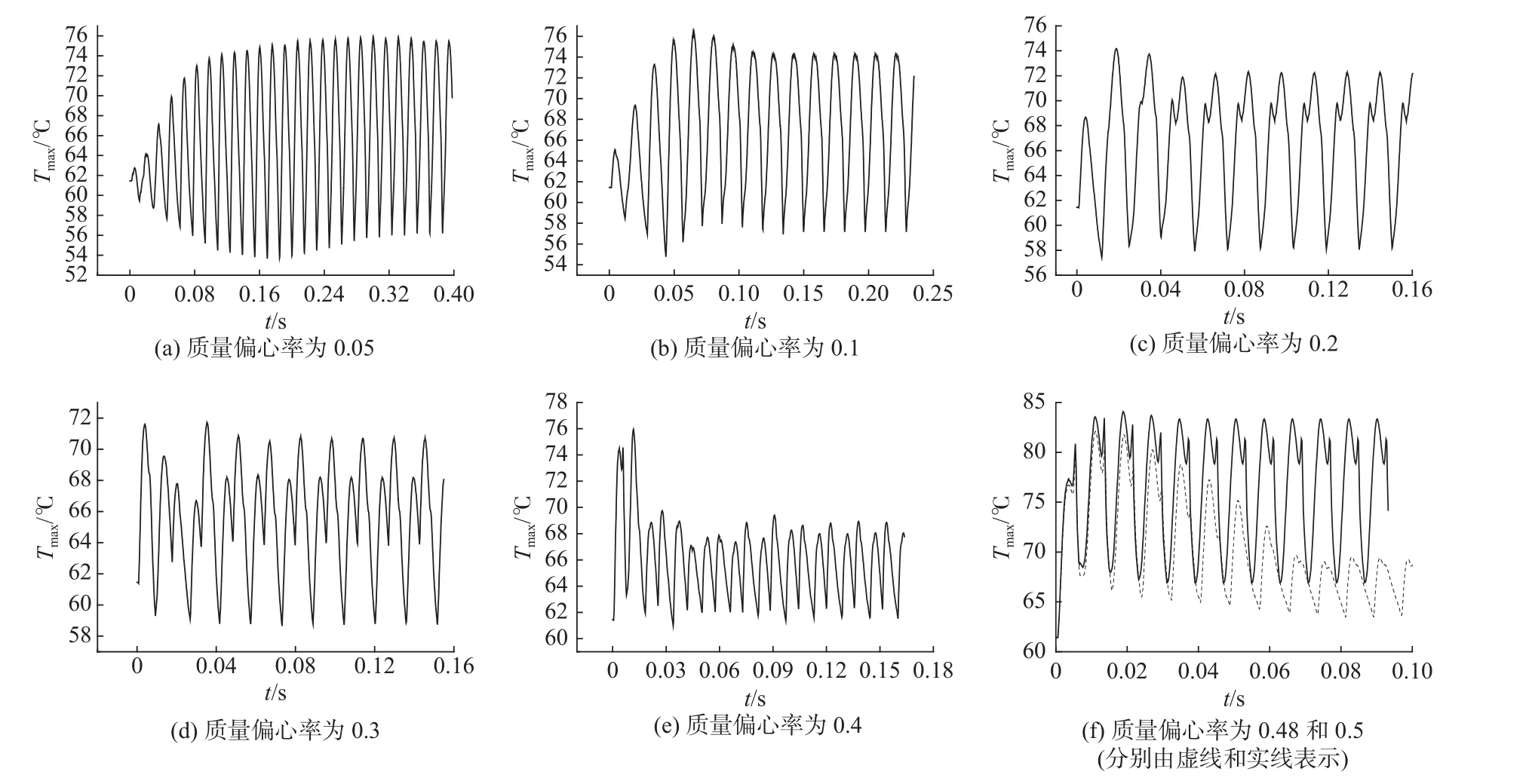
图5 考虑三维温度场时的最高温度变化Fig.5 The maximum temperature response considering three-dimensional temperature

图5 是在同样的速度下考虑三维温度变化时轴承的最高温度在受到质量偏心力后的响应过程。可以看到，在轴承没有失效之前，温度响应在轴心轨迹达到极限环后也稳定在恒定的振幅上振动，质量偏心率为0.05 时的振幅为20 ℃左右；质量偏心率为0.1 时的振幅为18 ℃左右；虽然质量偏心率增大最终温度响应的振幅降低，但是质量偏心率为0.1 时温度响应过程中的最高值要稍稍高于不平衡偏心率为0.05 时的情况，前者为76.5 ℃，后者为75.8 ℃。在轴心运动轨迹出现旋涡以后，温度也以相应的方式做周期响应，质量偏心率为0.3 时在响应过程中的温度最高值最低，而质量偏心率为0.4时最终温度响应的振幅最小，质量偏心率为0.5 时最高温度值最高；质量偏心率为0.48 和0.5 时，最终轴心轨迹都停留在一个极限环上，最终温度振荡的周期也相同，只是质量偏心率为0.5 的振幅要高于0.48 时的振幅；温度响应过程之所以如此复杂，归根结底是由决定温度的能量方程决定的，能量方程本身是一个非线性分布参数系统决定了温度的非线性特性。

比较图2 和图4 可以看到，在圆周速度为40 m/s 时轴承受到不平衡质量偏心力后，考虑2 种温度模型得到的轴心运动情况有很大的差异。通过上面的分析，对于有质量偏心存在的轴承-转子系统，轴承的热不稳定性使轴承容易发生失效现象，考虑二维绝热温度会过高地估计轴承的温度和热不稳定性，从而得到的轴承性能与实际存在着很大的差异，因而要得到相对准确的轴承性能必须考虑轴承的三维瞬态温度场。

4 结 语

通过改进Newton-Raphson 算法，将轴瓦的三维热传导和油膜的瞬态三维温度场考虑在内得到高转速下转子轴心的运动轨迹。只考虑油膜的二维绝热温度场会过高估计轴承的温度和热不稳定性；油膜三维瞬态能量方程的非线性导致温度响应的复杂性。对于高转速的轴承转子系统，在全面考虑温度影响时可以发现质量偏心有一定的增稳作用。