由一道题的典型错解引发的教学思考
达娃央宗
摘要:文章通过对2022年西藏自治区初中学业水平考试中一道统计与概率题的答卷分析,整理学生用列表法或树状图求概率时出现的典型错解,深入剖析典型错解背后的原因,结合发展学生数学核心素养对教学提出四点思考和建议.
关键词:错解分析;核心素养;教学建议
笔者在2022年西藏自治区初中学业水平考试阅卷中发现,不少学生用列举法求概率时书写不规范,暴露出部分学生推理能力、运算能力及数据观念等数学核心素养不足的问题,笔者试对学生答题情况进行分析.
1 试题及简析
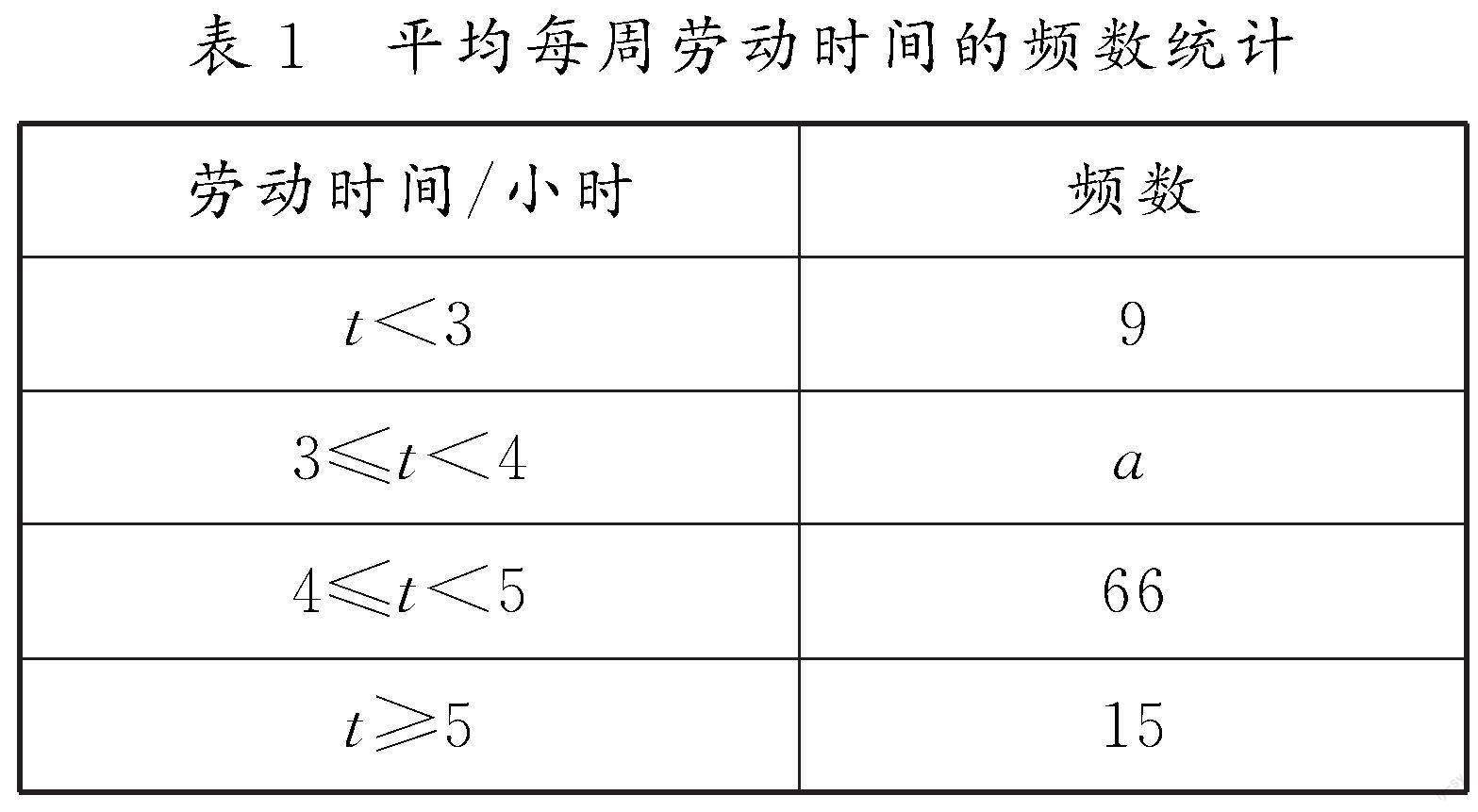
试题 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如表1和图1.
请根据图表信息,回答下列问题.
(1)参加此次调查的总人数是[CD#3]人,频数统计表中a=[CD#3];
(2)在扇形统计图中,D组所在扇形的圆心角度数是[CD#3]°;
(3)该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.
试题第(1)(2)问的解答略.对于第(3)问,可用列表法列出所有可能的结果,如表2所示.
用画树状图的方法列出所有可能的结果,如图2所示.
由表2或树状图可以看出,所有可能出现的结果共12种,这些结果出现的可能性相等,其中恰好抽到一男一女的结果有8种,所以
2 答题错解及分析
阅卷时发现本题第(3)问的答案无奇不有,每一步都有典型的错解.
2.1 列表时的三种典型错解
(1)不标记序号.如表3,对不同的男女没有用男1、男2、女1、女2来标记.出现这种错误是因为不理解“等可能事件”的意义,并且没有在日常教学中养成规范书写等可能事件的习惯.
(2)不能区分“放回”与“不放回”.如表4,答题时对“放回”与“不放回”混淆不清.其原因是不理解具体的“事件”,逻辑不严谨,或者审题不仔细等.
(3)列表不规范.有学生直接用列表法把几种情况列出来(如表5),其原因是没有掌握正确的列表方法.
2.2 画树状图时的三种典型错解
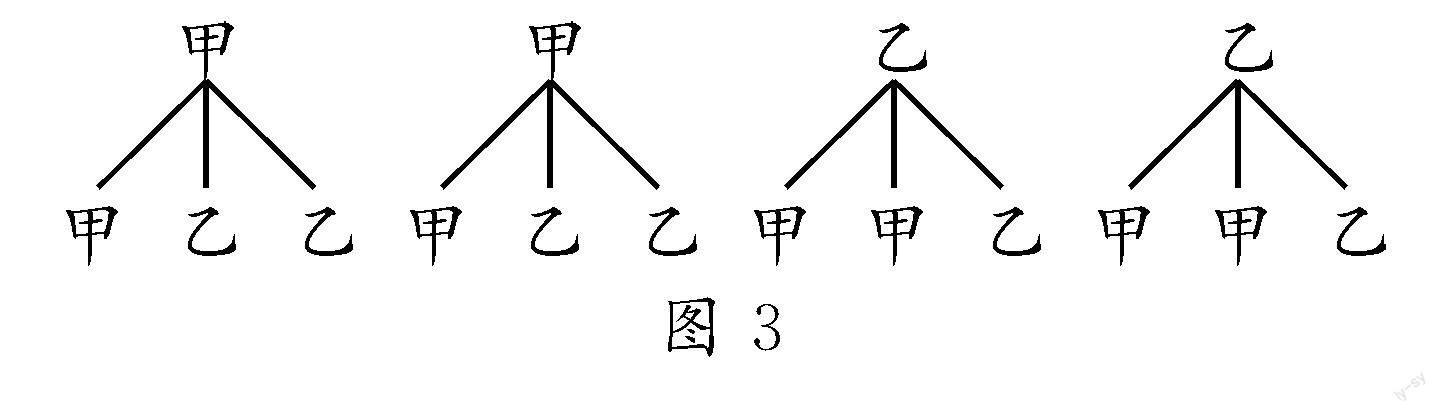
(1)不做序号标记.如图3,甲是男还是女,如果表示男,是男1还是男2,均未明确标注,这种表述不清晰、书写不规范的问题,说明学生缺乏“用数学语言表达世界”的素养,缺乏用数学语言准确表达并传递信息的能力.
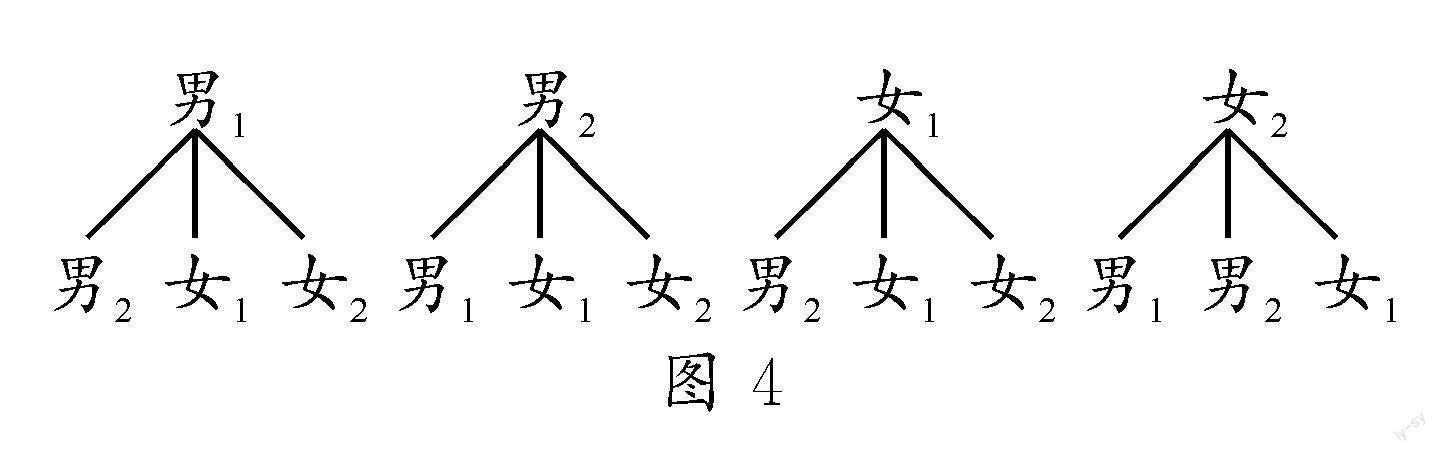
(2)重写或漏写.如图4,有考生画树状图时出现重写,这反映出部分学生没有养成良好的解题习惯,解题不专注、不细心.
(3)不会画树状图.还有一些学生在画树状图时出现了图5中的情况,说明这部分学生没有理解等可能事件的意义,没有理解树状图的意义,因此不会画树状图.
2.3 求结果时的三种典型错解
分析上述三类九种错解可以发现,学生出现错解主要有三个方面的原因:
(1)没有掌握概率相关知识
不能区分“放回”与“不放回”,未能掌握列表和画树状图的正确方法,不能准确理解树状图表示的结果.
(2)没有养成良好的数学解题习惯
分析发现,几乎每一种错解中都出现了审题不仔细、书写不规范、解题不专注等情况.
(3)基本计算能力有待提高
计算出现不约分、约分错误、约分与开方混淆等情况.
3 基于典型错解的教学建议
根据上述典型错解及原因分析,笔者提出以下四个方面的教学建议.
3.1 根据课程标准提高教学要求
2019年以前,概率题在西藏中考中常以选择题的形式出现,考查“一步概率”,分值3分.自2019年起,概率题出现在主观题中,“一步概率”向“两步概率”转型.2020年-2022年在解答题中考查用列表法或树状图求“两步概率”,分值4~5分,近五年概率在西藏中考中的考查情况见表6.
《义务教育数学课程标准(2022年版)》对概率提出如下要求:能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定随机事件发生的所有可能结果,了解随机事件的概率[1].因此,教师在教学中要立足课本与课程标准,明确教学目标、中考考点,提高教学要求,多解题,多分析,多总结,引导学生解决知识点掌握不牢的问题.
3.2 改善教学形式以落实教学目标
帮助学生理解“等可能事件”,帮助学生厘清“放回”与“不放回”,帮助学生理解列举法并正确列表或画树状图,这些教学目标要落实好,建议基于“至简数学”理念[2]充分设计,通过“改善学”“改善教”落实教学目标[3].
在课堂教学中有效落实教学目标,需要以教学活动为载体,通过积极的活动、体验和感受持久地引导学生逐步实现.因此,课堂教学需打破固有的模式,改善教学的形式与内容,将数学知识融入活动中,让学生在“做中学”“学中做”,努力变纯粹的数学教学为丰富的数学活动.比如,让学生做石头剪刀布的游戏等.教学中把数学问题与实际生活结合起来,把问题放进相应的实际背景中,巧妙地设计动手操作实验,放手给学生时间并創造条件让学生经历解题的整个过程,尤其是解题之后的反思,让学生通过大量的实验活动来感悟、体会,绝不能直接将结论告诉学生.
学生只有通过自身积极主动地参与活动,才能获得体验.教师必须通过适当的教学预设,引导学生积极体验数学学习过程中的直觉、抽象和数学美等,而不是直接把自己的体验灌输给学生.
3.3 培养学生的数学学习习惯
初三下学期一位数学教师在一个实验班做了一项“消除六害”的实验.所谓“六害”,是指“看错(题目中的条件)、抄错(题目条件或解答过程中的符号或数字)、笔误、答错位置、漏写单位、漏写步骤”.一个月后,通过与对比班比较,发现学生的数学平均成绩提高了7分.这样的成绩引起了同事的兴趣.另一位教师从初一开始就注意培养学生良好的数学学习习惯,结果他班上的学生,无论是数学成绩还是数学书写、数学表达等基本素养,都明显高于其他班级.这项实验虽然只是个案,但足以说明培养学生良好数学学习习惯的重要性和其对提高学生数学素养的广泛影响力.
求两步概率,若题干中有“放回”或“不放回”的字眼,学生往往能够分辨,难就难在没有出现明显的字眼时,学生就容易混淆“放回型”和“不放回型”,归根到底问题出在学生的审题能力上.良好的审题能力是解决问题的前提,解题时不仅要读懂字面上的含义,还要透过文字发掘其背后隐含的信息,这就需要学生有较好的阅读理解能力.因此,作为数学教师,要格外注重提高学生的审题能力.
3.4 培养学生运算能力
学生计算能力不足在该题中再一次凸显出来,因此培养学生数学运算能力迫在眉睫.
考试中学生常因计算失误丢分,教师为此也下了不少苦功.我区学生数学基础相对薄弱,更应注重学生数学运算能力的培养.笔者做了一个实验,每节课利用前5分钟,设置3至5道基础计算题小测,一个原本在年级7个班里均分垫底的班级,经过一个学期的训练后,均分提升了近10分,跃居全年级均分第二名.由此可见,计算能力的训练对于基础薄弱的学生来说影响是显著的.因此,笔者认为数学运算素养的培养要常抓不懈.
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022.
[2]邓凯,张青.由一节公开课管窥“至简数学”的基本理念[J].中学数学,2021(10):10-13.
[3]邓凯.“至简数学”教学设计的基本框架[J].中学数学,2023(6):7-9.

