基于自适应扰动观测器的PMSM模型预测电流控制

金爱娟，张劲松，李少龙

基于自适应扰动观测器的PMSM模型预测电流控制

金爱娟，张劲松，李少龙

（上海理工大学，上海 200093）

为了实现包装自动化生产线的高性能控制，针对永磁同步包装驱动电机在模型预测电流控制中对扰动敏感性较大的问题，设计一种基于自适应扰动观测器的模型预测电流控制策略。利用预测误差设计一种自适应扰动观测器，对系统遭受的内部和外部的不确定扰动，扰动观测器估计总扰动并以电流的形式进行补偿。将系统的瞬态过程和稳态过程分别进行考虑，设计一种含有动态权重因子的新型损失函数。通过MATLAB/SIMULINK仿真表明，与传统的控制方法相比，文中方法可以保持瞬态下的高速动态响应和稳态下的低电流纹波，并在应对参数失配和负载突变等问题上，展现了更好的稳态性能和抗干扰能力。文中方法可以有效提升系统动态性能和鲁棒性，使改进后系统更加适用于包装机的应用场景。

永磁同步电机；自适应方法；扰动观测器；动态权重因子

未来五年是全面建设社会主义现代化国家开局起步的关键时期，包装印刷业也正在走向高质量发展的重要转型阶段。包装驱动电机作为包装生产传动装置中的核心驱动设备，如何有效地优化其性能指标，成为包装行业迈向高质量发展阶段的重要突破口。永磁同步电机（PMSM）凭借其功率密度大、效率高、控制性能好等优点[1]，使其作为驱动设备被广泛应用于自动化包装生产线，例如输送带、旋转器和封口机等，其性能指标很大程度上影响着生产效率以及产品质量。近年来，随着微处理器的快速发展，有限集模型预测控制成为PMSM驱动系统最有前途的控制技术之一，因为其无须调制技术的辅助，具有更快的动态响应能力，可以有效地处理多目标协调和非线性目标[2]。一般来说，模型预测转矩控制（MPTC）[3]和模型预测电流控制（MPCC）[4-5]是2种常见的MPC形式。由于转矩的测量在实际包装生产过程中存在一定难度，所以本文采用适用范围更广的MPCC方案。然而驱动电机的MPCC控制策略高度依赖于模型参数，并且在应对外部扰动时的控制效果往往比较欠佳，但在实际包装生产过程中，环境温度或湿度的变化以及电机内部结构磨损老化，都会造成电机内部固定参数的改变。同时，包装驱动电机的外部扰动主要来自于电网电压的波动以及包装生产线中负载变化，例如在液体产品的自动化包装生产线中，在灌装的过程中其负载会发生改变，并且其变化是极其快速的。因此需要通过采取相应的改进方案来应对包装过程中的负载突变，以确保生产线的稳定运行和产品质量的稳定性。为了使MPCC控制策略更加有效地应用于包装驱动电机，如何在充分保持MPCC高速动态特性优势的同时，提高其应对扰动时的鲁棒性成为优化驱动电机性能指标的重要研究方向。

为了解决上述不利因素带来的影响，国内外涌现了大量的方法，其中，比较经典的一种策略是通过建立扰动观测器[6-9]来提高MPCC应对扰动时的鲁棒性。随着控制理论的发展，扰动观测器的形式也变得多样，例如有Luenberger扰动观测器[7]、滑模扰动观测器[8]和扩展状态观测器[9]等。Mohamed等[10-11]提出了一种具有自适应内部模型的控制方案，利用Lyapunov函数推导出自适应律，通过内部模型的输出与实际输出之间误差的积分来进行干扰估计。王立俊等[12]将自适应内模观测器引入MPCC系统，用于估计系统扰动并实时补偿，但其自适应增益都为固定值。本文根据预测误差值设计了自适应可变增益，以尽可能减少参数失配对扰动估计的准确度带来的不良影响。

此外，针对MPCC方法中的损失函数，许多学者的研究都集中于采用智能算法对损失函数中的权重因子进行在线寻优，例如模糊方法[13]、粒子群优化算法[14]和神经网络算法[15]等，以提高系统自适应调节能力。其忽略了对损失函数本身的探究，Liu等[16]提出了一种具有比例积分形式的损失函数策略，可以有效消除系统产生的稳态误差。但是积分环节的引入，必然会对系统的响应时间造成影响，尤其是瞬态过程的响应时间。为了有效克服这一问题，本文针对系统不同的运动状态，设计不同的损失函数，并通过速度误差函数使其在不同状态之间实现平滑过渡。

通过对上述文献研究分析，为了有效提高包装驱动电机MPCC系统的鲁棒性，提出一种含有可变自适应增益的扰动观测器，利用预测误差估计系统总扰动并进行前馈补偿以校正输出。针对系统不同的运行状态，本文设计一种含有动态权重因子的损失函数，将系统瞬态过程和稳态过程分别进行考虑，既要保持瞬态中的快速动态响应，还要保证稳态下的低电流纹波。通过仿真实验表明，本文提出的复合型MPCC方案较传统的MPCC系统具有更强的鲁棒性和稳态响应性能。

1 传统MPCC算法

1.1 含有扰动项的PMSM数学模型

为了便于控制器的设计，忽略铁芯的铁损和磁体涡流损耗等因素，在同步旋转坐标系（轴）建立含有集成扰动项的表贴式PMSM数学模型为：

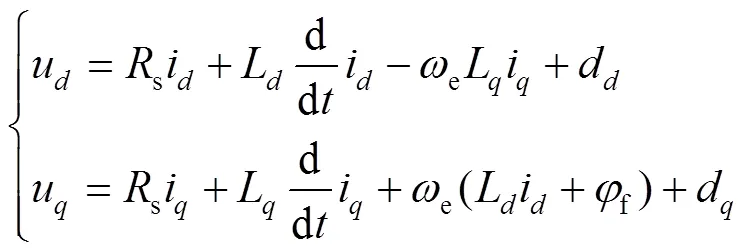
式中：u、u分别为轴定子电压；i、i分别为轴定子电流；L、L分别为轴的定子电感，对于表贴式PMSM定子电感满足L=L=Ls；s为定子电阻；e为转子的电角速度；f为永磁体磁链；d、d为由参数不匹配和未建模动力学模型引起的总扰动，可以由式（2）表示。

式中：ε、ε为模型中的不确定参数项；st−s，∆L=Lst−s，fft−f，ststft为实际参数值，ssf为标称参数值。

对于离散时间模型，下一个时刻的电流i(1)(,)预测模型表示如下：

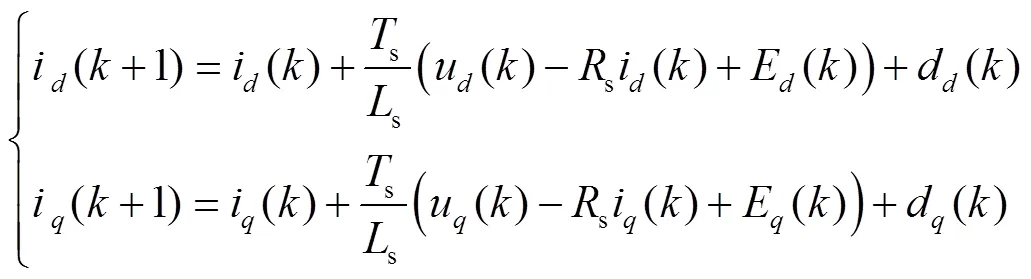
式中：E()e()si()、E()e()si()−e()f分别为轴反电动势在时刻的值；u()和u()分别为-轴电压在时刻的值；i()和i()分别为-轴电流在时刻的值；s为采样周期；i(1)和i(1)分别为-轴电流在下一个采样时刻的预测值。

1.2 PMSM两电平电压源逆变器电流控制方案

MPCC选择电流作为控制变量，通过损失函数筛选出最优电压矢量使预测电流值尽可能地跟踪参考电流值。以两电平电压源逆变器（2L-VSI）为例，其8种开关状态组合产生8个电压空间向量组合，包括6个非零向量和2个零向量，将其映射到复平面得到电压空间矢量，见图1。

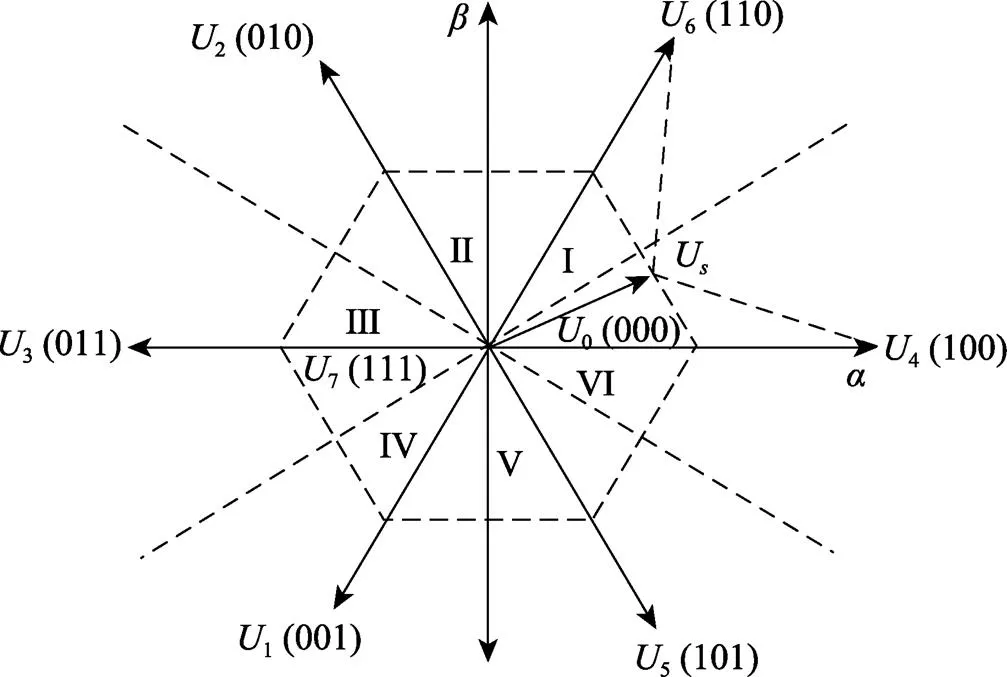
图1 2L-VSI电压空间矢量图

在获得预测值后，通过式（4）中的损失函数来确定最佳电压矢量，最终得到传统MPCC的结构如图2所示。

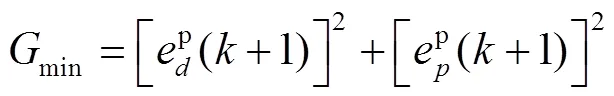
2 自适应扰动观测器

通常认为在MPCC系统中面对的主要扰动是由参数不匹配、未建动力学模型以及突然变载而产生的，其可以被认为是总扰动，利用扰动观测器估计并结合前馈补偿从而有效地消除电流静态误差。

2.1 扰动观测器的建立

本文扰动观测器的建立引用Mohamed等[11]提出的内部模型。为了便于推导扰动估计的自适应律，将式（1）的系统方程重新描述为式（5）。

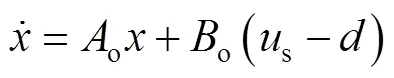
根据式（5）建立系统状态估计方程为：

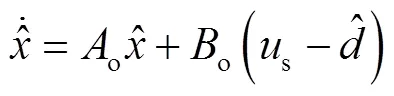
用式（5）减去式（6），得到系统实际采样电流和预测电流之间的误差方程为：

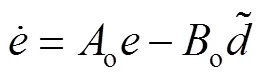
为确保状态预测误差和扰动估计误差收敛为0，建立Lyapunov函数为：

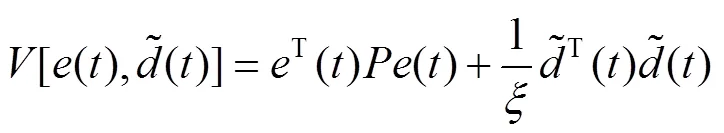
式中：为需要设计的自适应增益；为Lyapunov方程的唯一对称正定解，表示见式（9）。

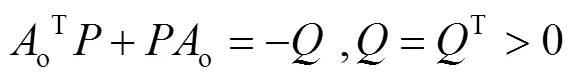
求对时间的导数，并将式（7）带入化简得到：

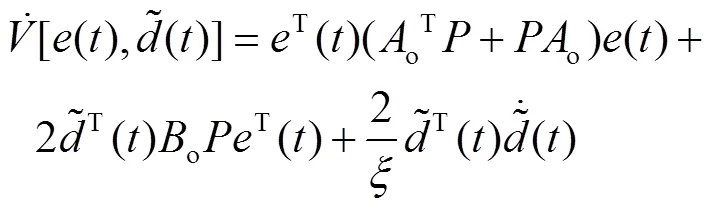
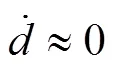
图2 传统MPCC结构

Fig.2 Traditional MPCC structure

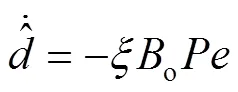
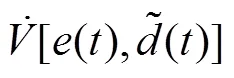
针对本文所适用离散控制系统，式（11）的离散形式表示为：

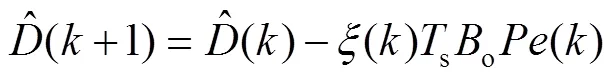
2.2 可变自适应增益的设计

通过分析式（12）可知，若要得到估计扰动，需要准确的电感参数值。实际上，由于磁饱和现象，会产生电感失配的现象。为了缓解这一问题，使其估计值在任何状态下都能够快速收敛，在离散状态下对自适应增益()进行设计。

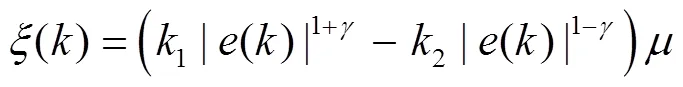
其中，1＞0，2＞0是所需要设计的常系数，0＜＜1是所需要设计的幂指数，＞0为固定扰动估计增益。

对其分析可知，如果估计误差的绝对值足够大时，表示系统内部可能发生参数失配或者受到强烈的外部干扰，此时1||1+γ起主导作用，2||1−γ其值接近于零，利用幂函数型增长的快速性使扰动估计值快速收敛。当估计误差的绝对值足够小时，仅使用1||1+γ时函数存在局限性，需要通过2||1-γ来平衡配置，使系统在估计误差较小时也可以快速收敛。随着系统进入稳态，估计误差减少到零时，此时()=0，扰动观测器不再估计扰动，并补偿电流进入前向通道，系统随之平稳运行。

2.3 系统稳定性分析

本节提出的自适应方法需要选择适当的自适应增益，以保证系统的稳定性。因为MPCC为离散控制系统，所以在离散状态下定义Lyapunov函数为：

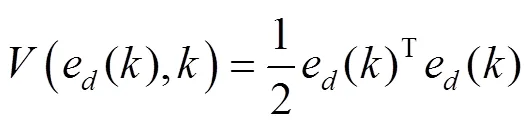
对求离散状态的导数，并化简得到收敛条件必须满足为：

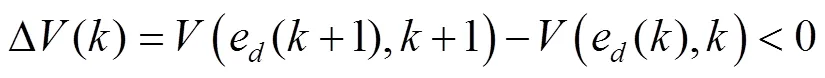
结合式（5）、式（6）以及式（12），可以得到：

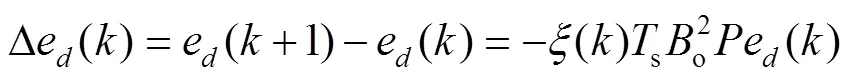
将式（16）代入式（15）得到：

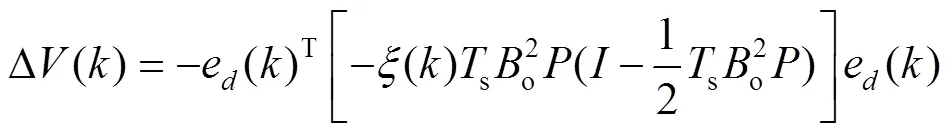
为了满足稳定性的条件，得到自适应增益()的取值范围为：

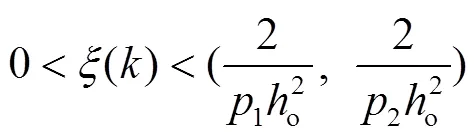
式中：P=diag(p1, p2)；ho=Ts/Ls，与采样周期和定子电感有关。所设计的自适应扰动观测器可以根据电流预测误差进行在线补偿，并且结构简易，更容易在离散控制系统中实现，其结构如图3所示。

3 基于动态权重因子的新型损失函数

传统模型预测电流控制的损失函数计算简易，但针对不同的应用场景，需要选择合理的控制目标。为了保持瞬态中的快速动态响应和稳态下的低电流纹波，对瞬态过程和稳态过程分别进行考虑，以产生2种不同的轴电流基准，一种作为瞬态基准以保持快速动态响应，另一种作为稳态基准以确保低电流纹波。并且，将上一小节的扰动估计值结合到损失函数内，本文提出了一种含有动态权重因子的新型损失函数。

3.1 瞬态q轴电流损失函数

为了保持MPCC瞬态过程具有快速动态响应的优点，继续沿用传统MPCC的参考电流策略，利用PI控制器根据速度误差生成参考电流i*，同时，将上一节求得的扰动估计值前馈补偿到参考电流，则瞬态轴电流损失函数定义为以下形式：

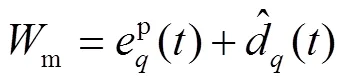
由于MPCC通过离散形式实现，因此，将式（19）进行离散化处理如下：

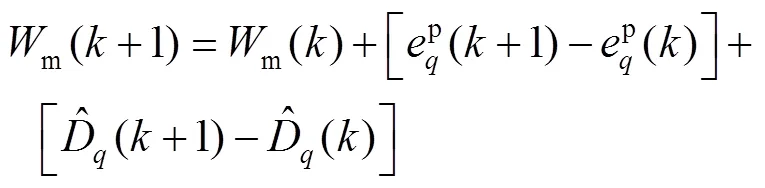
3.2 稳态q轴电流损失函数

由于p是由短期预测产生的，若持续使用其预测值，则无法解决稳态下的电流纹波问题。为了提高稳态时电流控制性能，增强系统应对扰动时的鲁棒性，引入电流跟踪误差的积分环节，将损失函数设计为PI形式，其表达式为：

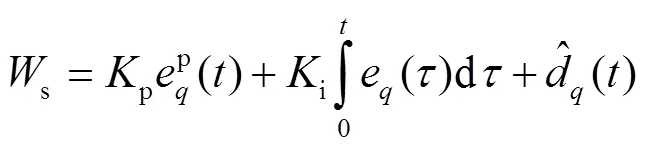
同样，将式（21）进行离散化如下：

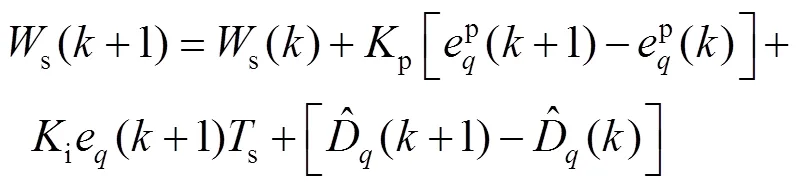
因为集成扰动的信息包含在电流跟踪误差中，通过引入积分作用可以有效消除稳态电流跟踪误差，减少电压矢量切换次数，从而降低稳态时电流纹波。并且，由于积分作用的存在，还可以降低高频采样下量化噪声的产生的负面影响。

将上述2种状态有机结合，所设计的新型损失函数表示为式（23）的形式。

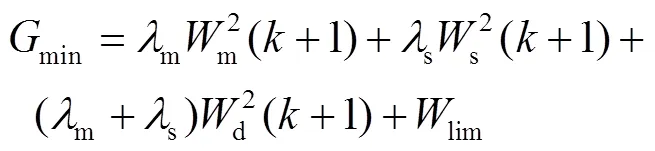
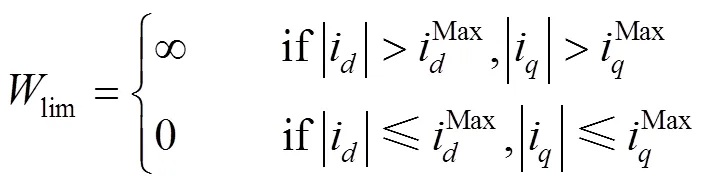
3.3 损失函数的说明

首先，本文提出的损失函数对瞬态过程和稳态过程的权重因子分别设计。m为速度误差函数，用作轴瞬态损失函数m的动态权重因子，随系统状态实时更新。给予轴稳态损失函数s一个固定的权重因子s。同时，使轴电流与轴电流达到同等的控制效果，将m和s之和设置为W的权重因子。在瞬态过程中，m远大于s，因此m和W在电压矢量选择中起决定性作用。稳态过程中，速度误差极小，m远小于s，此时电压矢量选择主要取决于s和W。由于速度误差不断收敛到零，轴损失函数可以在m和s之间非常平滑地过渡。与固定权重的损失函数相比，避免了靠经验设置权重因子的缺陷，同时可以实现MPCC瞬态下高速动态响应和稳态下的低电流纹波。

将自适应扰动观测器与含有动态权重因子的新型损失函数充分结合，得到改进后系统MPCC整体结构如图4所示。

4 仿真实验分析

为了验证所提出的控制方法的可行性和控制效果，根据系统整体结构图3，在MATLAB/Simulink搭建相应的仿真模型。文中将通过以下2种实验充分模拟永磁同步包装驱动电机在不同的工况时的动态性能和鲁棒性，并将改进后的方案与传统的MPCC的控制效果进行对比分析。

1）变载工况实验。本实验验证包装机在空载启动时的动态响应性能，以及模拟在包装生产线中发生负载突变的情景，通过对比实验来验证改进后系统的抗干扰能力和鲁棒性能。在不考虑参数失配的条件下，电机以给定转速2 000 r/min转动，0.25 s时突加负载8 N·m，在0.4 s时卸载。

2）参数失配实验。包装机在实际生产过程中会因环境温度或湿度的变化以及电机内部结构磨损老化，从而导致内部机械参数变化。本实验通过配置内部参数失配来模拟包装机在实际生产中的状态。需要指出的是，电阻参数不匹配的影响在MPCC[17]中相对较小。因此，在本组实验中主要考虑包装机内部定子电感和永磁体磁链的不确定性。

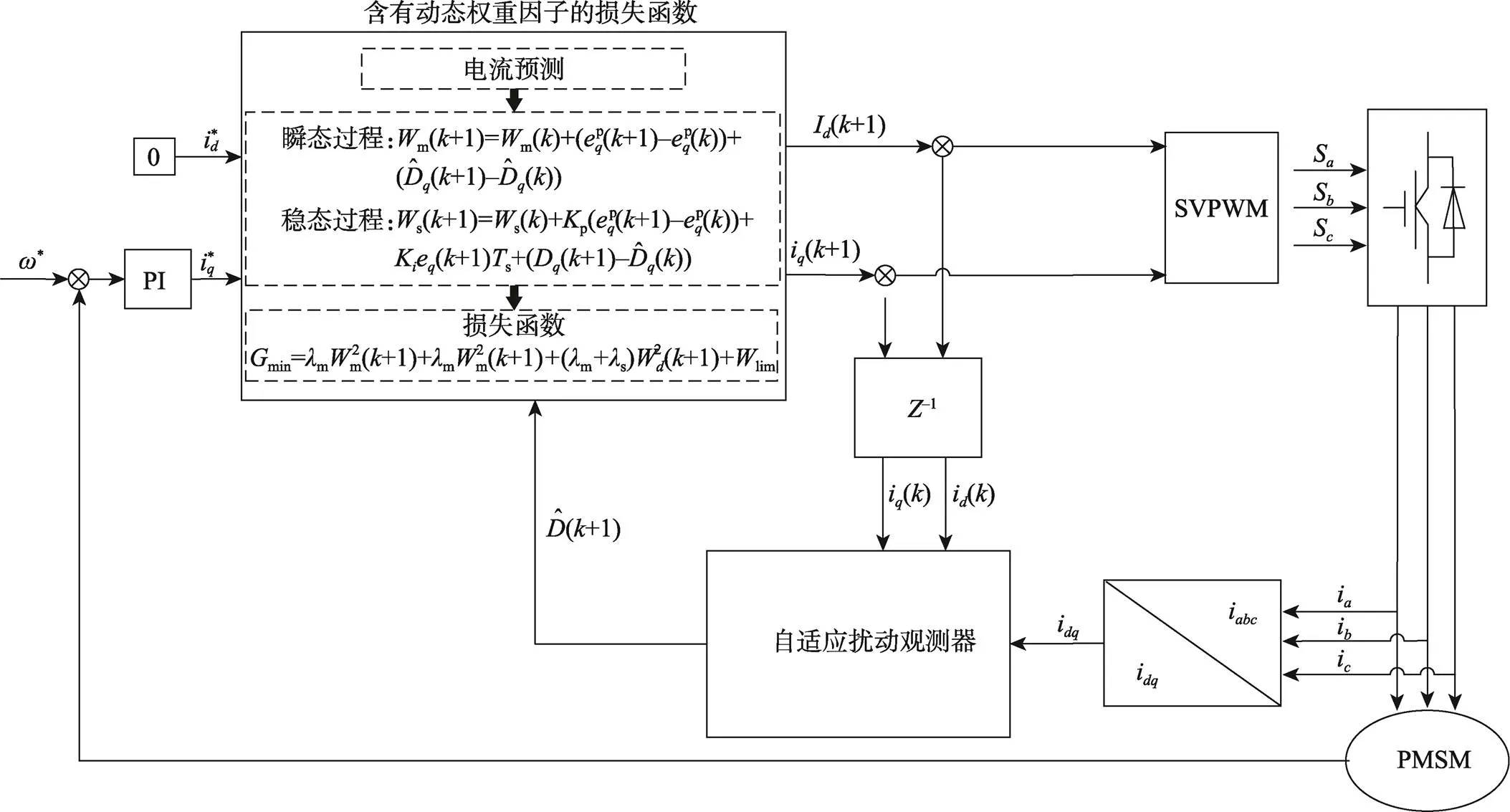
图4 基于自适应扰动观测器改进型MPCC系统结构

本文仿真实验采用的永磁同步包装机其参数如下：极对数=3，直流母线电压Uc=300 V，定子电感s=5.25 mH，定子磁链f=0.182 7 Wb。同时，对改进模型中的固定参数项进行配置，自适应扰动观测器中1=6.3、2=8.6、=0.57、=0.07；损失函数中p=2.8、i=9.3、s1。

4.1 变载工况实验

在不考虑参数失配的条件下验证本文所提出的方案应对突变负载时的鲁棒性，将电机以恒定转速2 000 r/min空载启动，0.25 s时负载突加至8 N·m，在0.4 s时负载突降至0 N·m。该实验仿真结果如图5所示，性能指标见表1。

对电机的空载启动过程进行分析，通过观察图5a中的局部放大图可发现，其快速响应的优点得到了很好的保持。这是由于在启动过程中，m对损失函数起决定性作用，所以响应时间基本接近于传统的MPCC。

通过图5b可看出，在瞬态阶段尤其是刚起步阶段，轴电流的纹波较大，其主要是由短期预测误差造成的，通过所设计的自适应扰动观测器，可以根据预测误差从而有效的补偿电流值，使电流纹波大大降低。进入稳态时，s对损失函数起决定性作用，由于预测误差大大降低，自适应扰动观测器几乎不再补偿电流进入前向通道，此时稳态的电流纹波主要由损失函数中的积分项解决。通过本文所提出方案的改进，通过图5a可知，进入稳态后的转速抖振会明显降低。通过图5c可知，轴的电流纹波得到了显著降低，因此自适应扰动观测器与动态损失函数的充分结合，对MPCC的控制性能有不错的提升。

同时，对MPCC系统面对负载突变的过程进行分析。结合表1的数据可知，在突然加载时，改进型MPCC的转速峰值降低了0.94%，调节时间缩短了70.8%。在突然减载时，改进型MPCC的转速峰值降低了0.62%，调节时间缩短了71.9%。从图5a中的局部放大图可以明显看出，无论是在突然加载还是减载的情况下，改进后MPCC受负载突变的影响远远小于传统MPCC。这得益于扰动观测器的存在，面对突然变载时，可以快速估计出电流所需的补偿值，通过计算将补偿的电流值附加到本文设计的损失函数中，筛选出更加合适的电压矢量，从而应对突然变载对系统的恶劣影响。不仅如此，在稳态性能方面，突然加载和减载时的稳态误差分别减小了81.2%和82.1%，这得益于在稳态时的损失函数中引入积分环节，使系统可以更加平稳的运行。

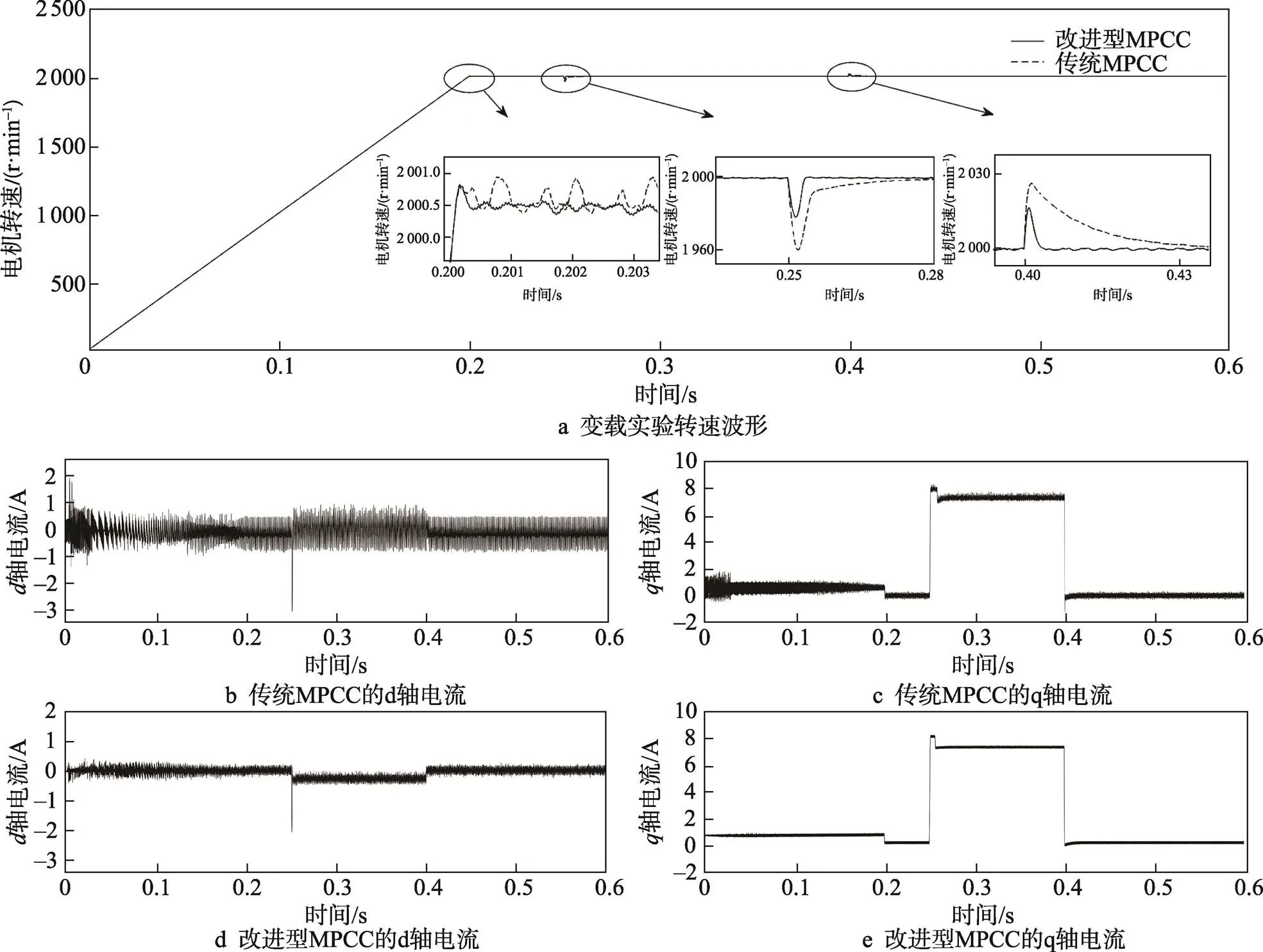
图5 变载工况实验

表1 变载实验仿真性能指标对比

Tab.1 Comparison of variable load experimental performance indicators

4.2 参数失配实验

在本小节的实验中，将电机的给定转速均设置为2 000 r/min，让电机以空载状态启动，在0.25 s时给予系统负载转矩为8 N·m。通过与传统MPCC的对比实验，以验证改进后MPCC系统的参数鲁棒性。

4.2.1 定子电感失配

为了验证改进后方案的参数鲁棒性，将定子电感值设置为标称值的50%、75%、200%，其运行结果如图6所示。通过观察图6a可知，传统的MPCC在应对75%电感失配时，其-轴电流纹波会明显增大，这得益于自适应扰动观测器的作用。由图6b得知，改进后MPCC的电流纹波会明显下降。通过观察图6c可知，在应对50%电感失配时，尤其在0.25 s增加负载后，传统MPCC的电流会产生严重的毛刺现象，此时已经丧失对系统的控制能力。由图6d可知，改进后的MPCC面对50%电感失配时，依然展现了较强的鲁棒性。同样，当电感失配值大于标称值，为标称值的200%时，通过观察图6e和图6f可知，改进后的MPCC与传统方案的MPCC相比，电流纹波也会得到明显改善。

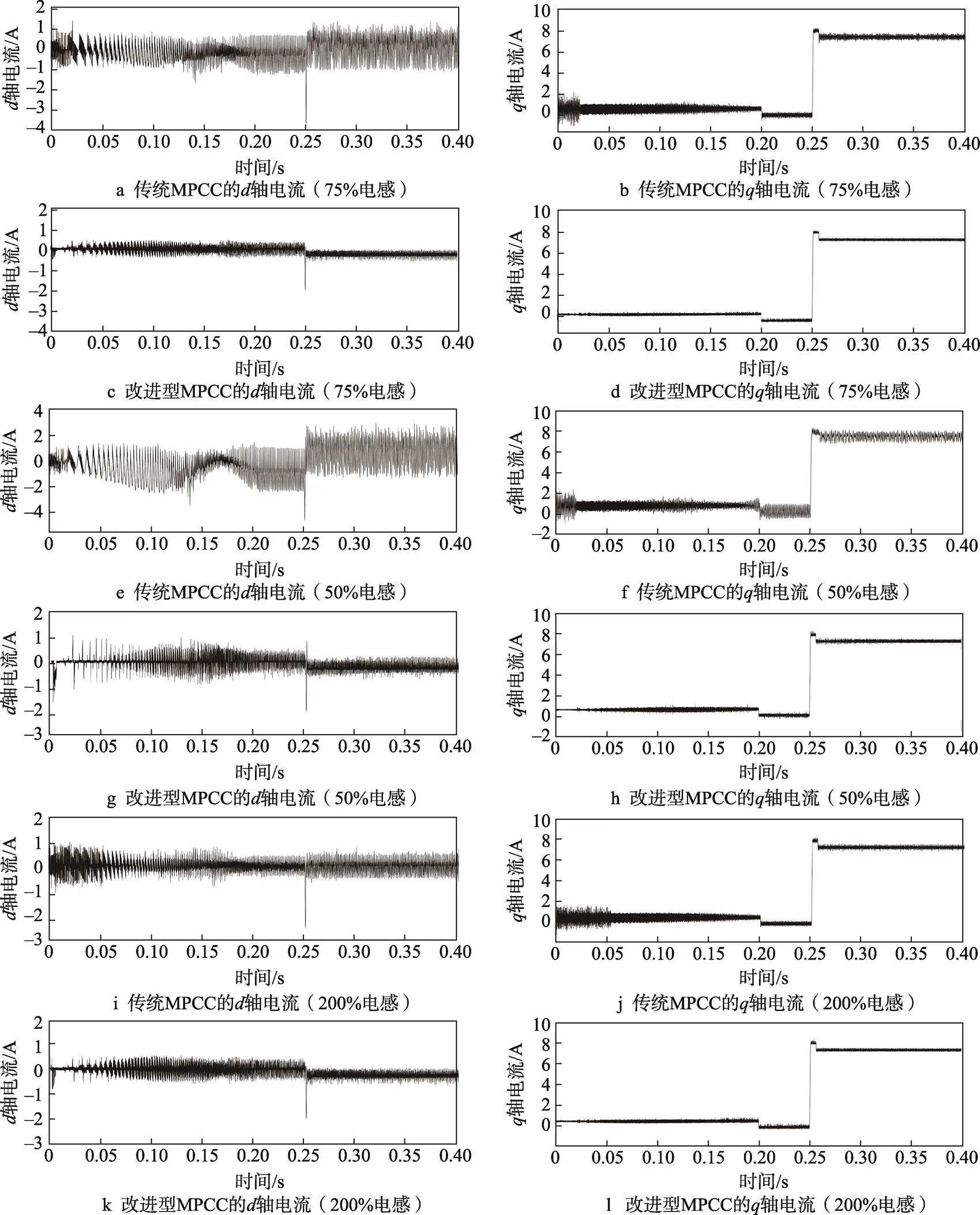
图6 电感失配实验

4.2.2 永磁体磁链失配

除定子电感之外，永磁体磁链也会随电机运动状态改变而产生变化，将磁链值设置为标称值的65%、200%时，其运行结果如图7所示。经过多次实验，当永磁体磁链值为标称值的65%及以下时，观察图7a可知，传统MPCC的轴电流在增加负载后，无法收敛到参考电流，则系统的输出扭矩将不能满足负载需求，达到最大永磁体磁链失配的最小值。当磁链值为标称值的200%时，观察图7c可知，传统MPCC的轴电流在增加负载的瞬间，会产生一个剧烈的向上冲击电流，从而超出系统的峰值扭矩。由图7d可知，改进后MPCC的控制效果受永磁体磁链失配的影响会明显降低。

4.2.3 3种主要参数失配

为了充分验证所提出方案的优越性，使其更能适应极端恶劣的实际工况环境，考虑定子电感、定子电阻、永磁体磁链同时失配的条件下进行实验。设置s=5s、s=0.5s和f=1.8f，其仿真结果如图8所示。观察图8a可知，当传统的MPCC应对多参数同时失配时，-轴电流会在增加负载后产生剧烈的电流振荡。然而观察图8b可知，改进后的MPCC系统在面临此情况时，-轴电流的性能仍可以保持准确且较低的电流纹波。

通过以上3种参数失配情况的仿真结果表明，与传统的MPCC相比，改进后的MPCC系统显示出更加平稳的电流响应。充分验证了改进后系统具备极强的参数鲁棒性，使电机可以在各种工况下更加平稳高效的运行。

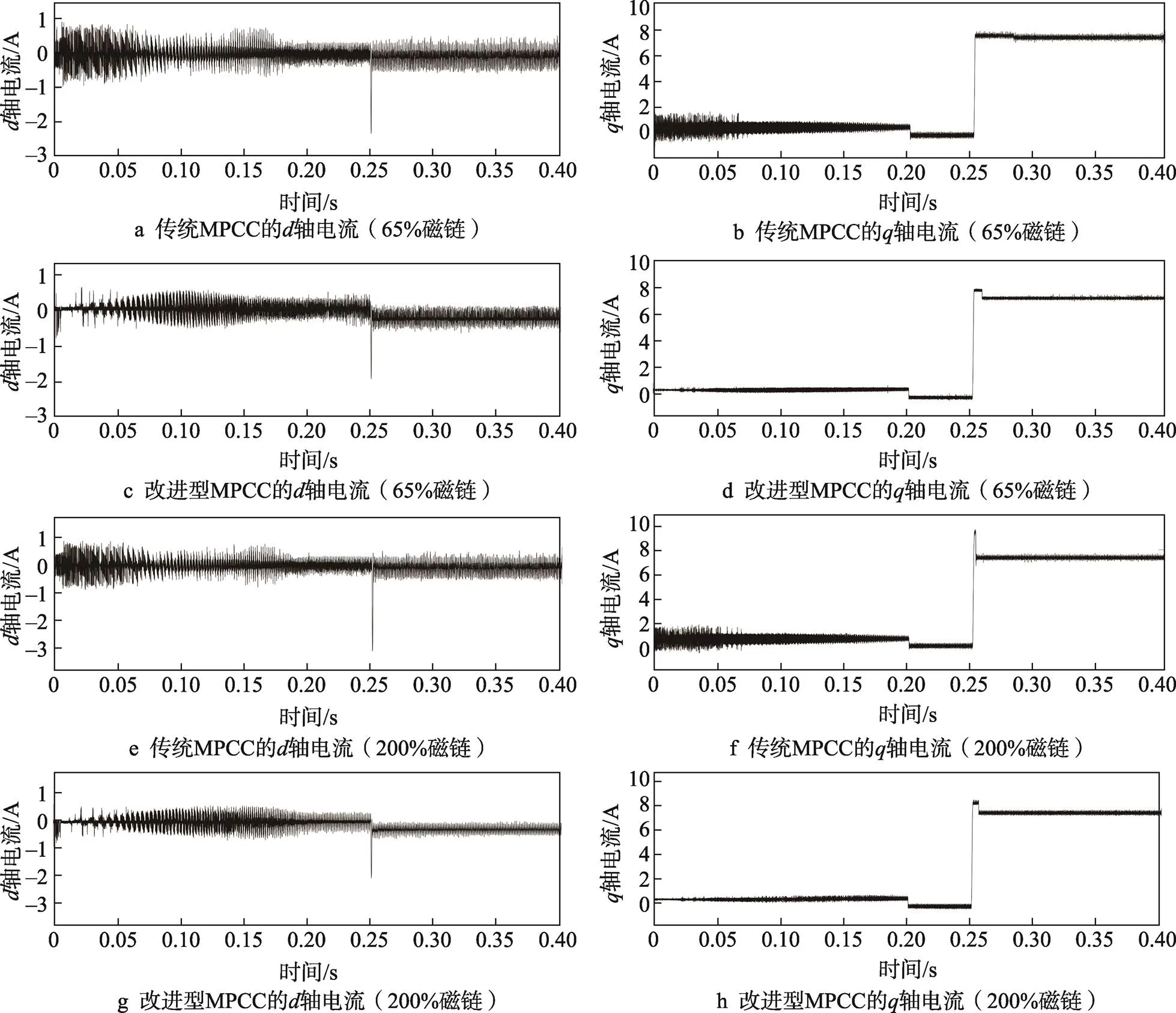
图7 永磁体磁链失配实验

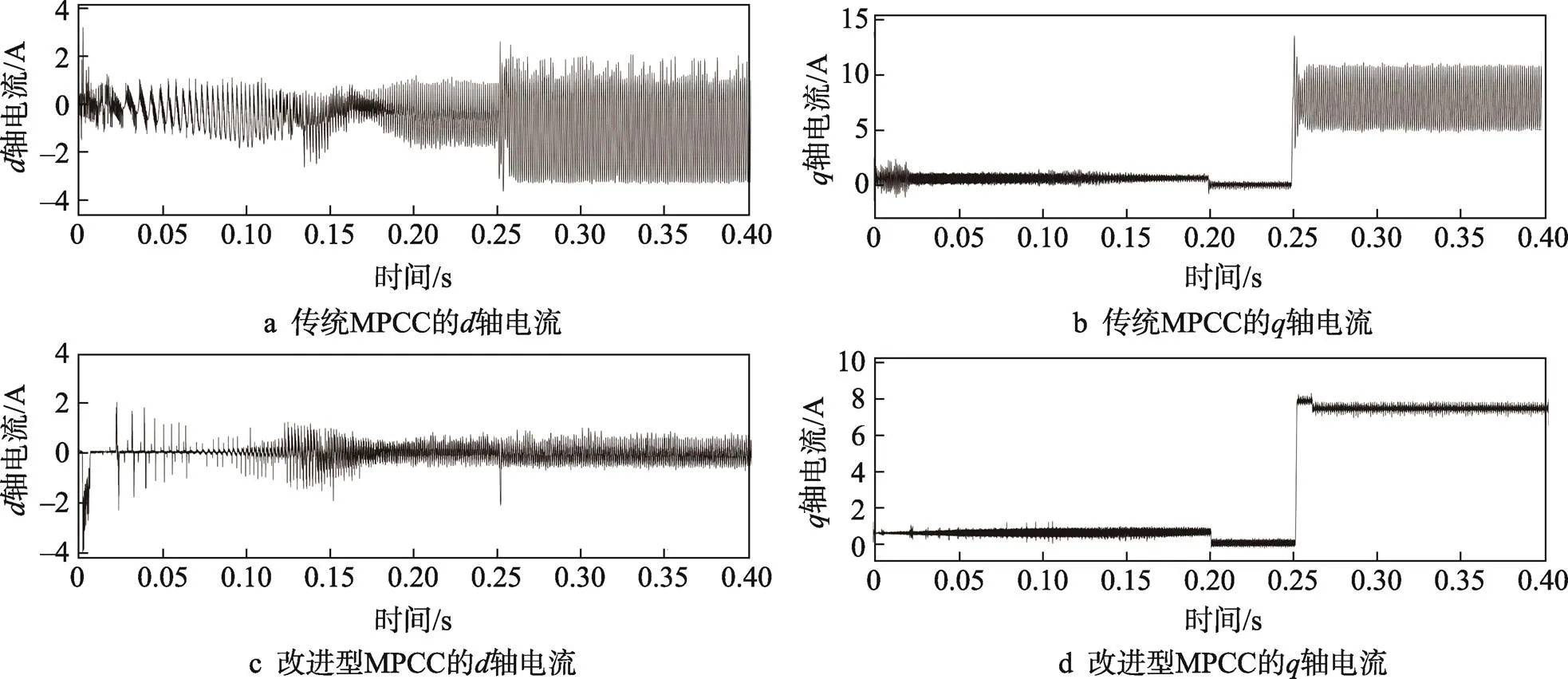
图8 3种参数失配实验

5 结语

本文主要针对永磁同步包装机MPCC控制系统，在应对内部参数失配以及负载突变时鲁棒性差的问题，提出了一种基于扰动观测器的改进型MPCC控制方案。首先，通过设计自适应可变增益扰动观测器，利用当前预测误差在线估计出电流所需的补偿值，并将系统的瞬态和稳态过程分别进行考虑，通过动态权重因子将2种系统状态有机的结合，再引入扰动观测器估计的电流补偿值，构成了一种新型损失函数。通过仿真果表明，本文所提出的改进型MPCC系统既能够在有效应对包装机因环境或者内部结构老化造成的内部参数失配现象及外部变载问题的同时，还能够保持MPCC高速动态特性的优点。文中方法对MPCC控制策略在永磁同步包装机上的应用有着借鉴意义。

[1] 秦艳忠, 阎彦, 陈炜, 等. 永磁同步电机参数误差补偿-三矢量模型预测电流控制[J]. 电工技术学报, 2020, 35(2): 255-265.

QIN Yan-zhong, YAN Yan, CHEN Wei, et al. Three-Vector Model Predictive Current Control Strategy for Permanent Magnet Synchronous Motor Drives with Parameter Error Compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 255-265.

[2] LI Teng, SUN Xiao-dong. Improved Model Predictive Robust Current Control for Permanent Magnet Synchronous Hub Motor[C]// 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), IEEE, 2021: 147-151.

[3] 冯凌, 付建国, 廖丽诚, 等. 一种改进的永磁同步牵引电机低开关频率模型预测直接转矩控制策略[J]. 中国电机工程学报, 2021, 41(21): 7507-7516.

FENG Ling, FU Jian-guo, LIAO Li-cheng, et al. An Improved Model Predictive Direct Torque Control Strategy for Permanent Magnet Synchronous Traction Motor with Low Switching Frequency[J]. Proceedings of the CSEE, 2021, 41(21): 7507-7516.

[4] YOUNG H A, PEREZ M A, RODRIGUEZ J. Analysis of Finite-Control-Set Model Predictive Current Control with Model Parameter Mismatch in a Three-Phase Inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3100-3107

[5] YUAN Xin, ZHANG Shuo, ZHANG Cheng-ning.. Improved Model Predictive Current Control for SPMSM Drives with Parameter Mismatch[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 852-862.

[6] 王艳, 刘旭东. 基于扰动补偿的永磁同步电机预测位置控制[J]. 控制工程, 2022, 29(5): 828-836.

WANG Yan, LIU Xu-dong. Predictive Position Control of Permanent Magnet Synchronous Motor Based on Disturbance Compensation[J]. Control Engineering of China, 2022, 29(5): 828-836.

[7] XIA Chang-liang, WANG Meng, SONG Zhan-feng, et al. Robust Model Predictive Current Control of Three-Phase Voltage Source PWM Rectifier with Online Disturbance Observation[J]. IEEE Transactions on Industrial Informatics, 2012, 8(3): 459-471.

[8] 赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2385.

ZHAO Kai-hui, DAI Wang-ke, ZHOU Rui-rui, et al. Novel Model-Free Sliding Mode Control of Permanent Magnet Synchronous Motor Based on Extended Sliding Mode Disturbance Observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2385.

[9] YANG Ming, LANG Xiao-yu, LONG Jiang, et al. Flux Immunity Robust Predictive Current Control with Incremental Model and Extended State Observer for PMSM Drive[J]. IEEE Transactions on Power Electronics, 2017, 32(12): 9267-9279.

[10] MOHAMED Y A I. Design and Implementation of a Robust Current-Control Scheme for a PMSM Vector Drive with a Simple Adaptive Disturbance Observer[J]. IEEE Transactions on Industrial Electronics, 2007, 54(4): 1981-1988.

[11] MOHAMED Y A R I, EL-SAADANY E F. A Current Control Scheme with an Adaptive Internal Model for Torque Ripple Minimization and Robust Current Regulation in PMSM Drive Systems[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 92-100.

[12] 王立俊, 赵吉文, 董菲, 等. 基于自适应内模观测器的永磁同步直线电机高带宽强鲁棒预测电流控制策略研究[J]. 中国电机工程学报, 2019, 39(10): 3098-3106.

WANG Li-jun, ZHAO Ji-wen, DONG Fei, et al. Research on High Bandwidth and Strong Robust Predictive Current Control Strategy of Permanent Magnet Synchronous Linear Motor Based on Adaptive Internal Model Observer[J]. Proceedings of the CSEE, 2019, 39(10): 3098-3106.

[13] 李耀华, 秦辉, 苏锦仕, 等. 基于模糊控制的动态权重系数表贴式永磁同步电机模型预测转矩控制系统[J]. 电机与控制应用, 2020, 47(3): 1-7.

LI Yao-hua, QIN Hui, SU Jin-shi, et al. Model Predictive Torque Control of SPMSM with Dynamic Weight Coefficient Based on Fuzzy Control[J]. Electric Machines & Control Application, 2020, 47(3): 1-7.

[14] 梅容魁, 于新红. 基于PSO的模型预测速度控制权重系数自整定[J]. 微特电机, 2022, 50(5): 42-46.

MEI Rong-kui, YU Xin-hong. Self-Tuning of Weight Coefficients for Model Predictive Speed Control Based on PSO[J]. Small & Special Electrical Machines, 2022, 50(5): 42-46.

[15] MACHADO O, SANCHEZ P, RODRÍGUEZ F, et al. A Neural Network-Based Dynamic Cost Function for the Implementation of a Predictive Current Controller[J]. IEEE Transactions on Industrial Informatics, 2017(99): 1.

[16] LIU Xi-cai, ZHOU Li-bing, WANG Jin, et al. Robust Predictive Current Control of Permanent-Magnet Synchronous Motors With Newly Designed Cost Function[J]. IEEE Transactions on Power Electronics, 2020(99): 1.

[17] SIAMI M, KHABURI D A, ABBASZADEH A, et al. Robustness Improvement of Predictive Current Control Using Prediction Error Correction for Permanent- Magnet Synchronous Machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3458-3466.

Predictive Current Control of PMSM Model Based on Adaptive Disturbance Observer

JIN Ai-juan, ZHANG Jin-song, LI Shao-long

(University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to design a predictive current control strategy of model based on adaptive disturbance observer, in order to realize the high-performance control of the packaging automation production line and solve the problem that the permanent magnet synchronous packaging drive motor is more sensitive to disturbance in the predictive current control of model. Firstly, an adaptive disturbance observer was designed by the prediction error. For the internal and external uncertain disturbances suffered by the system, the disturbance observer estimated the total disturbance and made compensation in the form of current. Moreover, the transient process and steady-state process of the system were considered separately, and a new loss function with dynamic weight factors was designed. The MATLAB/SIMULINK simulation showed that, compared with the traditional control method, the method proposed could maintain high-speed dynamic response in transient state and low current ripple in steady state, and show excellent performance in coping with parameter mismatch and load mutation. It has better steady-state performance and anti-interference ability. The method proposed can effectively improve the dynamic performance and robustness of the system, making the improved system more suitable for the application scenarios of packaging machines.

permanent magnet synchronous motor; adaptive method; disturbance observer; dynamic weighting factor

TB486；TM341

A

1001-3563(2023)23-0171-10

10.19554/j.cnki.1001-3563.2023.23.021

2023-02-13

国家自然科学基金(11502145)

责任编辑：曾钰婵