果蔬微孔包装膜开孔模型的建立与验证

余立，林渊智*，王永祥

果蔬微孔包装膜开孔模型的建立与验证

余立1,2，林渊智1,2*，王永祥3

（1.福建技术师范学院，福建 福清 350300；2.食品软塑包装技术福建省高校工程研究中心，福建 福清 350300；3.福融新材料股份有限公司，福建 福清 350399）

建立一种能够有效控制果蔬气调包装袋内气体浓度的微孔膜开孔模型，以便有效延长果蔬保质期。通过分析气体在薄膜微孔中的透气机理，并结合原膜透气机理和果蔬自身呼吸速率，建立薄膜开孔模型。以樱桃为包装对象，通过对比包装容器内实测气体浓度与预测气体浓度，判别开孔模型的准确性。开孔模型3-1设计的包装方案，其内部实测氧气浓度与预测氧气浓度最吻合；模型1-1与模型1-2计算的开孔方案其孔径达到毫米级，开孔数量达到100，不适合用于薄膜开孔。模型3-2、模型2-1和模型2-2设计的包装方案，其内部实测气体浓度与预测气体浓度不一致。微孔直径大小会直接影响气体分子在微孔中的扩散形式和开孔模型的准确性。当微孔直径在100 µm时，利用Fick定律和Kundsen定律的扩散系数k构建的数学模型能够准确地控制包装袋内的O2浓度与CO2浓度，依据该模型制作的微孔气调包装袋能够有效延长樱桃的保质期。

开孔模型；微孔膜；薄膜透气机理

果蔬气调包装，主要通过在包装容器（袋）内营造低O2高CO2的气调氛围抑制果蔬呼吸速率，从而延长其货架期[1]。普通薄膜由于气体渗透率不能改变，无法匹配果蔬呼吸速率，易导致果蔬因缺氧（无氧呼吸）而腐败[2]。而激光微孔技术可以在原膜上开出不同数量、不同直径的小孔，调节单位时间内薄膜透气量[3]。

开孔后的塑料薄膜，气体会同时通过原膜和微孔进行气体交换。目前，原膜的气体交换模型公认适用Fick定律[4]，而微孔处的气体交换模型大多是经验模型。如李方等[5]建立的微孔透气量与微孔数量、微孔直径、薄膜面积、薄膜厚度等参数之间的经验模型；Mahajan等[6]利用Arrhenius方程引入温度参数的经验模型；Mastromatteo等[7]利用在同一薄膜上的16种不同微孔参数建立的经验模型。这些经验模型在某一种特定的薄膜上具有较准确的预测性。但是，当更换薄膜品种后，就需要重新采样数据（连续不断地改变微孔数量、微孔直径、薄膜面积、薄膜厚度等参数，并检测相应的气体透过量），工作量巨大，操作繁琐。本课题则是利用Fick定律，通过分析气体分子在通过微孔时所受的阻力，修改气体扩散系数的方法，确立薄膜微孔处的理论气体交换模型（该模型计算得出的微孔处的透气量不依赖薄膜种类，与薄膜透气系数无关），从而推导出果蔬微孔膜的开孔模型，并在一种果蔬（樱桃）上进行了试验验证。该理论模型仅需要少量数据即可完成计算，可快速应用于果蔬微孔气调包装开孔。

1 微孔膜透气机理研究

微孔气调包装膜主要是通过原膜的渗透性和微孔，实现包装容器内外的气体交换。由于每种果蔬的呼吸速率不同，仅靠原膜的渗透作用很难精确控制包装容器内气体浓度，因此需要在薄膜表面开出一定数量的微孔来调节包装容器内气体浓度。

O2和CO2会同时通过原膜和微孔扩散。薄膜未开孔部分，气体分子的交换基于Fick定律；而微孔部分，气体是如何通过微孔的，目前还没有成熟的理论模型。

1.1 原膜的气体交换机理

对于薄膜未开孔部分，气体首先会溶解在薄膜内，当达到饱和后，气体将由高浓度向低浓度进行扩散。在单位时间内，单位面积下气体透过薄膜的总量为J[8]，见式（1）。

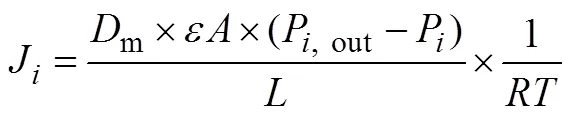
式中：J为气体单位时间内透过薄膜的量，mol/h；m为气体扩散系数，m2/h；为薄膜面积，m2；为薄膜厚度，m；P，out、P别为气体在大气中的分压和在容器内的分压，Pa；为理想气体常数，8.314；为热力学温度，K。

1.2 微孔的气体交换机理

气体通过微孔扩散，一定时间内总的扩散量主要取决于气体分子受到的阻力。其阻力主要来源于气体分子之间的碰撞摩擦或气体分子与孔壁的碰撞摩擦。根据微孔中气体分子所受阻力的不同，建立了3种微孔气体交换模型。

1）假设气体分子在微孔中流动的阻力主要源于气体分子间的碰撞摩擦，而气体分子与孔壁的摩擦阻力忽略不计，此时气体分子在微孔中流动的情况近似等同于在空气中的扩散，扩散速率只与气体的浓度梯度有关。因此微孔中的气体分子扩散仍适用Fick定律，但此时扩散系数改为气体分子在空气中的扩散系数。

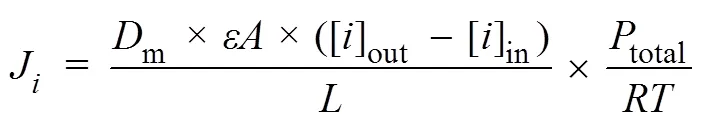
式中：J为气体单位时间透过薄膜的量，mol/h；为薄膜面积，m2；为薄膜厚度，m；为开孔率，%；m为气体在空气中的扩散系数，m2/s，常温常压（25 ℃，0.1 MPa）下O2在空气中的扩散系数m=0.201×10−4m2/s，CO2在空气中的扩散系数m=0.156×10−4m2/s[9]；[]out、[]in分别为气体在大气中的浓度和气体在容器内的体积分数，%；total为大气压强，Pa；

2）假设气体分子在微孔中流动所遇阻力部分来源于分子间的碰撞摩擦，部分来源于气体分子同孔壁的摩擦，此时气体分子的运动规律类似于黏性流动[10]，气体分子在微孔中的扩散符合Hagen-Pouiseville定律：

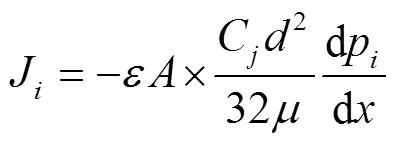
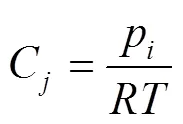
由式（3）求定积分得：

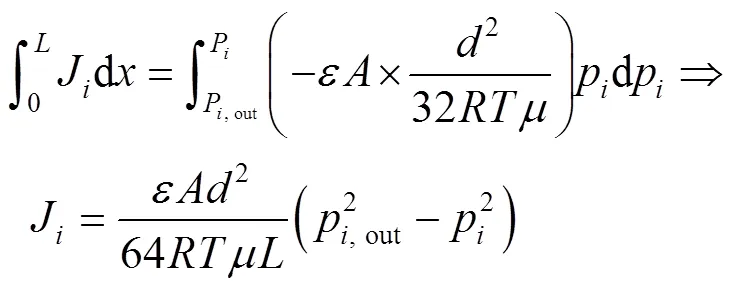
3）气体分子在微孔中流动时同孔壁的碰撞概率要大于气体分子间的碰撞概率，此时气体分子在微孔中的扩散规律近似于气体分子在原膜中的扩散，因此其仍然适用于Fick定律，但其扩散系数k为Kundsen系数[12]。

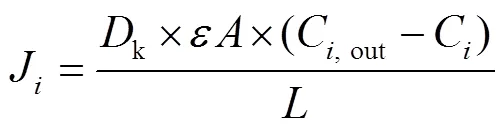
Kundsen系数为：

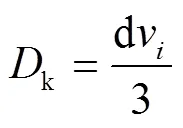
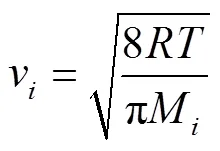
根据道尔顿定律[10]：

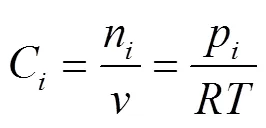
将式（5）和式（6）代入式（4）得：

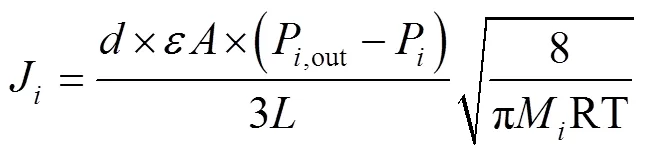
1.3 包装容器气体交换理论模型构建

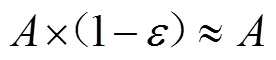
基于Fick定律的微孔膜气体交换模型

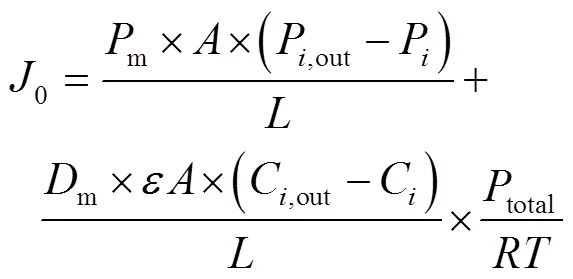
基于Hagen-Pouiseville定律的微孔膜气体交换模型：

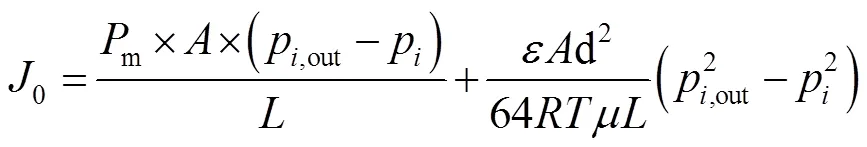
基于Kundsen系数的微孔膜气体交换模型：

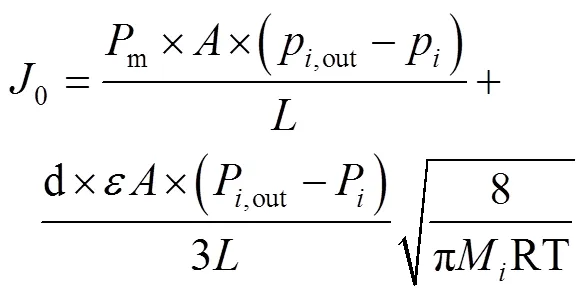
2 设计与实验

2.1 原料与仪器

主要原料：农场新鲜采摘樱桃（品种为黑甜，产地为福建）；自制玻璃密封箱，容积为3.3 L；自制PP流延膜，厚度为30 µm，O2渗透系数为1.1364×10−12mol∙m/(m2∙h∙Pa)；CO2渗透系数为3.358 8×10−13mol∙m/(m2∙h∙Pa)。

主要仪器：顶空气体分析仪（HGA-02），济南兰光机电技术有限公司；薄膜测厚仪（CHY-CB），济南兰光机电技术有限公司；薄膜渗透系数检测仪（G2/131），济南兰光机电技术有限公司；激光打孔机（HY-C100W），广州华越激光设备有限公司；PER30-S激光打孔机，荷兰Perftec公司。

2.2 果蔬呼吸速率测定

采用密闭系统法[13]，每组将0.15 kg樱桃装入自制密封箱（不透气），置于常温常压（25 ℃、0.1 MPa）下储藏，每隔1 h用顶空气体分析仪检测密封箱内O2的体积分数与CO2的体积分数，共3组。呼吸速率用式（11）进行计算，结果取平均值。

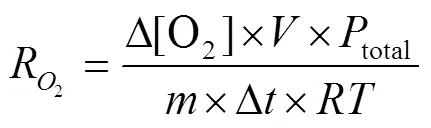
2.3 微孔膜开孔方案设计

利用果蔬的呼吸作用，使包装容器内的气体浓度达到动态平衡[14]，包装袋内的O2的体积分数和CO2的体积分数维持在预设的气体浓度值附近。

采用三边封形式制作包装袋，包装袋长为30 cm、宽为20 cm、总面积为0.12 m2，薄膜厚度为30 µm，被包装樱桃质量为0.15 kg，樱桃理想储藏气体体积分数预设：[O2]为5%，[CO2]为10%。根据以上参数计算出相应的开孔方案。

樱桃的呼吸速率模型[15]如下：

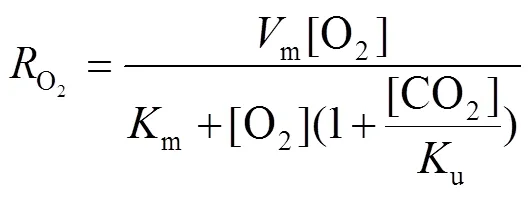
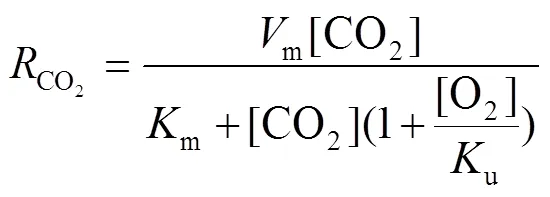
式中：O2为基于O2的果蔬呼吸速率，mol/(kg∙h)；O2为基于CO2的果蔬呼吸速率，mol/(kg∙h)；m为果蔬最大呼吸速率，mol/(kg∙h)；[O2]为平衡时氧气的体积分数，%；[CO2]为平衡时二氧化碳的体积分数，%；m为米氏常数；u为抑制米氏常数。

当包装容器内外达到动态平衡时，果蔬呼吸消耗的O2等于通过微孔膜渗透进来的O2[16]（产生的CO2等于排出的CO2），分别用式（13）、式（14）和式（15）表示。求解式（13）、式（14）和式（15），即得到6种开孔模型。

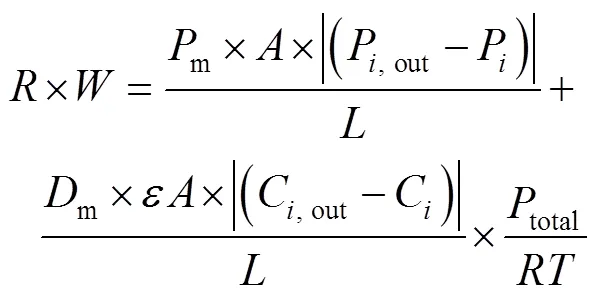
将式（12）代入式（13），得开孔模型1-1见式（14）和开孔模型1-2见式（15）。

开孔模型1-1：

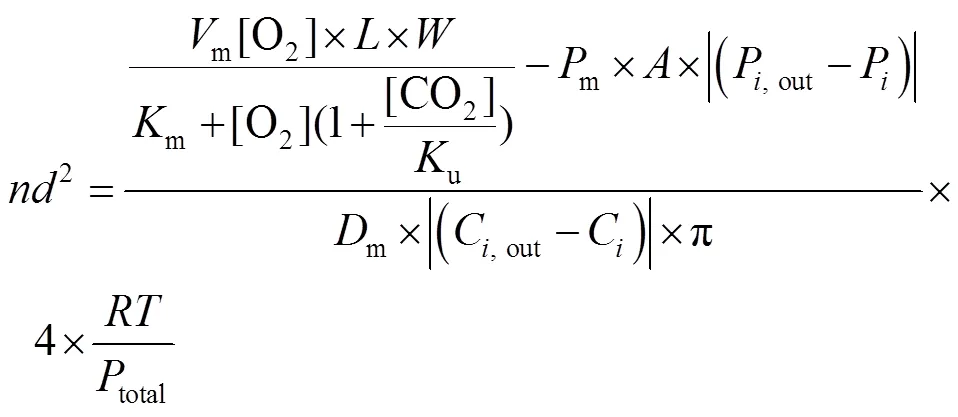
开孔模型1-2：

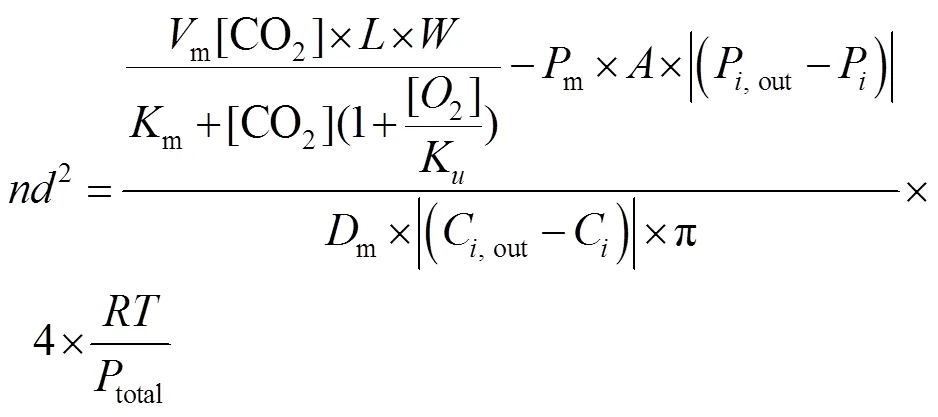
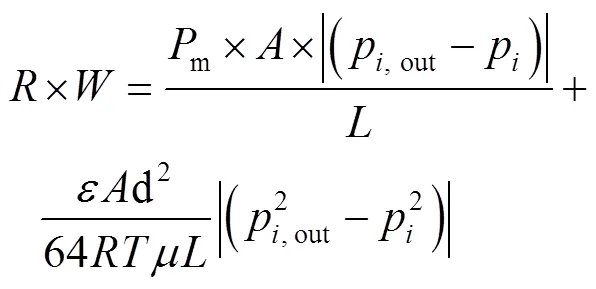
将式（12）代入式（16），得开孔模型2-1见式（17）和开孔模型2-2见式（18）。

开孔模型2-1：

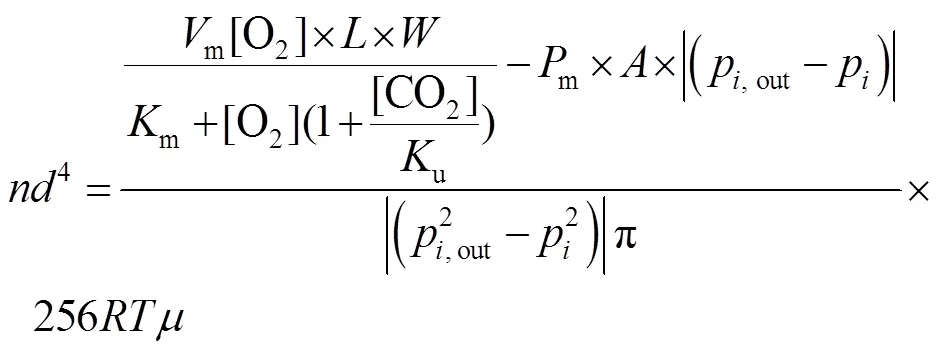
开孔模型2-2：

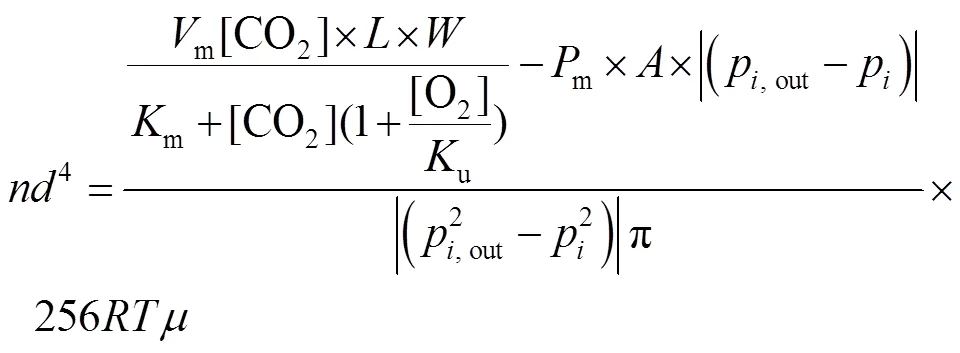
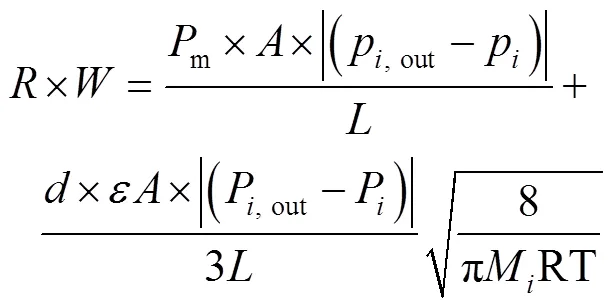
将式（12）代入式（19），得到开孔模型3-1见式（20）和开孔模型3-2见式（21）。

开孔模型3-1：

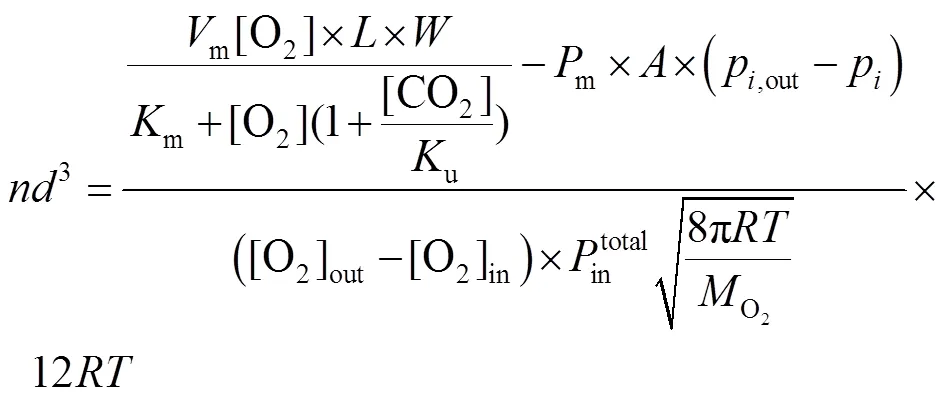
开孔模型3-2：

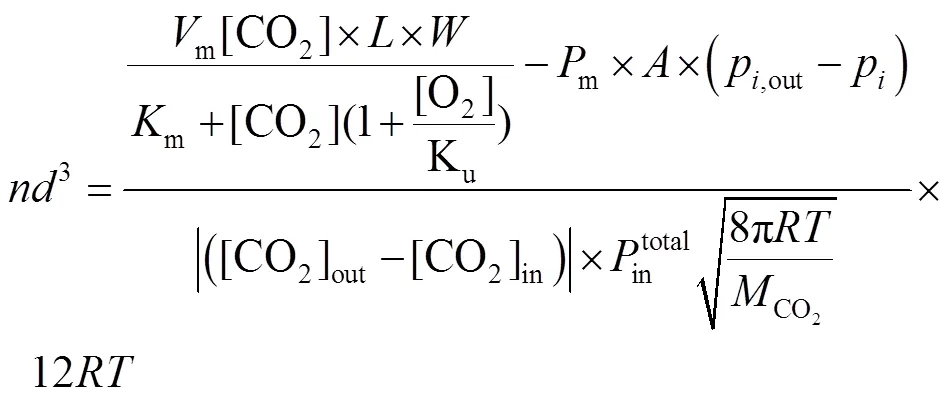
2.4 果蔬微孔包装袋气体浓度检测

设计3组平行实验，每组根据模型开孔方案使用激光打孔机在薄膜上打孔，将包装袋置于25 ℃、0.1 MPa的环境中储藏，每隔24 h用顶空气体分析仪检测袋内气体浓度。3组平行实验实测气体浓度如相差不超过1%，则取平均值作为实验结果，否则重新检测。

3 结果与分析

3.1 樱桃呼吸速率模型

将常温常压下每间隔1 h内测得的O2浓度变化量与CO2浓度变化量，代入式（11）计算出相应的呼吸速率[17-18]，通过线性回归分析拟合出樱桃的呼吸速率模型，见式（22）和式（23）。

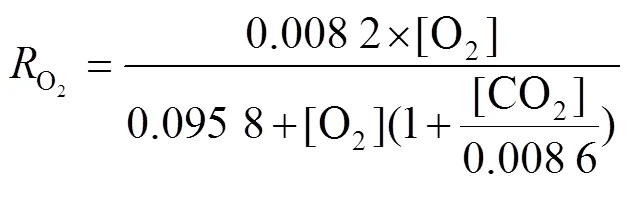
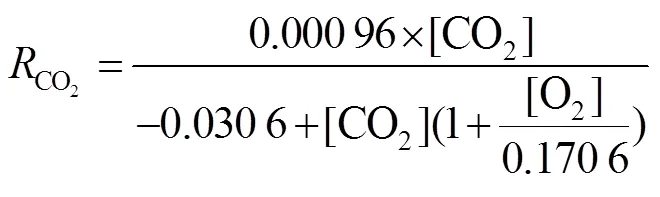
3.2 开孔方案计算

将樱桃呼吸速率方程相关参数、预设气体浓度和包装面积等数据代入式（13），计算得到开孔模型1-1和开孔模型1-2，分别见式（24）和式（25）。

模型1-1：

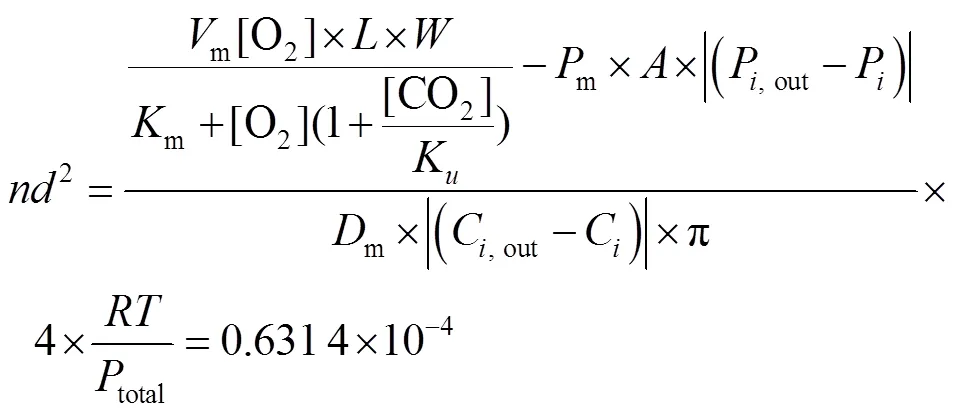
模型1-2：

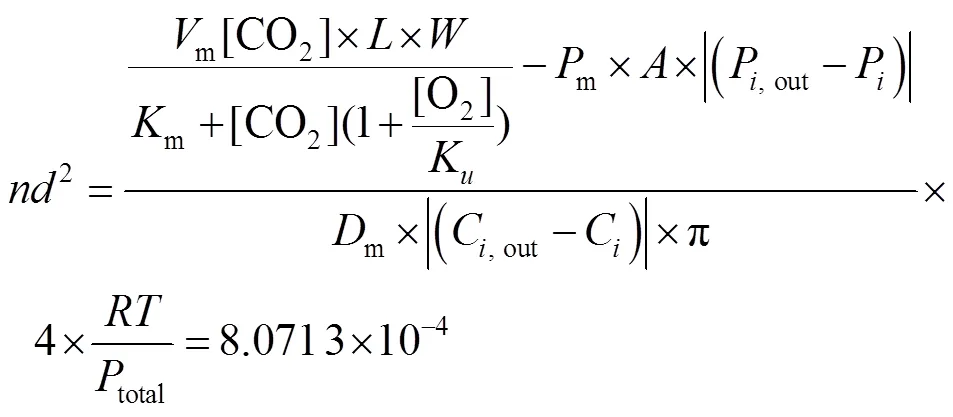
根据结算结果，得出第1种模型开孔方案如表1所示。

表1 模型1开孔方案

Tab.1 Perforation scheme for model 1

将果蔬相关参数代入模型式（14），得到开孔模型2-1和开孔模型2-2，分别见式（26）和式（27）。

模型2-1：

模型2-2：

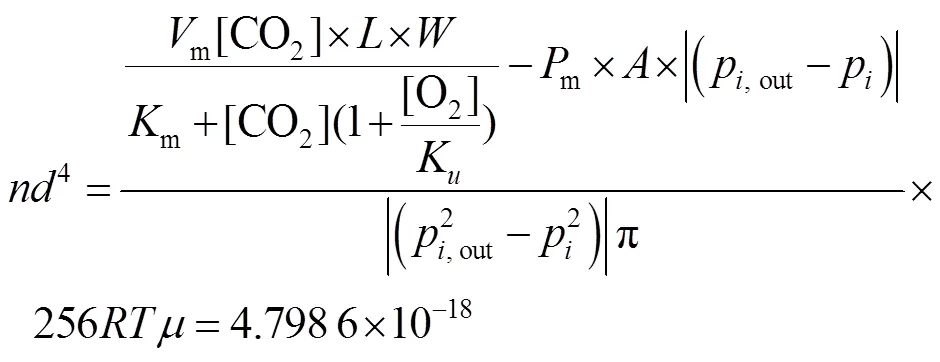
根据结算结果，得出第2种模型开孔方案如表2所示。

表2 模型2开孔方案

Tab.2 Perforation scheme for model 2

将果蔬相关参数代入模型式（15），得到开孔模型3-1和开孔模型3-2，分别见式（28）和式（29）。

模型3-1：

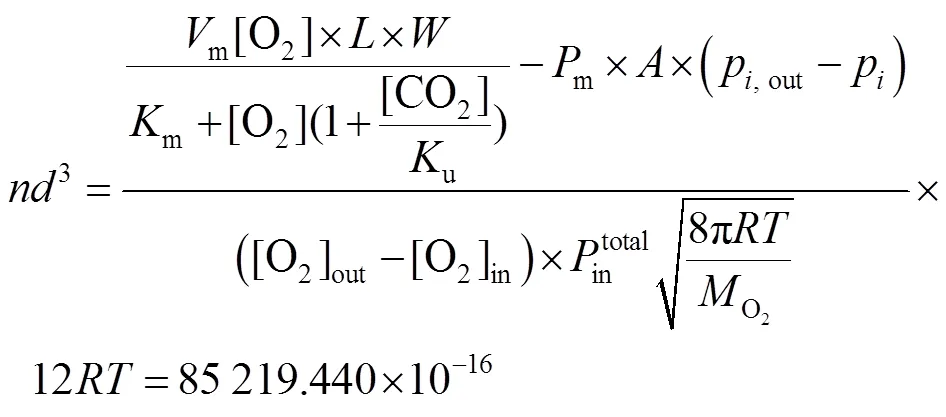
模型3-2：

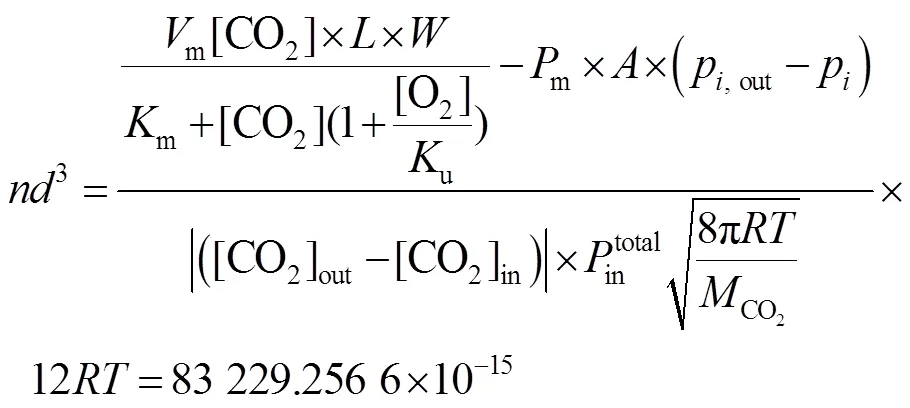
根据结算结果，得出第3种模型开孔方案，如表3所示。

表3 模型3开孔方案

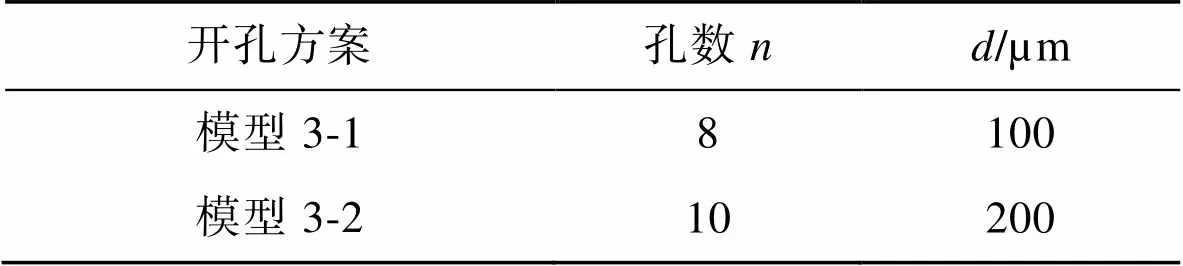
Tab.3 Perforation scheme for model 3

据以上开孔模型计算结果，模型1-1和模型1-2计算得到的开孔数量较多且孔径过大（达到毫米级）。说明气体分子在微孔中流动时，只有在孔径足够大的情况下，才能判定其阻力主要源于气体分子间的碰撞摩擦，而忽略气体分子与孔壁的摩擦。但是孔径过大且孔的数量太多，会严重影响果蔬包装袋的外观和机械强度，因此认为模型1-1和模型1-2不适合用于果蔬微孔包装膜开孔。模型2-1、模型2-2、模型3-1、模型3-2的开孔方案与无包装和密闭不开孔包装方案在常温常压条件下进行对照实验，具体方案如表4所示。

表4 开孔方案

Tab.4 Perforation scheme

3.3 各包装容器内实测气体浓度及开孔模型验证

各包装方案的气体体积分数的变化变化见图1和图2。

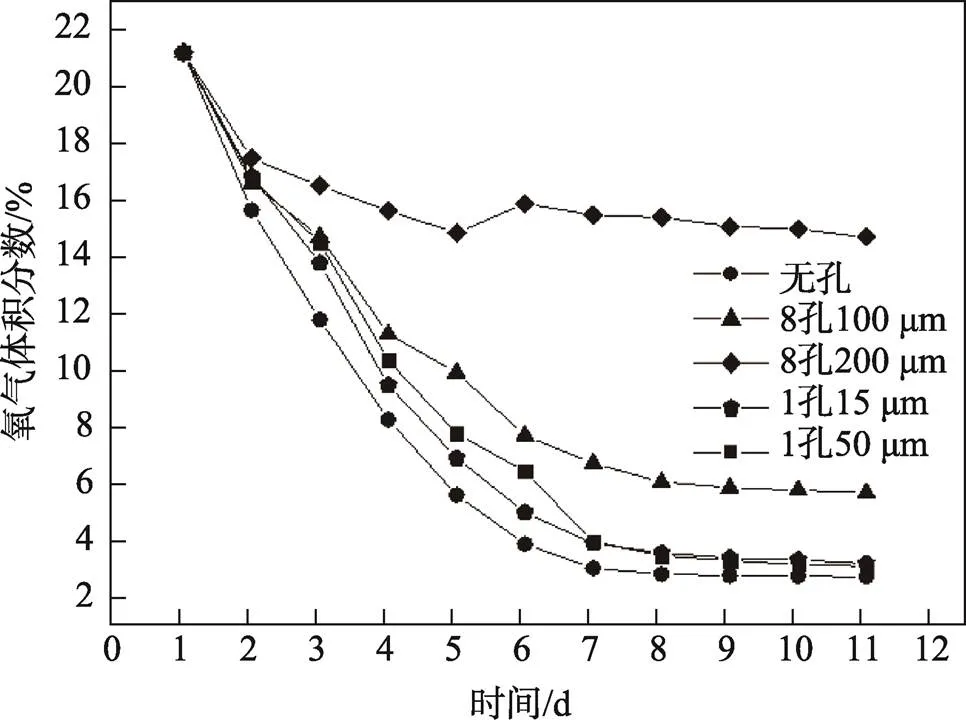
图1 包装容器内O2体积分数变化

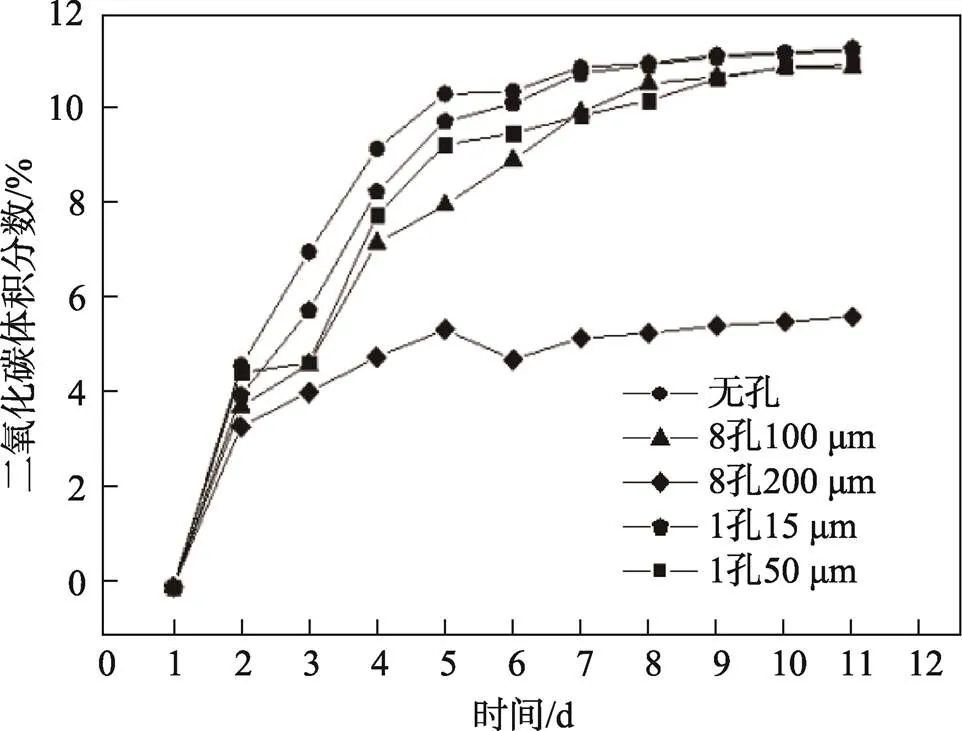
图2 包装容器内CO2体积分数变化

各组包装方案中出现第1粒樱桃腐烂的时间见表5。

结果显示，模型3-1计算得出的方案（8孔100 µm）使包装袋内的气体浓度在第7天开始进入动态平衡，且O2的体积分数与CO2的体积分数分别维持在5%和10%左右，与预测气体浓度（[O2]为5%，[CO2]为10%）接近（实验进行至第11天该方案出现1粒坏果，且该方案最晚出现坏果，则将第11天定为实验结束时间）。模型3-2计算得出的方案（10孔200 µm）的包装袋内的气体浓度则在第4天开始进入动态平衡，且O2的体积分数与CO2的体积分数分别维持在15%和5%左右，该方案实测气体浓度与预测气体浓度不符。这可能是由于200 µm的孔径对O2分子和CO2分子来说太大，气体分子在微孔中流动时与孔壁的碰撞概率小于气体分子之间的碰撞概率，故不能将气体分子在微孔中的扩散近似看成在原膜中的扩散，即不能采用Kundsen系数替代Fick定律中薄膜气体渗透散系数k的方法建模。因此判定模型3-2不适用于果蔬微孔包装膜开孔。当微孔直径为100 µm时，孔径足够小，O2分子和CO2分子在微孔中流动的阻力主要来源于气体分子同孔壁的碰撞，方可用Kundsen系数替代Fick定律中薄膜气体渗透系数m的方法建立开孔模型。以此判定模型3-1可以用于果蔬微孔包装膜开孔。

基于模型2-1计算得出的开孔方案（1孔15 µm）和基于模型2-2计算得出的开孔方案（1孔50 µm），均使包装袋的O2的体积分数维持在3%，CO2的体积分数维持在11%。其实测O2体积分数与预设O2体积分数不符，而实测CO2体积分数与预设CO2体积分数接近。这可能是因为当微孔直径太小时，由于O2分子的体积比CO2分子的体积要小，O2分子在通过微孔时其阻力主要源于O2分子同孔壁的碰撞摩擦，而CO2分子在通过微孔时其阻力部分源于气体分子间的碰撞摩擦，部分源于CO2分子同孔壁的摩擦。即当微孔直径足够小时（50 µm），只有CO2分子在微孔中的扩散情况符合黏性流动规律，适用Hagen-Pouiseville定律。以此判定模型2-1与模型2-2不适合用于果蔬微孔包装膜开孔。

表5 樱桃腐烂情况

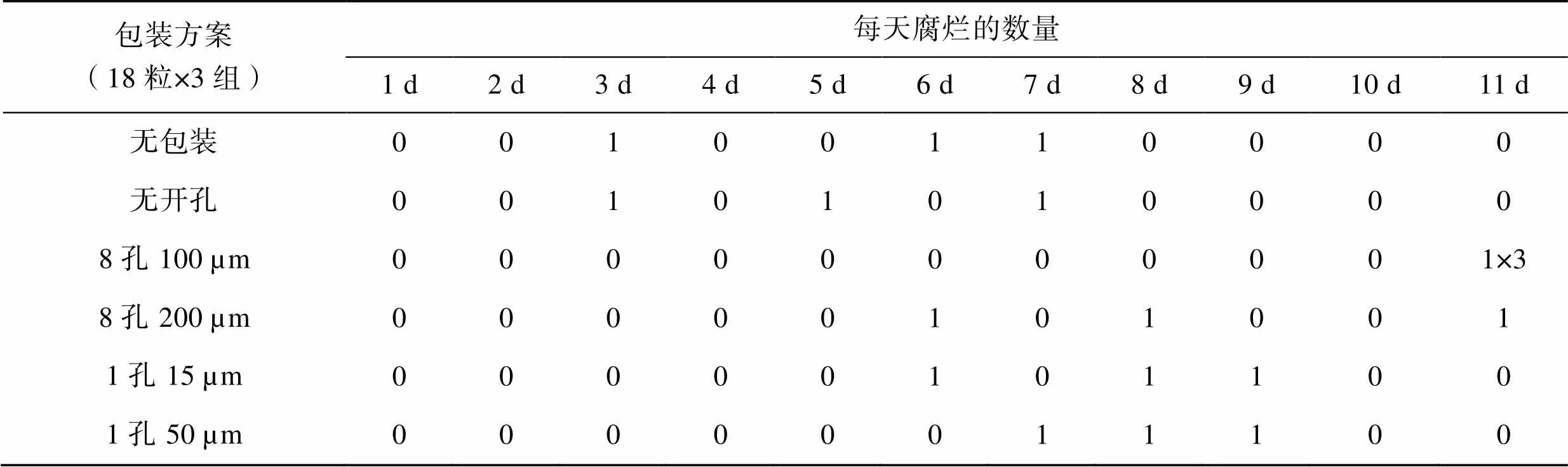
Tab.5 Decay of cherries

4 结语

模型1-1与模型1-2计算得出的微孔孔径过大，开孔数量太多，影响包装袋外观和机械强度，不适合用于果蔬微孔包装膜开孔。模型2-1的开孔方案，包装袋内实测O2浓度和CO2浓度与预设气体浓度不符，模型2-2设计的开孔方案，包装袋内实测O2浓度与预设O2浓度不符，只有实测CO2浓度与预设CO2浓度接近，因此判定模型2-1与模型2-2不适合用于果蔬微孔包装膜开孔。模型3-2的开孔方案，包装袋内实测O2浓度和CO2浓度与预设气体浓度不符，同样不适合用于果蔬微孔包装膜开孔。模型3-1的开孔方案，包装袋内实测O2浓度和CO2浓度与预设气体浓度最为接近，说明当微孔直径为100 µm时，可以将O2分子和CO2分子在微孔中的扩散状况近似看作气体分子在原膜中的扩散状况。故仅需将气体分子在原膜中的扩散系数换成Kundsen系数即可，即模型3-1可用于果蔬微孔包装膜开孔。

[1] OLIVEIRA M, ABADIAS M, USALL J, et al. Application of Modified Atmosphere Packaging as a Safety Approach to Fresh-Cut Fruits and Vegetables a Review[J]. Trends in Food Science & Technology, 2015, 46(1): 13-26.

[2] 张岩, 卢芳芳, 张海燕, 等. 果蔬自发气调包装中呼吸速率研究进展[J]. 食品安全质量检测学报, 2021, 12(18): 7105-7111.

ZHANG Yan, LU Fang-fang, ZHANG Hai-yan, et al. Research Progress on Respiratory Rate in Spontaneous Modified Atmosphere Packaging of Fruits and Vegetables[J]. Journal of Food Safety & Quality, 2021, 12(18): 7105-7111.

[3] BOONTHANAKORN J, DAUD W, AONTEE A, et al. Quality Preservation of Fresh-Cut Durian Cv. 'Monthong' Using Micro-Perforated PET/PE Films[J]. Food Packaging and Shelf Life, 2020, 23: 100452.

[4] 胡红艳. 微孔膜果蔬气调包装机理及其应用研究[D]. 无锡: 江南大学, 2007: 4-5.

HU Hong-yan. Study on Mechanism and Application of Modified Atmosphere Packaging for Fruits and Vegetables with Microporous Membrane[D]. Wuxi: Jiangnan University, 2007: 4-5.

[5] 李方, 卢立新. 微孔膜气调包装内外气体交换数学模型的建立[J]. 食品科学, 2010(4): 257-259.

LI Fang, LU Li-xin. Modeling of Gas Exchange in Modified Atmosphere Packaging with Perforated Film[J]. Food Science, 2010, 2(4): 257-258.

[6] MAHAJAN P V, OLIVEIRA F A R, MONTANEZ J C, et al. Development of User-Friendly Software for Design of Modified Atmosphere Packaging for Fresh and Fresh-Cut Produce[J]. Innovative Food Science & EmergingTechnologies, 2007, 8(1): 84-92.

[7] MASTROMATTEO M, CONTE A, PREVITALI M A, et al. Simplified Approach Based on Polynomial Equations to Predict the Permeability of Micro-Perforated Polymeric Films[J]. Packaging Technology and Science, 2016, 29(11): 549-558.

[8] LWIN H P, LEE J, LEE J. Perforated Modified Atmosphere Packaging Differentially Affects the Fruit Quality Attributes and Targeted Major Metabolites in Bell Pepper Cultivars Stored at Ambient Temperature[J]. Scientia Horticulturae, 2022, 301: 111131.

[9] 陈涛, 张国亮. 化工传递过程基础[M]. 3版. 北京: 化学工业出版社, 2009.

CHEN Tao, ZHANG Guo-liang. Fundamentals of Chemical Transfer Process[M]. 3rd ed. Beijing: Chemical Industry Press, 2009.

[10] 柯斯乐. 扩散流体系统中的传质[M]. 北京: 化学工业出版社, 2002: 111-116.

CUSSLER E L. Mass Transfer in Fluid Systems[M]. Beijing: Chemical Industry Press, 2002: 111-116.

[11] 王爱荣, 王跃, 唱桂凤. Maxwell-Stefan方程在多孔结构内传质方面的应用[J]. 山东理工大学学报(自然科学版), 2004, 18(3): 100-105.

WANG Ai-rong, WANG Yue, CHANG Gui-feng. Maxwell-Stefan Equation to Mass Transfer in Porous Structure[J]. Journal of Shandong University of Technology (Science and Technology), 2004, 18(3): 100-105.

[12] 傅献彩, 侯文华. 物理化学-下册[M]. 6版. 北京: 高等教育出版社, 2022: 22-24.

FU Xian-cai, HOU Wen-hua. Physical Chemistry-Volume II[M]. 6th ed. Beijing: Higher Education Press, 2022: 22-24.

[13] 侯玉茹, 王宝刚, 李文生, 等. 草莓呼吸特性与发酵阈值研究[J]. 保鲜与加工, 2019, 19(1): 25-31.

HOU Yu-ru, WANG Bao-gang, LI Wen-sheng, et al. Study on Respiratory Characteristics and Fermentation Threshold of Strawberry[J]. Storage and Process, 2019, 19(1): 25-31.

[14] LEE D S, HAGGAR P E, LEE J. Transient State In-Pack Respiration Rates of Mushroom under Modified Atmosphere Packaging Based on Enzyme Kinetics[J]. Journal of Food Science, 1991, 56(6): 1580-1585.

[15] HO P L, TRAN D T, HERTOG M L A T M, et al. Modelling Respiration Rate of Dragon Fruit as a Function of Gas Composition and Temperature[J]. Scientia Horticulturae, 2020, 263: 109138.

[16] WINOTAPUN C, ISSARASEREE Y, SIRIRUTBUNKAJAL P, et al. CO2Laser Perforated Biodegradable Films for Modified Atmosphere Packaging of Baby Corn[J]. Journal of Food Engineering, 2023, 341: 111356.

[17] RAI D R, PAUL S. Transient State In-Pack Respiration Rates of Mushroom under Modified Atmosphere Packaging Based on Enzyme Kinetics[J]. Biosystems Engineering, 2007, 98(3): 319-326.

[18] KANDASAMY P. Respiration Rate of Fruits and Vegetables for Modified Atmosphere Packaging: a Mathematical Approach[J].Journal of Postharvest Technology, 2022, 10(1): 88-102.

Establishment and Validation of Perforation Model for Fruit and Vegetable Microporous Packaging Film

YU Li1,2, LIN Yuan-zhi1,2*, WANG Yong-xiang3

(1. Fujian Polytechnic Normal University, Fujian Fuqing 350300, China; 2. Fujian Universities and Colleges Engineering Research Center of Soft Plastic Packaging Technology for Food, Fujian Fuqing 350300, China; 3. Forop Advanced Materials Co., Ltd., Fujian Fuqing 350399, China)

The work aims to develop a perforation model of microporous packaging films for fruits and vegetables, so that the gas concentration inside the bags could be accurately controlled to extend the shelf life of fruits and vegetables. By analyzing the gas permeability mechanism in the microporous films, and combining the original film permeability mechanism and the fruit and vegetable's own respiration rate, a perforation model of packaging films was established. And with cherries as the packaging object, the accuracy of the perforation model was judged by comparing the measured gas concentration in the packaging container with the predicted gas concentration. The internal measured oxygen concentration of the packaging scheme designed according to opening model 3-1 best matched the predicted oxygen concentration. For the package scheme designed according to model 1-1 and model 1-2, the hole diameter was as small as millimeter and the number of holes was as more as 100, it was not suitable for film perforation. The internal measured gas concentration of the packaging scheme designed according to model 3-2, model 2-1 and model 2-2 was not consistent with the predicted gas concentration. It is proved that the diameter of the microporous pores directly affects the diffusion pattern of gas molecules in the microporous pores and the accuracy of the perforation model. When the micropore diameter is 100 µm, the mathematical model constructed using Fick's law and the diffusion coefficient Dkcan accurately control the O2concentration and CO2concentration inside the bag. Microporous air-conditioned packaging bags based on this model can effectively extend the shelf life of cherries.

perforation models; microporous films; air permeability mechanism of film

TS255.36

A

1001-3563(2023)23-0111-07

10.19554/j.cnki.1001-3563.2023.23.013

2023-02-23

2021年度福建省中青年教师教育科研项目（科技类）（JAT210374）；食品软塑包装技术福建省高校工程研究中心2021年度开放基金项目（G1—KF2109）；横向课题（HX2022079，HX2022080，HX2022078）

责任编辑：曾钰婵