考虑冲突避免的多AGV路径规划研究

杨玮，杨思瑶，张子涵

考虑冲突避免的多AGV路径规划研究

杨玮，杨思瑶，张子涵

（陕西科技大学 机电工程学院，西安 710021）

提高物流企业“货到人”拣选系统在实际生产中的工作效率，避免自动导引小车（AGV）间的冲突死锁，研究大规模多AGV的无冲突路径规划和协同避障问题。首先考虑AGV空载、负载情况和路径扩展成本，改进A*算法，动态调整代价函数，优化路径扩展方式。其次，提出冲突检测及避免算法，对可能产生局部冲突的路径交叉点进行避障调度，通过预约锁格，实现局部冲突的检测，制定优先级避障策略，解决AGV动态行驶路径上产生的局部冲突和死锁，进而实现全局无冲突路径规划。对多组不同任务量和不同AGV规模的场景进行仿真，实验结果表明，考虑冲突避免的改进A*算法能有效实现100个任务、90个货架单位和7个拣选站场景下的多AGV动态路径规划，相较于传统A*算法，其平均拣选时长缩短了52.61%。该方法可实现大规模场景下的多AGV动态路径规划，在付出较小转弯代价的同时有效避免局部动态冲突，该方法可为相关企业实现多AGV协同调度提供新的思路和理论依据。

“货到人”拣选系统；自动导引小车；改进A*算法；冲突检测及避免算法；动态路径规划

随着电商行业的快速发展和人工智能技术的不断成熟，采用机器人代替人工作业已成为制造业及物流业发展的大趋势，越来越多的企业开始在生产车间应用移动机器人系统协助生产[1]。有报告显示[2-3]，全球已有超十万的多移动机器人系统和超百万的移动机器人被应用于物流的仓储环节。2008年，亚马逊公司首次在物流仓库使用了Kiva System，该系统是一种自动化程度较高的移动机器人履行系统（Robotic Mobile Fulfillment Systems，RMFS），通过多辆自动导引小车（Automated Guided Vehicle，AGV）合作进行货物的存储、搜索、选择和运送工作，完成仓储环节的作业[4]。传统物流仓库的拣货、补货等作业大多由人工完成，存在拣选时间长、拣选效率低等问题，无法满足现代物流快速、高效的发展需求[5]。与传统仓库“人到货”的拣选模式不同，RMFS系统通过中央控制系统集中控制AGV，实现了高效的“货到人”拣选作业，是一种典型的“货到人”拣选系统，多AGV合作作业取代了传统仓储系统中人工作业的方式，使得RMFS系统具有更高的拣货效率、更高的吞吐能力、更好的可扩展性和系统柔性[6]。随着现代物流设备的自动化和智能化发展，未来仓库的发展趋势必将是规模化和集约化。提高多AGV的集群化调度能力，尤其是针对较大规模的多AGV路径规划，是仓储系统自动化与智能化发展中必须克服和突破的技术难点，也是影响企业物流效率的重要因素[7]。

路径规划是移动机器人搬运作业中的关键问题之一，根据路径规划目标和规划路径时系统环境状态的不同，可以将移动机器人的路径规划问题划分为GPP和LPP[8]，即移动机器人的全局路径规划和局部路径规划[9]，文中综合考虑GPP和LPP研究“货到人”拣选系统的路径规划问题。目前，多AGV路径规划的研究内容主要集中在数学方法、仿真研究和智能算法方面，以“货到人”拣选系统等智能物流系统为背景的研究较少涉及AGV数量和任务量，且对动态实时性问题考虑不足[10]。由于仓库中大规模机器人集群调度的问题较复杂，是动态、多目标的，已被证明是NP难问题[11]，因此对于移动机器人路径规划问题的研究仍是探索移动机器人控制领域的重要方向[12]。传统的AGV路径规划是为AGV规划出一条到达目标点的无碰撞最短路径，一般利用可视图、Voronoi 图、栅格图、人工势场等路径规划方法[13]，并通过深度优先算法、广度优先算法[5]、Dijkstra算法、A*算法或 D*算法等求解[14]。刘生伟等[15]剔除了寻路过程中的冗余节点，进而改进A*算法，其寻优效果好，但其中涉及的机器人数量较少。Duchon等[16]提出一种改进的A*算法，通过修改代价函数，为个别场景下的路径规划提供参考，但其涉及的AGV数量较少。李伟光等[17]提出了一种考虑转弯因素的改进A*算法，但未考虑AGV规模大量增加时其算法的路径搜索效率。Singh等[18]考虑了安全距离，采用改进的 A*算法进行路径规划，有效避免了冲突，提高了系统的整体效率。牟德君等[19]以总工作时间最短为目标，改进了A*算法代价函数计算公式，提出了一种适用于仓储环境的改进A*算法。Ren等[20]提出了一种基于特征图的全局路径规划算法，使得优化后的路线更短且更平稳。Zhong等[21]提出了一种混合路径规划方法，用于解决大规模动态环境下移动机器人的全局路径规划、实时监测和避障等问题。Wang等[22]以路径最短为目标进行了全局路径规划，确定了由初始点到参考直线的最佳切线弧路径。

虽然上述学者的研究取得了一定的效果，但在大规模AGV仓储系统中，多AGV共同作业时的冲突和碰撞次数将呈指数增加，导致规划的局限性。鉴于此，笔者在前人研究的基础上，进一步优化路径规划算法，综合研究了转弯因素、路径扩展成本、冲突避免等，实现了“货到人”拣选系统的全局无碰撞路径规划，提高了系统分拣效率，并通过仿真软件验证了文中所提路径规划算法的优越性。

1 考虑冲突避免的路径规划算法

A*算法是由Peter H等设计的一种启发式搜寻路径方法，结合了Dijkstra算法和快速随机搜索树算法[23]，利用等代价搜索和启发式搜索有效地计算出最优路径，计算出最佳优先搜索，具有搜索路径时间短[18]、鲁棒性好、运行速度快等优点。A*算法的核心在于不断更新OpenList和CloseList，通过选取OpenList中代价最小的节点作为优先级最高的节点进行扩展，在OpenList中存放待扩展节点，在CloseList中存放已扩展节点，当目标节点出现在CloseList中时，路径搜索结束，并回溯至父节点，得到路径。

A*算法见式（1），式中，()表示从初始节点到当前节点的总代价值，()表示从初始节点到当前节点的实际代价值，()表示从当前节点到目标节点的估计代价值。采用曼哈顿距离表达式计算估计代价值，见式（2）。式中，(,)表示节点与节点之间的曼哈顿距离，X表示目标节点的横坐标，Y表示目标节点的纵坐标，X表示当前节点的横坐标，Y表示当前节点的纵坐标。()的启发式函数可用式（3）表示，其中为AGV直线行驶1个栅格的代价，表示当前节点，表示目标节点。

()=()+() (1)

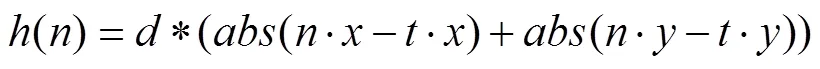
1.1 A*算法

1.1.1 问题描述

当系统中存在较大规模的AGV同时运行时，受到A*算法路径搜索机制的影响，在AGV行驶路径上可能存在较多的转弯节点，A*算法不能保证在解决多AGV碰撞和冲突的同时仍能搜寻到最优路径，且在转弯过程中AGV的单位耗电量将大大增加，因而会浪费系统资源[5]。此外，在仓库环境中一般将通道设置为双向单车道，AGV在空载时允许在无任务的可移动货架下方穿行，AGV在负载时仅允许在预设行驶规则的可通行巷道上通行，如图1～2所示。将货架、在驻点停留的AGV、载有可移动货架并在存储区执行任务的AGV分别视为静态和动态的障碍物，不同行驶方向的AGV可能在行驶路径的部分区域发生冲突，从而影响彼此通行，降低系统效率。

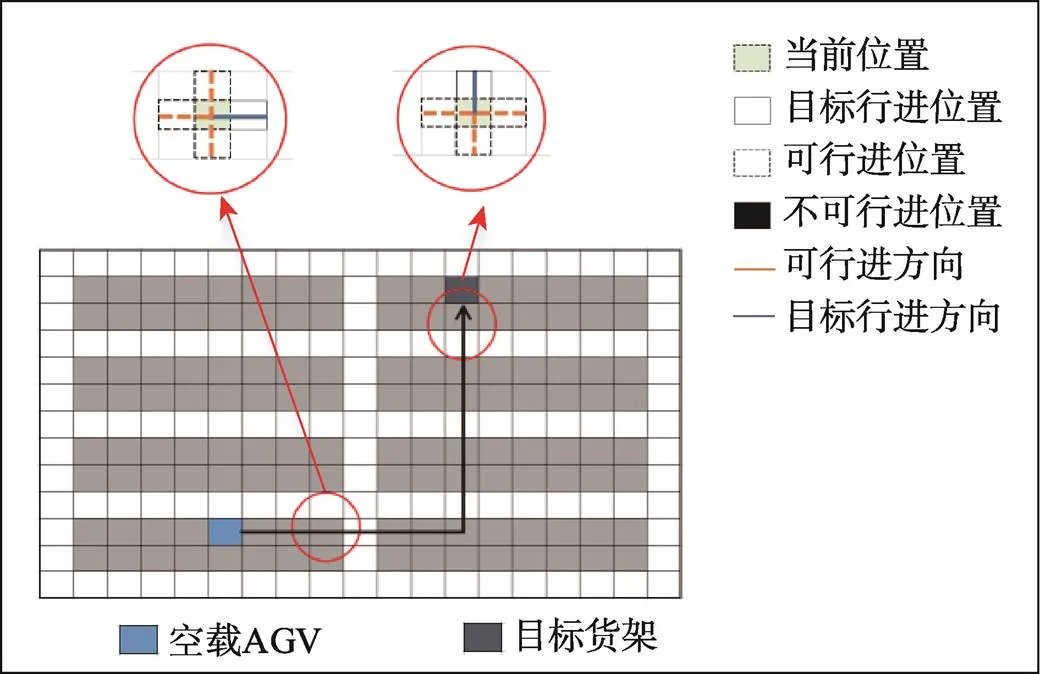
图1 空载AGV可通行路径情况

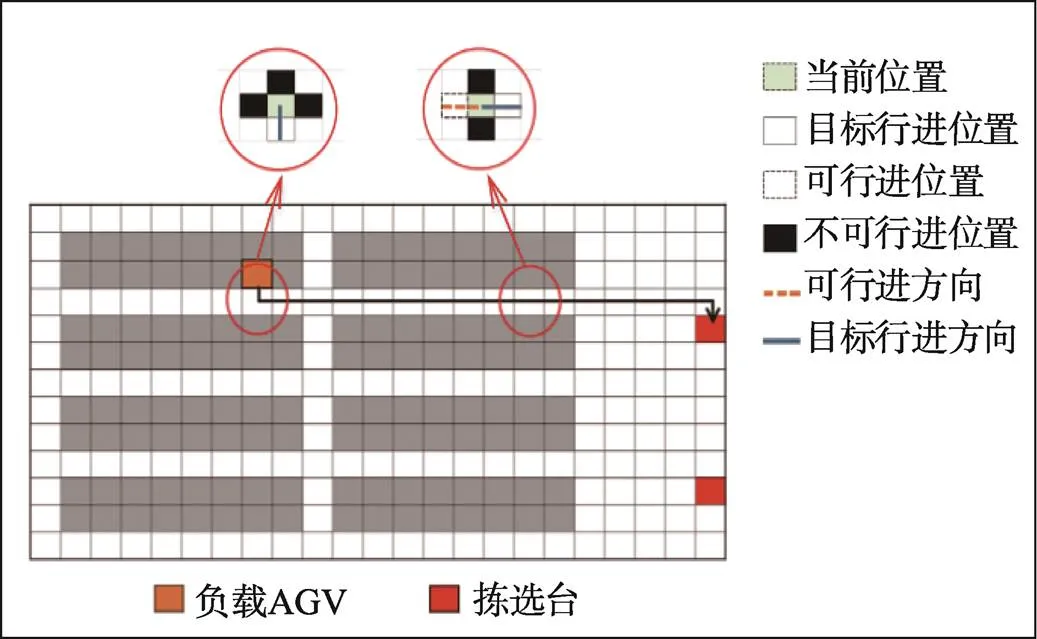
图2 负载AGV可通行路径情况

基于上述分析，在研究多AGV全局路径规划问题时，重点考虑以下3个问题：AGV负载和空载的不同行驶方式；减少AGV转弯次数，降低转弯成本；避免冲突，减少碰撞次数。研究目的在于提高“货到人”拣选系统中多AGV最优路径的搜寻效率和可靠性，解决多AGV间的冲突问题。

1.1.2 改进A*算法

A*算法总代价()主要取决于()和()的变化，在搜寻初期受其影响较大，算法的运行速度快、效率高。随着搜寻进程的变化，实际行走代价()逐渐增大，而估算代价()逐渐减小，()受启发式搜索的影响变小，算法需要搜寻更多节点才能完成搜寻目标，搜寻效率降低。为了稳定路径规划算法的性能，首先对实际代价()和估算代价()设置权重，动态调整它们在算法搜寻进程中的影响。设置动态调整权重后的总代价()，见式（4）。其中，AGV的当前起始位置为(x,y)，目标节点位置为(goal,goal)，中间节点位置为(x,y)，分别将起始位置、目标位置与中间位置曼哈顿距离的比值作为实际代价和估算代价的动态权重。

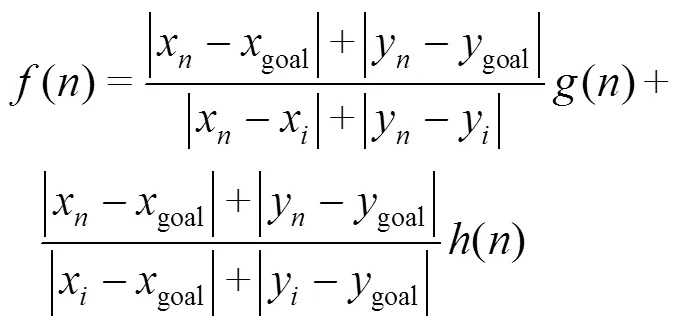
为了避免搜寻路径上出现转弯次数过多的情况，进一步将转弯代价加入代价函数中进行考虑。若AGV的当前位置为(x,y)，那么与其对应的父节点为(x–1,y–1)，子节点为(x+1,y+1)。可利用节点信息判定转弯，当(x,y)–(x–1,y–1)与(x+1,y+1)–(x,y)相等时，表示AGV向下一节点移动时未发生转弯动作，否则表示AGV在节点(x,y)发生转弯动作；AGV移动1个栅格的基础代价为，设置转弯惩罚因子为。当判定发生转弯时，为1，否则为0，则转弯惩罚代价可表示为式（5）。改进A*算法的代价函数表达见式（6），具体步骤如下。

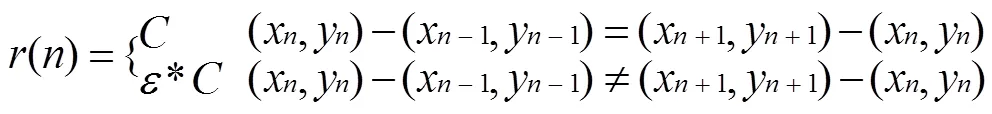
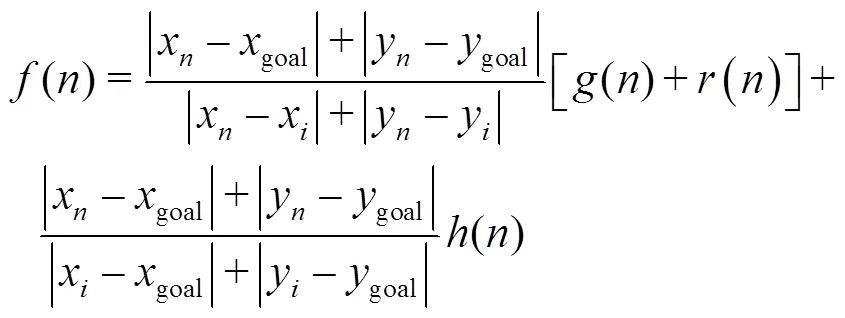
1）确定AGV空载和负载状态时的系统搜索地图MAP1、MAP2，将路径规划分为3个阶段，在3个阶段内分别以MAP1、MAP2、MAP2的顺序进行路径搜索。

2）输入AGV的起始点、中间节点、目标点，需要寻找的3段最短路径为→，→，→，标记为P1、P2和P3。

3）构建OpenList和CloseList存储节点位置信息，将起始点插入OpenList，同时置空CloseList；再将起始点插入CloseList，循环规划3段路径。

4）判断OpenList是否为空，若是，搜索路径失败；否则以OpenList中改进的评价函数()最小的节点作为当前节点，检查其周围4个邻接节点，并计算()。

5）判断()最小的邻接节点'是否为障碍物，若是，则放弃该节点；否则计算该节点的'()。若'()<()，则将其放入OpenList，并更新()。

6）循环Step 4至Step 5，直至输出最短路径P1。

7）最短路径P2、P3的搜索流程同上，移动机器人执行任务的最短路径为3段路径的长度和。

1.2 冲突检测及避免算法

为了满足路径规划可通达性的要求，首先采用改进A*算法对已知分配结果的货架及AGV进行初步静态路径规划。根据任务执行时间的优先级设置二维预约表，并通过预约锁格方法进行局部冲突检测，随后设计优先级避障策略，解决局部冲突，最终完成全局无冲突路径规划。为了便于研究，对以下条件进行假设。

1）在同一时刻内，1个栅格仅能被1辆AGV占用，1辆AGV不能同时占用2个及以上的栅格。

2）在AGV接收到拣选任务时，已知该任务的起始点和目标点位置。

3）不考虑AGV行进过程中的变速，设置其匀速通过每个栅格，通过1个栅格的时间为1 s。

4）已知仓库中可移动货架、充电站和拣选台的位置，动态障碍物仅包括在仓库中行驶的其他AGV，且所有AGV的运动信息已知。

取大鼠脑组织（处死前已注射FITC-D）置于4%多聚甲醛溶液中固定24 h后，常规脱水、石蜡包埋、切片（5 μm），参照Weidner法[21]测定大鼠脑组织梗死区域的MVD。寻找梗死区域内5个血管密集区，于200倍荧光倒置显微镜下计算该区域内被染成绿色的微血管数目。每份切片均选取5个高倍视野计数，取其平均值。

5）设置通道为双向单车道，AGV可以在巷道内沿着路径方向自由行驶。

多台AGV同时执行任务，不可避免地会发生路径冲突。为了有效解决AGV在行走过程中可能出现的碰撞和死锁问题，主要针对AGV行驶过程中可能出现的交叉点冲突、对向冲突、追击冲突和连续冲突提出相应的冲突解决策略，并进行局部路径规划，冲突示意图如图3所示。

1.2.1 预约锁格

预约锁格的核心是在AGV移动过程中不断检查路径上栅格节点的占用情况，为优先级高的AGV连续提前锁定一段安全距离，在安全距离内保障当前AGV的无障碍通行，并更新预约表，直至所有任务完成。预约表锁定的安全距离随着AGV移动位置的变化而改变，安全距离的长度由锁格范围决定。不同的锁格范围会影响AGV在系统中的等待时间，锁格范围过长会影响路径规划的效率[24]。由此可见，只有确定AGV当前位置、任务起始位置，并设置好锁格范围后，才能确定在预约锁格策略下的AGV运行路线。如图4所示，已知AGV1和AGV2的任务起始节点和终点，若将锁格范围设置为2，则系统始终在到+2时刻内将每辆AGV锁定接下来的2个栅格单元作为安全行驶范围，已被AGV1锁定的栅格单元不能同时被其他AGV锁定。

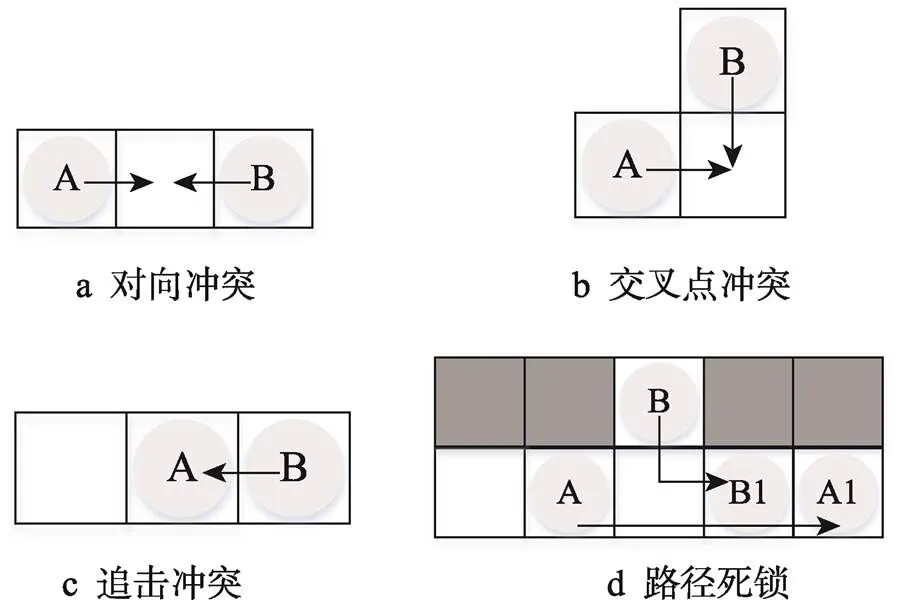
图3 不同冲突类型

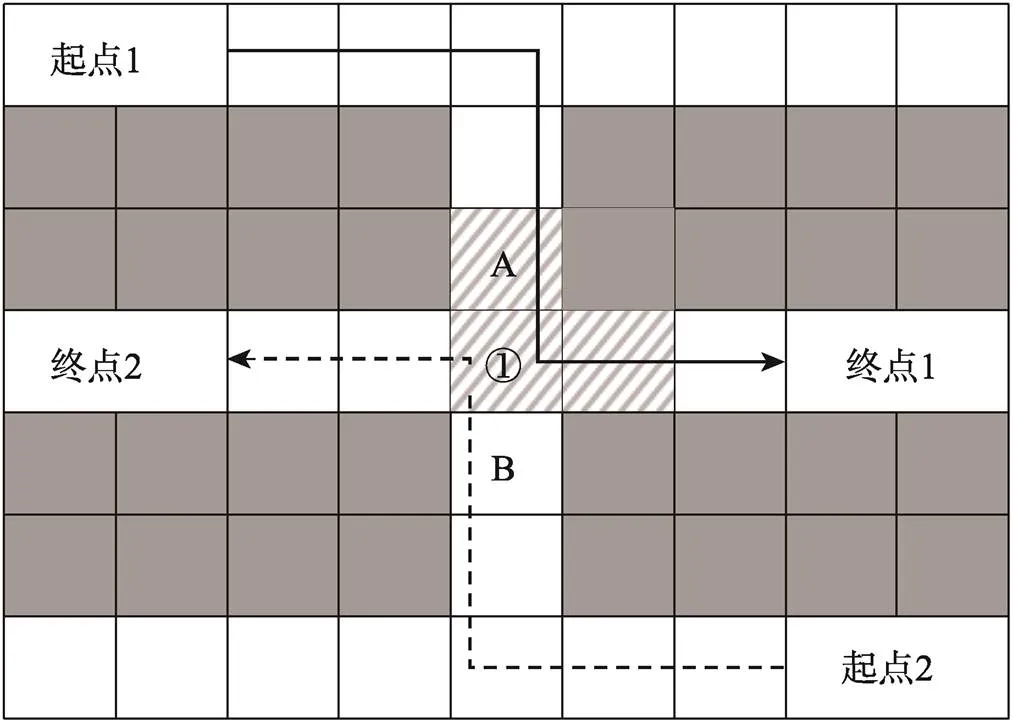
图4 预约锁格

1.2.2 优先级避障策略

1）节点等待。在AGV执行任务过程中，预约表检测到同一时刻内下一锁格范围内即将发生的冲突，则使优先级低的AGV在当前节点等待一个安全的时间间隔后再出发。

2）重新规划。在AGV执行任务过程中，等待时间过长或与其他AGV形成死锁时，对死锁环上优先级低的AGV重新规划路径，优先级高的AGV按原规划继续通行，然后依次调度其他优先级低的AGV。

3）组合策略。AGV已经采用某一策略进行路径规划时，由于实际运行时系统中存在大规模AGV同时执行任务，且可能存在再次冲突的情况，因此通过多个避障策略组合进行避免。

综上所述，考虑冲突避免的改进A*算法（Improved A*algorithm considering conflict avoidance，IPA*-CA）搜寻全局无冲突路径的过程如图5所示，步骤如下。

1）系统接收实时任务后，采用栅格法对地图进行编号，定位AGV、货架和拣选台的位置。

2）调用改进A*算法进行初步路径规划，获取静态障碍下的临时路径。

3）根据任务列表中的执行时间和初始行驶路径构建二维预约表，对每辆AGV执行目标货架的起始时间设置安全时间间隔，降低初始规划时AGV拥堵的可能性，AGV按照更新后的预约表执行拣选任务。

4）启用预约锁格策略。始终为每辆AGV锁定一段栅格节点作为安全距离，以确保其顺利通行。当某辆AGV路径确定后，其他AGV经过预约表查询相继锁定路径并完成任务。

5）不断获取占用点信息，判断安全距离内是否会发生冲突。若发生冲突，则即刻启用优先级避障策略，在决策AGV通行顺序的同时解决冲突，否则进入下一步骤。

6）判断所有目标货架的拣选路径是否均已检测。若是，则更新预约表，并执行下一步骤，否则继续检测，并执行步骤4）。

7）当前所有AGV完成拣选任务后，判断任务列表是否已为空。若列表已空，则规划结束，否则重复步骤2）～6），直至所有任务结束。

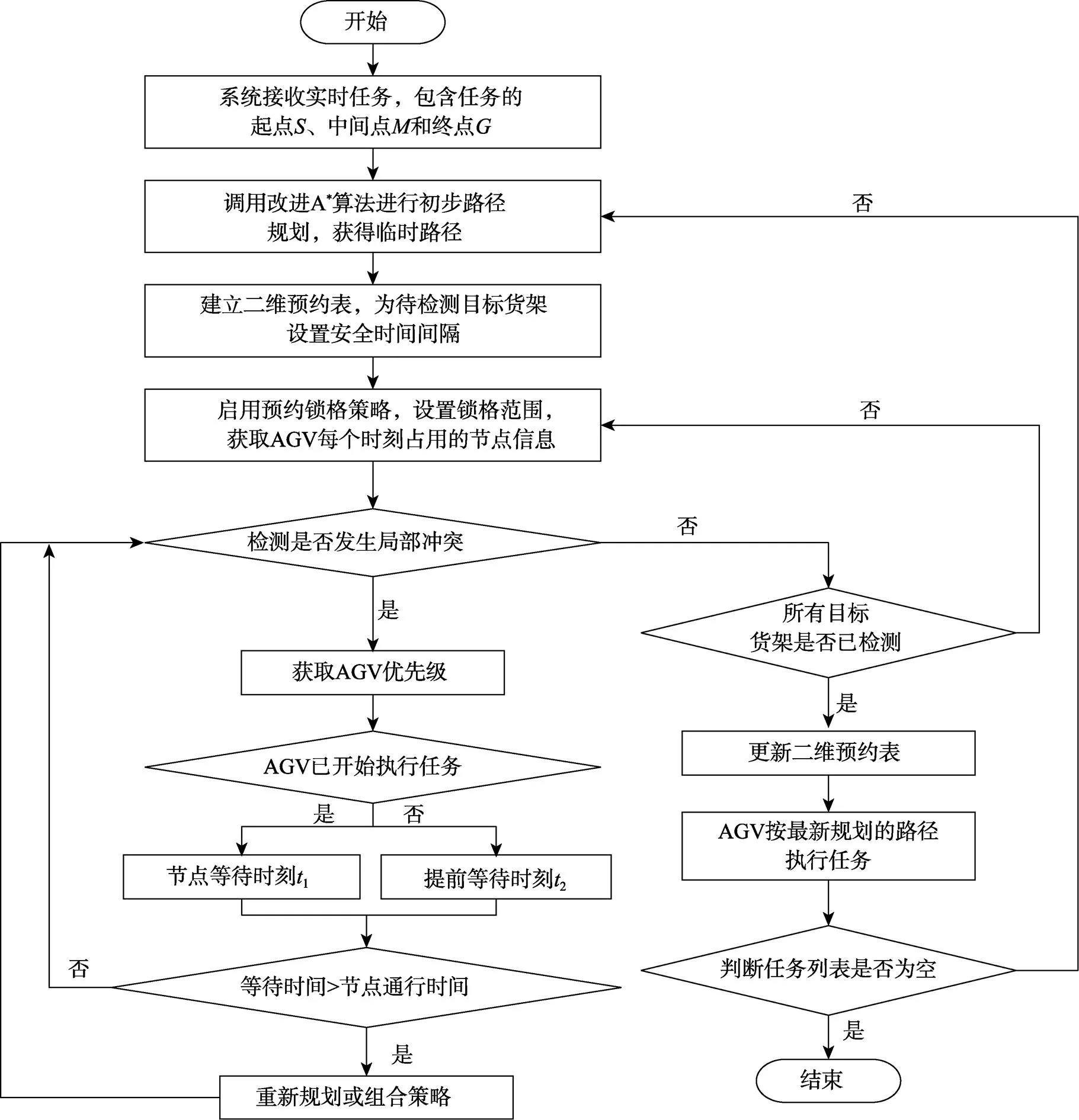
图5 考虑冲突避免的路径规划算法

2 结果与分析

2.1 小规模仿真实验分析

为了讨论所提IPA*-CA算法搜寻路径的有效性，基于Matlab 2022b设置1组小规模实验进行研究。采用栅格法建立小规模环境模型，生成3项调度安排，包括2个拣选站、3台AGV和3项拣选任务，AGV起始驻留位置、目标货架位置、拣选台位置及各项任务的起始时刻如表1所示，设置每辆AGV的行驶速度为1 m/s，栅格尺寸为1 m×1 m。分别采用A*算法、ACO算法和IPA*-CA算法进行多AGV路径规划实验。

表1 实验基本设置

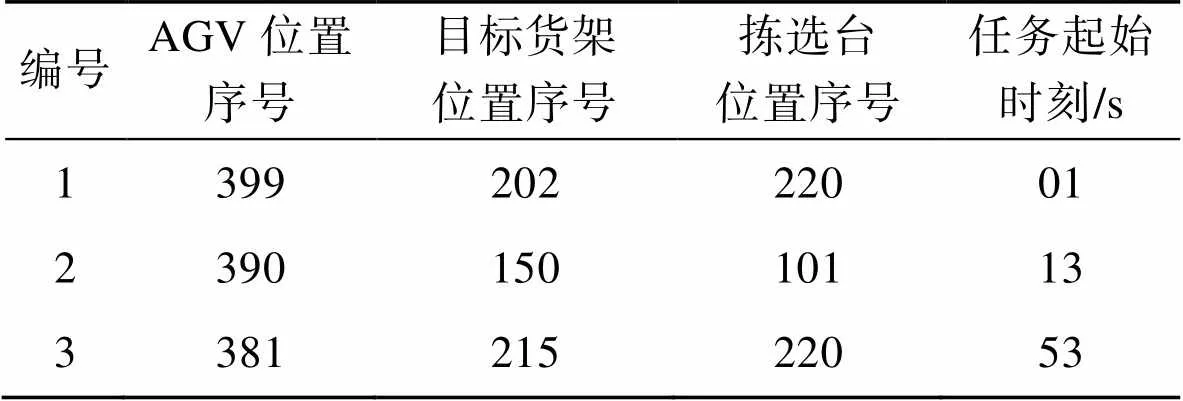
Tab.1 Basic experimental settings

如图6所示，分别使用3种算法规划出多AGV行驶路径，重复实验10次，3种算法在路径长度和转弯次数方面的表现如表2所示。实验结果表明，相较于A*算法和ACO算法，文中所提算法能有效提高路径搜索效率，并保持路径质量，AGV空载可穿行于货架下方的策略和动态调整A*算法代价函数的操作，使得规划的路径总长度更短、转弯次数更少。为了讨论IPA*-CA算法的动态避障效果，参考Bolu等[24]对多机器人路径规划的研究，设置锁格范围为2，采用文中所提算法进行避障实验。AGV路径规划结果如表3所示。节点通行顺序为3辆AGV通过各个节点的先后顺序，未调用避障算法时规划的临时路径，如图7所示。由图6c和图7a可知，AGV1与AGV2在节点190处的位置发生重叠，说明2辆AGV在相同时间范围内需要锁定同一资源点，在路径上发生了冲突。由图6c和图7b可知，AGV1与AGV3交换了在节点185和186处的位置，说明2辆AGV在相同时间范围内需要锁定对方资源点，在路径上发生了冲突。

调用冲突检测及避免算法，并完整运行所提算法后，获得了多AGV运行的实际路径。由于AGV1最早开始执行任务且与其他AGV发生冲突时均为负载状态，因此总是具有最高优先级。由图8a可以观察到，AGV1与AGV2冲突时，二者分别位于节点191和节点211处，由于AGV1的优先级较高，且设置的锁格范围为2，因而AGV1先占用了节点190和189，AGV2在节点211处等待2 s后继续执行任务，避免了冲突1。由图8b可以观察到，AGV1与AGV3冲突时，二者分别位于节点184和节点215处，由于AGV1的优先级较高，且设置的锁格范围为2，因而AGV1先占用了节点185和186，AGV2在节点211处等待4 s后继续执行任务，避免了冲突2。由图8c可知，3辆AGV在执行任务的全过程中不再出现相同时间范围内锁定同一资源点或对方资源点的情况，执行任务的总时长分别为87、76、72 s，行驶的路径总长度分别为51、36、30 m。由此可见，文中所提算法对避免多AGV冲突问题有效。

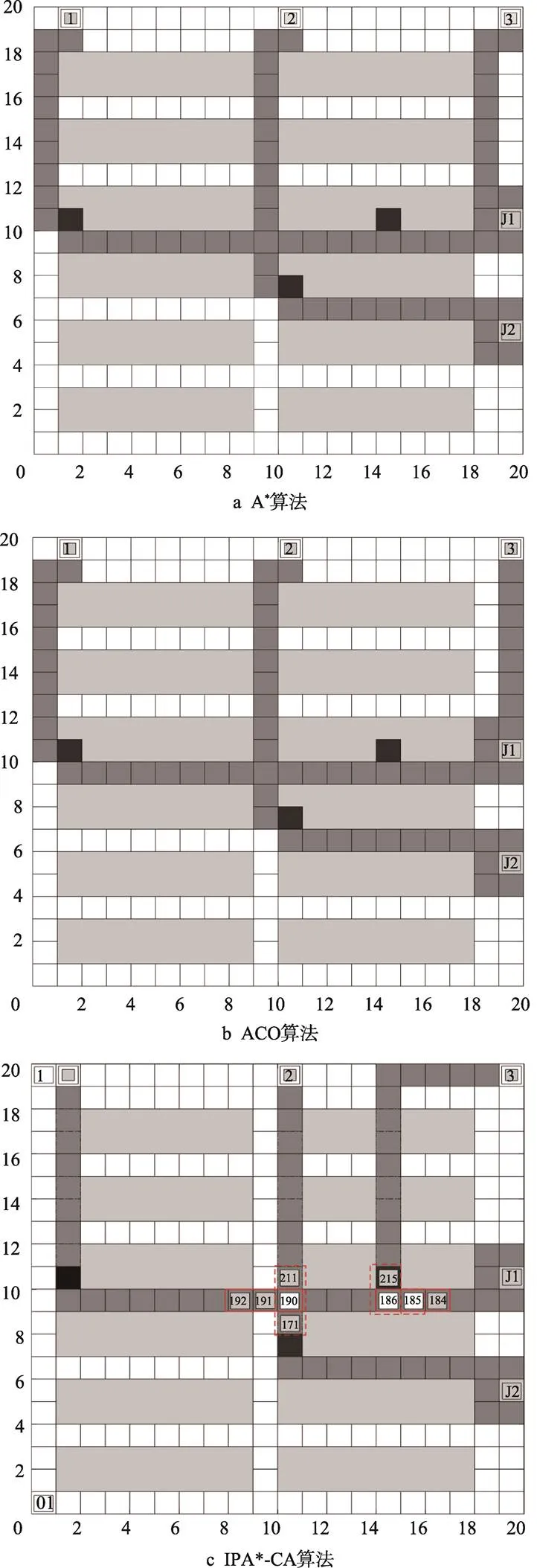
图6 3种算法的路径规划结果

表2 算法有效性实验

Tab.2 Algorithm effectiveness experiment

表3 避障实验结果

Tab.3 Results of obstacle avoidance experiment

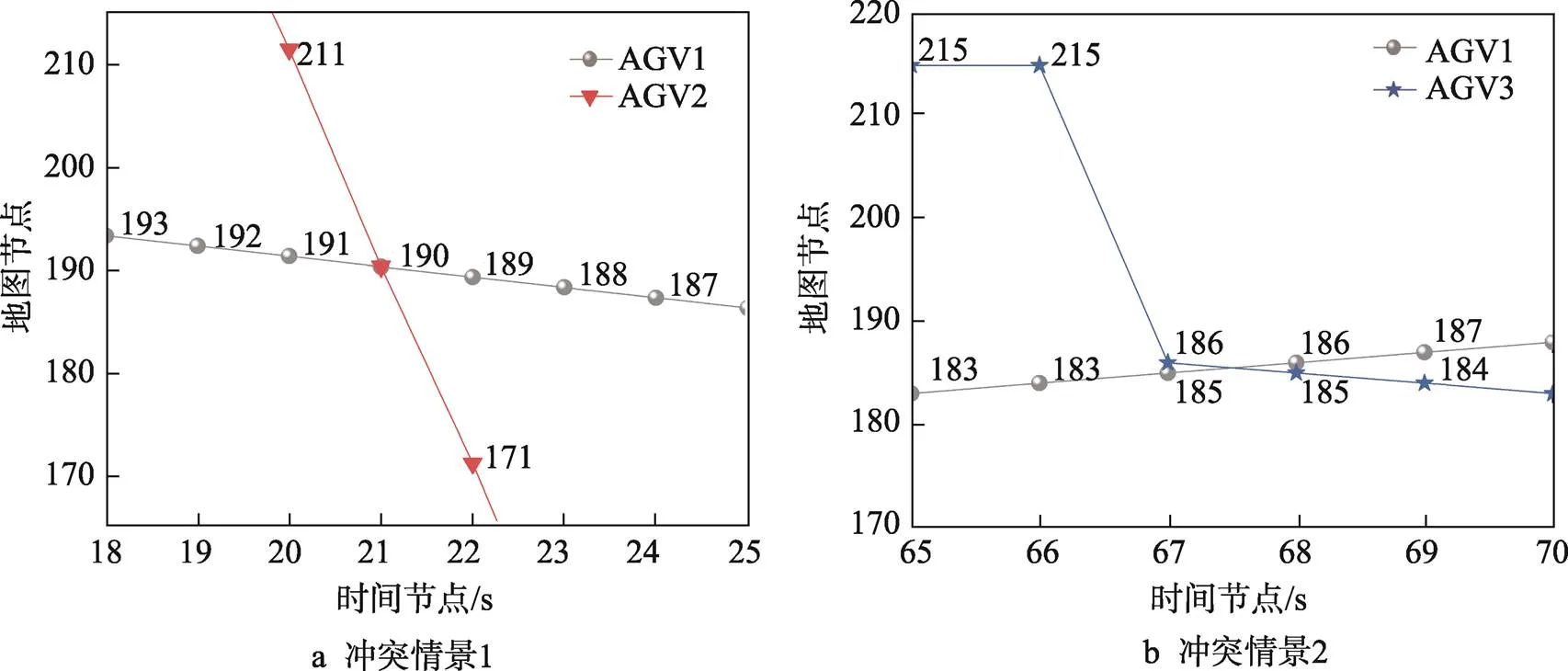
图7 存在冲突的初始路径

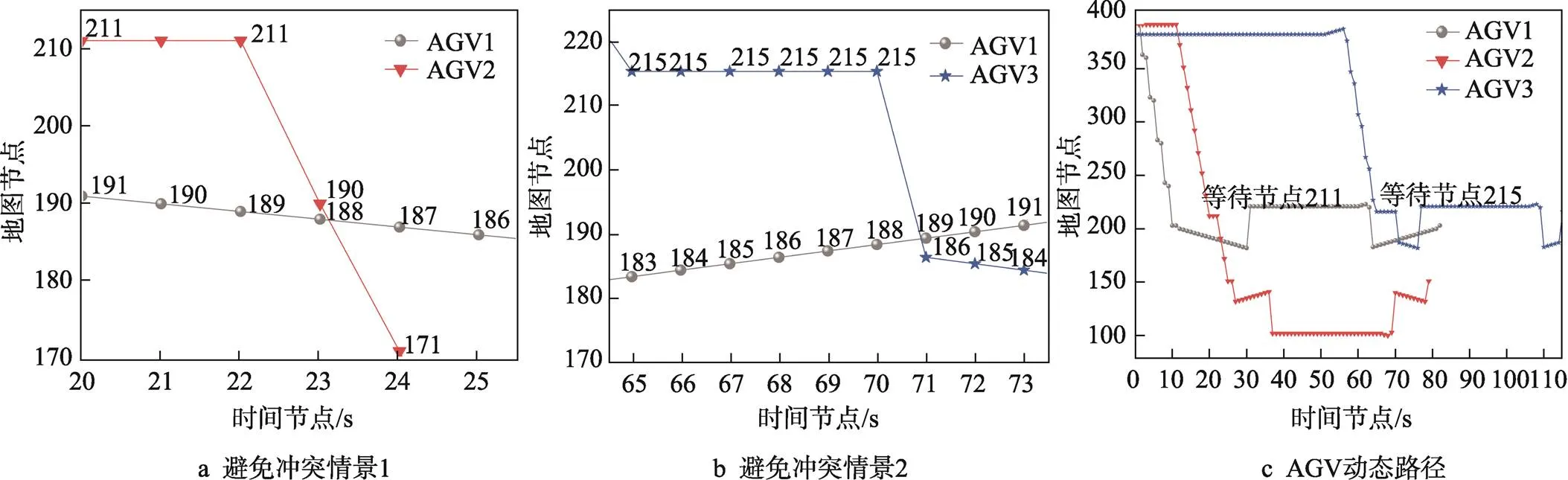
图8 避免动态冲突后的实际路径

2.2 大规模仿真实验分析

为了讨论所提算法的优化效果，设置实验基本参数，基于Flexsim仿真软件建立一个货架排列方式为2×8、布局为5列18排、共计90个货架单位和7个拣选站的仓库模型。在实验中，AGV随机驻留的货架位置为初始位置，订单任务随机生成并就近分配，设置AGV的行驶速度为1 m/s，栅格尺寸为1 m×1 m，将AGV每次转弯、抬起和放下货架的时间均设置为1 s，拣选每个货架的平均时间为30 s。系统中AGV需要经历3个阶段，分别为AGV前往目标点驮运货架、AGV将可移动货架驮至拣选台、AGV将可移动货架放回原存储位置。为了方便研究，下文统称考虑冲突避免的改进A*算法为算法1，A*算法为算法2，分别采用2种算法对不同实验参数下的模型进行仿真，进而研究所提算法在“货到人”拣选系统中的应用效果。

统计固定使用10辆AGV并改变系统任务量从20至200个时的仿真结果（表4），GAP值表示算法1与算法2平均拣选1个任务的时间差异度。通过比较结果可知，当系统中可用的AGV数量固定时，在2种算法下，AGV的转弯次数、系统中出现局部冲突的次数和完成拣选任务的总时长均随着拣选任务量的增加而增大，其原因是每辆AGV在同一时间段内仅能处理1项任务，任务量的累加使得系统内部更加复杂，AGV必须通过更高频次的工作才能完成所有任务，在等待和处理冲突过程中产生了时间损耗，并增加了冲突的可能性。

执行算法1和算法2时，路径上的转弯次数对比结果如图9a所示。相较于算法2，算法1规划的路径始终具有更少的转弯次数，随着任务量的增加，2种算法在规划路径转弯次数方面的差异更加明显。执行算法1和算法2时，路径上产生的局部冲突次数对比情况如图9b所示。算法1相较于算法2，产生的冲突始终更少，当任务量为20～80个时，2种算法下产生的冲突次数差距较小，当任务量超过100个后，算法1中产生的冲突次数缓慢增加，而算法2的冲突次数急剧增加，两者之间的差距快速增大。出现上述实验结果的原因是，在较少任务量下，AGV分配到的任务较平均，系统中发生冲突的频率较低，随着任务量的增大，AGV的工作频率明显增大，系统中相遇的可能性随之增加。当发生冲突时，算法2无法快速解决冲突，使得系统出现大量拥堵现象，而算法1则通过冲突预检测、优先级避障和预约锁格等操作避免了大量冲突，缓解了系统的拥堵情况。执行算法1和算法2时，AGV完成所有任务的拣选总时长对比情况如图9c所示。算法1的平均拣选时长为43.01 s/个，算法2的平均拣选时长为90.75 s/个，与算法2相比，算法1始终具有更快的拣选完成时间。说明当AGV在行驶中遇到动态的局部冲突或死锁等突发事件时，算法1能快速解决问题，并节约了大量时间资源。相较于算法2，算法1的平均拣选时间优化率为52.61%，优化效果明显。

表4 大规模任务量实验结果

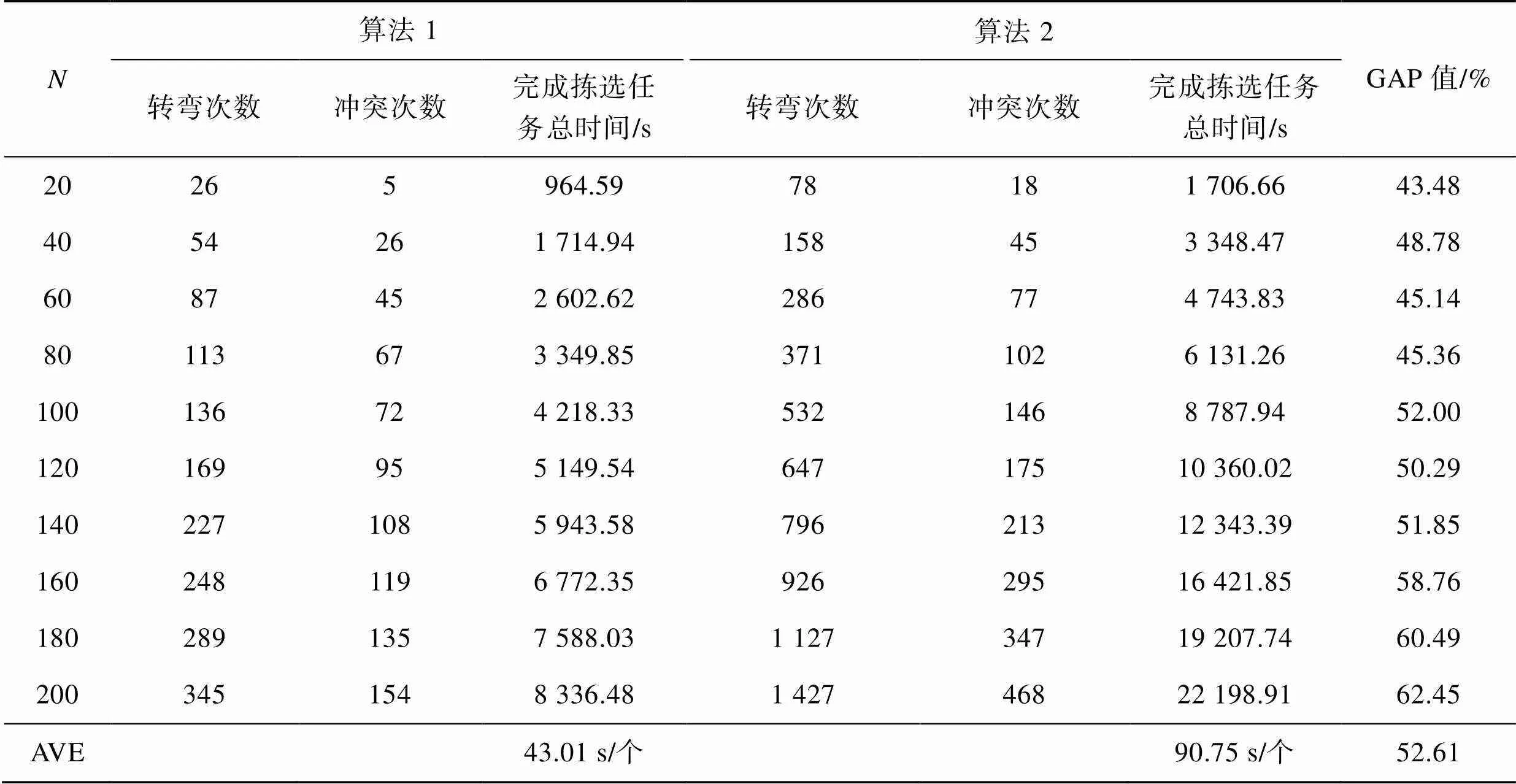
Tab.4 Results of large-scale task experiments

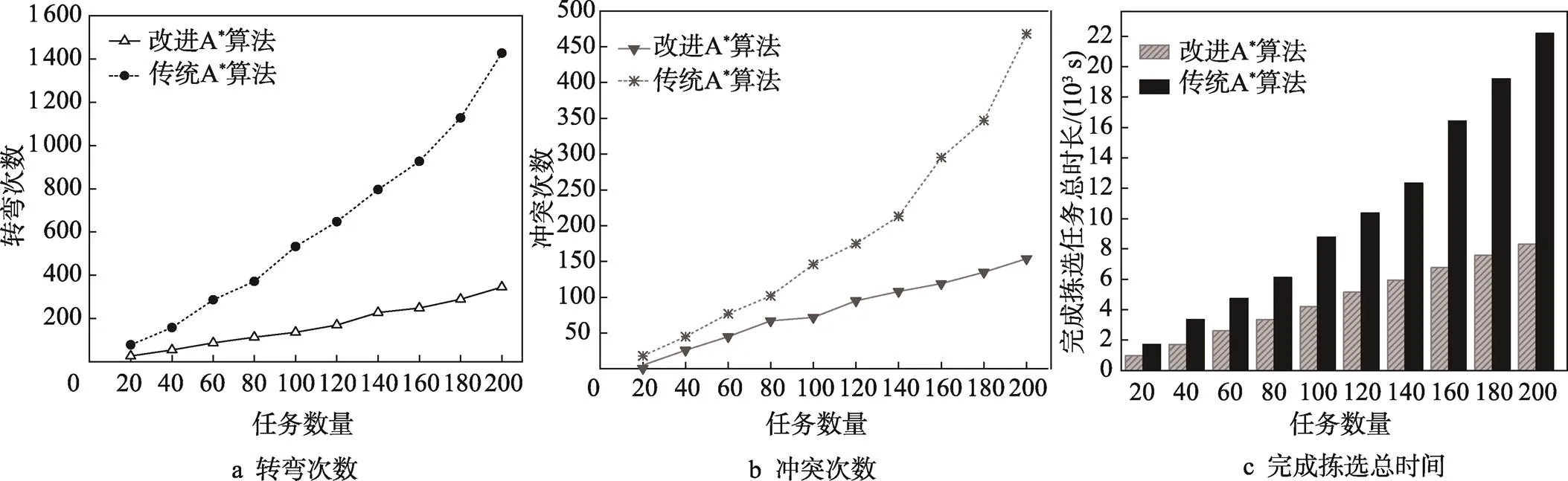
图9 不同算法的规划结果对比

统计固定系统任务量为100、改变AGV规模从5～30个的仿真结果如表5所示。将AGV行驶总路程、完成所有拣选任务的总时间作为衡量指标，讨论文中所提算法在不同AGV规模下的表现。当任务量固定时，随着AGV数量的增加，系统完成拣选任务的总时长逐渐缩短，而AGV行驶的总路程呈现先减少后增加的趋势。出现此现象的原因是，随着AGV规模的增加，系统的整体工作效率得到提高，但逐渐饱和的AGV容量增加了系统负荷，导致系统中出现了更多的局部冲突，算法1为了避免冲突而牺牲了部分路径成本。实验结果表明，算法1能有效地在不同系统规模下规划路径，但系统中AGV的数量并不是越多越好。在当前仓库规模下配置15辆AGV时，AGV行驶的总路程和完成拣选的总时长均较短，能获得更好的使用效果。

表5 不同AGV规模的仿真结果

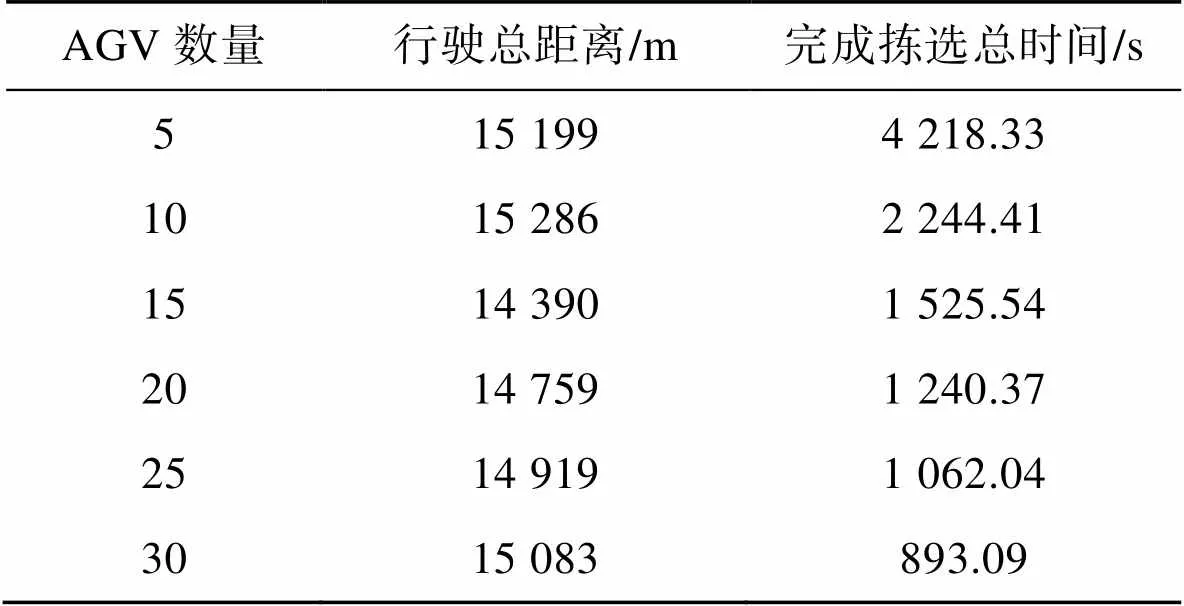
Tab.5 Simulation results under different scales of AGVs

综上所述，考虑冲突避免的改进A*算法在多AGV调度问题中的效果较好，尤其是系统中存在一定规模的待处理任务量和AGV时其效果更加突出。文中所提方法能够为物流仓库或制造业生产车间的调度提供思路。由于不同的系统环境存在差异，因此相关企业在配置仓库设备时，需要综合考虑仓库布局、拣选需求和系统容量，更好地对AGV规模进行决策。当AGV规模超过系统饱和状态所需的AGV数量时，系统整体能耗将随之增加，系统工作效率将受到影响，造成企业资源浪费。

3 结语

针对“货到人”拣选系统多AGV的路径规划和冲突避免问题进行了研究，提出了一种考虑冲突检测及避免的路径规划算法。首先考虑AGV空载、负载的不同状态，调整其行驶方式，对路径转弯成本设置惩罚因子，动态调整A*算法代价函数，改进A*算法，以优化AGV执行任务时的转弯次数。其次，设计冲突检测及避免算法，为满足路径规划的可通达性要求，提出了预约锁格策略，通过不断获取占用的节点信息，锁定安全距离，进而始终保障优先级高的AGV率先结束任务。针对系统中出现的局部动态冲突问题，提出了节点等待和重新规划等优先级避障策略，解决了局部动态冲突，进而获得了高效、可行的全局无碰撞路径。最后，基于仿真软件，通过多组不同任务量和不同AGV规模的仿真实验证明，文中所提的路径规划算法能有效避免系统中的冲突，并付出了较少的转弯代价。该算法在提高路径搜索效率的同时，能够保证搜索质量，具有较好的鲁棒性和实用性，能实现100个任务、90个货架单位和7个拣选站场景下的多AGV动态路径规划，能为企业采用“货到人”拣选系统促进仓库实际生产提供参考。

[1] CHEN Hai-long, WANG Qiang, YU Meng, et al. Path Planning for Multi-Robot Systems in Intelligent Warehouse[C]// International Conference on Internet and Distributed Computing Systems. Cham: Springer, 2018: 148-159.

[2] 本刊编辑部. 国际机器人联合会2021年全球工业机器人统计数据[J]. 机器人技术与应用, 2022(1): 47-48.

Editorial Department. The International Federation of Robotics 2021 Global Industrial Robot Statistics[J]. Robot Technique and Application, 2022(1): 47-48.

[3] RIZK Y, AWAD M, TUNSTEL E W. Cooperative Heterogeneous Multi-Robot Systems[J]. ACM Computing Surveys, 2020, 52(2): 1-31.

[4] ROY D, NIGAM S, DE KOSTER R, et al. Robot-Storage Zone Assignment Strategies in Mobile Fulfillment Systems[J]. Transportation Research Part E: Logistics and Transportation Review, 2019, 122: 119-142.

[5] VAN DEN BERG J P, ZIJM W H M. Models for Warehouse Management: Classification and Examples[J]. International Journal of Production Economics, 1999, 59(1/2/3): 519-528.

[6] 徐翔斌, 马中强. 基于移动机器人的拣货系统研究进展[J]. 自动化学报, 2022, 48(1): 1-20.

XU Xiang-bin, MA Zhong-qiang. Robotic Mobile Fulfillment Systems: State-of-the-Art and Prospects[J]. Acta Automatica Sinica, 2022, 48(1): 1-20.

[7] YANG Xi-ying, HUA Guo-wei, HU Lin-yuan, et al. Joint Optimization of Order Sequencing and Rack Scheduling in the Robotic Mobile Fulfilment System[J]. Computers & Operations Research, 2021, 135: 105467.

[8] LI Hong-li, ZHU Hong-rui, XU Dong-ming, et al. Dynamic Task Allocation Based on Auction in Robotic Mobile Fulfilment System[J]. Journal of Industrial and Management Optimization, 2023, 19(10): 7600-7615.

[9] MURILLO M, SÁNCHEZ G, GENZELIS L, et al. A Real-Time Path-Planning Algorithm Based on Receding Horizon Techniques[J]. Journal of Intelligent & Robotic Systems, 2018, 91(3): 445-457.

[10] 李昆鹏, 刘腾博, 贺冰倩, 等. “货到人”拣选系统中AGV路径规划与调度研究[J]. 中国管理科学, 2022, 30(4): 240-251.

LI Kun-peng, LIU Teng-bo, HE Bing-qian, et al. A Study on Routing and Scheduling of Automated Guided Vehicle in "Cargo-to-Picker" System[J]. Chinese Journal of Management Science, 2022, 30(4): 240-251.

[11] 窦佳佳. 强化学习及其在智能仓储中的应用研究[D]. 南京: 南京大学, 2016: 14-33.

DOU Jia-jia. Research on Reinforcement Learning and Its Application in Intelligent Warehousing[D]. Nanjing: Nanjing University, 2016: 14-33.

[12] 杨文华. 我国仓储物流机器人发展现状与未来趋势[J]. 物流技术与应用, 2017, 22(9): 100-102.

YANG Wen-hua. Development Status and Future Trend of Warehousing and Logistics Robots in China[J]. Logistics & Material Handling, 2017, 22(9): 100-102.

[13] 李晓旭, 马兴录, 王先鹏. 移动机器人路径规划算法综述[J]. 计算机测量与控制, 2022, 30(7): 9-19.

LI Xiao-xu, MA Xing-lu, WANG Xian-peng. A Survey of Path Planning Algorithms for Mobile Robots[J]. Computer Measurement & Control, 2022, 30(7): 9-19.

[14] KARUR K, SHARMA N, DHARMATTI C, et al. A Survey of Path Planning Algorithms for Mobile Robots[J]. Vehicles, 2021, 3(3): 448-468.

[15] 刘生伟, 马钺, 孟树峰, 等. 改进A*算法的AGV路径规划[J]. 计算机应用, 2019, 39(S2): 41-44.

LIU Sheng-wei, MA Yue, MENG Shu-feng, et al. Improved A*Algorithm for Path Planning of AGV[J]. Journal of Computer Applications, 2019, 39(S2): 41-44.

[16] DUCHOŇ F, BABINEC A, KAJAN M, et al. Path Planning with Modified a Star Algorithm for a Mobile Robot[J]. Procedia Engineering, 2014, 96: 59-69.

[17] 李伟光, 苏霞. 基于改进A*算法的AGV路径规划[J]. 现代制造工程, 2015(10): 33-36.

LI Wei-guang, SU Xia. AGV Path Planning Based on Improved A*Algorithm[J]. Modern Manufacturing Engineering, 2015(10): 33-36.

[18] SINGH Y, SHARMA S, SUTTON R, et al. A Constrained A*Approach towards Optimal Path Planning for an Unmanned Surface Vehicle in a Maritime Environment Containing Dynamic Obstacles and Ocean Currents[J]. Ocean Engineering, 2018, 169: 187-201.

[19] 牟德君, 初鹏祥. 基于改进A*算法的仓储环境AGV路径规划[J]. 自动化与仪表, 2022, 37(4): 40-45.

MU De-jun, CHU Peng-xiang. AGV Path Planning for Warehouse Environment Based on Improved A*Algorithm[J]. Automation & Instrumentation, 2022, 37(4): 40-45.

[20] REN Gong-chang, LIU Peng, HE Zhou. A Global Path Planning Algorithm Based on the Feature Map[J]. IET Cyber-Systems and Robotics, 2022, 4(1): 15-24.

[21] ZHONG Xun-yu, TIAN Jun, HU Huo-sheng, et al. Hybrid Path Planning Based on Safe A*Algorithm and Adaptive Window Approach for Mobile Robot in Large-Scale Dynamic Environment[J]. Journal of Intelligent & Robotic Systems, 2020, 99(1): 65-77.

[22] WANG Li-hui, LIU Ming-jie. Path Tracking Control for Autonomous Harvesting Robots Based on Improved Double Arc Path Planning Algorithm[J]. Journal of Intelligent & Robotic Systems, 2020, 100(3): 899-909.

[23] WANG Jian-kun, CHI Wen-zheng, LI Chen-ming, et al. Neural RRT*: Learning-Based Optimal Path Planning[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(4): 1748-1758.

[24] BOLU A-li, KORÇAK Ö. Path Planning for Multiple Mobile Robots in Smart Warehouse[C]// 2019 7th International Conference on Control, Mechatronics and Automation (ICCMA) Delft, Netherlands IEEE, 2020: 144-150.

Multi-AGV Path Planning Considering Conflict Avoidance

YANG Wei, YANG Si-yao,ZHANG Zi-han

(School of Mechanical and Electrical Engineering, Shaanxi University of Science and Technology, Xi'an 710021, China)

The work aims to improve the efficiency of the "goods to people" picking system in logistics enterprises during actual production, avoid conflict deadlock between automatic guided vehicles (AGVs), and study the conflict free path planning and collaborative obstacle avoidance problem of large-scale multi AGVs. Firstly, A*algorithm was improved considering the empty load, load situation, and path expansion cost of AGV, the cost function was adjusted dynamically and the path expansion method was optimized. Then, a conflict detection and avoidance algorithm was proposed, which scheduled path intersections that might generate local conflicts. Local conflict detection was achieved through reserved lock grids, and priority obstacle avoidance strategies were developed to solve local conflicts and deadlocks generated on AGV dynamic driving paths, to achieve global conflict free path planning. Multiple scenarios with different task volumes and AGV scales were simulated. The experimental results showed that the improved A*algorithm considering conflict avoidance could effectively achieve dynamic path planning for multiple AGVs in scenarios with 100 tasks, 90 shelf units, and 7 picking stations. Compared to the traditional A*algorithm, the average picking time was optimized by 52.61%. This method can achieve dynamic path planning for multiple AGVs in large-scale scenarios, effectively avoiding local dynamic conflicts while paying less turning costs. This method can provide new ideas and theoretical basis for relevant enterprises to achieve collaborative scheduling of multiple AGVs.

"goods to people" picking systems; automated guided vehicles; improved A*algorithm; conflict detection and obstacle avoidance algorithm; dynamic path planning

TP24

A

1001-3563(2023)23-0181-10

10.19554/j.cnki.1001-3563.2023.23.022

2023-02-24

陕西省西安市未央区科技计划（202203）

责任编辑：彭颋