水介质O形圈密封阻力研究

魏李玉，廖瑶瑶，2 ，陶泽 ，陶志磊

(1.太原理工大学机械与运载工程学院，山西太原 030024；2.煤矿综采装备山西省重点实验室，山西太原 030024)

0 前言

随着现代社会对安全、绿色的意识不断提高，煤矿这一特殊的生产环境也面临挑战，其液压支护设备的传动介质不仅要有防燃、防爆性，还要求绿色环保和经济实惠。水价格低廉、资源丰富，燃阻性和安全性高，本身清洁及阻燃的特点能够很好地满足这种要求。但是水相对油来说，黏度低、润滑性差，接触表面存在更大的摩擦力，严重影响液压阀等液压元件的动态特性[1]。O形圈结构简单、安装方便、密封性能可靠，广泛用于多种密封结构[2]。因此，研究O形圈在水介质中的密封摩擦特性对液压技术的发展具有重要意义。

王军等人[3-4]研究了预压缩量和流体压力对密封性能的影响，结果表明：随着预压缩量的增大，接触压力和接触长度明显增大；随着流体压力增大，接触压力增大，接触长度变化较小。ZHOU等[5-6]分析了丁腈橡胶O形圈在静密封和微动密封时的性能参数，结果表明：静密封流体压力超过6 MPa，必须使用挡圈避免间隙倒角处的剪切失效。常凯[7]基于Archard摩擦磨损模型，分析了接触压力和摩擦热对O形圈摩擦磨损的影响。陈祺鑫等[8]研究了加载振幅、激励频率、孔隙度对O形金属密封圈疲劳磨损和疲劳寿命的影响。BHAUMIK等[9-11]研究了油液压力和活塞杆速度对密封圈的影响，结果表明：在恒定的密封油压下，摩擦力随活塞杆速度的增大而减小。朱启惠等[12]分析密封压力小于10 MPa时，油液压力、压缩率和橡胶材料对O形圈往复运动摩擦性能的影响规律。

综上所述，已有研究主要集中在预压缩量、流体压力等参数对O形圈密封特性的影响。学者们通过建立摩擦力数值分析模型，分析油液压力和往复速度等对摩擦力的影响，工作介质为油液或乳化液，水介质条件下O形圈摩擦特性的报道较少。本文作者利用ANSYS软件对O形圈进行有限元分析，进一步探究预压缩率和流体压力对密封特性的影响；通过对比摩擦力理论计算结果和实验结果，探究流体压力和往复速度对O形圈摩擦力与摩擦因数的影响，为O形圈在水介质条件下的密封结构设计和性能优化提供依据。

1 O形密封圈仿真

1.1 数学模型

由于密封结构、边界条件和压力载荷等因素关于中心轴对称，产生的应力、应变和位移也关于中心轴对称，因此将O形圈密封结构简化为二维轴对称结构[13]。图1所示为O形圈往复密封结构简图。

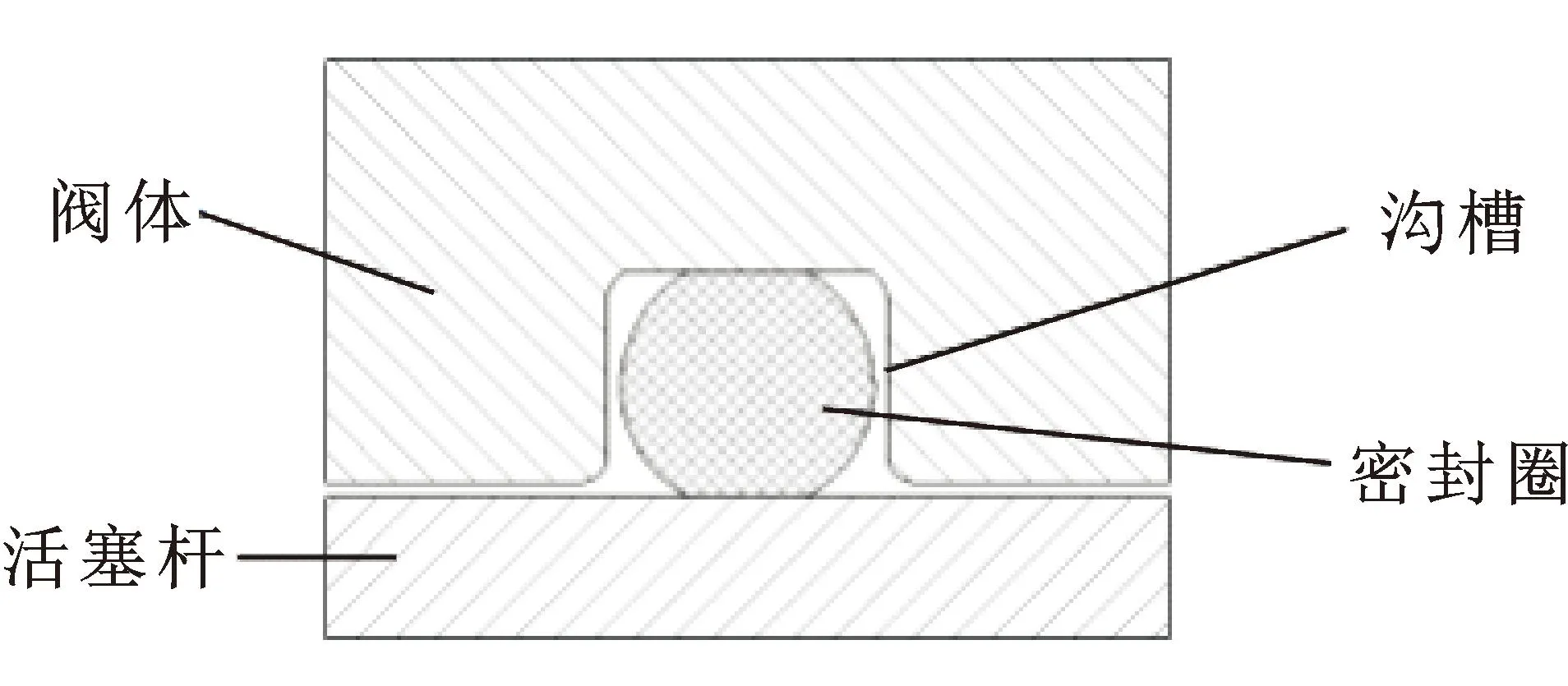
图1 O形圈往复密封结构简图

1.2 密封圈有限元模型

(1)材料定义

活塞杆和阀体材料为2Cr13，采用Linear Isotropic材料模型，弹性模量取200 GPa，泊松比取0.29。O形圈材料为丁腈橡胶，它是一种典型的近似不可压缩的超弹体，应力和应变之间表现为高度的几何非线性、材料非线性和状态非线性。选用两参数Mooney-Rivlin模型来模拟丁腈橡胶的力学行为[14-15]，应变能函数如下：

(1)

式中：W为应变能密度；I1和I2分别为第一和第二应力张量不变量；C10和C01为反映应力应变属性的材料常数；d和J是与弹性变形有关的参数。取材料参数：C10=1.87 MPa，C01=0.47 MPa，d=0.004 27。

O形圈的预压缩率w：

(2)

式中：d0为O形圈压缩前的截面直径；h为O形圈压缩后的截面高度。

(2)有限元模型及边界条件

图2所示为O形圈有限元模型。O形圈与活塞杆、沟槽底面和沟槽侧壁均存在接触，接触单元与目标单元分别采用CONTACT172和TARGE169，接触类型为面-面接触，接触算法采用增强拉格朗日算法，O形圈与活塞杆、沟槽底面和沟槽侧壁的摩擦因数均取0.13。活塞杆、阀体和O形圈均采用高阶二维八节点实体结构单元PLANE183，该单元类型能满足大应力、大变形的需求。在ANSYS软件中，载荷分2步施加：(1)固定沟槽所在的阀体，给活塞杆一个径向的位移模拟O形密封圈过盈安装产生的径向压缩；(2)在步骤(1)的基础上对O形圈与流体接触区域施加压力载荷模拟流体压力的轴向压缩，为确保压力载荷施加边界的准确性，流体压力的施加边界采取循环迭代逐点搜寻实现。

图2 O形密封圈有限元模型

(3)网格无关性验证

为了验证网格无关性，分析网格单元数目对计算结果的影响。分别划分4 016、15 756、62 447个网格单元进行计算分析。图3所示为5 MPa压力载荷下不同网格单元数目划分计算得到的O形圈von Mises应力云图，可以看出：4 016个网格单元计算得到的最大等效应力和15 756个网格单元计算得到的最大等效应力相差2.7%，存在较大的误差，15 756个网格单元和62 447个网格单元计算得到的最大等效应力仅差0.01%。随着网格单元数目的增加，计算时间从十多分钟陡增至数个小时，因而为了兼顾计算精度和计算时间，选择网格单元数为15 756的划分方法。

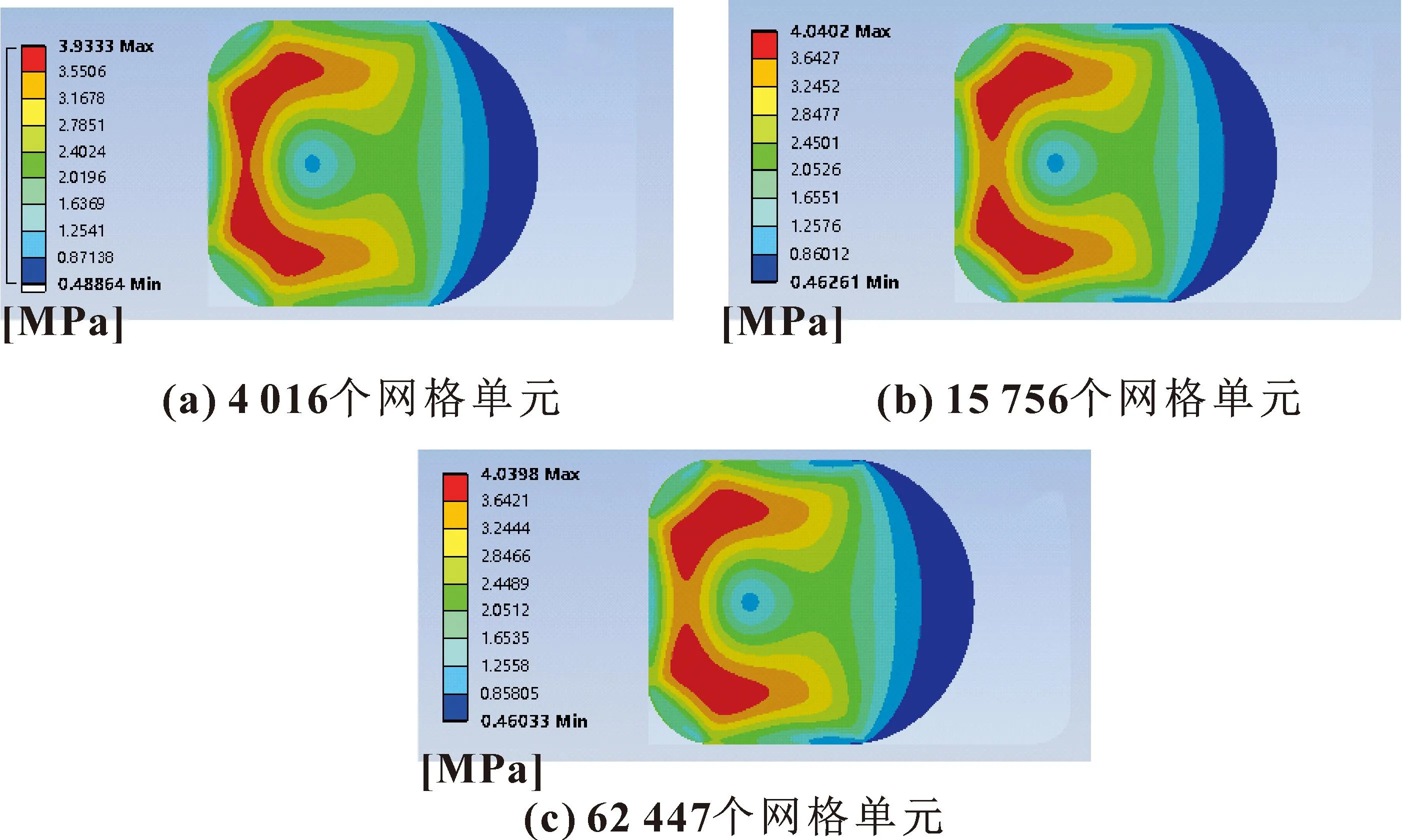
图3 不同网格单元数O形圈von Mises应力云图

2 有限元结果分析

2.1 预压缩率对密封性能的影响

图4所示为不同预压缩率时O形圈von Mises应力云图。可知：随着预压缩率的增大，von Mises应力也随之增大，von Mises应力集中区域逐渐由上下2个密封面向中间聚集和扩展。图5所示为预压缩率对接触长度和接触压力的影响。可知：随着预压缩率的增大，密封区域接触长度和接触压力明显增大，较长的接触长度表示较大的接触面积，密封效果会更好。因此，在预压缩率对其他因素影响相差不大时，可以适当选择较大的预压缩率，文中选择O形圈预压缩率为20%时进行研究。

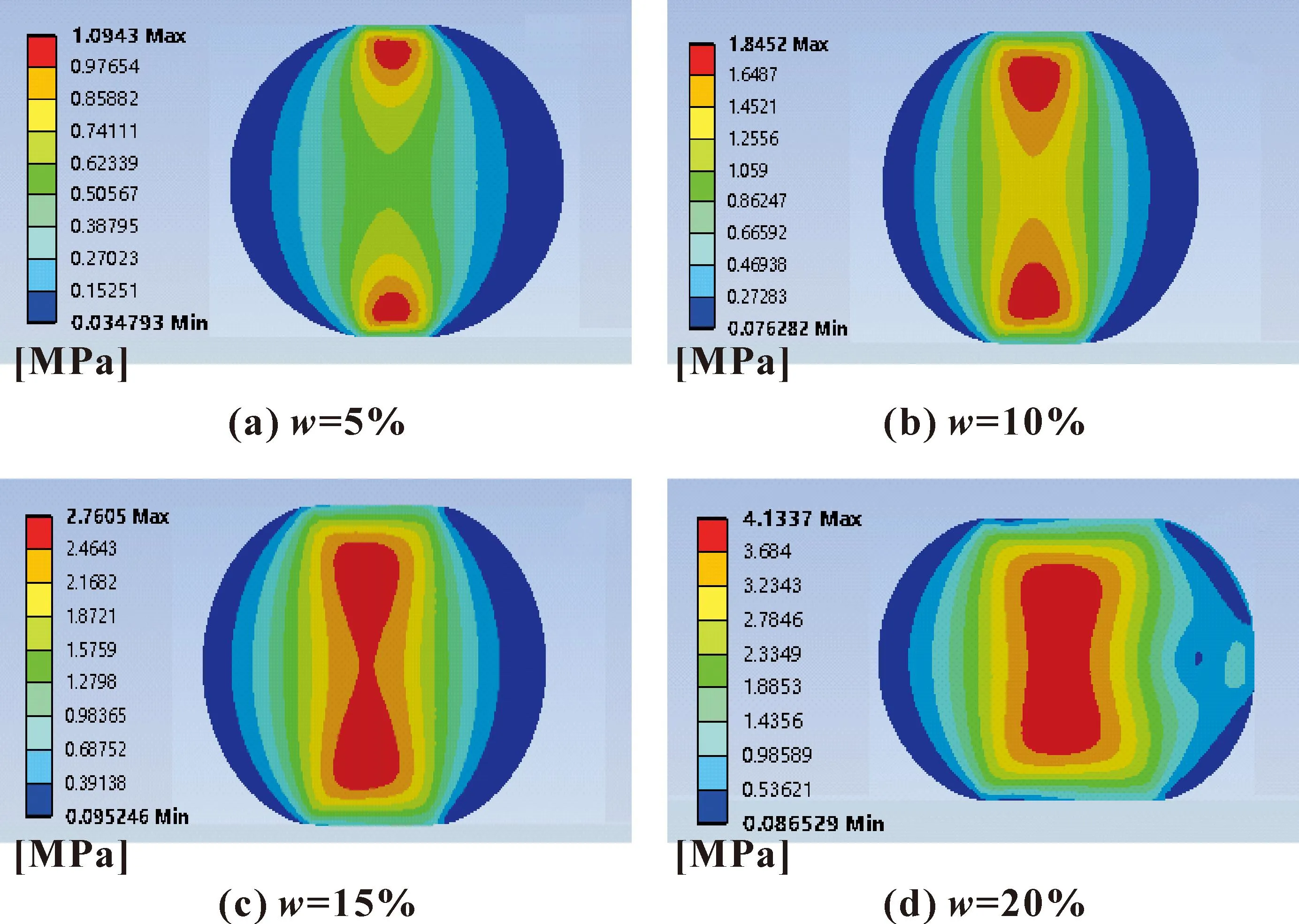
图4 不同预压缩率时O形圈von Mises应力云图

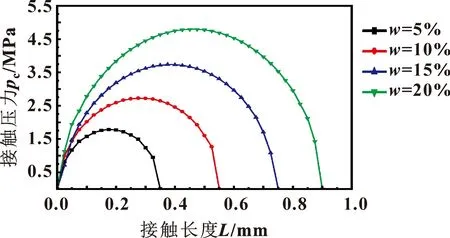
图5 预压缩量对接触长度和接触压力的影响

2.2 流体压力对密封性能的影响

图6所示为预压缩率w=20%、不同流体压力时O形圈von Mises应力云图。可知：随着流体压力的增大，最大von Mises应力增大，应力集中区域由高压流体侧向低压空气侧扩展。图7所示为预压缩率w=20%时，流体压力对接触压力和接触长度的影响。可知：O形圈与活塞杆接触区域的接触压力曲线趋势基本相同，接触压力随流体压力的增大表现为近似线性增大，接触长度随流体压力增大，当流体压力大于30 MPa时，接触长度减小，总体变化幅度较小。当流体压力从5 MPa增大到31.5 MPa时，密封面接触压力峰值从9.72 MPa增大到36.83 MPa，最大接触压力均大于流体压力，这表明O形圈从低压到高压都可以保证良好的自紧密封性。

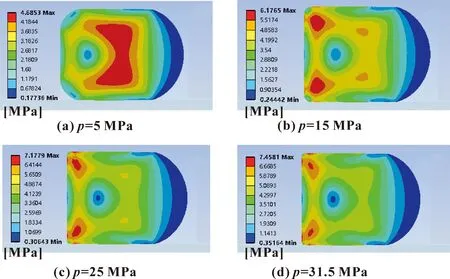
图6 不同流体压力时O形圈von Mises应力云图

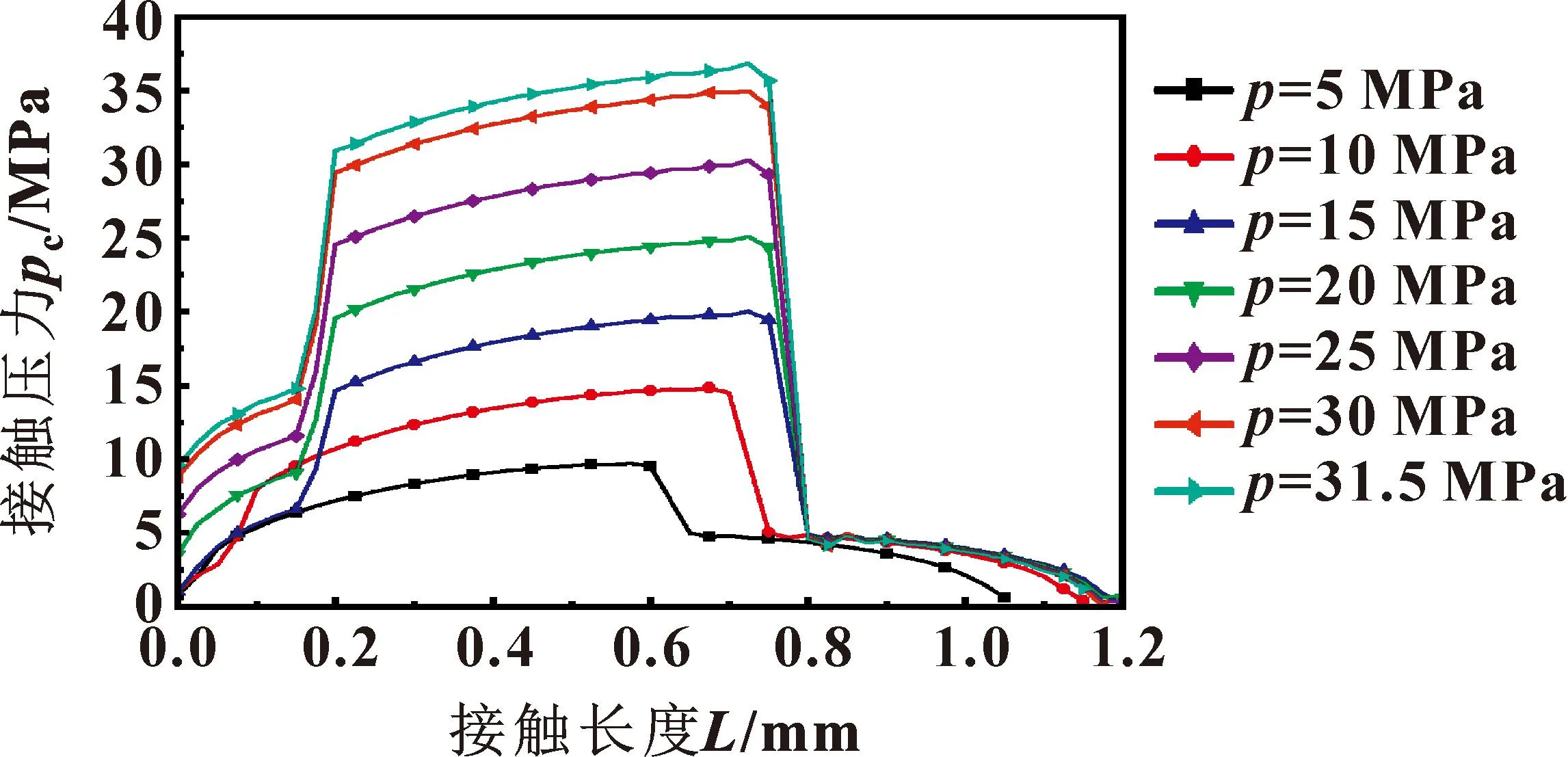
图7 流体压力对接触压力和接触长度的影响

3 摩擦特性分析

3.1 摩擦阻力计算

摩擦力对液压系统的动态响应有重要影响，过大的摩擦力往往会严重影响系统的稳定性和可靠性。在此通过不同方法计算O形圈的摩擦力。

微元法：通过ANSYS有限元软件求解接触面的应力分布，得到密封区域接触长度和接触压力，对接触压力进行数据拟合，得到接触压力的拟合方程，通过摩擦力计算公式[16]求解摩擦力：

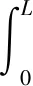
(3)

式中：D为活塞杆外径；L为密封圈密封区域接触长度；pL为密封圈密封区域接触应力分布函数；μ为密封圈与活塞杆的动摩擦因数。

经验法：通过O形密封圈摩擦力经验计算公式[17]进行计算：

F=μπΔpDb

(4)

式中：μ为密封圈与活塞杆的动摩擦因数；Δp为密封圈两侧压差；D为活塞杆外径；b为密封圈密封区域接触长度。

3.2 实验测量摩擦力

图8所示为液压往复密封实验装置。实验系统包括驱动单元、液压单元、测试单元和数据采集与分析单元4个部分。

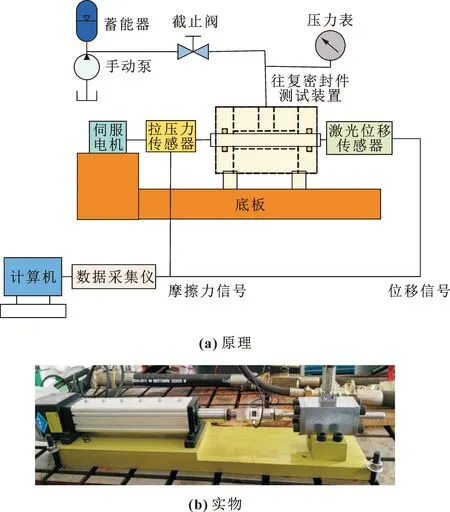
图8 液压往复密封实验装置

驱动单元的作用是为测试单元的活塞杆提供对中性好、运行平稳的往复运动速度，包括伺服电机、单片机和计算机。液压单元的作用是为测试单元提供压力稳定的工作介质，包括手动泵、蓄能器、截止阀和压力表。图8(b)为测试装置实物，测试单元的作用是提供封闭的测试腔，实现密封圈摩擦力测试。数据采集与分析单元的作用是将测得的数据信号通过数据采集仪实时传输到计算机作后续处理分析，包括拉压力传感器和激光位移传感器。LIAO等[18]设计的高水基比例阀工作压力为31.5 MPa，阀芯开启速度约为20 mm/s，通过实验对其摩擦力进行测试，图9为p=31.5 MPa、u=20 mm/s摩擦力实验曲线。

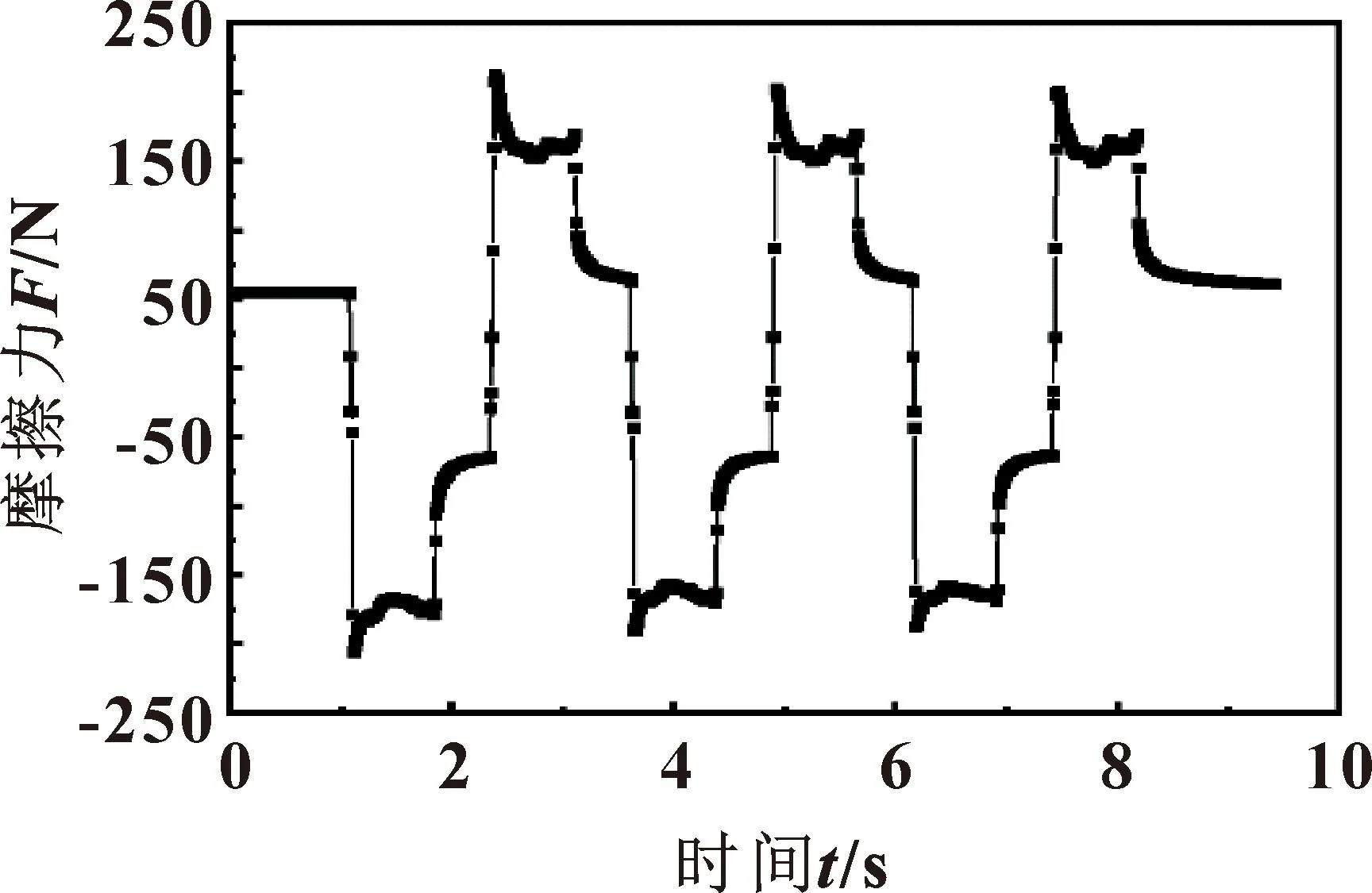
图9 p=31.5 MPa、u=20 mm/s摩擦力实验曲线

3.3 摩擦力结果对比

图10所示为不同方法得到的O形圈摩擦力变化曲线。可知：随着流体压力的增加，3种方法得到的摩擦力均在增大；流体压力超过12 MPa时，经验法计算得到的摩擦力比微元法和实验得到的大，随着流体压力的增大，其差值增大，最大误差分别为33.4%和33.06%。这是由于经验法采用的接触长度为定值，未考虑流体压力对接触长度的影响；微元法计算得到的摩擦力和实验得到的比较接近，最大误差为6.98%，可用于摩擦力的预估。

图10 不同方法得到的O形圈摩擦力变化曲线

3.4 摩擦力变化规律

图11所示为不同往复速度和流体压力O形圈摩擦力变化曲线。可知：相同速度，流体压力增大，摩擦力也增大，流体压力为10～20 MPa时，O形圈的摩擦力随流体压力变化较小；相同流体压力下，往复速度增大，摩擦力也增大，当往复速度大于20 mm/s时，O形圈摩擦力和往复速度呈近似线性关系。这是因为处于混合润滑状态的摩擦副，其摩擦力由流体剪应力和表面粗糙度之间的接触剪应力组成，由于水介质黏性小，液膜厚度较小，表面粗糙度之间的接触剪应力起主要作用，而表面粗糙度之间的接触剪应力与粗糙度之间的接触压力和往复速度近似呈正相关关系[10]。

图11 不同往复速度和流体压力O形圈摩擦力变化曲线

3.5 摩擦因数变化规律

图12所示分别为往复速度、流体压力对摩擦因数的影响曲线。由图12(a)可知：随着往复速度增大，干摩擦、湿摩擦和流体压力31.5 MPa时的摩擦因数均增大；往复速度为4～20 mm/s时，干摩擦摩擦因数随往复速度的变化明显，湿摩擦和流体压力31.5 MPa时的摩擦因数随往复速度的变化较小；相同往复速度，干摩擦的摩擦因数大于湿摩擦和流体压力31.5 MPa时的摩擦因数。这是由于干摩擦接触表面为直接接触，湿摩擦和流体压力31.5 MPa的接触表面之间存在液膜，减小了直接接触面积，因此干摩擦摩擦因数较大。相同往复速度，流体压力31.5 MPa的摩擦因数小于湿摩擦的摩擦因数，这是因为加载流体压力增大了接触面间的水膜厚度。由图12(b)可知：往复速度u=40 mm/s时，随着流体压力增大，摩擦因数先减小后增大。流体压力较小时，摩擦因数主要由材料剪切强度决定，摩擦因数较大；随着流体压力增大，接触表面微凸体发生变形，接触面积增大，摩擦因数受液膜影响较大，摩擦因数减小；流体压力继续增大，接触表面之间的液膜被破坏，摩擦因数开始增大。

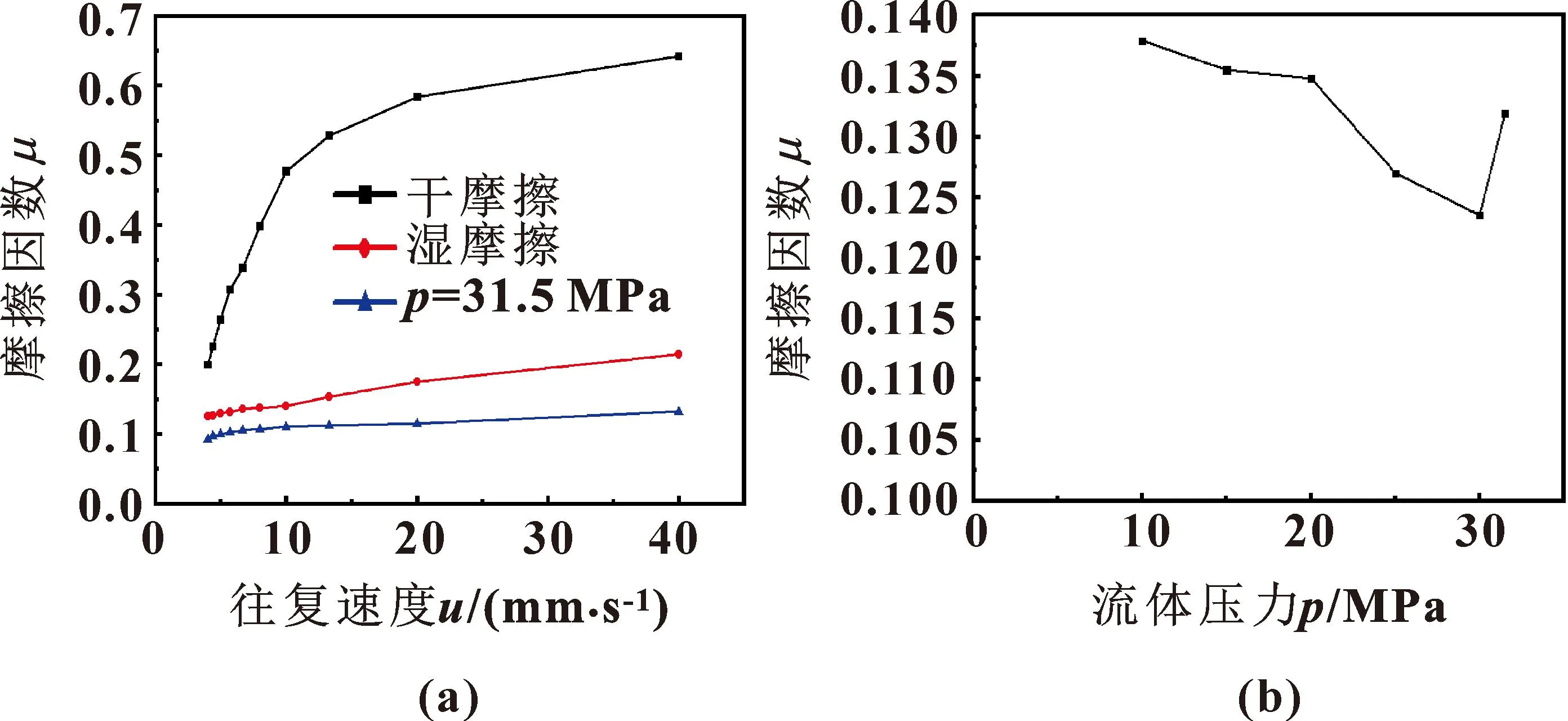
图12 往复速度(a)、流体压力(b)对摩擦因数的影响曲线

4 结论

(1)随着预压缩率的增大，von Mises应力也随之增大，最大von Mises应力与预压缩率近似呈线性关系。预压缩率增大，密封区域接触长度增大，适当选择较大的预压缩率有助于提升密封性能。

(2)随着流体压力的增大，O形圈最大von Mises应力增大，应力集中区域由高压流体侧向低压空气侧扩展。随着流体压力增大，接触压力近似线性增大，接触长度随之增大，流体压力大于30 MPa时，接触长度开始减小。

(3)微元法比经验法更加准确可靠，微元法得到的摩擦力和实验得到的比较接近，最大误差为6.98%，可用于摩擦力的预估。

(4)相同速度下，随着流体压力增大，摩擦力增大；相同流体压力下，随着往复速度增大，摩擦力也增大。

(5)随着往复速度增大，干摩擦、湿摩擦和流体压力31.5 MPa的摩擦因数均增大。相同往复速度，干摩擦的摩擦因数更大，这是由于干摩擦为直接接触，湿摩擦接触表面之间存在液膜，减小了直接接触面积。相同往复速度，流体压力31.5 MPa的摩擦因数小于湿摩擦的摩擦因数，这是因为加载流体压力增大了接触面间的水膜厚度。