基于有限时间扰动观测器的水厂加矾系统二阶滑模控制
王冬生,张 鹏,孙锦昊,郭若寒,蒋国平
(南京邮电大学自动化学院人工智能学院,江苏南京 210023)
1 引言
絮凝沉淀过程是水厂水质净化的重要环节,与出厂水水质安全密切相关.絮凝沉淀过程通过向原水中投加矾等絮凝剂去除原水中的悬浮杂质、胶体颗粒及附着于胶体颗粒上的细菌、病毒等有害物质.依据美国联邦环保局饮用水病毒去除技术标准,当滤后水浊度低于0.3 NTU时,病毒去除率高达99%[1].加强对水厂加矾系统的有效控制,严格限制沉淀池出水浊度,有利于出厂水水质稳定和实现高品质饮用水目标.
专家学者们对加矾系统控制问题进行了大量的研究和实践,提出了各种控制算法.流动电流法[2]和透光率脉动法[3]通过流动电流值和透光率检测跟踪絮凝沉淀过程状态,据此调整加矾量,但是由于流动电流值和透光率是间接反应絮凝沉淀过程的相对值,而且对仪器的灵敏度和维护要求较高,影响了在实际应用中的效果.直接将沉淀池出水浊度作为被控变量来控制加矾量是目前加矾系统控制的主流.由于历史数据中包含了控制过程中的所有信息,数据驱动方法[4]可以通过对历史数据的训练获得控制器参数,数据驱动方法避免了传统控制方法对过程模型的依赖,但是历史数据信息的获取往往是不全面的,一定程度限制了数据驱动方法在实际应用中的推广.虽然絮凝沉淀过程难以精确建模,但仍然可以通过采用高级反馈控制和扰动估计等方法,对其过程模型不精确,以及水质、水量突变等因素作用下的扰动进行抑制.
滑模控制(sliding mode control,SMC)是强非线性控制问题中的一种有效方法,具有抗扰动性强、动态响应快、控制实现简单等优势.目前,已有许多相关理论和应用研究[5–7].文献[5]针对一类非线性积分系统,利用有限时间控制技术,提出了一种输入饱和情况下的全局有限时间控制方案.文献[6]提出了一种新颖的二阶滑模(second-order sliding model,SOSM)控制方法来处理具有不匹配项的滑模动力学,从而减少控制通道中的项.文献[7]提出了一种带有有限时间扰动观测器(finite-time disturbance observer,FDOB)的连续动态滑模控制器.在实际应用中,SOSM控制使滑动变量的选择更加灵活,而且也更容易消除振颤问题.FDOB能够对扰动和过程不确定性进行估计,并通过前馈补偿设计减少对控制系统的不利影响.将扰动观测器与反馈控制相结合的复合控制方法是目前控制领域中抑制扰动和补偿模型不精确等问题的研究热点之一[8].
本文提出了一种基于FDOB和SOSM的水厂加矾系统复合控制方法,针对实际絮凝沉淀过程受原水水质和水量突变的影响,以及强非线性、不确定性和参数时变等问题,采用前馈补偿和反馈控制相结合的设计方法.仿真结果证明,在与实际絮凝沉淀过程相符合的模型不匹配和扰动情况下,本文提出的控制方法更好地实现了出水浊度的稳定.
2 系统描述与控制器设计
2.1 问题描述
自来水厂常规处理工艺流程如图1所示.其中,絮凝沉淀过程是在沉淀池入口处向原水中投加矾等絮凝剂,从而让各种杂质颗粒物等凝结成絮凝体,在重力作用下,絮凝体就能够沉淀在沉淀池底部,达到去浊澄清的目的.

图1 自来水厂常规处理工艺流程Fig.1 Conventional treatment process of waterworks
2.2 控制器设计
2.2.1 SOSM
针对上述问题,本文采用一种新的控制设计方法来处理具有不匹配不确定性的SOSM动力学.构造控制器包括3个步骤.首先,引入新的滑动变量,将传统SOSM动力学转变为具有不匹配不确定项的新型SOSM动力学.其次,通过定义失配不确定性的一些增长条件,以递归的方式构建一系列虚拟控制器来稳定新的滑动变量.最后,结合有限时间控制技术,设计一种带有非光滑项的SOSM控制器.
本文通过将出水浊度与设定值的偏差作为输入,设计二阶滑模控制器.其中G(s)为
由上式可得
其中:x∈Rn,代表出水浊度;u∈R,代表控制输入.现在将滑动变量s(即出水浊度误差)定义为s=xxref,其中xref表示浊度设定值.二阶滑模动力学方程为
其中:a(t,x)=-a1-a0x,b(t,x)=b,d(t)=ξω1(t)+ω2(t),此处ω1(t)为模型不匹配不确定项,ω2(t)为模型匹配扰动项,ω1(t)与ω2(t)及其一阶导数是有界的,因此存在一个正常数D>0使得|d(t)|≤D.
其中:U=v是一个虚拟控制器,A(t,x)=a(t,x)+ξω1(t)+ω2(t).在实际应用中,出水浊度x是有界的,这表示可以找到常数A0>0,使得|A(t,x)|≤A0.另外也存在正函数C(x)与正常数Km,使得|a(t,x)|≤C(x),b(t,x)≥Km.
为简化表达式,定义⎿x」α=sgnx|x|α,∀x∈R,∀m>0.设计控制器[9]
2.2.2 FDOB
FDOB是根据被控变量和控制变量对扰动进行估计的过程,将扰动估计作为前馈可以有效补偿扰动对被控过程的影响,从而达到抑制扰动的目的.给出的FDOB表示如下[10]:
其中:L1,L2和L3为正观测器增益,需要合理设计.然后,可以得到如下定理:
定理1[11]如果FDOB构造为式(6),则不确定项A(t,x)可以在有限时间内通过Z2准确估计,即可以找到一个时刻Tf>0使得z2≡A(t,x)对于∀t>Tf.
2.2.3 FDOB-SOSM复合控制设计
在FDOB和SOSM基础上设计复合控制方案,如图2所示.其中,FDOB采取主动抗扰动的策略对控制系统受到的外部扰动和模型不匹配进行估计进而抑制和消除.相较于只采用反馈控制,FDOB能更加有效地抑制干扰,极大地提高系统的鲁棒性.
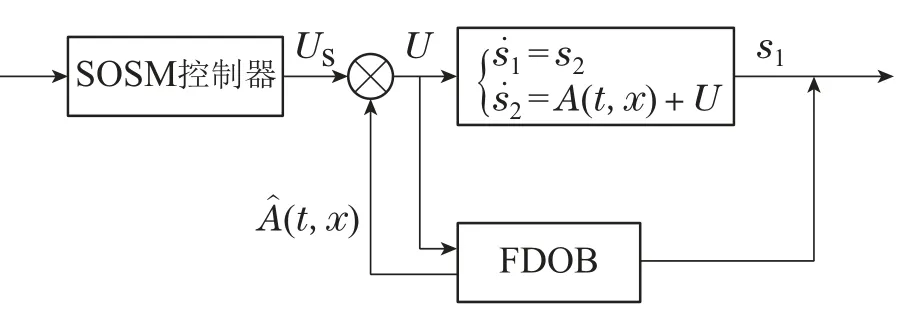
图2 复合控制方案框图Fig.2 Diagram of composite control scheme
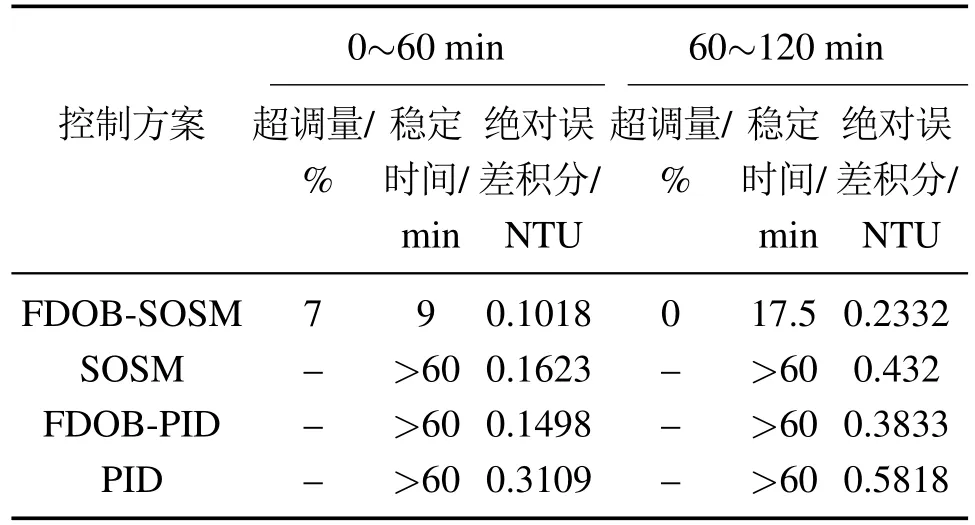
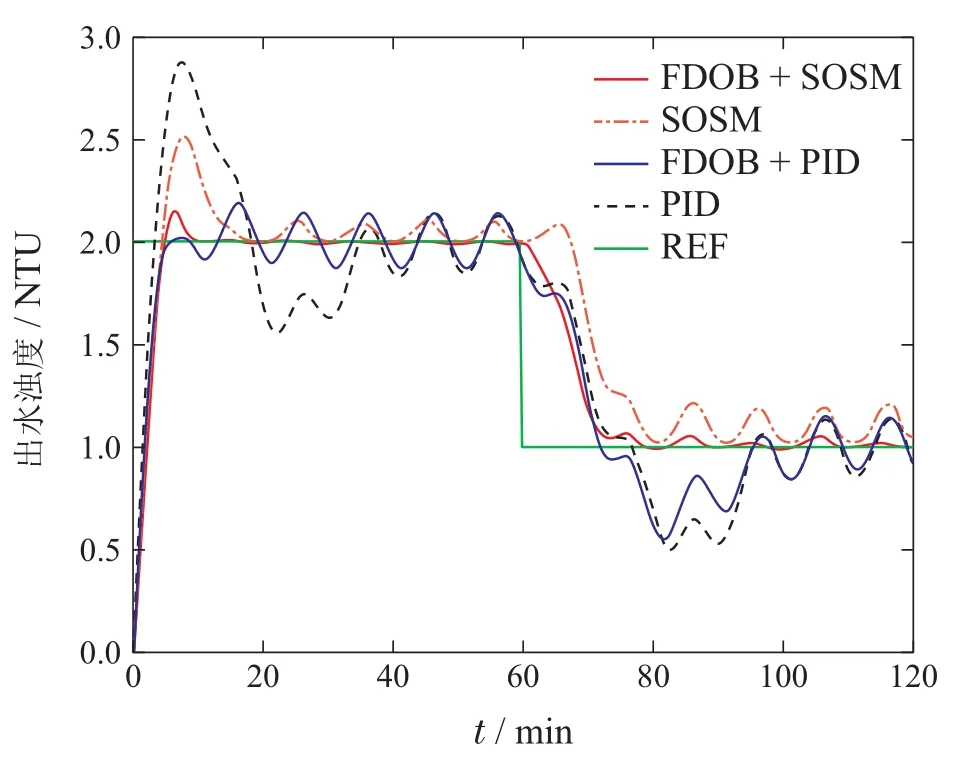
在滑模控制器设计中,令s1=s,s2=,滑模动力学可以改写为=s2,=A(t,x)+U,此刻需要注意的是不确定项A(t,x)通常是不可测量的,在实际应用中关于A(t,x)的精确值是未知的,这表示控制器(5)不会直接运用于系统(4)中,为此,假设A(t,x)是可微,并且满足|(t,x)| 假设1存在一个正常数Km,一个正函数C(x),使得|a(t,x)|≤C(x),|b(t,x)|>Km和r1=2,r2=r1-τ,r3=r2-τ且τ∈(0,1]. 定理2在假设1下,有一个常数a≥r1和正函数β1(s1),β2(s1,s2),建立闭环系统(4)–(5)的有限时间稳定性. 首先给出以下3个引理,然后给出定理2的证明. 引理1[12]如果0 引理2[13]如果a>0,b>0和实数c>0,那么有以下不等式: 引理3对于实数0 证分步骤证明定理2. 步骤1定义函数 且ρ≥a.然后鉴于假设1,V1(s1)沿SOSM动力学(4)的导数可以推导出为 步骤2定义函数 其中W2(s1,s2)可以设计为 V2(s1,s2)沿系统(4)的导数由下式给出: 使用引理2,可以从式(15)中计算出 同时,由引理1可以得知 通过式(9)可以得知 因为ξ0=0且使用引理3,还可以得出 通过将不等式(20)和系统(4)合并,使用引理2,可以得到两个正函数(s1)和(s1)使得 将不等式(21)代入(17),并使用引理2,可以计算出正增益(s1)使得 结合系统(4)得出 将不等式(16)(23)代入式(14)得到 根据不等式(24),可以设计 将控制器(25)代入式(24),结合V1(s1),可以验证出 然而,在实际应用中,无法使用FDOB准确估计系统不确定项,始终存在观测误差|(t,x)|=A(t,x)-z2.因此,可以找到一个时刻Tf和一个正常数ε,使得|(t,x)|≤ε,对于∀t≥Tf.最后,结合SOSM算法和FDOB技术得到的最后一个结果由定理3给出. 定理3在假设1下,有一个常数a≥r1和正函数β1(s1),β2(s1,s2)使得下面的SOSM控制律成立: 其中z2是FDOB(6)给出的不确定项A(t,x)的估计,建立闭环系统(4)–(5)的有限时间稳定性. 证根据U=v和v=b(t,x)u的定义,得到 将控制器(29)放入系统(4)中,可以得到 因为系统(30)与系统(4)结构相似,则系统(30)在控制器Us下将有限时间收敛到原点.由此进一步验证控制器不会在Tf之前发散到无穷大. 选择一个有限时间有限函数 由于系统(30)中的不确定项A(t,x)总是有界的,因此可以很容易地得到(t,x)=A(t,x)-z2也是有界的.因此,可以找到一个正常数Υ使得 之后可以得出结论 这意味着系统(30)的状态s1和s2在时间间隔(0,Tf]内是有界的.此外,可以得出结论,系统(30)可以通过复合控制器(28)在有限域内稳定到原点.因此,滑动变量s可以在有限时间内稳定为零.证毕. 加矾系统随着实际工况的变化而不同,本文采用在线辨识方法对加矾系统进行建模,即 本文在MATLAB环境下进行控制仿真.模拟在0∼60 min期间将出水浊度设定值保持在2 NTU,在60∼120 min期间将出水浊度设定值保持在1 NTU.选择超调量、调节时间(∆=0.02 min)和绝对误差积分(integral absolute error,IAE)作为量化指标来评估控制方案,即 其中:yr(t)是参考值,y(t)是实际过程输出. 为了设计加矾系统的二阶滑模控制器,首先要选择一个滑动变量.将滑动变量s(即浊度误差)定义为 式中:y表示出水浊度,yref表示出水浊度设定值,得到滑动变量s的动力学方程 在加矾系统中,由于天气恶劣或水源受到污染,原水水质有时会发生突变.这导致沉淀池的原水水质超出正常范围,并且建立的模型过程与实际过程不匹配.为了证实所提出的控制方案的鲁棒性,在模型不匹配的情况下,K和T提高20%,从而得到了传递函数 因此,滑动变量s的动力学方程 为了更好展示FDOB-SOSM复合控制器的性能,仿真中将工业系统中广泛运用的比例–积分–微分(proportional integral derivative,PID)控制器,SOSM控制器,FDOB-PID复合控制器加入对照实验中,仿真结果如图3和表1所示.由图3可以看出在0∼60 min和60∼120 min,本文提出的FDOB-SOSM复合控制,能够更好地跟踪出水浊度设定值(reference,REF)的变化;由表1可知FDOB-SOSM复合控制下的系统稳定时间最少,绝对误差积分最小,整体性能要优于其他控制器. 表1 模型不匹配情况控制性能指标Table 1 Control performance index of model mismatch 图3 模型不匹配情况仿真结果Fig.3 Simulation results of model mismatch 在加矾系统中,由于原水水质和水量变化、以及传感器信号波动等原因会导致对加矾系统产生一定的扰动.因此考虑受扰动情况,由传递函数(36),得到滑动变量s的动力学方程 式中d(t)为扰动,仿真中取的是幅度0.05,频率为0.1的正弦信号.控制器采用式(42). 仿真结果如图4和表2所示.由图4可以看出在0∼60 min,只有FDOB-SOSM控制方案很好的跟踪设定值.可以看出基于FDOB的扰动估计补偿,使FDOBSOSM复合控制具有更好的抗扰动能力;同时,由表2可知FDOB-SOSM复合控制下的系统稳定时间最少,绝对误差积分也最小. 表2 受扰动情况控制性能指标Table 2 Control performance index under disturbance 图4 受扰动情况仿真结果Fig.4 Simulation results under disturbance 为了进一步对比FDOB-SOSM控制方案的性能,在模型不匹配且同时遭受扰动的情况下,由传递函数(40),得到滑动变量s的动力学方程 式中d(t)为扰动,仿真中取的是幅度0.05,频率为0.1的正弦信号,控制器采用式(42). 仿真结果如图5和表3所示.由图5可以看出在0∼60 min和60∼120 min,只有FDOB-SOSM控制方案很好的跟踪设定值.可以看出模型不匹配和外部扰动时,基于FDOB的扰动估计补偿,使FDOB-SOSM复合控制具有更好的设定值跟踪和抗扰动能力.由表3可知,FDOB-SOSM控制方案具有更好的鲁棒性、更快的响应和更小的超调. 表3 模型不匹配受扰动情况控制性能指标Table 3 Control performance index of model mismatch under disturbance 图5 模型不匹配受扰动情况仿真结果Fig.5 Simulation results of model mismatch under disturbance 本文提出了一种水厂加矾系统的FDOB-SOSM复合控制方案,采用了一种改进的带有非光滑项的SOSM控制方法实现加矾反馈控制;FDOB用于估计模型不匹配和扰动,并应用估计值作为前馈补偿削弱模型不匹配和扰动带来的不利影响.采用李亚普诺夫函数证明了系统的稳定性.在实际工程中存在的水质、水量突变等影响下造成的模型不匹配与扰动分别进行了仿真.仿真结果证明了控制方法的有效性.3 系统稳定性分析
4 仿真验证
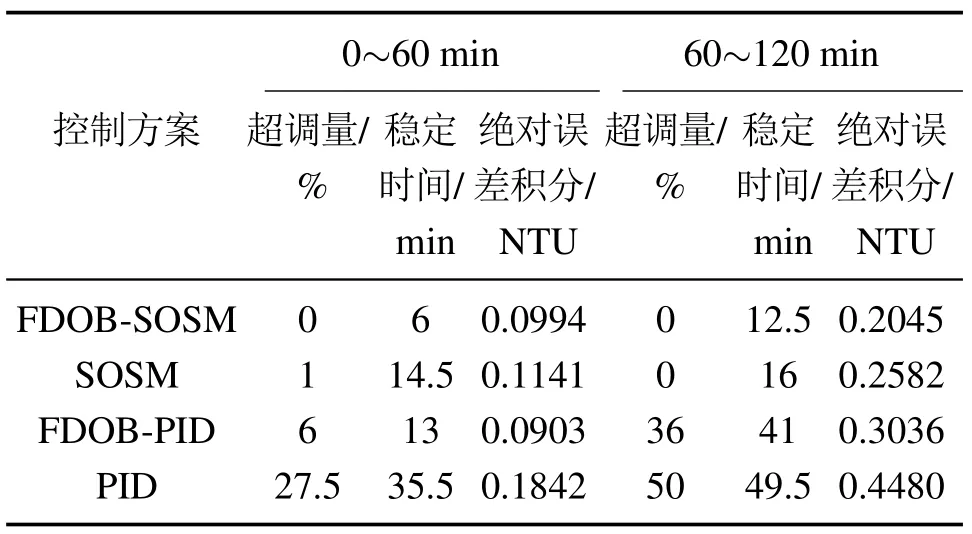
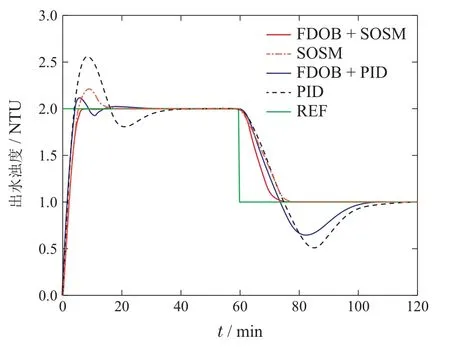
4.1 模型不匹配情况
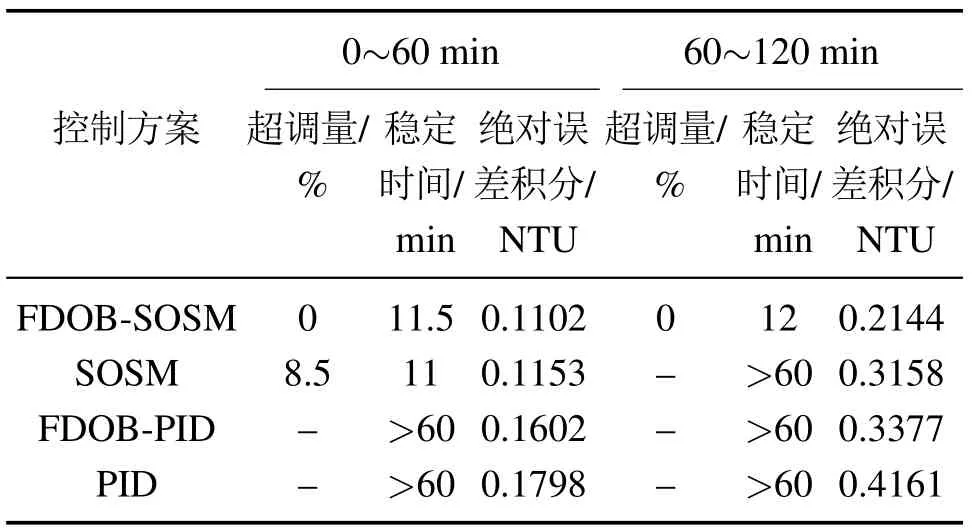
4.2 受扰动情况
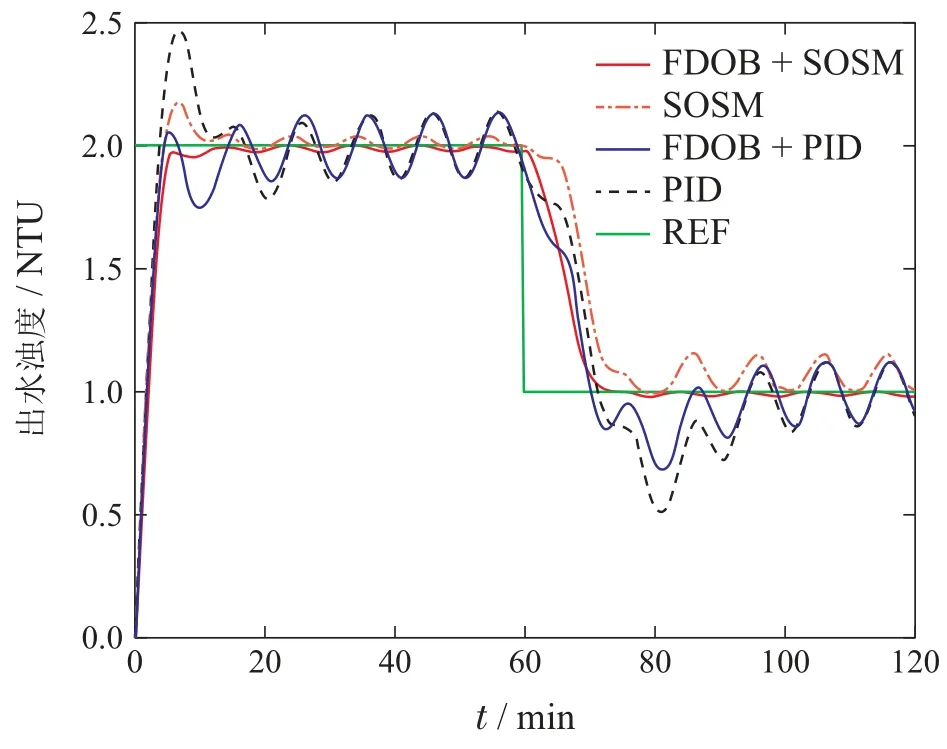
4.3 模型不匹配受扰动情况
5 结论

